三維空間液滴運動模型數值解法研究

張 璜，薄涵亮

(清華大學 核能與新能源技術研究院，北京 100084)

液滴運動現象廣泛存在于各種核能動力裝置中。例如，蒸汽發生器內的汽水分離裝置中就存在大量液滴運動。汽水分離裝置的作用是將蒸汽發生器產生的濕蒸汽流進行干燥。歐美各國規定經汽水分離器干燥后的蒸汽濕度要小于0.25%，否則高速蒸汽流夾帶著這些液滴會造成二回路管道、關閉件腐蝕，以及汽輪機的汽蝕，影響汽輪機壽命。因此，汽水分離裝置的分離效率關系到核電系統運行的經濟性和安全性。

常見的汽水分離裝置有旋葉式分離器、重力式分離器和波形板式分離器，它們內部的液滴在蒸汽場中運動，流出或被分離器捕獲。通過建立汽水分離器內液滴運動模型并對其進行求解，可得到液滴在分離器內部的運動軌跡和數目分布，進而能較為細致地研究分離器對液滴的分離機理，從而為設計高性能的汽水分離器提供理論依據。

不同學者采用的液滴運動模型雖不同，但該模型均可表述為1組一階常微分方程。由于該組常微分方程通常無解析解，所以一般采用數值方法對其進行求解。龐鳳閣等[1]采用高階方程的Runge-Kutta(RK)算法對波形板內的液滴運動模型進行求解，得到了直徑為7～10 μm的液滴運動軌跡。陳韶華等[2-3]采用定(單)步長的RK算法求解液滴運動模型，對重力分離空間內直徑為0～350 μm的液滴和波形板分離器內直徑為10.5～12.5 μm的液滴的運動行為均作了研究。王曉墨等[4]采用向前Euler算法求解液滴運動模型，得到了直徑為10、20和900 μm的液滴在波形板內的運動軌跡。張謹奕等[5-6]考慮了液滴在三維空間中受到的Magnus升力和Saffman升力，采用4級4階顯式單步長RK算法對該模型進行數值求解，但只對波形板汽水分離器內直徑大于50 μm的液滴的運動軌跡和分離效率進行了研究。

向前Euler算法雖易編程實施，但它是顯式算法且僅有一階精度，穩定性和精度均不能保證[7]。單步長RK算法雖能保證數值求解結果具有較高精度，但它依然是顯式算法，數值穩定性不夠好[7]。

針對以上不足，本文擬提出三維空間內液滴運動模型數值求解的一種算法，即算子分裂算法(OS算法)。本文首先簡述適用于三維空間的液滴運動模型，隨后詳細介紹OS算法的數值離散格式，最后分別采用RK算法和OS算法對波形板汽水分離器內的液滴運動模型進行求解，從相容性、穩定性、計算精度和計算效率等方面對這兩種算法進行比較。

1 三維空間液滴運動模型的數學表述

在三維空間中的單個液滴，不僅有相對于固定坐標系的平動，還有繞自身對稱軸的轉動和液滴表面的變形運動。在上述運動的同時，除了受到流場的作用力，還可能會對流場的變化產生影響。

因此，考慮到三維空間液滴運動的復雜性，本文提出如下假設：

1) 液滴和流場間無質量和熱量交換；

2) 液滴為剛性圓球，在運動過程中不發生形變，因此液滴可看作剛體，其運動可分解為平動和轉動；

3) 流場對液滴有作用力，而液滴在運動過程中對流場無影響。

基于以上假設，液滴的轉動方程為：

(1)

液滴運動方程為：

(2)

其中：md=πρdd3/6，ρd為液滴密度；vd為液滴速度；液滴所受曵力FD=πCDρf|vf-vd|(vf-vd)d2/8，CD為曵力系數；液滴所受慣性質量力FA=πρfd3[d(vf-vd)/dt]/12；液滴所受體積力FV=πd3(ρd-ρf)g/6，g為重力加速度；液滴所受Magnus升力FM=πCMaρfd3(vf-vd)×(ωd-ωf/2)/8，CMa為Magnus升力系數；液滴所受Saffman升力FS=1.615CSa(Rμ)2(ρfμf)0.5d2×|ωf|-0.5[(vf-vd)×ωf]，CSa為Saffman升力系數，(Rμ)2表示液滴內部環流量對升力的影響，μf為流體動力黏性系數。

將以上各表達式代入式(1)和(2)，并將方程左邊系數歸一化得：

(3)

其中：λ1=-15ρf/16π、λ2=3ρf/(4ρdd+2ρfd)、λ3=3ρf/(4ρd+2ρf)、λ4=[1.615(μd+2μf/3)2/(μd+μf)2(μfρf)0.5]/(ρdπd/6+ρfπd/12)、λ5=2(ρd-ρf)/(2ρd+ρf)為歸一化系數；CM、CD、CMa、CSa等系數的值詳見文獻[5]。

式(3)即為本文需求解的三維空間液滴運動模型的數學表述式。

2 OS算法的離散格式

算子LA為：

(4)

算子LB為：

(5)

LA求解液滴的角速度變化和由曵力加速度引起的液滴速度變化；LB求解由Magnus升力、Saffman升力加速度和體積力加速度引起的液滴速度變化。這樣就將求解式(3)的過程轉換成分別求解式(4)和(5)，這一步稱為算子分裂。

假設時間步長τ=ti+1-ti，將(ωd，vd)記為Yd，從時刻ti到時刻ti+1，OS算法實施步驟為：

Yi+1=LAi(τ/2)LBi(τ)LAi(τ/2)·Yi

(6)

其中，LAi和LBi為離散的LA和LB算子。

OS算法需將式(6)表示的過程對時間離散。本文采用隱式算法求解算子LA，選取具有二階精度的隱式梯形算法[7]離散式(4)：

(7)

同時采用RK算法離散式(5)，得：

(8)

引入定義：

(9)

那么，K1、K2、K3、K4為：

(10)

OS算法針對式(3)的離散格式為式(7)和(8)，對每一個時間步長的計算步驟為式(6)。

3 OS算法的驗證

本文將RK算法[5]也用于求解式(3)，以模擬直徑為1～50 μm的液滴在波形板中的運動軌跡，從兩種算法的相容性、穩定性、計算精度和計算效率等方面來驗證OS算法的性能。

本算例中，采用無鉤型波形板[1]，其幾何形狀示于圖1a。波形板的波數為2，入口及出口端長度均為L=10 mm，波形板間距H=12.5 mm，曲折角α=45°，折邊B=25 mm，并定義w=B/H。假設波形板在冷態工況下工作，用不可壓縮空氣代替蒸汽[1]，其密度ρf=1.225 kg/m3，動力黏性系數μf=1.789 4×10-5Pa·s；液滴密度ρd=998 kg/m3，動力黏性系數μd=9.98×10-4Pa·s。波形板內液滴和氣體的運動可簡化為二維，所以可忽略液滴受到的體積力，可令式(3)中λ5=0。

波形板內氣體的二維流動滿足Navier-Stokes方程，其連續性方程和動量守恒方程為：

(11)

(12)

其中，υf=μf/ρf為流體運動黏性系數。利用FLUENT 6.3.26對波形板內氣相流場進行模擬，流動設置為穩態，入口速度分別設為3、5和7 m/s，黏性模式選用標準κ-ε湍流模型，固壁設置為無滑移邊界，出口設置為充分發展流動，選用SIMPLE算法求解，各項殘差設置為10-4 [8]。當入口速度為3 m/s時，計算結果采用Tecplot處理得到的波形板內流場的流線示于圖1b。

為了模擬液滴在波形板內流場中的運動軌跡，需將FLUENT 6.3.26計算所得的流場速度和速度梯度保存為輸出文件，作為求解液滴運動模型的已知流場速度和旋度。

3.1 OS算法相容性分析

隱式梯形法的局部截斷誤差為o(τ2)[7]，RK算法的局部截斷誤差為o(τ5)[7]。

采用隱式梯形法和RK算法構造的OS算法的局部截斷誤差階數推導過程為：采用OS算法求解式(3)，當計算到第i步時，液滴的角速度和速度可寫為yi=(ωdi，vdi)，采用OS算法計算得到第i+1步的數值解為：

yi+1=[(yieLAτ/2+o(τ2))eLBτ+

o(τ5)]eLAτ/2+o(τ2)

(13)

利用式(3)得到第i+1步的精確解為：

(14)

式(14)減去式(13)所得結果即為OS算法的局部截斷誤差，最終有：

ο(τ2)

(15)

由式(15)可知，OS算法構造的離散格式的局部截斷誤差為o(τ2)，與式(3)相容。

3.2 OS算法穩定性分析和RK算法時間步長比較

提出一個算法，首先必須保證它構造的離散格式和原方程相容。除此之外，更重要的是保證算法的收斂性。證明算法的收斂性往往非常困難[9]，但只要對實際問題建立合適的物理與數學模型，則假定由相容與穩定的離散格式就能獲得收斂的數值解[10]。

由于所求解的式(3)為非線性常微分方程組，因此本文僅討論RK算法和OS算法的局部初值穩定性。在本文計算的波形板流場中，直徑小于50 μm的液滴的平動雷諾數Red(Red=ρf|vf-vd|d/μf)和轉動雷諾數Reω(Reω=ρf|ωd-ωf/2|d2/4μf)總體上分別小于6.2和1，且隨著直徑的減小，Red和Reω更加趨近于滿足上述要求。此時可取CM=16π/Reω、CD=24/Red、CMa=1、CSa=1，在二維情況下，式(3)變為：

(16)

其中：α=4μf/d2；β=36μf/(2ρd+ρf)d2；γ=2ρf/(4ρd+2ρf)；η=19.38(μfρf)0.5/πd(2ρd+ρf)。本文提出的OS算法主要針對直徑小于50 μm的液滴，所以比較RK算法和OS算法穩定性時，可直接針對式(16)進行分析。

式(16)的系數矩陣Gcreep為：

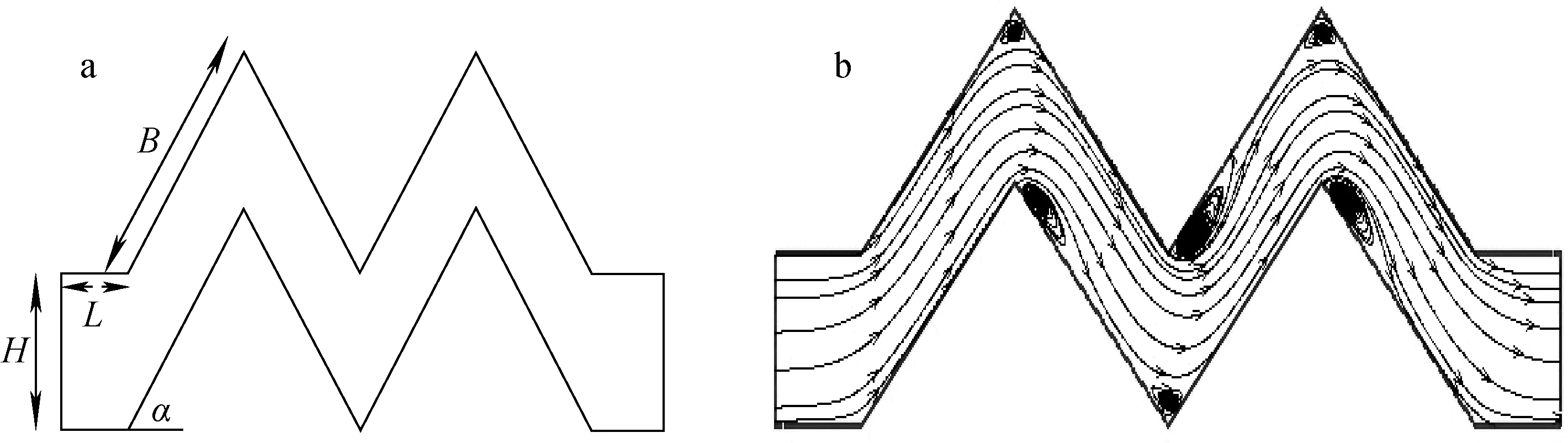
圖1 波形板的幾何形狀(a)和內部流場流線(b)

(17)

其中：ωd=(0，0，ωd)；ωf=(0，0，ωf)；vd=(vdx，vdy，0)；vf=(vfx，vfy，0)。系數矩陣Gcreep包含要求解的未知數ωd、vdx和vdy，采用量綱分析估計Gcreep的大小。本文中，液滴速度和流場速度的量級為10 m/s，液滴角速度的量級為102rad/s，流場旋度的量級為103rad/s，液滴直徑的量級為10-5m，結合已給出的液滴和流場的物性參數，系數矩陣Gcreep約為：

(18)

Gcreep特征值的實部為ζ1=-1.08×107、ζ2=ζ3=-3.24×103，可見式(16)是剛性方程。

用RK算法求解式(3)時，根據絕對穩定性條件[11]理論預測出計算不同直徑液滴所需的最大時間步長τmaxTRK=-2.78/ζmin，ζmin為系數矩陣Gcreep的最小特征值(若特征值為復數，取特征值的實部)。通過數值實驗，得到不同直徑液滴情況下保持RK算法穩定的最大時間步長τmaxNRK，將兩者同時列于表1。由表1可見，理論值和數值實驗值很吻合。

OS算法的實施過程見式(6)，ti+1時刻，yi+1=LAi(τ/2)LBi(τ)LAi(τ/2)·yi，令GOS=LAi(τ/2)LBi(τ)LAi(τ/2)，則GOS的具體表達式為：

(19)

其中，χ=γ(ωf/2-ωd)-ηωf/|ωf|0.5。GOS的特征值ζ1=(1+ατ/2)2/(1-ατ/2)2，ζ2=ζ3=(1-βτ/2)2(1-τ2χ2/2+τ2χ4/24)/(1+βτ/2)2，要使OS算法穩定，只需保證GOS特征值的實部的絕對值小于1。已知α<0，β>0，那么必有|ζ1|<1，|ζ2|=|ζ3|=((1-βτ/2)2/(1+βτ/2)2)|1-τ2χ2/2+τ2χ4/24|<|1-τ2χ2/2+τ2χ4/24|，因此只需滿足|1-τ2χ2/2+τ2χ4/24|<1就能保證OS算法穩定，其解為：

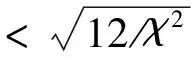
(20)

令τTOS=(12/χ2)0.5，不同液滴直徑下的τTOS列于表1。由表1可知，τTOS的量級為10-1～10-3，而τmaxTRK和τmaxNRK的量級為10-6～10-9。值得注意的是，τTOS僅是保證OS算法穩定的充分條件，所以使OS算法穩定的最大時間步長τmaxOS≥τTOS。通過數值實驗也發現，對于不同直徑的液滴，τmaxOS均可放寬到1 s，因此也證實了上述觀點。通過以上分析可知，OS算法可取的時間步長大于RK算法時間步長的取值，因此OS算法的穩定性優于RK算法。

3.3 OS算法計算精度和計算效率分析

由3.1節可知，RK算法的局部截斷誤差為o(τ5)，而OS算法的局部截斷誤差為o(τ2)，為保證OS算法依然具有較好的精度，對其時間步長選取如下：

(21)

RK算法的時間步長τRK取表1中給出的τmaxNRK，注意此時τOS仍比τRK大。

比較了兩種算法計算得出的不同直徑液滴在波形板內的軌跡形狀。兩種算法中，液滴進入波形板的速度和位置均相同。液滴進入波形板的速度與波形板內流場入口速度相等，液滴入射方向垂直于波形板入口，液滴初始位置在波形板入口處均勻分布。同一直徑的液滴計算10個。圖2為4種不同直徑液滴以不同初始速度在波形板內的運動軌跡示意圖。可見，兩種算法得到的軌跡形狀相似。

表1 τmaxTRK、τmaxNRK和τTOS的比較

記RK算法計算得到液滴恰好流出或被波形板捕獲的位置(終端位置)為(xRK，yRK)，OS算法得到液滴的終端位置為(xOS，yOS)。為了定量比較兩種算法所得液滴終端位置的精度，分別定義x軸和y軸終端位置的相對誤差為εx和εy：

(22)

兩種算法計算所得不同直徑液滴終端位置平均值及其相對誤差列于表2～4。由表2～4可看出，εx在0.6%以內，εy在2.7%以內，可見OS算法和RK算法精度相當。

在計算表2的同時，記錄每個液滴在波形板內經過完整軌跡所需的計算時間(取計算機的CPU耗時)并取平均值，定義RK算法計算單個液滴的平均CPU耗時除以OS算法的平均CPU耗時為CPU耗時倍數，最后所得結果列于表5。

由表5可見，3種工況的平均CPU耗時倍數均大于35。對于直徑相對較小的液滴，如1 μm液滴，CPU耗時倍數可達300以上。因此，表2～5結果可證實，在保證OS算法和RK算法精度相當的前提下，OS算法的計算效率優于RK算法。

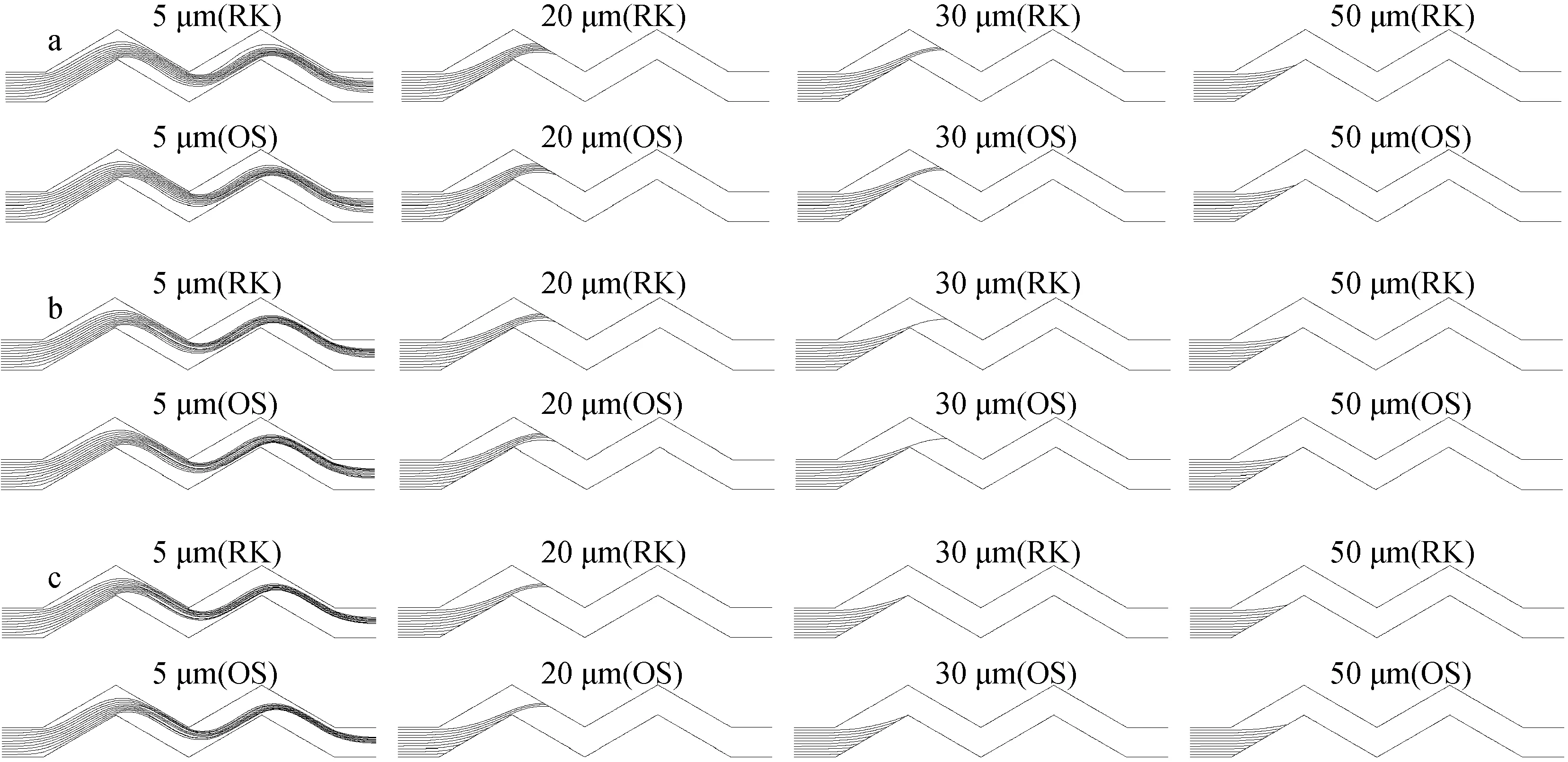
液滴初始速度：a——3 m/s；b——5 m/s；c——7 m/s

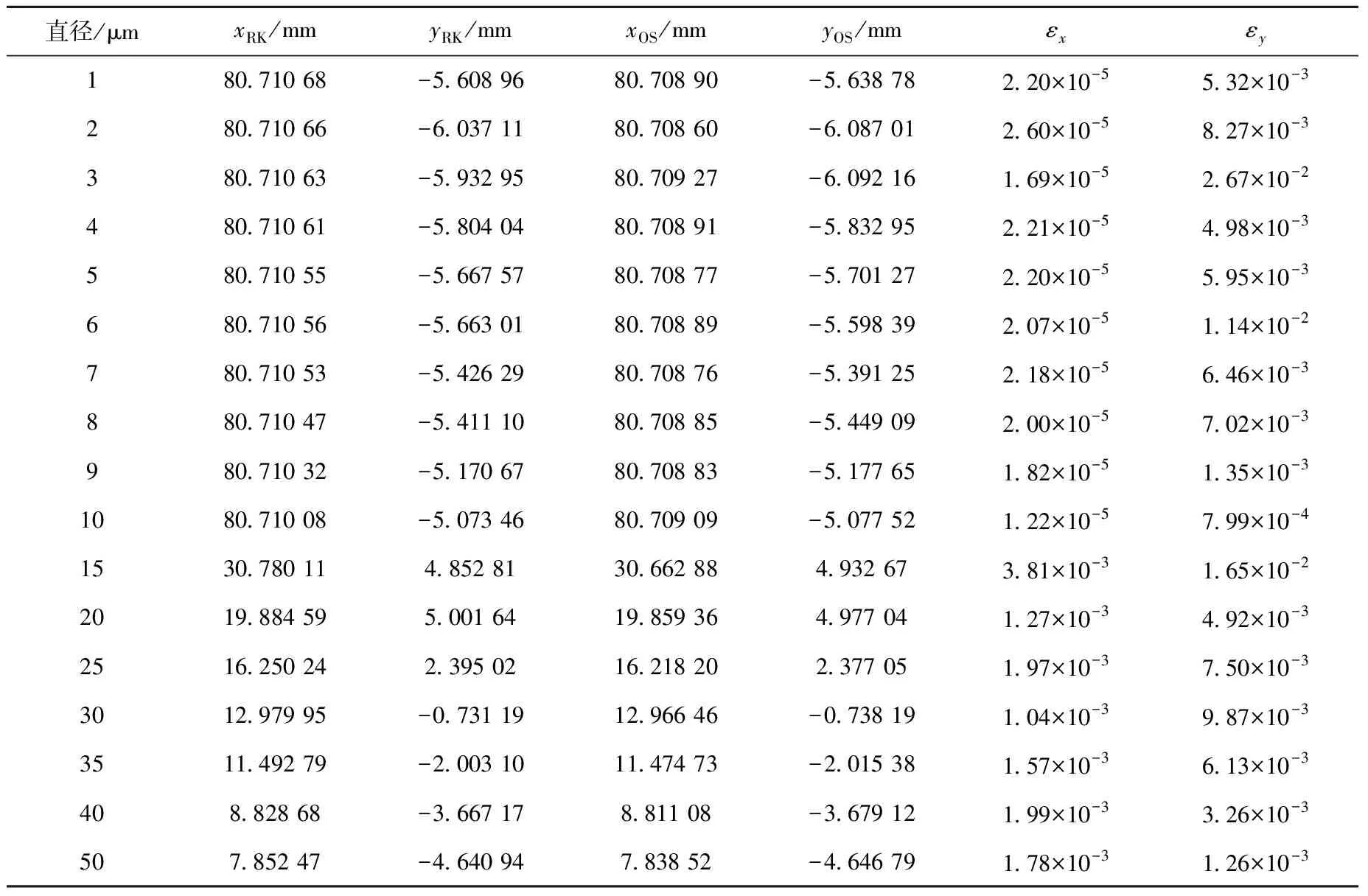
表2 液滴初始速度為3 m/s時兩種算法計算所得不同直徑液滴終端位置平均值及其相對誤差

表3 液滴初始速度為5 m/s時兩種算法計算所得不同直徑液滴終端位置平均值及其相對誤差

表4 液滴初始速度為7 m/s時兩種算法計算所得不同直徑液滴終端位置平均值及其相對誤差

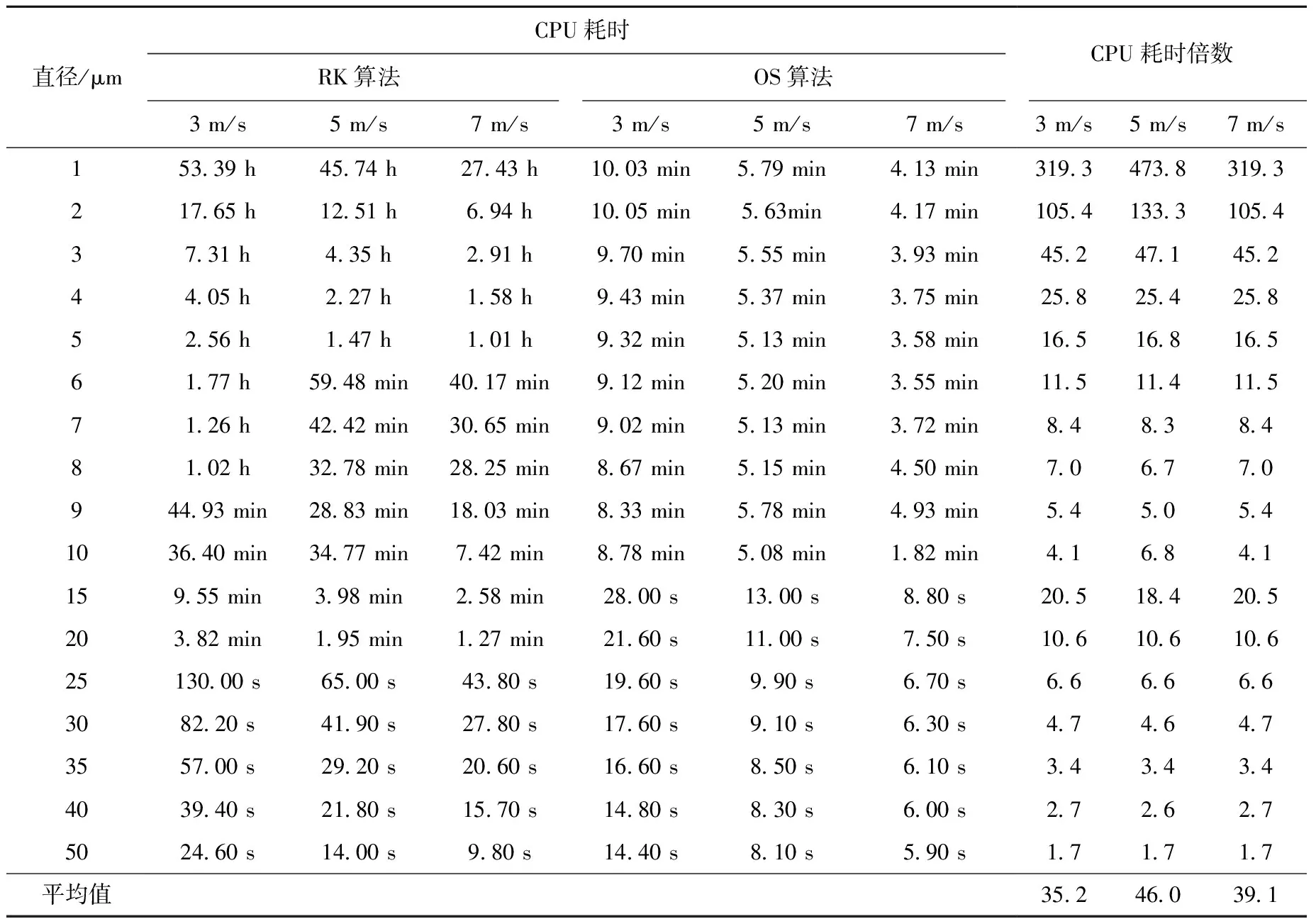
表5 兩種算法對不同直徑單個液滴的平均CPU耗時及CPU耗時倍數

4 結束語

本文針對三維空間液滴運動模型提出了一種新的數值求解方法——OS算法，并采用該算法求解波形板內液滴運動軌跡，同時與RK算法所得結果進行了對比。得到主要結論如下：

1) 本文構造的OS算法具有局部二階精度；

2) 保持OS算法穩定的最大時間步長的量級可取10-1～10-3s，而保持RK算法穩定的最大時間步長的量級為10-6～10-9s，因此OS算法的穩定性優于RK算法；

3) 在計算精度相同的情況下，OS算法的計算效率優于RK算法。

因此OS算法的提出為數值求解三維空間液滴運動模型，進而計算波形板的分離效率提供了一種相對穩定、高效的算法。

參考文獻：

[1] 龐鳳閣，于瑞俠，張志儉. 波形板汽水分離器的機理研究[J]. 核動力工程，1992，13(3)：9-13.

PANG Fengge, YU Ruixia, ZHANG Zhijian. The study of mechanism of corrugated baffles separator[J]. Nuclear Power Engineering, 1992, 13(3): 9-13(in Chinese).

[2] 陳韶華，黃素逸，趙緒新. PWR蒸汽發生器水滴重力分離研究[J]. 華中理工大學學報：自然科學版，1997，25(1)：69-71.

CHEN Shaohua, HUANG Suyi, ZHAO Xuxin. A study on the gravity separation of water droplets in steam generators for PWR[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 1997, 25(1): 69-71(in Chinese).

[3] 陳韶華，黃素逸，趙緒新. 波形板汽水分離器汽水兩相分離機理研究[J]. 華中理工大學學報：自然科學版，1998，26(1)：5-7.

CHEN Shaohua, HUANG Suyi, ZHAO Xuxin. On separation mechanism of steam water two phase flows in a steam water separator with corrugated baffle[J]. Journal of Huazhong University of Science and Technology: Nature Science Edition, 1998, 26(1): 5-7(in Chinese).

[4] 王曉墨，黃素逸. 波形板汽水分離器中液滴軌跡的數值模擬[J]. 核動力工程，2003，24(6)：582-585.

WANG Xiaomo, HUANG Suyi. Numerical simulation of droplets track in separator with wave-shape vanes[J]. Nuclear Power Engineering, 2003, 24(6): 582-585(in Chinese).

[5] 張謹奕，薄涵亮，孫玉良，等. 三維空間液滴運動模型[J]. 清華大學學報：自然科學版，2013，53(1)：96-101.

ZHANG Jinyi, BO Hanliang, SUN Yuliang, et al. Three-dimensional droplet motion model[J]. Journal of Tsinghua University: Science and Technology, 2013, 53(1): 96-101(in Chinese).

[6] 張謹奕，薄涵亮. 液滴模型在波形板汽水分離器中的應用[J]. 原子能科學技術，2012，46(增刊)：776-781.

ZHANG Jinyi, BO Hanliang. Application of droplet model in wave-type vane steam separator[J]. Atomic Energy Science and Technology, 2012, 46(Suppl.): 776-781(in Chinese).

[7] 李大侃. 常微分方程數值解[M]. 杭州：浙江大學出版社，1994：21-42.

[8] 李嘉. 波形板汽水分離器的理論和實驗研究[D]. 武漢：華中科技大學，2007.

[9] 陸金甫，關治. 偏微分方程數值解法[M]. 2版. 北京：清華大學出版社，2004：19-28.

[10] 陶文銓. 數值傳熱學[M]. 2版. 西安：西安交通大學出版社，2001：48-52.

[11] 李慶揚，關治，白峰杉. 數值計算原理[M]. 北京：清華大學出版社，2000：372-376.