X射線測厚儀刻度校正模型的研究
徐廣鐸,王立強,童建民
(清華大學 核能與新能源技術研究院,北京 102201)
X射線測厚儀在冶金行業板帶材生產的厚度質量控制中得到廣泛使用,其測量控制精度的高低將直接影響產品的質量等級。當X射線穿過被測物質時,射線與物質的相互作用使透射射線強度減弱,當其他條件固定時,透射射線強度由被測物質厚度唯一決定,若已知射線的衰減規律,通過測量透射射線強度即可得到被測物質厚度,這即是X射線測厚的基本原理。當射線為單能窄束時,射線衰減遵循指數定律,但X射線能量具有一定的范圍分布,在實際測量系統中也不滿足窄束測量條件,所以射線強度隨被測物質厚度的變化并不遵循指數衰減規律。因此,在實用中通常需先測量若干厚度已知的標定片進行標定,再通過擬合或插值等方法得到射線強度與被測板材厚度的關系,這種方法的精度取決于標準片的厚度間距,當采用足夠多的標準片使厚度間距足夠小時,能達到很高的精度。文獻[1]提出了一種描述寬束單能γ射線衰減的非線性模型,文獻[2]將上述方法應用于薄膜X射線測厚儀中。文獻[3-4]在瑞美公司生產的RM312型X射線板形儀中采用了分段多項式擬合的方法進行厚度刻度校正。但文獻[1]的方法不能直接應用到非薄膜的X射線測厚儀的刻度校正中,線性插值與文獻[3-4]中的多項式擬合法雖可達到一定的測量精度,但刻度校正過程中需較多的標定片,給系統維護穩定運行帶來不便。
本文研究一種新的刻度校正數學模型,并通過實驗數據處理將該刻度校正模型方法與文獻中提出的3種方法進行對比,比較4種方法隨刻度校正數據點減少,其測量精度和穩定性的變化情況。
1 新的刻度校正非線性模型
文獻[1]對單能γ射線測厚儀提出了一種非線性模型,本文模型在其模型基礎上,擴展到X射線測厚系統。一般測厚儀中使用的X射線能量具有能譜分布、非單能,而測量系統也通常不滿足窄束條件,因此射線在透射中存在硬化和散射現象,使X射線的衰減情況非常復雜,不能用指數衰減定律準確描述,需進行修正,為此,設X射線穿過厚度為x的被測物質后的射線強度I滿足:
I=I0e-μ(x)x
(1)
式中,μ(x)替代了指數衰減公式中的線性吸收系數。當X射線能譜分布一定時,測量同種材料物質,射線衰減情況與被測物質厚度一一對應,因此μ(x)為被測物質厚度x的函數,下面需確定μ(x)的形式。
由于射線的硬化和散射,μ(x)隨物質厚度的增加而減小,最后趨近于一極值,即:
μ(x)=μ∞
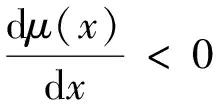
(2)
滿足式(2)的函數有很多,其中形式較簡單的函數為:
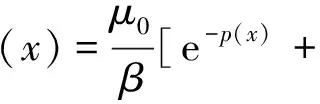
(3)
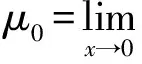
為使式(2)成立,p(x)還需滿足:
∞
p′(x)>0x∈(0,+∞)
(4)
上述模型非線性,難以求得解析解,需數值求解,對式(3)兩邊取對數得:
(5)
根據式(3)、(4)有:
μ(x)=μ∞μ0
(6)
將式(6)代入式(5)得:
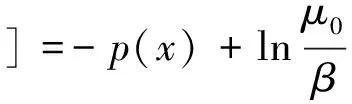
(7)
μ0、μ∞的值取決于材料性質和射線能量,對于同種材料在相同射線能量下μ0、μ∞為確定的常數。
設對厚度為xi(i=1,2,…,n)的標定片進行校正測量時得到的透射射線強度為Ii,通過式(1)計算出μ(xi),通過外延法確定μ∞,通過式(7)進行多項式擬合可得到p(x)、μ0與β,即確定了模型的所有參數。
將式(1)兩邊取對數可得:
(8)
若實驗測得射線穿過某厚度為x的被測物質后的強度為I,根據標定點數據先選取射線衰減值最接近I的標定片的厚度為迭代初值x0,根據精度需選取迭代收斂判定閾值ε。按式(8)進行不動點迭代,式(8)可記為x=G(x),迭代公式為xn+1=G(xn),反復迭代直至xn+1-xn的絕對值小于ε,判定收斂,輸出xn+1,即得到滿足精度要求的x。
2 文獻中3種校正方法模型
2.1 線性插值模型
若被測物厚度x在第i個標定片厚度xi附近,即x=xi+Δx,衰減后的射線強度I=Ii+ΔI,由式(1)可得:
Ii=I0e-μ(xi)xi
(9)
Ii+ΔI=I0e-μ(xi+Δx)(xi+Δx)
(10)
當Δx不大時,式(10)可近似為:
Ii+ΔI≈I0e-μ(xi)(xi+Δx)=
Iie-μ(xi)Δx=Ii[1-μ(xi)Δx]
(11)
進而得到:
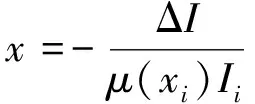
(12)
于是被測厚度為:
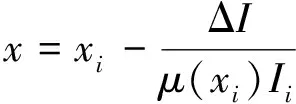
(13)
這樣測得透射射線強度I即可通過式(13)計算被測物厚度x。該方法計算簡單,但為了達到要求的精度,要求標定片厚度間距足夠小,從而需較多數量的標定片,使刻度校正工作十分繁瑣。
2.2 單能射線非線性模型
對于單能寬束γ射線的衰減規律,文獻[1]給出了一種非線性模型:
I=I0e-μ(x)x
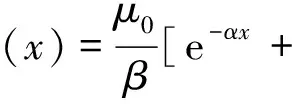
(14)
其中,α、β為正常數。新非線性模型采用了與式(14)類似的公式,區別在于新模型中用多項式p(x)代替了式(14)中的-αx。式(14)在γ射線測厚儀刻度校正中取得了較好的效果。但γ射線為單能,透射中無硬化現象,因此式(14)用于描述X射線透射過程精度相對新模型精度較低。
2.3 多項式模型
以標定片厚度xi(i=1,2,…,n)為因變量,對應的射線強度對數值lnIi為自變量進行多項式擬合,則:
xi=PnlnIi
(15)
其中,Pn為n次多項式。
為了保證精度,一般采用五次多項式擬合,當厚度跨度范圍較大時需分段擬合,理論上不分段時至少需6片標定片,分段擬合時所需標定片數量加倍,因實用中多采用多項式擬合,標定工作量較大。
3 不同模型數據處理結果的對比分析
通過實驗室的X光機測厚儀對0~4.1 cm厚度區間內已知厚度的25塊標定片進行了標定測量,其射線強度為20位ADC轉換后的測量數值(已扣除本底零點數值)(表1)。X光機電壓為80 keV,電流為0.8 mA,濾片為0.2 mm不銹鋼片,經過濾片后X射線能譜形狀近似為具有一定能量寬度的正態分布的曲線,標定片為鐵片,所有標定片采用同一材料制成。
從上述測量值中選取不同的數據點分別采用前文所述的各刻度校正模型求解被測物質的厚度,根據計算厚度與已知厚度求出各模型厚度測量的均方差和相對偏差,對比各模型的精度。改變所取數據點重復上述計算,考察不同情況下各模型的精度變化,比較各模型在數據點變化時的穩定性。
3.1 選擇全部數據點時各模型計算結果對比
選取所有數據點,分別采用新非線性模型、單能射線非線性模型和多項式模型進行擬合,新非線性模型中p(x)選取三次以上多項式擬合精度較高。為使模型簡單,下面以三次多項式擬合結果進行對比,結果示于圖1。可看出,多項式模型與新非線性模型的擬合精度相近,單能射線非線性模型的誤差明顯大于前兩者。
3.2 選擇部分數據點時各模型計算結果對比
實際應用中,由于工作環境的變化,需定時刻度校正,因此希望能簡化刻度校正過程,使用少量的標定片確定射線的衰減曲線,為檢驗在減少標定片個數時各模型精度,選取部分數據點,使用不同模型進行擬合并對比計算結果。選取數據點時,考慮不同數量數據點及數據點的不同分布等多種情況,并考察當數據點不包含整個厚度區間時的對刻度區間外部數據點計算的誤差,以檢驗各模型的穩定性。
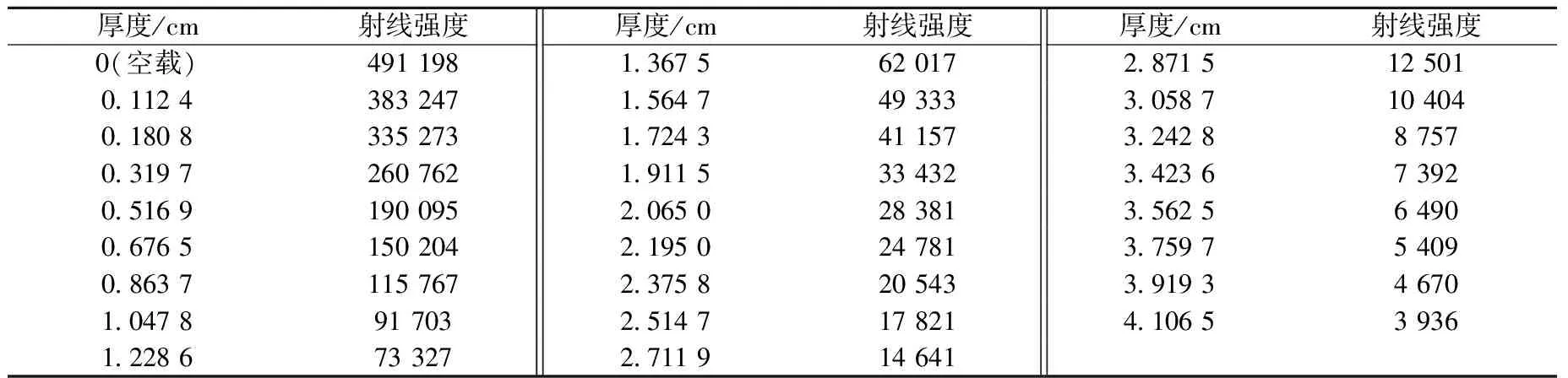
表1 X射線測厚儀標定測量數據
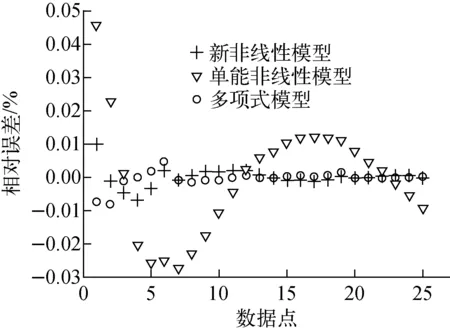
圖1 各擬合模型的相對誤差
1) 數據點包含全厚度區間
數據點包含最小厚度點和最大厚度點,其中空載數據在各模型中作為常數參與計算。首先按厚度均勻選取數據點,數據個數分別取4、5、6、8、10,按各模型進行計算,計算結果列于表2。由表2可看出,新非線性模型在數據點減少時計算的相對誤差基本穩定,多項式模型的計算誤差隨選取數據點不同有小幅波動,但變化幅度較小并在精度上略優于新非線性模型。單能非線性模型計算的相對誤差基本穩定,線性插值法計算的相對誤差隨數據點的減少明顯增大,這兩者相對誤差較前兩模型均較大。
考慮非均勻選取數據點的情況,分別取5和7數據點,考察數據點集中在厚度較小、較大區間時各模型的誤差,結果列于表3。由表3可看出,對于非均勻數據點,新非線性模型的計算誤差與均勻選取時相比變化很小,穩定性高,而多項式模型計算誤差變化相對較大,但總體上兩模型精度相當。線性插值模型和單能非線性模型的計算誤差仍較大。
2) 數據點不包含全厚度區間
在射線測厚中,若被測物厚度超出標定范圍時通常會有較大的誤差,因此考察當數據點不包含整個厚度區間時的各模型對外延部分數據點的計算誤差。分別選取4和6數據點,考察數據點不含最大厚度、不含最小厚度和二者均不含時的情況,計算結果列于表4。從表4可看出,當選取數據點不包含全厚度區間時,各模型計算結果的誤差均增大,而新非線性模型的精度變化相對較小,并在多數情況下優于其他模型。誤差的增大主要來自于選取厚度區間外的數據點,圖2對比了當選取不同數據點時,新非線性模型和多項式模型擬合結果在各數據點的相對誤差。從圖2可看出,在標定范圍外兩個模型計算結果的相對誤差均會增大,對于多項式模型,超出標定范圍時誤差顯著增加,并呈發散趨勢,而新非線性模型在標定范圍外誤差穩定,無發散現象,在標定范圍外各數據點的相對誤差均在1%以內。

表2 均勻選取數據點時各模型均方相對誤差

表3 非均勻選取數據點時各模型均方相對誤差
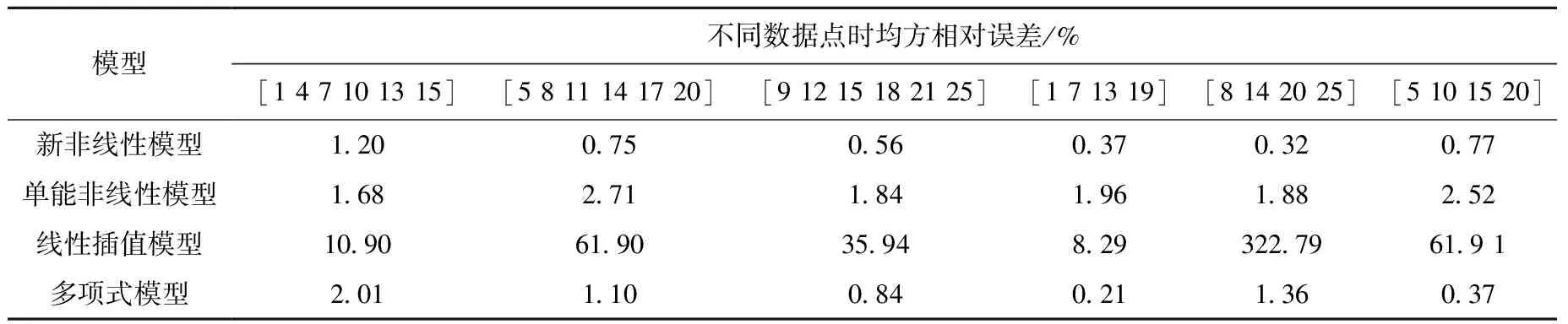
表4 數據點不包含全厚度區間時各模型均方相對誤差
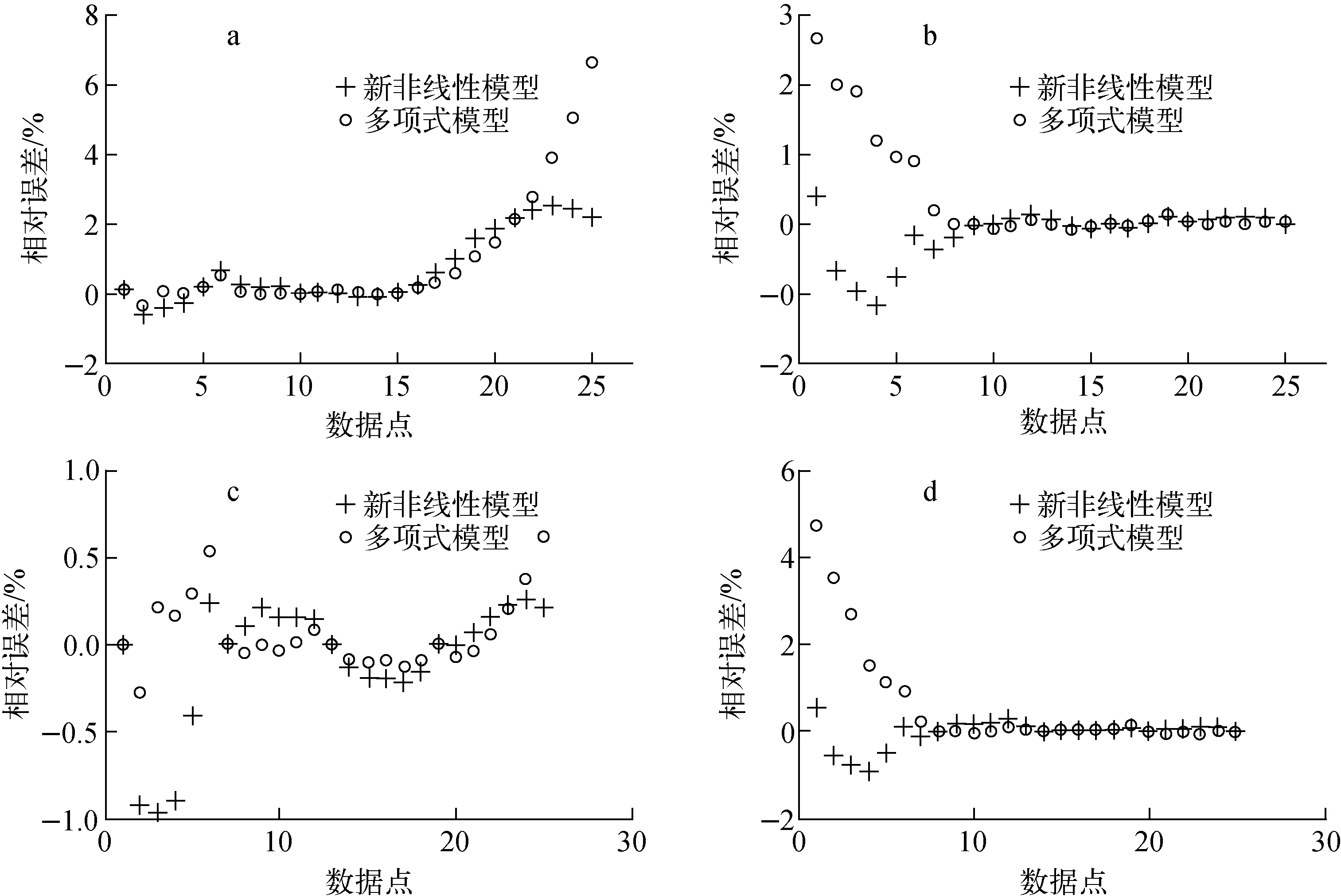
a——[1 4 7 10 13 15];b——[9 12 15 18 21 25];c——[1 7 13 19];d——[8 14 20 25]
4 結論
本文通過實驗室X光機測厚儀對已知厚度的25塊標定片的測量數據,對比了選取不同標定數據時各模型擬合結果的精度,當數據點足夠多時,多項式模型的精度略優于本文的新非線性模型,然而當數據點減少且分布不均勻時,多項式模型的誤差顯著增加,新非線性模型精度基本穩定,并在多數情況下優于多項式模型,通常只取4數據點即能以較高精度確定衰減曲線。當測量厚度在標定范圍外時,新非線性模型的精度顯著優于其他模型。
參考文獻:
[1] SHIRAKAWA Y. A build-up treatment for thickness gauging of steel platesbased on gamma-ray transmission[J].Applied Radiation and Isotopes, 2000, 53(4-5): 581-586.
[2] 陸永耕. X射線測厚原理模型分析與實驗[J]. 上海電機學院學報,2008,11(3):177-180.
LU Yonggeng. Analysis of the calculation model of X-ray thickness gauge and the experiment[J]. Journal of Shanghai Dianji University, 2008, 11(3): 177-180(in Chinese).
[3] RM312 instantaneous profile gauge engineering manual issue 2.2[M]. Gloucester: Thermo Radiometrie Limited, 2002: 66-88.
[4] RM312 instantaneous profile gauge technician’s manual issue 3[M]. Gloucester: Thermo Radiometrie Limited, 2005: 51.

