解析函數(shù)展開節(jié)塊法的數(shù)值穩(wěn)定性分析

孫 偉，李 慶，王 侃

(1.清華大學(xué) 工程物理系，北京 100084；

2.中國(guó)核動(dòng)力研究設(shè)計(jì)院 核反應(yīng)堆系統(tǒng)設(shè)計(jì)技術(shù)重點(diǎn)實(shí)驗(yàn)室，四川 成都 610041)

方形幾何節(jié)塊法中，橫向積分是其中的關(guān)鍵技術(shù)，但在六角形幾何中直接采用橫向積分技術(shù)時(shí)橫向泄漏會(huì)出現(xiàn)奇異項(xiàng)，奇異項(xiàng)的出現(xiàn)給節(jié)塊中子注量率的求解帶來(lái)困難[1]。針對(duì)此問(wèn)題，韓國(guó)KAIST的Cho等[2]提出了解析函數(shù)展開節(jié)塊(AFEN)法。AFEN法是在六角形幾何內(nèi)不分離變量而直接利用嚴(yán)格滿足中子擴(kuò)散方程的解析基函數(shù)，把節(jié)塊內(nèi)的各群中子注量率近似展開。然后根據(jù)節(jié)塊間耦合條件，將節(jié)塊面平均凈流表示為節(jié)塊體平均中子注量率和面平均中子注量率的函數(shù)關(guān)系，代入節(jié)塊中子平衡方程形成全堆關(guān)于節(jié)塊體平均中子注量率和面平均中子注量率的方程組，分別用加速的高斯塞德爾方法和源迭代方法求解中子注量率和堆芯有效增殖因數(shù)keff。

研究發(fā)現(xiàn)利用AFEN法數(shù)值求解一些特殊問(wèn)題時(shí)，如keff接近于某一節(jié)塊的無(wú)限介質(zhì)增殖因數(shù)kinf(節(jié)塊在堆芯中實(shí)際凈泄漏接近于零)時(shí)，面平均凈流對(duì)中子注量率的關(guān)系系數(shù)出現(xiàn)震蕩，使得關(guān)于中子注量率方程組的系數(shù)矩陣出現(xiàn)病態(tài)，進(jìn)而方程組的求解不收斂，無(wú)法得出中子注量率的解。方形幾何中，基于橫向積分技術(shù)的非線性迭代解析節(jié)塊法的這類不穩(wěn)定性問(wèn)題，Joo等[3]做了相關(guān)研究，對(duì)病態(tài)節(jié)塊采用線性近似或節(jié)塊展開法(NEM)代替解析節(jié)塊法求解；而六角形幾何中，針對(duì)中子注量率直接展開的AFEN法的這類不穩(wěn)定性問(wèn)題，尚未見相關(guān)研究，本文提出兩種解決方法來(lái)解決上述問(wèn)題，即截?cái)嘟品椒ê吞├照归_方法。

1 AFEN法數(shù)值不穩(wěn)定性分析

1.1 AFEN法公式推導(dǎo)

對(duì)于反應(yīng)堆內(nèi)一個(gè)均勻的六角形節(jié)塊，其三維多群穩(wěn)態(tài)中子擴(kuò)散方程[1]可寫成如下形式：

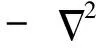
(1)

其中：r為空間位置變量；V為節(jié)塊體積；Φ(r)=[Φ1(r)，Φ2(r)，…，ΦG(r)]T為G群中子注量率構(gòu)成的向量。矩陣Λ(keff)的元素Λgg′為：

νΣfg′)/Dg

(2)

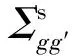
式(1)的解析解主要取決于矩陣Λ(keff)的特征值λm及相應(yīng)特征向量um的數(shù)值類型。對(duì)于一般多群?jiǎn)栴}，λm既可能為實(shí)數(shù)也可能為復(fù)數(shù)，本文僅介紹λm均為實(shí)數(shù)的情況。

利用Λ(keff)的λm及um可將每群中子注量率展開為：

(3)

其中：U為矩陣Λ(keff)所有特征向量構(gòu)成的矩陣；第m列對(duì)應(yīng)于特征向量um；μgm為矩陣U的元素；Aml、Bml、Am0為展開系數(shù)；el為節(jié)塊展開時(shí)所選坐標(biāo)軸上的單位向量，l取4時(shí)其具體表達(dá)式參見文獻(xiàn)[1]。

SN、CS為雙曲或三角函數(shù)：

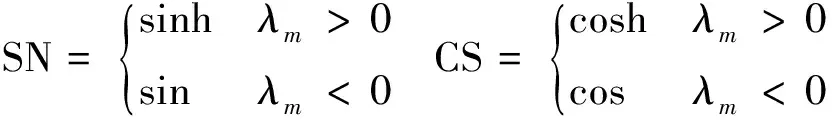
(4)

利用凈流和中子注量率的關(guān)系可得節(jié)塊內(nèi)面平均凈流與面平均中子注量率、體平均中子注量率的關(guān)系：

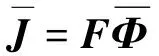
(5)

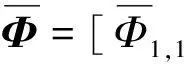
將式(5)代入式(6)可得全堆芯所有節(jié)塊關(guān)于面平均中子注量率、體平均中子注量率的方程組，可簡(jiǎn)寫為式(7)，對(duì)式(7)的求解采用源迭代法，具體求解過(guò)程參見文獻(xiàn)[4]。

,2,…,G

(6)

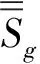
MX=N

(7)

式中：系數(shù)矩陣M與群截面、堆芯幾何參數(shù)、組件不連續(xù)因子有關(guān)；X為堆芯所有面平均中子注量率構(gòu)成的向量；N與體平均中子注量率有關(guān)。

1.2 AFEN法數(shù)值不穩(wěn)定性原因探究

式(5)中系數(shù)矩陣F的每個(gè)元素都是雙曲或三角函數(shù)的表達(dá)式，與組件半寬度H、λm有關(guān)。表1列出矩陣元素F(G，1)(具體表達(dá)式詳見式(8)和(9)，其他元素的表達(dá)式在形式上與F(G，1)的相同)隨λm的變化情況(H取7.35)。可看出，當(dāng)λm>0時(shí)，隨λm的減小，F(xiàn)(G，1)變化平緩，但λm減小到某一值時(shí)，F(xiàn)(G，1)出現(xiàn)畸變，在λm接近于0時(shí)F(G，1)變?yōu)闊o(wú)窮大；當(dāng)λm<0時(shí)，在接近于0時(shí)F(G，1)也為無(wú)窮大，通過(guò)觀察F(G，1)的求解式可發(fā)現(xiàn)，當(dāng)λm接近于0時(shí)，F(xiàn)(G，1)求解式各項(xiàng)分子、分母均接近于0，當(dāng)兩個(gè)接近于0的數(shù)運(yùn)算時(shí)會(huì)引入舍入誤差[5]。矩陣F元素的畸變會(huì)引起式(7)中系數(shù)矩陣M的元素也相差幾個(gè)數(shù)量級(jí)甚至為無(wú)窮大，導(dǎo)致M變?yōu)閯傂跃仃嚕?7)內(nèi)迭代求解不收斂。

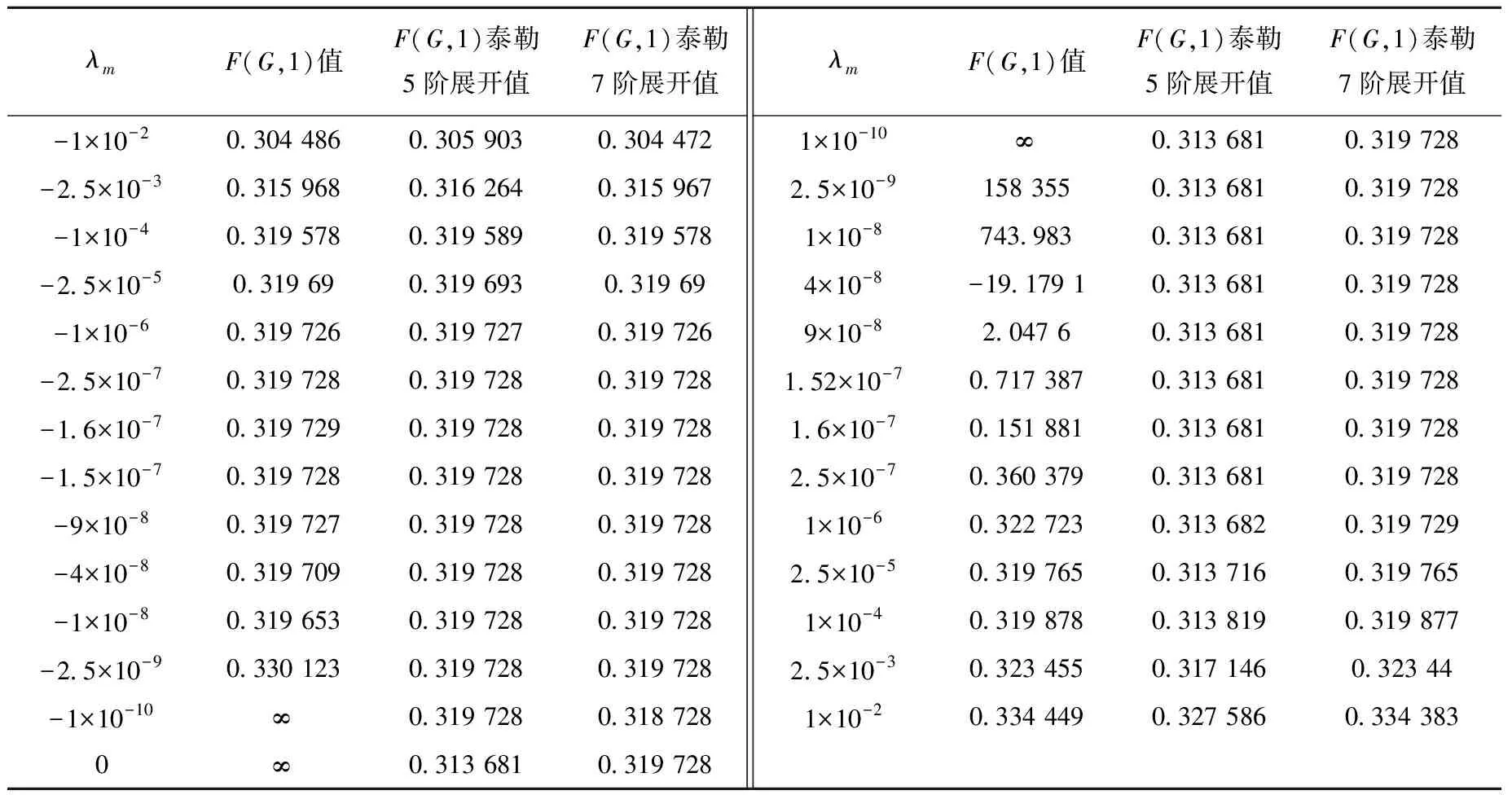
表1 F(G，1)值隨特征值的變化情況

當(dāng)λm>0時(shí)，有：

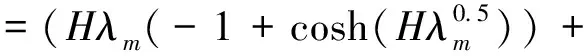
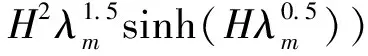
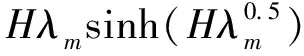
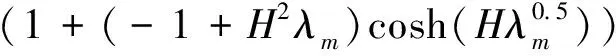
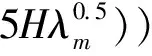
(8)

當(dāng)λm<0時(shí)，有：

F(G,1)=(H|λm|(-1+cos(H|λm|0.5))-

H2|λm|1.5sin(H|λm|0.5))/6(-2+(2+

H2|λm|)cos(H|λm|0.5))+|λm|0.5×

(-1+cos(H|λm|0.5))/6(-H|λm|0.5×

cos(H|λm|0.5)+sin(H|λm|0.5))+

H|λm|sin(H|λm|0.5)/3(-H|λm|0.5×

cos(H|λm|0.5)+sin(H|λm|0.5))+

|λm|0.5(H|λm|0.5cos(H|λm|0.5)×

(-1+H|λm|0.5cos(0.5H|λm|0.5))-

sin(H|λm|0.5))/2(-2+H2|λm|+

(2+H2|λm|)cos(H|λm|0.5)-

H|λm|0.5sin(H|λm|0.5))

(9)

系數(shù)矩陣F的元素值出現(xiàn)畸變，是由于矩陣Λ(keff)出現(xiàn)接近于0的特征值，本文僅給出2群截面時(shí)的公式推導(dǎo)解釋特征值接近于0的原因，2群時(shí)矩陣Λ(keff)的具體形式及截面間的轉(zhuǎn)換關(guān)系如下：

Λ(keff)=

(10)

Σr1=Σt1-Σ1→1;Σr2=Σt2-Σ2→2;

χ1=1;χ2=0;Σ2→1=0

(11)

其中，Σr1、Σr2為1、2群移除截面。由式(10)、(11)可知矩陣Λ(keff)行列式為：

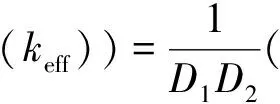
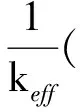
(12)

當(dāng)Λ(keff)出現(xiàn)接近于0的特征值時(shí)，Λ(keff)行列式接近于0，得：

·

(13)

又根據(jù)文獻(xiàn)[3]可知，2群截面時(shí)節(jié)塊的kinf為：

·

(14)

由式(13)、(14)可知，當(dāng)keff接近于某一節(jié)塊的kinf時(shí)，矩陣Λ(keff)會(huì)出現(xiàn)接近于0的特征值，引起系數(shù)矩陣M的病態(tài)，出現(xiàn)不收斂情況。而kinf接近于keff的含義是節(jié)塊在堆芯中凈流為0，這多出現(xiàn)在堆芯中部，且堆芯含有多種富集度燃料，因?yàn)橐话愣研径加行孤瑑袅骱茈y為0。

1.3 AFEN法的數(shù)值穩(wěn)定性方法介紹

出現(xiàn)不收斂的直接原因是矩陣Λ(keff)的特征值很小時(shí)，M變?yōu)閯傂跃仃嚕瑢?dǎo)致迭代不收斂，為解決這一問(wèn)題，提出2種方法。

1) 截?cái)嘟品椒ā谋?可知，在畸變前當(dāng)特征值很小時(shí)，元素值基本不變，此時(shí)可將出現(xiàn)畸變的值截?cái)啵苯佑没兦耙豢痰闹荡妗＞唧w方法是當(dāng)0<λm<10-6時(shí)，λm近似取為10-6，當(dāng)-10-8<λm<0時(shí)，λm近似取為-10-8(由于λm在(-0.01，0.01)范圍內(nèi)時(shí)元素值變化不大，且堆芯內(nèi)出現(xiàn)特征值接近于0的節(jié)塊極少，因此截?cái)帱c(diǎn)的選擇基本不影響堆芯計(jì)算結(jié)果的精度，本文截?cái)帱c(diǎn)是參考F(G，1)變化趨勢(shì)給出的)。截?cái)嘟频谋举|(zhì)是對(duì)病態(tài)節(jié)塊采取近似常解析基函數(shù)展開。

2) 泰勒展開方法。當(dāng)-10-8<λm<10-6時(shí)，對(duì)矩陣F元素求解式中的雙曲函數(shù)或三角函數(shù)進(jìn)行泰勒展開，泰勒展開的目的是對(duì)求解式繼續(xù)化簡(jiǎn)，避免出現(xiàn)分子、分母接近于0的項(xiàng)。表1列出5階和7階泰勒展開時(shí)元素F(G，1)的計(jì)算結(jié)果，可看出7階展開求出的F元素值更接近于真實(shí)值。泰勒展開的核心思想是高階多項(xiàng)式展開，與Joo等提出的對(duì)病態(tài)節(jié)塊直接采取NEM方法相比，7階泰勒展開保留原AFEN法的求解格式，在保證精度的同時(shí)更容易實(shí)現(xiàn)。

2 數(shù)值驗(yàn)證

HANDF-D[4]是基于解析函數(shù)展開節(jié)塊法編制的可用于三維多群六角形幾何計(jì)算的程序，其正確性已得到多個(gè)基準(zhǔn)題的驗(yàn)證。為檢驗(yàn)上述兩種穩(wěn)定性方法的有效性，將其添加到HANDF-D程序中。驗(yàn)證對(duì)象為改造后的三維VVER440基準(zhǔn)題[1]，改造方法是減小VVER440材料1的兩群吸收截面(表2)，使keff接近于材料2的kinf(1.082 55)。將TRIVAC[6]的計(jì)算結(jié)果作為基準(zhǔn)解，TRIVAC程序是由加拿大開發(fā)的可計(jì)算三維多群六角形幾何堆芯的中子學(xué)程序，采用了多種方法，包括有限差分方法、有限元方法等。

表2 VVER440材料1截面變化

在使用原HANDF-D程序計(jì)算改造后VVER440基準(zhǔn)題(軸向分12層，每25 cm為1層)時(shí)，迭代中出現(xiàn)keff為1.082 56，接近于材料2的kinf(1.082 55)，矩陣Λ(keff)出現(xiàn)極小特征值1.429 2×10-7，迭代不收斂。表3列出采用兩種穩(wěn)定性方法時(shí)keff的結(jié)果，可看出兩種方法計(jì)算均收斂且keff與TRIVAC的相比相對(duì)偏差僅為-0.02%。圖1示出功率分布的比較結(jié)果，功率分布最大相對(duì)偏差為2.03%，出現(xiàn)在燃料與反射層交界處，這與文獻(xiàn)[4]中指出的HANDF-D程序本身固有2.5%左右的功率偏差相當(dāng)。從keff和功率分布結(jié)果可看出，兩種穩(wěn)定性方法計(jì)算結(jié)果精確可靠，均能很好地解決解析函數(shù)展開節(jié)塊法計(jì)算不穩(wěn)定性問(wèn)題。

表3 改造后VVER440基準(zhǔn)題keff計(jì)算結(jié)果

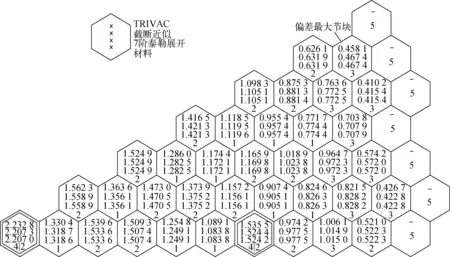
圖1 改造后VVER440基準(zhǔn)題功率分布比較

3 結(jié)論

通過(guò)計(jì)算分析發(fā)現(xiàn)利用AFEN法求解六角形堆芯中子注量率，當(dāng)keff接近于某一節(jié)塊kinf時(shí)，會(huì)使得此節(jié)塊的矩陣Λ(keff)出現(xiàn)極小特征值。利用此極小特征值求解全堆芯關(guān)于中子注量率方程組的系數(shù)矩陣時(shí)，由于引入舍入誤差使得系數(shù)矩陣變成剛性矩陣，導(dǎo)致迭代不收斂。針對(duì)此類問(wèn)題，提出2種解決方法：截?cái)嘟品椒ê吞├照归_方法。對(duì)改造后的VVER440基準(zhǔn)題驗(yàn)證表明，兩種方法均可有效解決不收斂問(wèn)題，計(jì)算結(jié)果和參考解符合很好這一事實(shí)也充分說(shuō)明這兩種方法有較高的精度。

參考文獻(xiàn)：

[1] 夏榜樣. 三維多群六角形節(jié)塊法及其應(yīng)用研究[R]. 西安：西安交通大學(xué)，2006.

[2] CHO N Z, NOH J M. Analytic function expansion nodal method for hexagonal geometry[J]. Nucl Sci Eng, 1995, 121(3): 245-253.

[3] JOO H G, JIANG Guobing, DOWNAR T J. Stabilization techniques for the nonlinear analytic nodal method[J]. Nucl Sci Eng, 1998, 130(1): 47-59.

[4] 孫偉，倪東洋，李慶，等. 三維多群六角形幾何中子擴(kuò)散程序開發(fā)[J]. 原子能科學(xué)技術(shù)，2013，47(10)：1 707-1 712.

SUN Wei, NI Dongyang, LI Qing, et al. Development of 3D multi-groups neutron diffusion code for hexagonal geometry[J]. Atomic Energy Science and Technology, 2013, 47(10): 1 707-1 712(in Chinese).

[5] 周鐵，徐樹方，張平文，等. 計(jì)算方法[M]. 北京：清華大學(xué)出版社，2006.

[6] HéBERT A, SEKKI D. A user guide for TRIVAC version4[R]. Montreal: Insitut de Genie Nucleaire Department Degenie Mecanique-Ecole Polytechnique de Montreal, 2009.