鈾生產工藝設備中滯留量測量的自吸收校正方法

何麗霞，甘 霖,*，隋洪志，陳立君

(1.中國原子能科學研究院 放射化學研究所，北京 102413；2.中國核工業集團公司，北京 100086)

鈾燃料循環生產工藝過程中的某些環節有部分物料的殘渣和溶解液沉積，溶解階段形成的滯留量成為影響鈾生產衡算的重要因素，為實現鈾生產線核材料的閉合衡算，必須對滯留量進行準確測量。測量存在較大難度，容器的幾何結構、其所處的空間條件、滯留量的介質成分等均會對測量結果產生影響，而其中最大的困難在于物料的自吸收影響校正。Reilly等[1]對可回收樣品測量的自吸收修正、自吸收校正技術和存在的問題給出了理論分析。國內也有針對特定對象的自吸收校正方法研究[2-3]，主要通過數學方法和蒙特卡羅模擬技術解決。本文擬在物料厚度、介質成分、幾何參數不確定的條件下，初步建立自吸收二維校正模型。

1 自吸收影響

若某放射性物料分布為理想面源，其自發射的γ射線在遠場一階近似條件下，自吸收的表達式[3]為：

μiRS?1

(1)

式中：Gi為第i條γ射線放射性物料的自吸收因子；RS、t為放射性物料的幾何參數；μi為特定能量γ射線的線性衰減系數；i為某同位素不同能量的特征γ射線，i=1,2,3,4對應的235U的特征γ射線能量分別為143、163、186和205 keV。

而在某些鈾生產工藝設備中，鈾的滯留量幾何分布不規則，可能是酸性溶液、粘稠物或干燥物等。此時，γ射線在其中的自吸收規律與式(1)不同，類似指數衰減分布，但Gi均可表示為：

(2)

式中：Ii為實際測量條件下某γ射線的計數率；I0為無自吸收時該γ射線的計數率。

2 自吸收修正過程

鑒于鈾生產工藝設備中滯留量不確定性強的特點，量化分析數據需歸一化處理，物料含量使用質量厚度，單位取g·cm-2。設自吸收因子與質量厚度之間的關系為：

(3)

式中：Tj為物料的質量厚度；Gij為質量厚度j條件下第i條γ射線的自吸收因子；aij、bij、ci為待定系數，通過系統刻度得到。

將式(3)定義為某特征γ射線的自吸收縱向變化曲線，即其自吸收因子隨質量厚度的變化關系。同一放射性同位素發射的特征γ射線分支比固定并已知[4]，在某質量厚度條件下，自吸收因子隨能量的變化為：

Gji=ajiEi+bji

(4)

其中，Ei為γ射線的能量。該式定義為某質量厚度下，γ射線的自吸收橫向變化曲線。

因特征γ射線的相關性，兩條曲線必然存在交點，即物理意義上的自吸收因子，此時，Gij=Gji，而aij≠aji，bij≠bji。不同能量γ射線的自吸收效應不同，能量越低，自吸收越顯著[5]。

2.1 確定無自吸收時的探測效率

無自吸收時，首先，需保證源與探測器的距離足夠大，測量對象近似為點源，可使源的徑向分布對測量結果的影響最小化；其次，物料分布應足夠薄，軸向近似無自吸收。

取已知活度的含235U的物料進行系統校準，按無自吸收的條件裝入容器，測定該測量條件下235U 4條特征γ射線的探測效率，探測效率εi[6]為：

(5)

式中：εi為特征γ射線的探測效率；Ci為特征γ射線的能峰總計數；A為被測物料中235U的比活度，Bq·g-1；Bi為特征γ射線的分支比；t為測量時間，s；W為235U的質量，g；Ω為測量幾何條件。無自吸收時，Gij=1。

2.2 建立自吸收模型

系統校準時，選取的物料厚度各不相同，特征量值分布具有一定的梯度范圍。首先不考慮自吸收的影響，利用測量所得的特征γ射線計數率推算235U活度，此值與活度真值相比即得該特征γ射線的自吸收因子。因此，系統校準的結果是，得到多種質量厚度條件下不同能量特征γ射線的自吸收因子矩陣。

另外，在某質量厚度條件下，不同能量γ射線的自吸收因子與主要γ射線的自吸收因子相比，可得到一組自吸收因子比，因此系統校準的自吸收因子矩陣也可用自吸收因子比矩陣表示。235U分析取186 keV γ射線為主要γ射線。

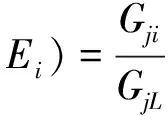
(6)

式中：Sji(Tj,Ei)為特征γ射線的一組自吸收因子比；GjL為主要γ射線的自吸收因子。

2.3 分析時引入自吸收校正

不同質量厚度的物料，其特征γ射線的自吸收獨具特點，反應在其自吸收因子比上，則是一組具有唯一性的數值，與系統校準結果之間存在差異。

假定未知物料質量厚度為Tm，測量獲取特征γ射線計數率，再利用系統校準時得出的探測效率推算自吸收因子比，即Smi(Tm,Ei)。然后，將這組自吸收因子比與系統校準的矩陣進行比較，可選擇合適的邊界條件，用拉格朗日線性插值方法[7]計算該物料的各非主要γ射線的自吸收因子Gmi，有：

當Smi(Tm,Ei)Sj+1,i(Tj+1,Ei)時，

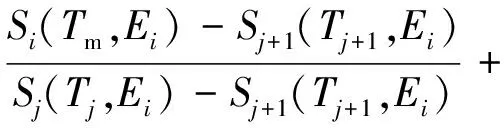
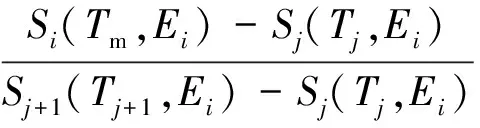
(7)

Gji、Gj+1,i、S等均通過系統刻度得到，由此，可推算主要γ射線的自吸收因子GmL：

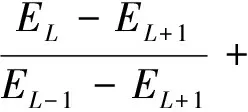
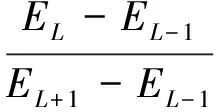
(8)

3 系統校準

在實驗室條件下開展滯留量的模擬測量，用已有條件構建適用于鈾生產工藝設備的測量模型，建立自吸收修正關系。

3.1 實驗條件

測量系統為HPGe探測器和多道譜儀，物料為天然U3O8粉末，容器為圓柱形，其內徑為70 mm，裝料時鋪平、壓實。測量時，探測器位于物料軸向，距離大于25 cm。各實驗參數列于表1。

3.2 無自吸收時的探測效率

無自吸收的測量條件同3.1節所述，物料填充厚度為1 mm，相應的質量厚度為0.22 g·cm-2，測量后可根據式(5)計算得到235U各特征γ射線的探測效率，結果列于表2。

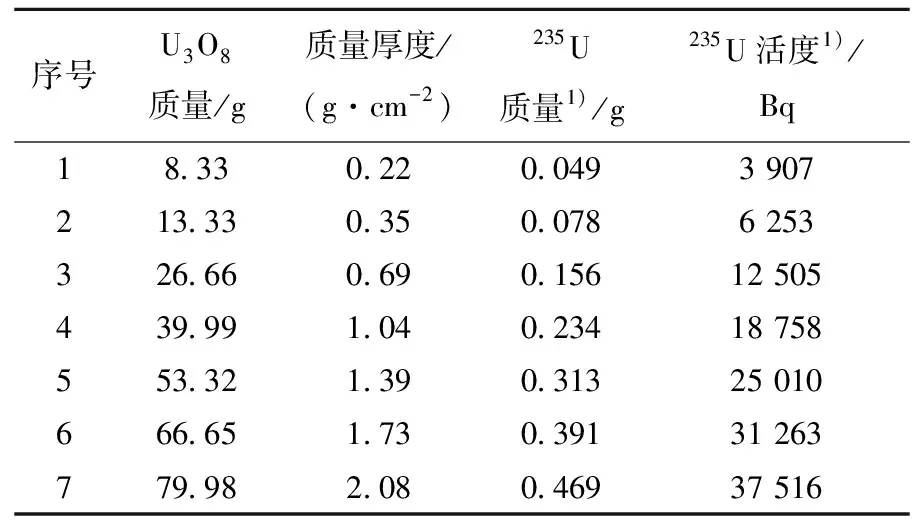
表1 用于系統刻度的U3O8的參數

表2 235U各特征γ射線的探測效率

3.3 自吸收因子比矩陣計算

1) 推算235U比活度

將系統校準所用到的各質量厚度條件下測量得到的235U特征γ射線的計數率推算成235U比活度，結果列于表3。

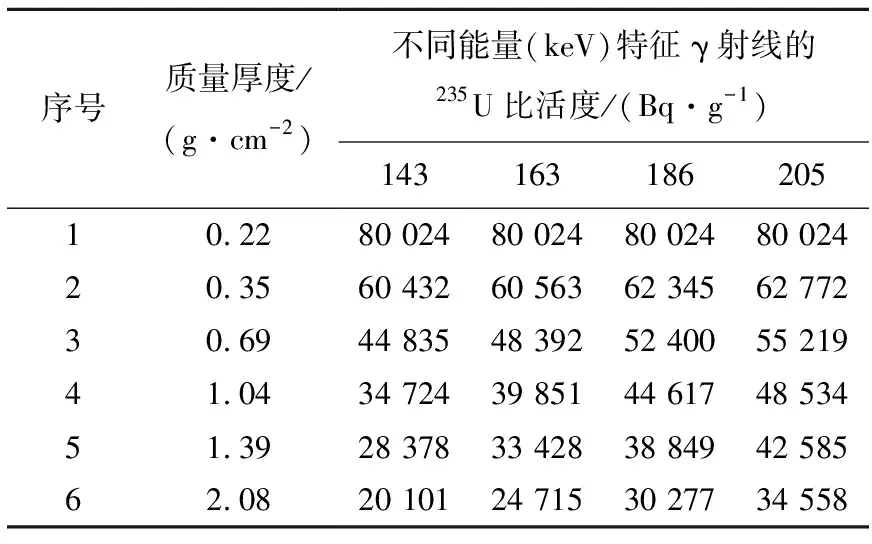
表3 不同質量厚度的235U比活度

從表3可看出，不同質量厚度條件下，由235U特征γ射線的計數率推算所得的235U比活度，隨質量厚度的增加而減小，程度與γ射線能量亦相關。

2) 構建自吸收因子矩陣

以無自吸收條件下的235U比活度作為特定標準，將表3進行轉換，即得系統校準的自吸收因子矩陣，數據列于表4。

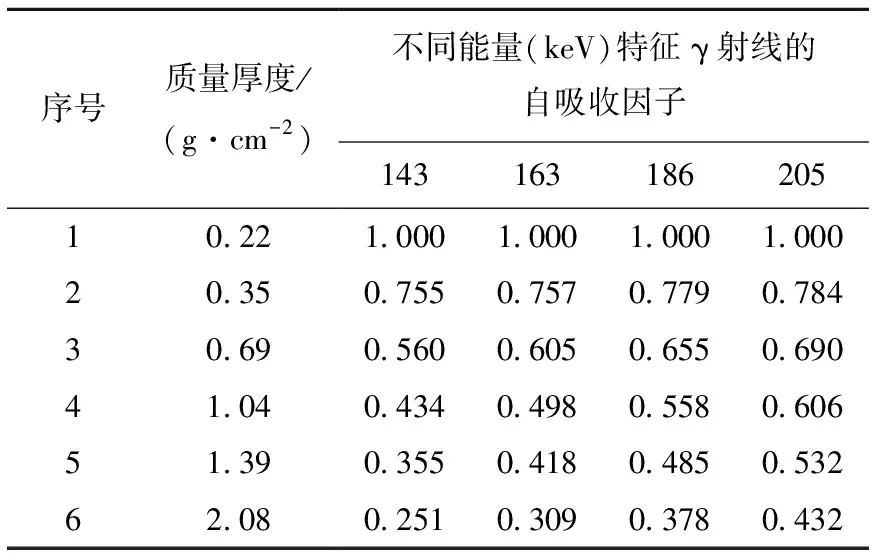
表4 自吸收因子矩陣

依據自吸收因子矩陣，分別取質量厚度和特征γ射線的能量為變量，可擬合得到自吸收縱向變化曲線和橫向變化曲線的系數，本系統校準的縱向變化曲線擬合參數列于表5。

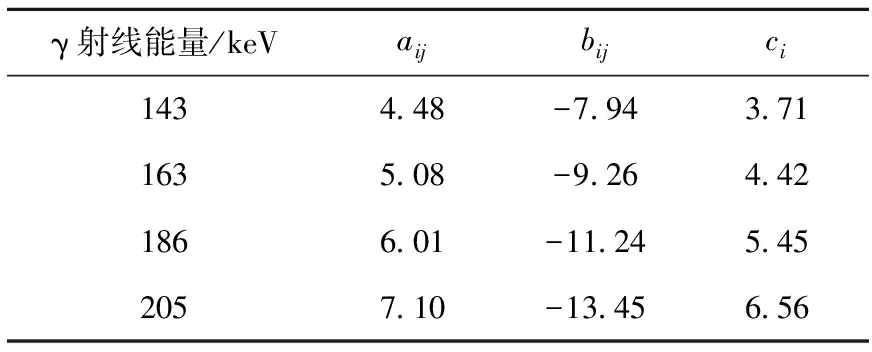
表5 235U自吸收縱向變化曲線擬合參數

4 實驗驗證

取2個樣品進行自吸收校正方法驗證，樣品A質量厚度為1.73 g·cm-2，樣品B接近于飽和厚度，測量條件與系統校準過程保持一致(探測效率見表2)，首先不考慮自吸收影響，應用式(9)計算235U的活度，其中，Gij暫取1，結果列于表6。

(9)

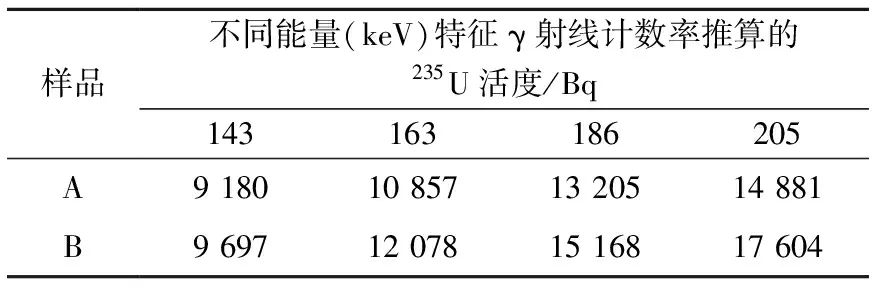
表6 依特征γ射線計數率推算的235U活度

因質量厚度確定的條件下，235U的活度真值必定唯一，將各推算活度與主要γ射線的推算活度相比，即分別得到兩個驗證樣品的一組自吸收因子比，結果列于表7。

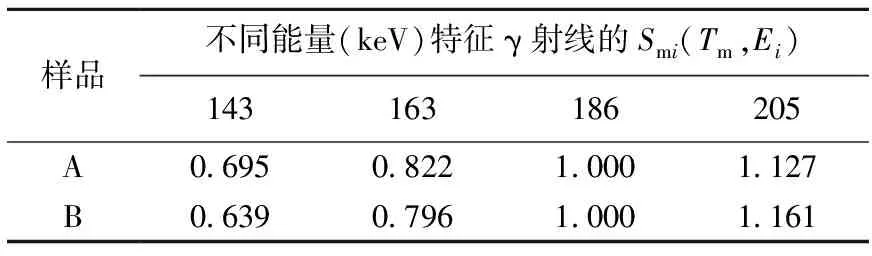
表7 待測樣品的自吸收因子比

將計算結果與系統校準的自吸收因子矩陣對比可得出：樣品A的質量厚度介于1.39 g·cm-2和2.08 g·cm-2之間。故選擇這兩個質量厚度的自吸收因子，代入式(7)進行插值計算，得出該條件下235U各特征γ射線的自吸收因子：Gm,1=0.289，Gm,2=0.356，Gm,4=0.476。通過式(8)計算186 keV的自吸收因子Gm,3=0.425；用同樣方法計算樣品B各特征γ射線的自吸收因子。

此時待解未知量為質量厚度，已知235U各條特征γ射線的自吸收因子，選用縱向變化曲線擬合參數(表5)計算待測物料的質量厚度，結果列于表8。

表8 待測樣品的自吸收因子及質量厚度

5 結語

針對鈾生產工藝設備內滯留量的特點，開展了物料自吸收校正方法的研究，利用某核素多條特征γ射線在物料中自吸收程度不同的特點，通過系統校準，構建了235U特征γ射線自吸收因子矩陣，與射線的能量和不同質量厚度的關系呈現二維特點，因此稱之為自吸收二維修正模型。優點在于避免了常規方法的不確定性，數據處理分析過程簡單可行。

實驗證明，當待測物料的質量厚度未達到各特征γ射線的飽和吸收厚度時，采用此模型推算得到的物料質量厚度相對偏差較小；而當待測物料達到射線的飽和厚度時，計算結果存在較大偏差。另外，若物料的質量厚度非常小，由于各能量γ射線的自吸收不顯著，此條件下進行自吸收效應分析也會帶來較大偏差。

參考文獻：

[1] REILLY D, ENSSLIN N, SMITH H, Jr, et al. Passive nondestructive assay of nuclear materials, NUREG/CR-5550[R]. US: Nuclear Regulatory Commission, 1991.

[2] 陸向東，謝東，田東風. 任意幾何形狀源的γ射線自吸收修正[J]. 核技術，2003，26(10)：759-762.

LU Xiangdong, XIE Dong, TIAN Dongfeng. The γ-ray self-absorption correction for sources with random geometrical shape[J]. Nuclear Techniques, 2003, 26(10): 759-762(in Chinese).

[3] 陸向東，田東風,謝東. 雙層介質核材料的γ特征譜分析[J]. 核技術，2004，27(11)：814-817.

LU Xiangdong, TIAN Dongfeng, XIE Dong. The γ spectra analysis for two-layer nuclear material[J]. Nuclear Techniques, 2004, 27(11): 814-817(in Chinese).

[4] 盧希庭. 原子核物理[M]. 北京：原子能出版社，2001：103.

[5] 復旦大學，清華大學，北京大學. 原子核物理實驗方法[M]. 北京：原子能出版社，1997：65.

[6] THOMAS E S, THOMAS A K. PC/FRAM user manual, LA-UR-99-998[R]. US: LANL, 2001.

[7] 李慶揚，王能超，易大義. 數值分析[M]. 北京：清華大學出版社，2003：23.