快堆MOX燃料氧與金屬原子比控制原理

屈哲昊，尹邦躍，楊啟法，梁雪元

(1.中國原子能科學研究院 反應堆工程研究設計所，北京 102413；

2.核工業標準化研究所，北京 100091)

氧與金屬原子比(O/M比，余同)指MOX燃料即(U1-yPuy)O2±x混合氧化物燃料晶格中氧原子與金屬原子個數的比值，即O/M比=2±x。O/M比是MOX燃料最重要的性能指標之一，對MOX燃料的熔點、晶格常數、理論密度、熱物性、擴散系數、氧在燃料中的化學位即氧勢以及堆內輻照性能均有很大影響。而PuO2含量、Pu分布均勻性、燒結溫度、燒結氣氛氧分壓、粘接劑種類和添加量、批次質量等因素均對O/M比有影響。Toci等[1]指出，富钚顆粒的氧勢一般要高于钚均勻分布的MOX固溶體的氧勢。中國實驗快堆MOX燃料的PuO2質量分數為25%，O/M比為1.96～1.99，如何從理論計算和工藝控制方面達到所要求的O/M比是一個重要的研究課題。

國外從20世紀50年代開始研究核燃料的氧勢和O/M比，現已得到數千個數據，但這些數據通常是在有限的“氧勢-溫度-成分”范圍內重復進行，由于實驗測量條件不同，數據分散性較大。各國也提出了很多氧勢理論模型，但由于采用不同的離子平衡假設和不同的熱力學數據，計算結果與實驗數據存在較大差異，至今沒有一個普遍公認的氧勢模型[2-7]。根據經驗，在MOX燃料芯塊生產過程中，一般通過控制燒結氣氛的氧分壓即氣體氧勢來調整固體芯塊的氧勢和O/M比。顯然，了解MOX燃料的O/M比控制原理將有利于優化MOX燃料芯塊的燒結工藝參數，本文將進行MOX燃料的O/M比控制原理的研究。

1 氧勢模型

氧化物陶瓷芯塊在保溫燒結過程中，固體芯塊內的氧勢與燒結氣氛的氧勢存在平衡，根據熱力學定律，氧化學位為：

(1)

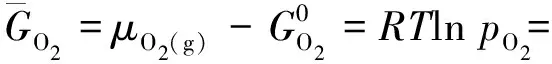
(2)

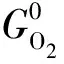
MOX芯塊的O/M比是固體內的化學位即氧勢、溫度和Pu含量的函數，為建立O/M比與MOX燃料芯塊燒結工藝(燒結溫度、氧分壓和PuO2含量)之間的關系，需通過熱力學參數或離子反應平衡常數精確計算氧勢，并建立O/M比與氧勢之間的關系式。國外早在20世紀50年代就已開始進行核燃料的氧勢研究，從晶體結構缺陷、熱力學行為角度出發，發展了燃料的多種氧勢熱力學理論和數學模型[8]。公認的氧勢模型主要有Rand-Markin模型、Blackburn模型、相平衡模型、點缺陷模型。這些理論模型采用了一些假設和有差異的熱力學數據，測量數據由于原理或技術的原因存在誤差，使氧勢模型的應用有限。

1) Rand-Markin價態模型

Rand-Markin模型是基于實驗結果的經驗模型，它把MOX視為UO2+x與PuO2-x形成的理想固溶體(U1-yPuy)O2±x。該模型假設：當MOX芯塊為超化學計量時，即(U1-yPuy)-O2+x的O/M比大于2.00時，氧勢為鈾平均價態的函數；當其為亞化學計量時，即(U1-yPuy)-O2-x的O/M比小于2.00時，氧勢為钚平均價態的函數，且不受溫度和Pu/U比的影響[9]。

對于亞化學計量(U1-yPuy)O2-x而言，U離子的價態VU是+4，但Pu離子的平均價態VPu不是整數。

VPu=4-2x/y

(3)

對于超化學計量(U1-yPuy)O2+x而言，Pu離子的價態為+4，但U離子的平均價態不是整數：

VU=4+2x/(1-y)

(4)

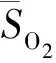
2) Blackburn離子平衡模型

Blackburn模型[12]可認為是半經驗性模型，它認為MOX固溶體中存在確定的U、Pu離子價態，各價態離子相互平衡，構成一系列平衡方程。MOX燃料通常在強還原性氣氛中進行燒結，離子平衡反應要考慮U2+-U4+、U4+-U6+、Pu3+-Pu4+、Pu2+-Pu3+等反應體系，其對應的反應平衡常數分別為：

(5)

(6)

(7)

(8)

式中，[U2+]、[U4+]、[U6+]、[Pu2+]、[Pu3+]、[Pu4+]、[O2-]分別為U2+、U4+、U6+、Pu2+、Pu3+、Pu4+、O2-的濃度，余同。

對于確定成分與O/M比的(U1-yPuy)O2±x燃料，x和y是已知量，有：

[U2+]+[U4+]+[U6+]=1-y

(9)

[Pu2+]+[Pu3+]+[Pu4+]=y

(10)

2[U2+]+4[U4+]+6[U6+]+2[Pu2+]+

3[Pu3+]+4[Pu4+]=2±x=2[O2-]

(11)

當反應平衡常數已知，聯立解上述7個公式即可求得pO2；或當pO2和y已知，同樣可根據式(5)～(8)求解x，從而得到混合氧化物燃料的O/M比。圖1為利用Blackburn模型計算得到的MOX燃料氧勢與O/M比的關系[13]。

Blackburn模型計算過程較簡單，方法易掌握，計算量少，精確度受反應平衡常數的影響較大。Blackburn發布模型時，利用相圖中UO2/U4O9、UO2-x/U(l)平衡數據分別計算得到了KU24、KU46。也可利用已知的pO2、x、y等數據，擬合得到平衡常數。受Stan等[11,14]的啟發，若結合量子力學理論與分子動力學計算技術進行反應平衡常數的理論估算，再利用實驗數據進行修正，可得到更準確的反應平衡常數，從而提高Blackburn模型的計算準確度。

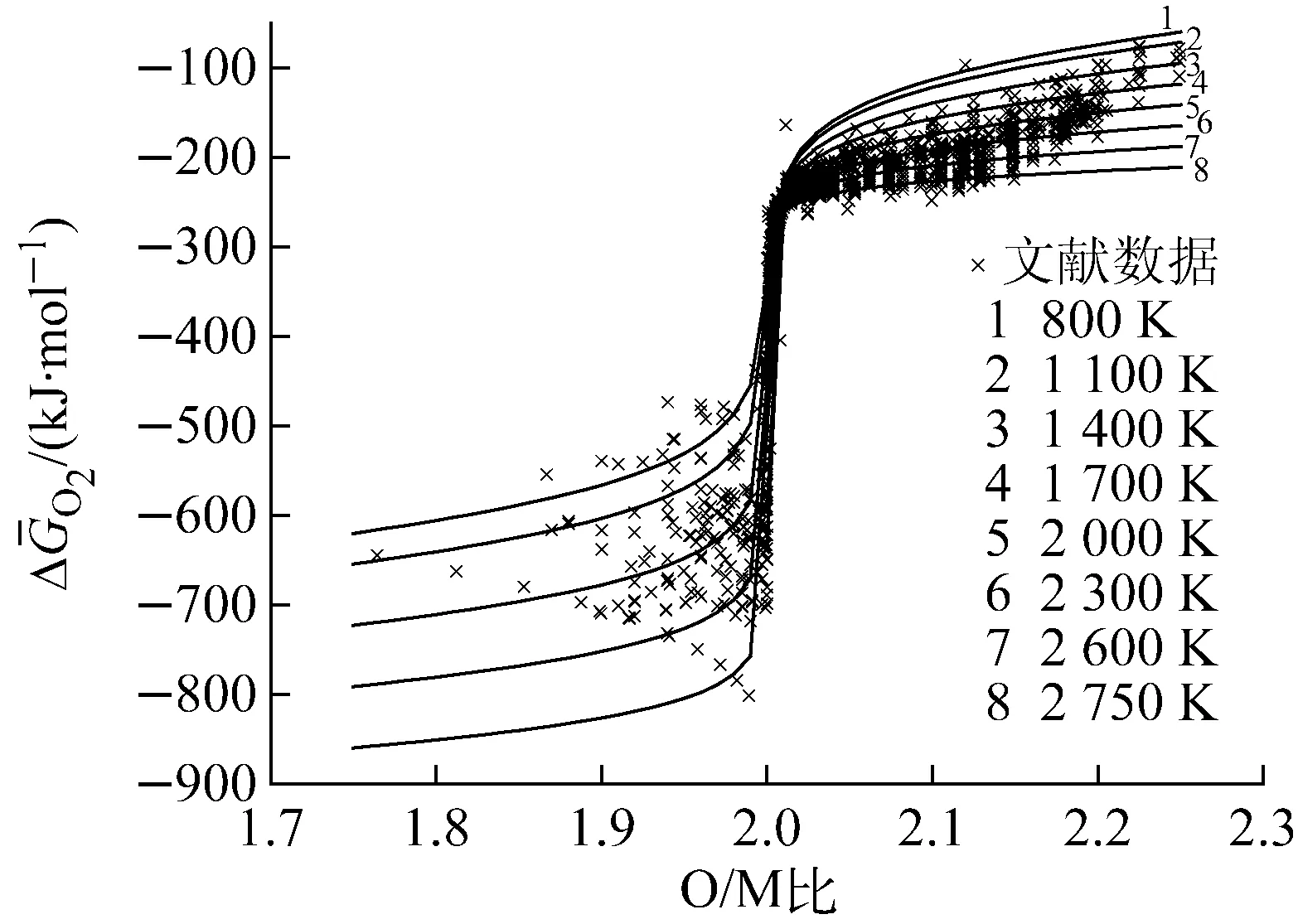
圖1 Blackburn模型計算得到的MOX燃料的氧勢與O/M比的關系[13]

3) 相平衡模型

相平衡模型假定MOX燃料中U4O9與UO2、Pu2O3與PuO2之間存在相互平衡，且U4O9、Pu2O3這兩種含非化學計量缺陷的化合物可對應地溶解于無缺陷的化學計量比化合物UO2、PuO2中。

8UO2+O2(g)=2U4O9

2Pu2O3+O2(g)=4PuO2

形成(U1-yPuy)Ox固溶體的標準吉布斯自由能為：

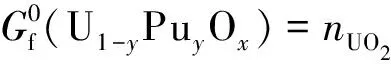
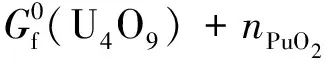
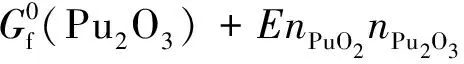
(12)

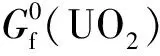
相平衡模型是Hoch等[15]在錒系氧化物中采用的模型，Besmann等[16-17]和Krishnaiah[18]將其應用于MOX燃料。目前很少采用該方法計算MOX燃料的氧勢，僅Varamban等[19]利用此方法預測MOX燃料的氧勢。

4) 點缺陷模型

由于非化學計量化學物中必然存在間隙離子、空位、自由電子、電子空隙等結構缺陷，它們之間也會構成平衡，因此點缺陷模型認為可通過計算缺陷平衡反應來得到固溶體的氧勢。

MOX燃料可能存在以下缺陷反應(使用Kroger-Vink符號表示缺陷)：

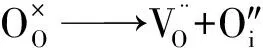
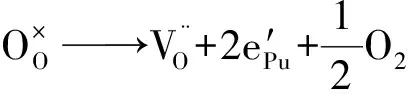
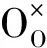
假設上述6個反應平衡常數已知，則可通過計算MOX固溶體的氧空位與氧間隙原子濃度計算O/M比：

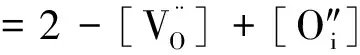
(13)

利用點缺陷模型求解MOX燃料氧勢的計算結果與實驗結果符合較好，此方法被Kato等[20-21]廣泛應用于MOX燃料和嬗變燃料的研究中。但目前尚無文獻報道如何通過理論計算得到平衡常數。Kato等[22]利用實際測量的氧勢擬合計算得到U0.8Pu0.2O2±x的各平衡常數如下：

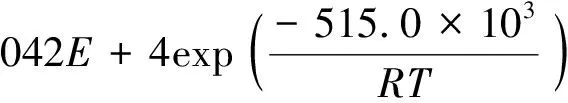
(14)

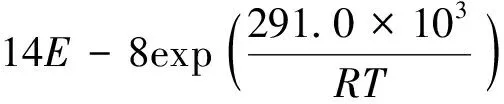
(15)

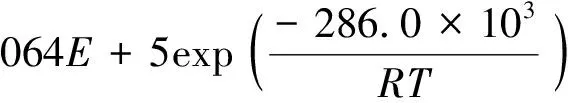
(16)

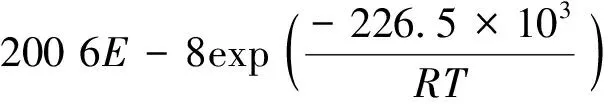
(17)

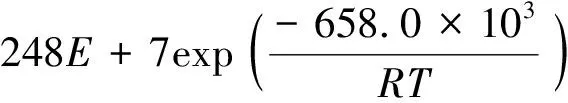
(18)

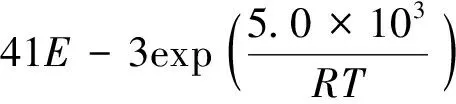
(19)

Blackburn模型和點缺陷模型是目前應用最多的兩種理論模型，并已積累了大量實驗數據。利用國外現有離子反應平衡常數和熱力學數據，采用Blackburn模型可精確研究MOX燃料的氧勢，但目前這些數據較少，今后應開展更為精確的點缺陷模型計算研究。

2 MOX燃料O/M比控制工藝計算

2.1 氧分壓計算

為使MOX燃料的O/M比達到指標設計要求，要根據氧勢模型計算出氧勢的控制范圍，再根據氧勢精確計算結果計算在某燒結溫度下的氧分壓，最后根據氧分壓控制氣體露點。

假設快堆MOX燃料芯塊的設計成分分別為(U0.7Pu0.3)O2-x、(U0.75Pu0.25)O2-x、(U0.8Pu0.2)O2-x，分別利用Blackburn模型和點缺陷模型計算得到不同O/M比對應的氧分壓，結果分別列于表1和2。采用Blackburn模型進行計算，對于(U0.7Pu0.3)O2-x燃料，當設計O/M比為1.97時，若在1 700 ℃、Ar-5%H2氣中燒結，則要求將氧分壓控制為7.70×10-6Pa，或將氧勢控制為-381.98 kJ/mol。對于(U0.75Pu0.25)O2-x燃料，當設計O/M比為1.97時，若在1 700 ℃、Ar-5%H2氣中燒結，則要求將氧分壓控制為3.05×10-6Pa，或將氧勢控制為-397.18 kJ/mol。可見，要達到相同的亞化學計量O/M比，PuO2含量高則對燒結氣氛的氧分壓控制要求可適當放松。

采用點缺陷模型計算得到了MOX燃料的燒結氣氛氧分壓，對于(U0.7Pu0.3)O2-x燃料，當設計O/M比為1.97時，如果在1 700 ℃、Ar-5%H2氣中燒結，則要求將氧分壓控制在3.52×10-6Pa(而Blackburn模型計算值為7.70×10-6Pa)，或將氧勢控制在-394.87 kJ/mol。對于(U0.75Pu0.25)O2-x燃料，當設計O/M比為1.97時，如果在1 700 ℃、Ar-5%H2氣中燒結，則要求將氧分壓控制在1.23×10-6Pa(而Blackburn模型計算值為3.05×10-6Pa)，或將氧勢控制在-412.11 kJ/mol。

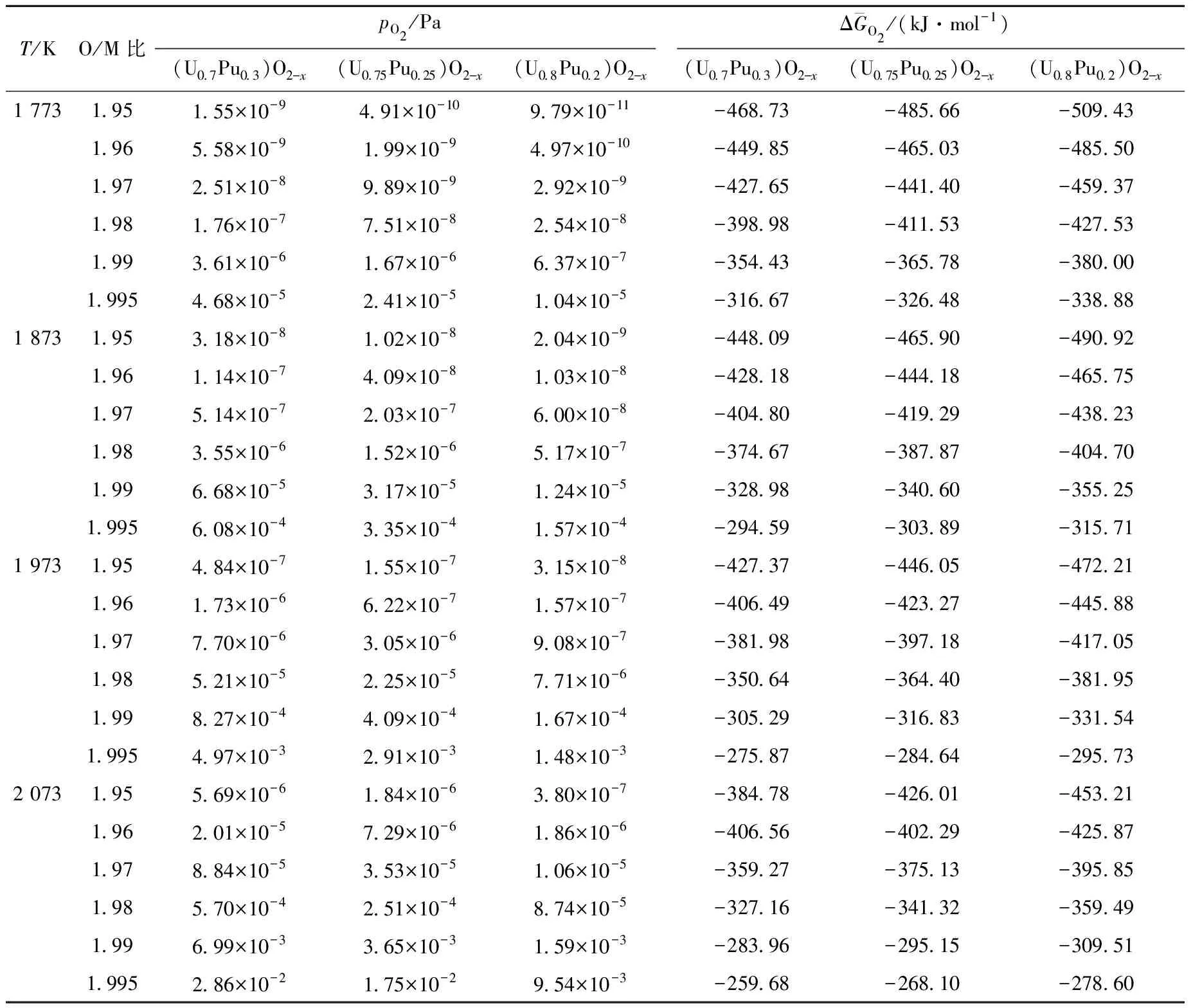
表1 Blackburn模型計算得到的燒結氣氛的氧分壓和氧勢

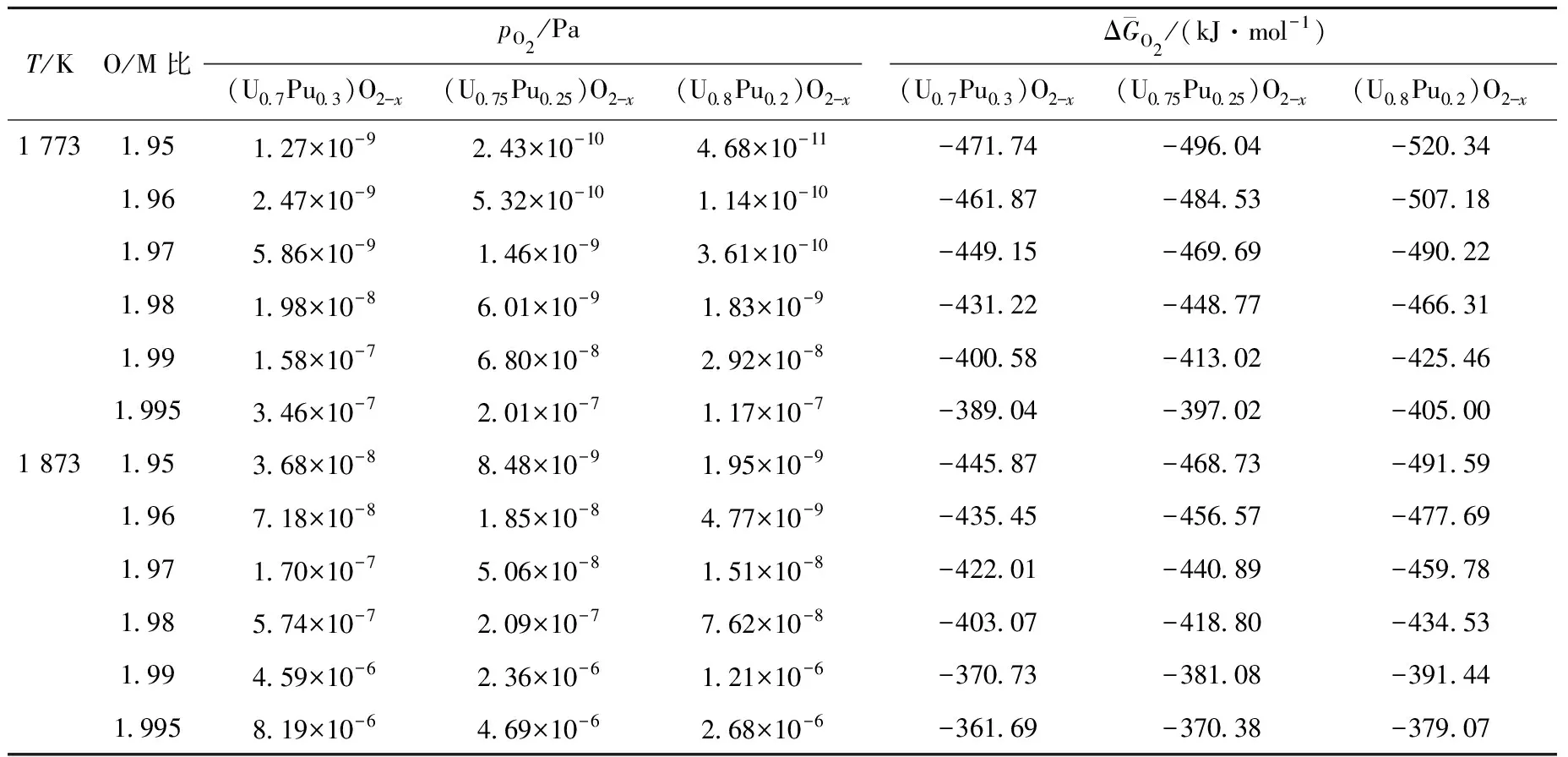
表2 點缺陷模型計算得到的燒結氣氛的氧分壓和氧勢

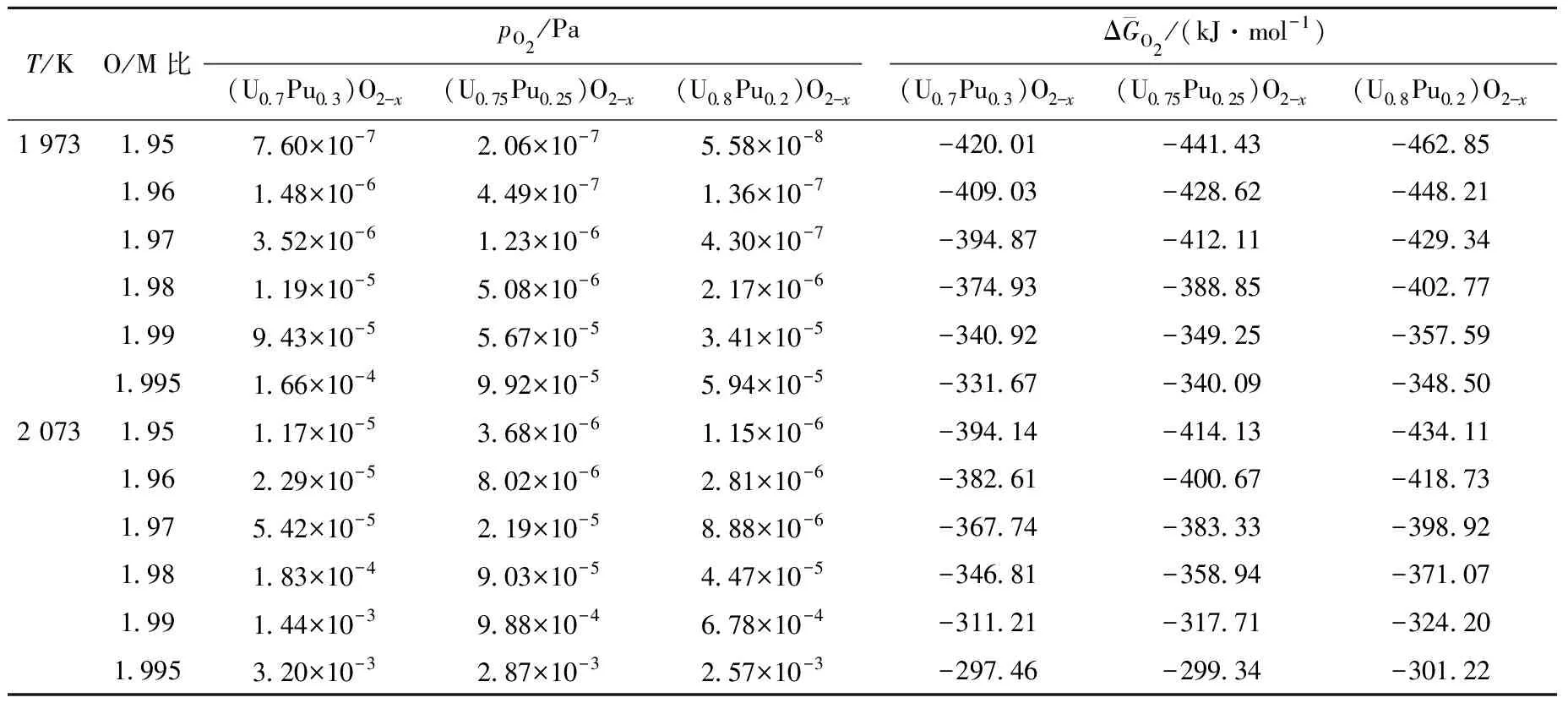
續表2

比較Blackburn模型與點缺陷模型的計算結果可發現，兩種模型的計算結果變化規律基本一致(圖2)，但Blackburn模型的氧勢和氧分壓隨O/M比增大而增大的速度較快。圖2顯示，當O/M比≤1.96時，Blackburn模型的氧勢和氧分壓計算結果均相應地低于點缺陷模型的；而當O/M比>1.96時，Blackburn模型的氧勢和氧分壓計算結果均相應地高于點缺陷模型的。今后應根據自有實驗數據選擇合適模型以用于理論預測我國MOX芯塊燒結氣氛氧分壓。由于目前文獻報道的點缺陷模型平衡常數有限，盡管國外研究者認為其與實驗符合較好，但在本文后續計算中仍選用Blackburn模型計算數據。

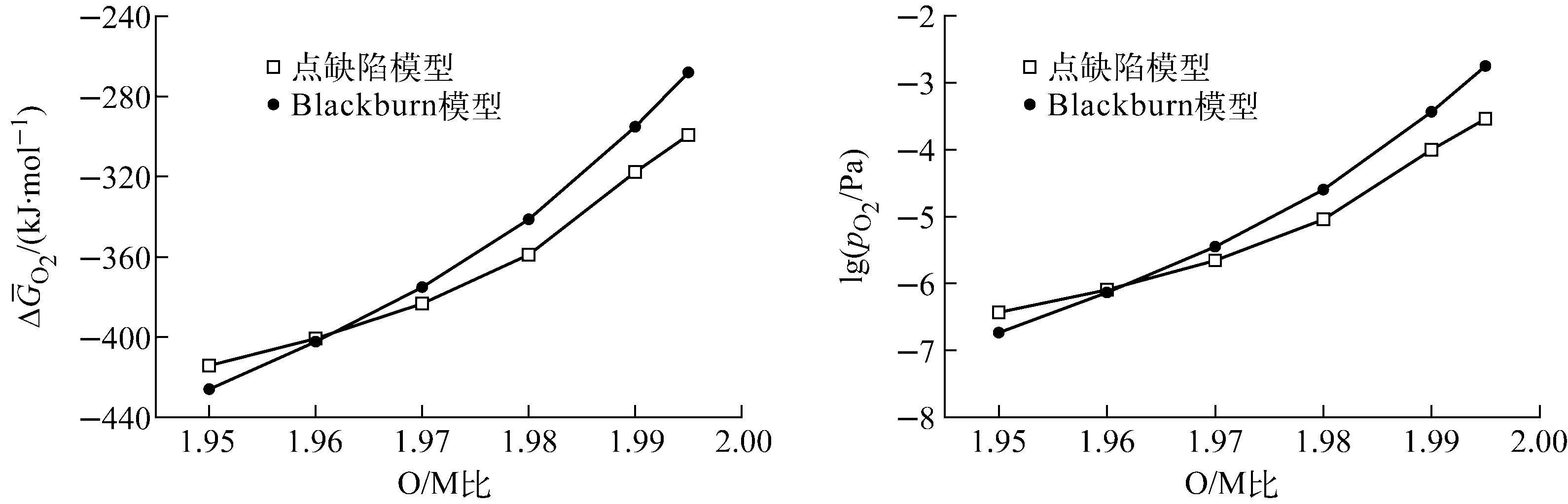
圖2 Blackburn模型與點缺陷模型計算結果的比較

2.2 露點計算

如果燒結氣氛中存在水，存在2H2+O2→2H2O反應，則：

(20)

式中：p為各氣態物質的分壓；Keq為該反應平衡常數，有：

(21)

ΔG0=ΔH0-TΔS0=-492 880+109.6T

(22)

pH2/pH2O=

(23)

根據Blackburn模型計算結果，以(U0.75-Pu0.25)O1.97為例進行計算分析，1 700 ℃燒結時要求將氧分壓控制在3.05×10-6Pa，于是計算得到：

pH2/pH2O=

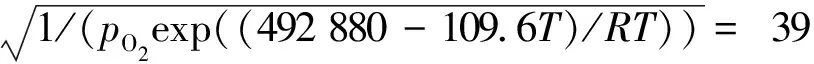
若pH2=0.1 MPa，則pH2O=2 529.08 Pa。實際MOX芯塊燒結氣氛為Ar-5%H2混合氣體，若混合氣體的壓力為0.1 MPa，pH2=5 kPa，則pH2O=126.45 Pa，即混合氣體中的水分含量應控制為1 264.5 ppm。

通過冷凝器冰浴[23]可調節氣體pH2/pH2O，對于冰面體系，飽和水蒸氣壓與溫度的關系可通過以下方程計算：

lnpH2O=-6 024.528 2T-1+29.327 07+

1.061 386 8×10-2T-1.319 882 5×

10-5T2-0.493 825 77lnT

(24)

通過式(23)計算得到pH2O后，求解式(24)即可得到冷凝器的工作溫度即露點T為291.58 K(18.58 ℃)。可見，將露點為18.58 ℃的0.1 MPa純H2氣或水分含量為1 264.5 ppm、露點為255.28 K(-17.72 ℃)的0.1 MPa Ar-5%H2混合氣通過冷凝器冰浴脫水后，再通入燒結爐內在1 700 ℃燒結，理論上可得到成分為(U0.75Pu0.25)O1.97的MOX芯塊。若燒結溫度提高至1 750 ℃，要使(U0.75Pu0.25)O2-x的O/M比控制在1.97，則要求將0.1 MPa Ar-5%H2氣體的水分含量控制在1 633.7 ppm、露點控制在258.02 K(-14.98 ℃)。

采用上述同樣方法可計算得到1 750 ℃燒結具有不同成分和O/M比的(U0.75Pu0.25)O1.95、(U0.75Pu0.25)O1.96、(U0.75Pu0.25)O1.98、(U0.75Pu0.25)-O1.99、(U0.75Pu0.25)O1.995芯塊時，必須將0.1 MPa Ar-5%H2氣體的水分含量分別控制在370.4、739.8、4 403.6、17 855.4、43 064.8 ppm，露點分別控制在-30.10、-23.27、-3.77、13.83、26.16 ℃(圖3)。其他成分MOX燃料的燒結氣體水分含量和露點計算結果列于表3。

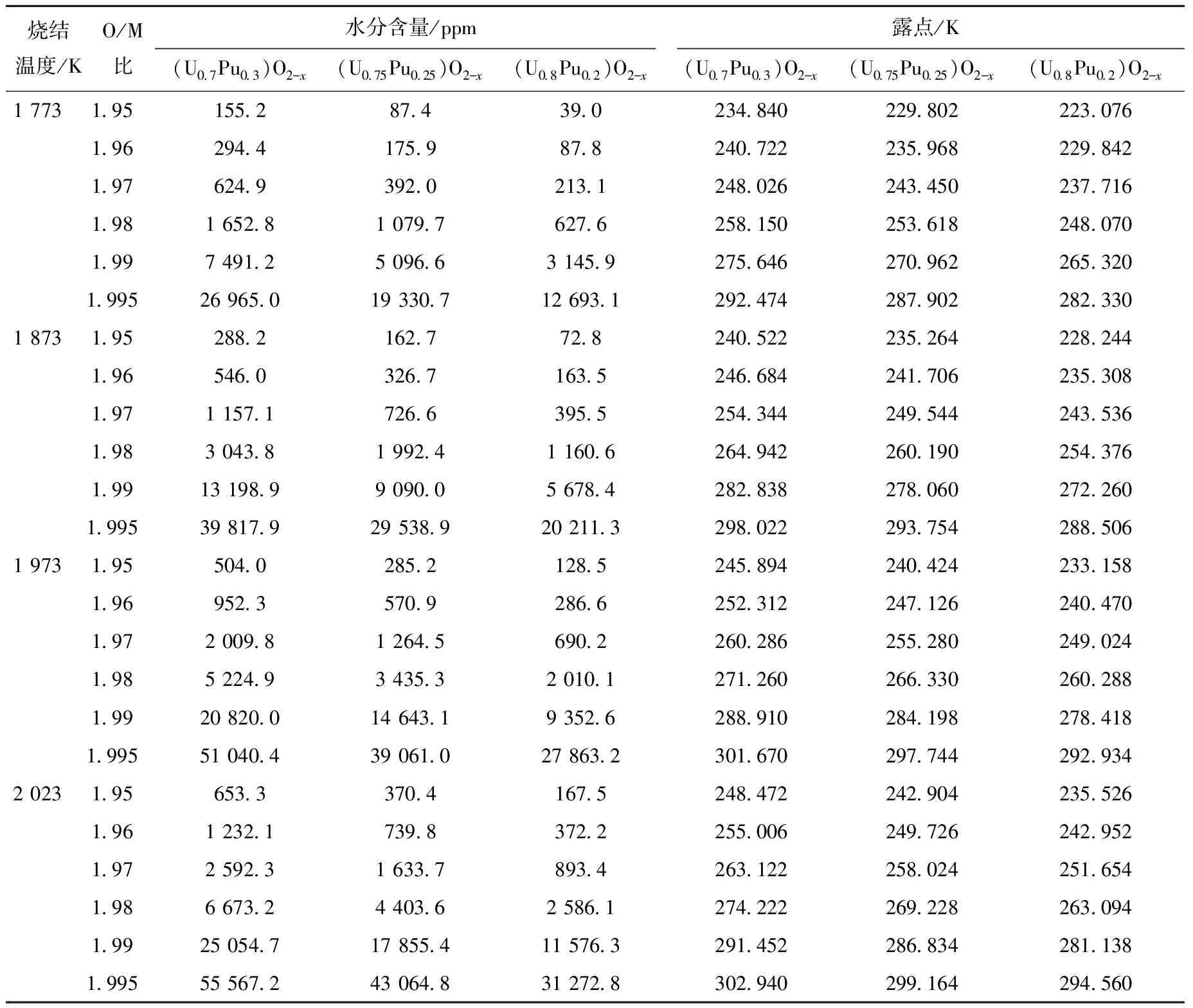
表3 MOX芯塊燒結氣氛中水分含量及露點

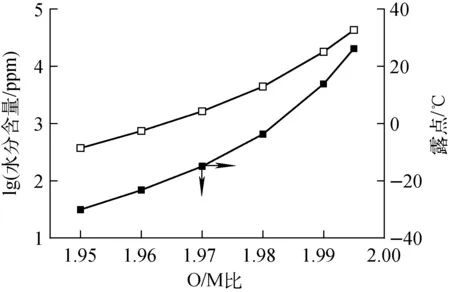
圖3 (U0.75Pu0.25)O2-x的O/M比與燒結氣體水分含量和露點的關系

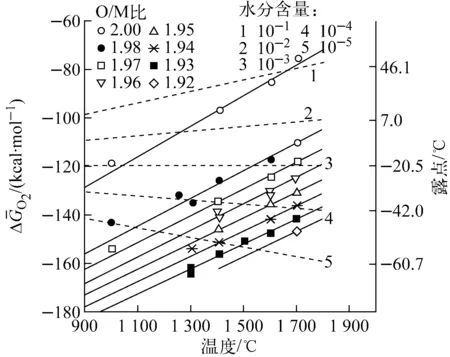
圖4 氧勢、燒結溫度、氣體水分含量和露點對(U0.8Pu0.2)O2-x燃料O/M比的影響[24]

圖4所示為美國阿貢國家實驗室的(U0.8Pu0.2)O2-x燃料的O/M比與氧勢、溫度和氣體露點的關系[24]。可見，若要求O/M=1.97，在1 700 ℃燒結時氣體的氧勢應控制在約-420 kJ/mol，較本文計算的氧勢偏低(Blackburn模型計算的氧勢為-397.18 kJ/mol，點缺陷模型的為-412.11 kJ/mol)，露點約為-20 ℃。本文計算得到(U0.8Pu0.2)O1.97燃料在1 700 ℃燒結時，要求控制氣體水分含量為690.2 ppm、露點為-23.98 ℃；在1 750 ℃燒結時，要求控制氣體水分含量為893.4 ppm、露點為-21.35 ℃，這與文獻[24]的結論基本一致。俄羅斯專家指出快堆MOX芯塊在1 750 ℃、Ar-8%H2氣中燒結，當H2氣中H2O含量分別為0.03%、0.3%時，即氣體露點分別為-40、-16 ℃時，對應O/M比可分別達到1.95、1.98，但其MOX燃料的PuO2含量未知。本文計算得到(U0.75Pu0.25)O1.95、(U0.75Pu0.25)O1.98燃料分別在1 750 ℃、Ar-8%H2氣中燒結時，要求控制氣體露點分別為-32.34、-6.5 ℃，比俄羅斯專家提出的露點均高約8 ℃。

3 結論

1) Blackburn模型和點缺陷模型是兩種常用的核燃料氧勢模型，離子反應平衡常數和熱力學數據是影響氧勢模型精確度的主要因素。采用精確的平衡常數和熱力學數據，以及大量實測數據對氧勢模型進行修正，可提高氧勢計算和O/M比預測的精確度。

2) 在PuO2含量和燒結溫度一定的情況下，MOX芯塊的O/M比可通過控制氣相中氧分壓或露點來調整。將保護氣體通過冷凝器冰浴脫水后再進入燒結爐內，可定量調節氣體氧勢和精確控制芯塊的O/M比。

3) 當要求(U0.75Pu0.25)O2-x燃料的O/M比為1.97時，若在1 750 ℃、0.1 MPa Ar-5%H2氣中燒結，采用Blackburn模型進行計算，則理論上要求將氧分壓控制在1.07×10-5Pa，或將氧勢控制在-386.15 kJ/mol。采用點缺陷模型計算，要求將氧分壓控制在0.7×10-5Pa，或將氧勢控制在-393.22 kJ/mol。

4) (U0.75Pu0.25)O2-x燃料在1 750 ℃、0.1 MPa Ar-5%H2氣中燒結，當要求O/M比分別為1.95、1.96、1.97、1.98、1.99、1.995時，理論上應將氣體中的水分含量分別控制在370.4、739.8、16 33.7、4 403.6、17 855.4、43 064.8 ppm，或將氣體露點分別控制在-30.10、-23.27、-14.98、-3.77、13.83、26.16 ℃。

參考文獻：

[1] TOCI F, MANES L, EWART F T, et al. On the determination of oxygen potentials and O/M ratios in mixed U-Pu oxides by means of solid state galvanic cells[J]. Journal of Applied Electrochemistry, 1979, 9(3): 399-401.

[2] KUTTY T R G, HEGDE P V, KAHN K B, et al. Densification behavior of UO2in six different atmospheres[J]. Journal of Nuclear Materials, 2002, 305(2-3): 159-168.

[3] LAY K W, CARTER B E. Role of the O/U ratio on the sintering of UO2[J]. Journal of Nuclear Materials, 1969, 30(1-2): 74-87.

[4] HARADA Y. UO2sintering in controlled oxygen atmospheres of three-stage process[J]. Journal of Nuclear Materials, 1997, 245(2-3): 217-223.

[5] CHEVREL H, DEHAUDT P, FRANCOIS B, et al. Influence of surface phenomena during sintering of over stoichiometric uranium dioxide UO2+x[J]. Journal of Nuclear Materials, 1992, 189(2): 175-182.

[6] ASSMANN H, DOERR W, PEEHS M. Oxide fuels with controlled microstructure[J]. Journal of the American Ceramic Society, 1984, 67(9): 631-636.

[7] FUHRMAN N, HOWER L D, HOLDEN R B. Low-temperature sintering of uranium dioxide[J]. Journal of the American Ceramic Society, 1963, 46(3): 114-121.

[8] 唐納德·奧蘭德. 核反應堆燃料元件基本問題[M]. 北京：原子能出版社，1983：231.

[9] RAND M H, MARKIN T L. Some thermodynamic aspects of (U, Pu)O2solid solutions and their use as nuclear fuels[C]∥Thermodynamics of Nuclear Materials 1967 Symposium Proceedings. Vienna: [s. n.], 1968: 637-650.

[10] FUJINO T, SATO N, YAMADA K. A refined analysis of oxygen potential of MyU1-yO2+x(M=M3+and M2+) by lattice statistics based on the grand partition function and the Flory methods[J]. Journal of Nuclear Materials, 1995, 223(1): 6-19.

[11] STAN M, CRISTEA P, Sr WALLACE T C. Thermochemistry of defects and oxygen diffusion in PuO2-x[C]∥Proceedings of 11th Symposium on Thermodynamics of Nuclear Materials. Karlsruhe, Germany: [s. n.], 2004.

[12] BLACKBURN P E, JOHNSON C E. Oxygen pressures over fast breeder reactor fuel (Ⅰ): A model for UO2±x[J]. Journal of Nuclear Materials, 1973, 46(3): 244-252.

[13] 梁雪元. MOX燃料混合工藝及熱力學分析[D]. 北京：中國原子能科學研究院，2006.

[14] STAN M. Theory-based models and simulations of materials for fusion[C]∥Fusion Power Renew Workshop. US: University of California, 2009.

[15] HOCH M, FURMAN F J. Non-stoichiometry of UO2-CeO2: The system UO2-CeO2-CeO1.5at 900 to 1 200 ℃[C]∥Thermodynamics Proceedings of the Symposiumn on Thermodynamics With Emphasis on Nuclear Materials and Atomic Transport in Solids. Vienna: IAEA, 1966: 517-532.

[16] BESMANN T M, LINDEMER T B. Chemical thermodynamic representation of UO2±x[C]∥ Proceedings of Conference on Thermodynamics. Hamilton, Canada: [s. n.], 1984.

[17] BESMANN T M, LINDEMER T B. Chemical thermodynamic representation of PuO2-xand U1-zPuzOw[C]∥ Proceedings of Conference on Chemical Thermodynamics and 39 Calorimetry Conference. Hamilton, Canada: [s. n.], 1984.

[18] KRISHINAIAH M V, SRIRAMAMURTI P. Computational model for the oxygen potentials of mixed uranium-plutonium oxide[J]. Journal of the American Ceramic Society, 1984, 67(8): 568-571.

[19] VANA VARAMBAN S, GANESAN V, VASUDEVA RAO P R. Estimation of oxygen potential for U-Pu-O mixed oxide fuel[J]. Journal of Nuclear Materials, 2009, 389(1): 72-77.

[20] KATO M, NAKAMICHI S, TAKEUCHI K, et al. Measurement of oxygen potential of (U0.8-Pu0.2)O2±xat 1 773 and 1 873 K, and its analysis based on point defect chemistry[J]. CALPHAD, 2011, 35(4): 623-626.

[21] KATO M, KONASHI K, NAKAE N. Analysis of oxygen potential of (U0.7Pu0.3)O2±xand (U0.8-Pu0.2)O2±xbased on point defect chemistry[J]. Journal of Nuclear Materials, 2009, 389(1): 164-169.

[22] KATO M. Oxygen potentials and defect chemistry in nonstoichiometric (U, Pu)O2[R]∥Stoichiometry and Materials Science: When Numbers Matter. [S. l.]: [s. n.], 2012: 203-218.

[23] RASMUSSEN D E, BENECKE M W, JENTZEN W R, et al. Oxygen to metal ratio control during fabrication of mixed oxide fast breeder reactor fuel pellets, HEDL-SA-1763FP[R]. Atlanta: Hanford Engineering Development Laboratory, 1979.

[24] JAVED N A. Thermodynamic behavior of (U, Pu) mixed-oxide fuels[J]. Journal of Nuclear Materials, 1973, 47(3): 336-344.