基于偽降階磁鏈觀測器的速度辨識方法

柳 巍， 阮 毅， 吳曉新， 張笠君

(上海大學 機電工程與自動化學院，上海 200072)

0 引 言

磁場定向控制的概念被廣泛應用于高性能感應電機控制。在感應電機驅動系統(tǒng)中，為了獲得速度信息，需要一個速度傳感器，如測速發(fā)電機、旋轉變壓器、數字位置編碼器等。在交流傳動領域，已提出基于磁場定向的無速度傳感器方案，主要通過軟件算法代替硬件得到電機速度[1- 4]。

文獻[3]和文獻[4]提出了一種自適應全階磁鏈觀測器方案，用于估計轉子磁通和電機速度。速度自適應率主要是采用Popov和Lyapunov穩(wěn)定性方法來實現。由于全階磁鏈觀測器的反饋增益矩陣與電機的運行速度有關，實現比較復雜。如果采用開環(huán)的全階磁鏈觀測器，即增益矩陣設置為零，則電機在低速情況下會出現不穩(wěn)定的現象，在重載情況下會出現較大的速度誤差[5]。文獻[5]提出了一種基于自適應偽降階磁鏈觀測器的速度辨識方法，利用Lyapunov方法進行速度辨識，在中、高速范圍，偽降階磁鏈觀測器的性能相比全階磁鏈觀測器有了一定的改善。Lyapunov方法需要確定適當的Lyapunov函數，該函數的確定非常困難。文獻[6]利用Popov方法代替Lyapunov方法用于速度辨識。由于文獻[5]和文獻[6]都是在觀測磁鏈和實際磁鏈相等的假設條件下，得到觀測器的極點與電機轉速無關，所以系統(tǒng)的穩(wěn)定性還有待進一步研究。

本文研究了一種自適應偽降階磁鏈觀測器，反饋增益矩陣設計簡單，與電機轉速無關。比常見的全階磁鏈觀測器簡單，因此需要的計算時間更少，有利于數字實現。對該方法進行了仿真和試驗驗證，從低速到高速范圍，電機都能穩(wěn)定運行，克服了低速不穩(wěn)定的問題，證明了該方法的有效性。

1 異步電機及偽降階觀測器模型

在兩相靜止坐標系，將定子電流和轉子磁鏈作為狀態(tài)變量，則異步電機模型的狀態(tài)方程可表示為

(1)

(2)

式中：ωr——轉速；

τr——轉子時間常數；

Lm——互感；

Ls、Lr——定、轉子電感；

σ——漏感系數；

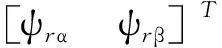
將定子電流觀測誤差ei作為反饋量，則偽降階自適應觀測器如圖1所示。ei通過誤差反饋增益矩陣G構成漸進狀態(tài)觀測器，并通過自適應機制對轉速進行估計。以is和ψr為狀態(tài)變量構建的異步電機偽降階閉環(huán)觀測器可表示為

(3)

(4)

式中： G——反饋增益矩陣，G的值為了確保觀測器的穩(wěn)定性。

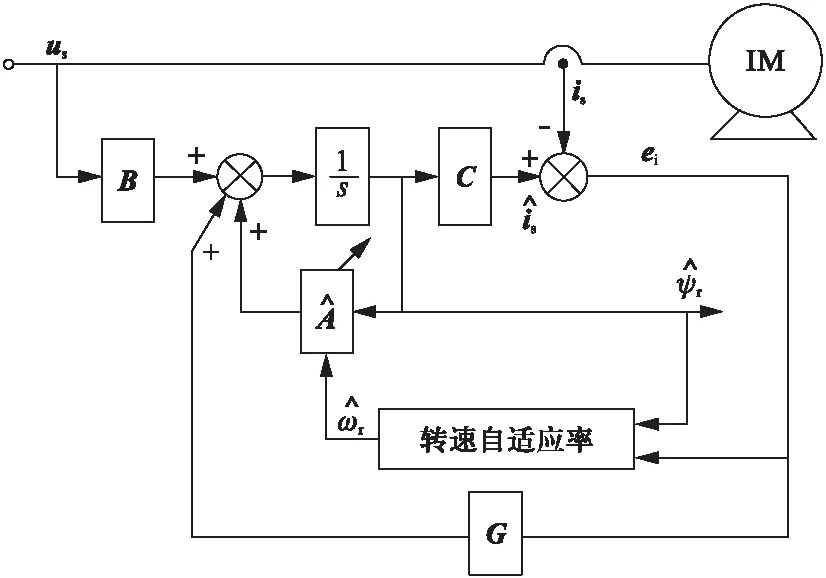
圖1 偽降階自適應觀測器

2 速度辨識及反饋矩陣設計

2.1 速度辨識

式(3)和式(4)中，如果將轉速認為是變化的參數，將電機模型減去觀測器模型，可以得到靜止坐標系下的狀態(tài)觀測誤差方程

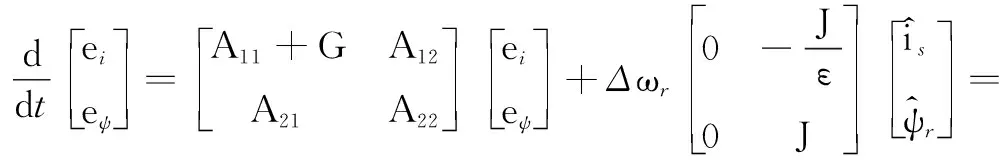
(5)

根據式(5)，誤差方程可以等價為非線性反饋系統(tǒng)。該系統(tǒng)由一個線性定常前向通道和一個非線性時變反饋通道組成，狀態(tài)觀測誤差框圖如圖2所示。

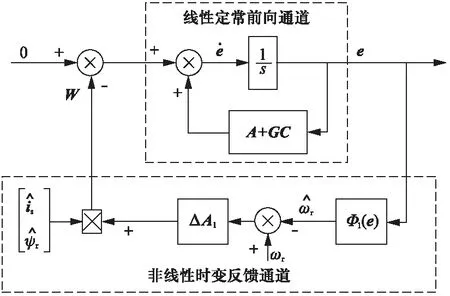
圖2 狀態(tài)觀測誤差框圖

圖2中，Φ1(e)是轉子轉速的自適應辨識函數。根據Popov超穩(wěn)定性理論，一個由線性前向通道和一個非線性時變反饋通道組成的系統(tǒng)，如果其非線性反饋部分滿足Popov不等式，那么該系統(tǒng)處于漸進穩(wěn)定的充分必要條件是線性前向通道的傳遞函數嚴格正實。假設圖2中線性定常前向通道為嚴格正實，只要選取適當的自適應律，使非線性反饋部分滿足Popov不等式(6)，即可保證系統(tǒng)漸進穩(wěn)定。

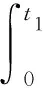
(6)

文獻[4]給出了詳細證明，如果電機轉速辨識滿足式(7)，則滿足Popov不等式。

(7)

式中：Kp、Ki——比例、積分系數。

2.2 反饋矩陣設計

PI自適應律可以保證非線性反饋部分滿足Popov不等式，則該轉速估算系統(tǒng)的穩(wěn)定性只由線性前向通道的傳遞函數G(s)的嚴格正實性決定。首先求出前向通道傳遞函數矩陣G(s)的表達式，將式(5)在S域展開為

(8)

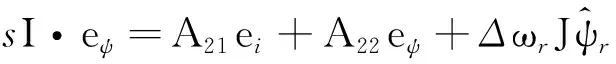
展開可得

(10)

化簡，得

(11)

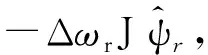
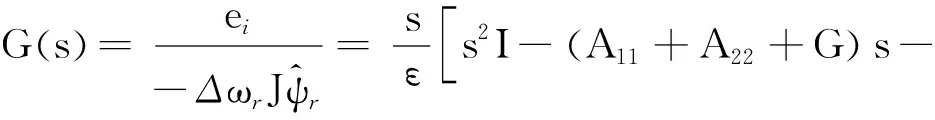
(12)

其中：

y=-g2-ωr

如果前向通道傳遞函數矩陣G(s)嚴格正實，則必須滿足式(13)。

G(jω)+G*(jω)>0 ?ω>0

(13)

其中，G*(jω)是G(jω)的共扼轉置矩陣，將式(12)帶入上式中可得

(14)

其中：

B(s)= ss*(s+s*)I+2ss*xI+ (s+s*)mI+(s*-s)nJ

(15)

可得當且僅當以下條件成立時，式(13)才成立。

B(s)>0

(16)

將s=jωe代入式(16)，ωe為同步角頻率，式(16)展開，可得

(17)

由式(17)可得保證前向通道傳遞函數矩陣嚴格正實的條件為

(18)

式(18)化簡可得

(19)

將式(19)中的ωc稱為臨界頻率，具體定義為

(20)

式(19)即為保證基于偽降階磁鏈觀測器轉速估算系統(tǒng)的線性前向通道傳遞函數G(s)嚴格正實的約束條件，也即保證轉速估算系統(tǒng)滿足Popov超穩(wěn)定性定理的約束條件。

由穩(wěn)定約束條件式(19)和式(20)可知，臨界頻率與偽降階磁鏈觀測器的反饋增益矩陣相關，臨界頻率越小，則不穩(wěn)定區(qū)域也會越小；若將臨界頻率設計為0，則可將不穩(wěn)定區(qū)域收縮到最小，所以反饋矩陣的設計準則是

(22)

簡化得

(23)

式(23)即為保證系統(tǒng)穩(wěn)定的反饋增益矩陣的設計準則。根據該準則，可以將反饋矩陣設計為

(24)

由式(24)可知，反饋增益矩陣設計簡單，與電機轉速無關。

3 仿真驗證

為驗證基于偽降階磁鏈觀測器的轉速辨識算法的有效性，在MATLAB環(huán)境下搭建了仿真模型。仿真模型中電機參數與實際電機相同，參數如下：PN=3kW，f=50Hz，IN=6.9A，n=1400r/min，Te=20N·m，Rs=1.85Ω，Rr=2.658Ω，Ls=0.2940 H，Lr=0.2898H，Lm=0.2838H，np=2。

電機正反轉運行時的仿真結果如圖3所示。在0s時給定轉速為750r/min；1.5s時，給定轉速變?yōu)?750r/min。從圖3中可知，觀測轉速很好地跟蹤實際轉速，轉速響應速度快，電流和磁鏈的跟蹤性能很好，穩(wěn)定后保持正弦變化。

低速時，電機帶額定發(fā)電性負載的運行結果如圖4所示。在1s時突加額定發(fā)電性負載，電機轉速波動后又保持在100r/min，轉矩電流分量響應速度快，沒有出現不穩(wěn)定現象，轉速觀測系統(tǒng)保持穩(wěn)定。

圖3 正反轉運行波形

圖4 100r/min時，突加額定發(fā)電性負載運行波形

4 試驗結果

為了進一步驗證本文提出的方法的有效性，通過試驗進行了驗證。主電路采用IGBT模塊構成一個三相電壓源逆變器，開關頻率為4kHz，控制系統(tǒng)以dsPIC30F6010A為控制核心，采用矢量控制策略。為了比較觀測性能，通過一個光電編碼器來檢測電機的實際轉速。

電機轉速給定為額定轉速1400r/min時，實際電機轉速和觀測電機轉速的波形如圖5所示。電機轉速給定為125r/min時，實際電機轉速和觀測電機轉速的波形如圖6所示。從圖6可知，不管是在高速還是在低速，電機的轉速觀測值可以較好地跟蹤電機實際轉速，誤差較小。電機轉速為125r/min時的速度辨識結果如圖7所示。由圖7可知，對應的磁鏈角度變化，保持周期性變化，轉子磁鏈α軸的分量如圖8所示，穩(wěn)定為正弦量，可以看出磁鏈觀測器同樣具有較好的觀測性能。

圖5 給定轉速為1400r/min時，速度辨識結果

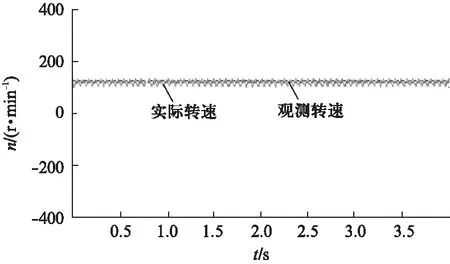
圖6 給定轉速為125r/min時，速度辨識結果

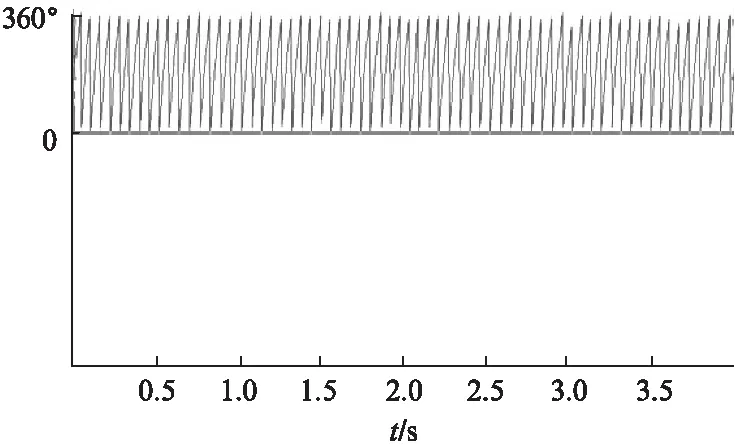
圖7 磁鏈角度變化波形

圖8 轉子磁鏈α軸分量波形

突加突減負載時，電機的觀測轉速和轉矩電流分量的變化波形如圖9所示。電機先空載穩(wěn)定運行于1400r/min，然后突然加額定負載，從圖中可以看出電機轉速先有略微下降，然后調節(jié)到額定轉速，轉矩電流分量增大并能夠保持穩(wěn)定，接著突然減去額定負載，轉速略微上升，然后保持為額定，轉矩電流分量減小到0。

電機給定轉速為300r/min時，突加突減負載的試驗結果，可以看出具有和額定轉速時相當的性能，電機轉速受負載變化的影響較小，轉矩電流分量響應快。不管是在高速還是低速，系統(tǒng)都能保持穩(wěn)定運行。

圖9 給定轉速為1400r/min時，負載變化試驗結果

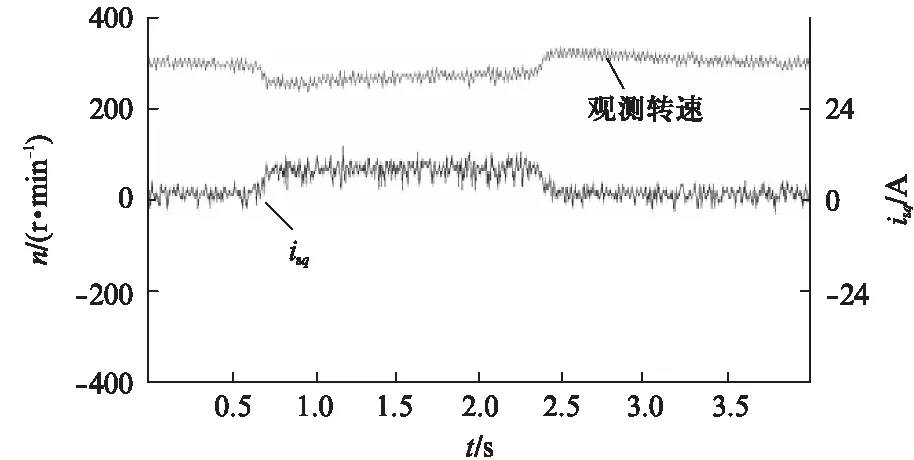
圖10 給定轉速為300r/min時，負載變化試驗結果

5 結 語

本文提出了一種基于偽降階磁鏈觀測器的速度辨識方法，詳細分析了該方法的基本原理，依據Popov超穩(wěn)定理論設計了反饋增益矩陣，獲得了滿足觀測器穩(wěn)定性的條件，保證了電機低速運行的穩(wěn)定。仿真和試驗驗證了該方法的可行性和實用性，從低速到高速范圍，電機都能穩(wěn)定運行，無不穩(wěn)定現象。

【參考文獻】

[1] SUWANKAWIN S, SANGWONGWANICH S . Design strategy of an adaptive full-order observer for speedsensorless inductionmotor drivestracking perfo-rmance and stabilization [J]. IEEE Trans on Industry Electronics, 2006,53(1)： 96-119.

[2] 陳名輝,阮毅,宗劍,等.無速度傳感器在礦用電機車矢量控制系統(tǒng)中的應用[J].電機與控制應用,2012,39(2)： 17-20.

[3] KUBOTA H, MATSUSE K, NAKANO T. DSP based speed adaptive flux observer of induction motor. IEEE Trans Ind Applicat, 1993， 29(2)： 344-348.

[4] YANG G, CHIN T H. Adaptive speed identification scheme for a vector controlled speed sensor-less inverter induction motor drive. IEEE Trans Ind Applicat, 1993， 29(4)： 820-825.

[5] LIN Y N, CHEN C L. Adaptive pseudo-reduced-order flux observer for speed sensorless field oriented control of IM. IEEE Trans Ind Electron, 1999， 46(5)： 1042-1045.

[6] KOJABADI H M, CHEN C L. A MRAS-based adaptive pseudoreduced-order flux observer for senso-rless induction Motor Drives. IEEE Trans on Power Electronics,2005, 20(4): 930-938.