時間序列分析在橡膠白粉病預測中的應用研究

蔣龍燕，羅大全，車海彥，楊 毅，曹學仁*，殷永濤

(1.海南大學環境與植物保護學院，海口 570228； 2.中國熱帶農業科學院環境與植物保護研究所，海口 571101；3.農業部熱帶作物有害生物綜合治理重點實驗室，海口 571101； 4.海南省農業技術推廣服務中心種子站，海口 570203)

時間序列分析在橡膠白粉病預測中的應用研究

蔣龍燕1,2,3，羅大全2,3，車海彥2,3，楊 毅2,3，曹學仁2,3*，殷永濤4

(1.海南大學環境與植物保護學院，海口 570228； 2.中國熱帶農業科學院環境與植物保護研究所，海口 571101；3.農業部熱帶作物有害生物綜合治理重點實驗室，海口 571101； 4.海南省農業技術推廣服務中心種子站，海口 570203)

運用指數平滑法、自回歸分析法、移動平均分析法、自回歸移動平均法對1962-2003年期間海南農墾橡膠樹白粉病的病情指數進行預測，并對這4種方法研究結果進行比較。結果表明，4種分析方法均能較好地預測橡膠白粉病的發生趨勢，但自回歸移動平均法的預測效果較好。因此可以利用時間序列分析法預測橡膠白粉病。

橡膠白粉病； 病情指數； 時間序列分析

天然橡膠是一種重要的戰略物資，與煤炭、石油、鐵礦石并稱為四大工業原料，在國民經濟建設中發揮著不可替代的作用。由橡膠樹粉孢菌(OidiumheveaeSteinm)侵染引起的橡膠樹白粉病是世界橡膠樹上的重要病害之一，主要危害橡膠樹的嫩葉、嫩芽、嫩梢和花序，病重時對橡膠樹的生長和產量均有顯著影響，造成較大的經濟損失[1]。海南是我國橡膠樹的主要種植區之一，1959年橡膠白粉病在海南農墾第一次大流行，以后每年均有發生，甚至在一些年份全面流行，成為海南農墾橡膠樹的主要病害。

時間序列分析是數理統計預測的一種，是采用模型對所觀察到的有序隨機數據進行分析與處理的一種方法，常用的有滑動平均法、指數平均法、季節交乘法、季節疊加法、方法分析周期外推法、馬爾科夫鏈法和自回歸滑動平均法等[2]。該方法已經在人類和動物疾病預測研究中得到了廣泛應用[3-8]。在植物病害預測研究方面，Yang和Zeng用時間序列分析法對我國1950-1990年不同地區小麥條銹病的流行進行了分析，結果發現菌源區和流行區的病情可用不同的模型擬合[9]；華來慶等用ARIMA模型對黃瓜霜霉病疾病指數時間序列進行了研究，建立了自回歸模型，模型擬合效果較理想[10]；任建國等利用AR模型預測柑橘潰瘍病的發生情況，發現所建AR模型可以精確預測潰瘍病發生趨勢[11]；康曉慧等運用三種時間序列分析模型對水稻稻瘟病進行了預測，結果3種方法的預測擬合度均在96%以上[12]。本研究采用時間序列分析中的指數平滑法(exponential smoothing，ES)、自回歸分析法(auto-regressive，AR)、移動平均分析法(moving-average，MA)和自回歸移動平均法(auto-regressive and moving average，ARMA)對1962-2001年海南農墾橡膠樹白粉病的病情指數進行擬合,并對擬合結果進行了比較分析，以期為海南農墾橡膠樹白粉病的流行預測提供參考。

1 材料和方法

1.1 數據來源

1962-2003年海南農墾橡膠樹白粉病的病情指數數據來源于《海南農墾橡膠樹病蟲害防治五十年》一文(表1)[13]。其中以1962-2001年的病情指數數據建模，2002年和2003年的病情指數數據檢驗模型的預測效果。

表11962-2003年海南農墾橡膠白粉病病情指數

Table1DiseaseindexofrubbertreepowderymildewinHainanStateFarmsduring1962-2003

年份Year病情指數Diseaseindex年份Year病情指數Diseaseindex年份Year病情指數Diseaseindex年份Year病情指數Diseaseindex196221．219735．4198448．3199555．0196316．1197427．3198541．3199644．0196429．7197525．1198646．8199732．5196522．6197612．2198752．7199852．8196633．6197738．2198854．0199924．1196719．1197860．2198947．6200047．8196817．8197921．6199049．9200153．1196940．8198046．1199145．1200234．4197024．7198118．8199244．1200324．719717．9198225．5199346．0197229．2198336．8199444．9

1.2 時間序列分析方法

1.2.1 ES法

是對歷史數據的加權平均，它可以用于任何一種沒有明顯函數規律，但確實存在某種前后關聯的時間序列的短期預測。到時期t-1時，只需知道時期t-1的實際數值和本期預測兩個數據值就可預測時期t的數值，其模型如下：

St=αYt-1+(1-α)St-1

式中：St是時間t的預測值，Yt-1是時間t-1的實際值，St-1是時間t-1的預測值，α是平滑常數，其取值范圍為[0,1]。

1.2.2 AR模型法

利用前期若干時刻的隨機變量的線性組合來描述以后某時刻隨機變量的線性回歸模型。主要是根據對時間序列求其本期與不同滯后期的一系列自相關系數和偏自相關系數以識別其特性,主要用偏自相關系數來判定模型的階數，p階自回歸AR(p)模型的表達式如下：

St=a1Yt-1+a2Yt-2+…+at-pYt-p+εt

式中：St是時間t的預測值，a1、a2…at-p是自回歸系數，Yt-1、Yt-2…Yt-p是t-1、t-2…t-p期的觀測值，p是自回歸項數，εt是白噪聲序列(零均值的平穩序列)。

1.2.3 MA模型法

是根據時間序列資料，采取逐項移動平均的辦法，計算一定項數的序時平均數，以反映長期趨勢的方法。主要用自相關系數來判定模型的階數，q階移動平均MA(q)模型的表達式如下：

St=εt-θ1εt-1-θ2εt-2-…-θqεt-q

式中：St是時間t的預測值，εt、εt-1、εt-2…εt-q是白噪聲序列，θ1、θ2…θt-q是移動平均系數，q是移動平均項數。

1.2.4 ARMA模型法

是研究時間序列的重要方法，由AR模型與MA模型為基礎“混合”構成。在進行模型的參數估計之前，首先需要對數據有無隨機性、平穩性和季節性進行判定。其表達式為：

St=a1Yt-1+a2Yt-2+…+at-pYt-p+εt-θ1εt-1-θ2εt-2-…-θt-qεt-q

式中各變量定義同上。

1.3 模型的比較

模型精度主要是通過預測值與實測值的相關系數(r)和均方根誤差RMSE(root mean square error)來驗證。RMSE計算公式為：

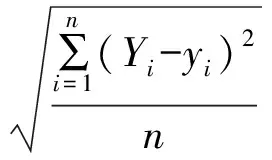
式中：Yi，yi分別為估算值和實測值。

時間序列分析采用Eviews6.0軟件。

2 結果與分析

2.1 數據平穩性檢驗

在對數據進行平穩性檢驗之前，利用Eviews軟件對橡膠白粉病病情指數數據是否符合正態分布進行了檢驗，結果W=0.959，P=0.132>0.05，表明符合正態分布。利用單位根ADF檢驗法對數據進行平穩性檢驗，計算得到的ADF的檢驗值為-4.294 6，P=0.0015<0.01，表明數據是平穩的，可直接用于時間序列分析。

2.2 時間序列模型預測值和實際值的比較

利用Eviews軟件分別對1962-2001年海南農墾橡膠白粉病病情指數數據的ES模型、AR模型、MA模型和ARMA模型的參數進行了估計，建立了預測模型，結果各模型的r2分別為0.3203、0.278 5、0.508 1和0.5461，均達到了極顯著水平。從其預測值和實際值的曲線擬合圖(圖1)可以看出，利用4種模型得到的橡膠樹白粉病病情指數均可反映橡膠白粉病的流行趨勢和變化動態。

圖1 時間序列分析模型對1962-2001年海南農墾橡膠白粉病的預測值與實測值的擬合度比較Fig.1 Comparison between the actual value and estimated value of disease index of rubber tree powdery mildew in Hainan State Farms during 1962-2001by 4 time series analysis methods

2.3 4種時間序列分析法的比較

通過計算預測值與實際值的相關系數(r)和RMSE來評價4種時間序列分析方法在橡膠白粉病病情指數預測中效果的優劣(表2)。從表中可以看出，ARMA模型法預測值和實際值的r值在4種方法中最大，為0.7268，RMSE值最小為9.68，表明利用該模型擬合橡膠白粉病病情指數的效果最好，而AR模型在4種模型中的預測效果最差。

表24種時間序列分析方法對1962-2001年海南農墾橡膠白粉病擬合效果的比較

Table2Comparisonoftheforecastingeffectsofrubbertreepowderymildewby4timeseriesanalysismethods

模型ModelrFvaluePRMSEES模型ESModel0．565919．06<0．00111．98AR模型ARModel0．507713．510．00112．20MA模型MAModel0．700339．46<0．00110．09ARMA模型ARMAModel0．726842．13<0．0019．68

2.4 4種時間序列分析法在橡膠白粉病病情指數預測中的應用

利用4種時間序列分析方法預測2002年和2003年海南農墾橡膠白粉病病情指數結果見表3。其中2002年4種方法中，除ES模型法的預測值和實際值的相對誤差較大為30.35%外，AR模型、MA模型和ARMA模型的相對誤差分別為10.77%、7.34%和0.22%，但2003年4種方法預測值和實際值的相對誤差均較大，分別為71.65%、74.83%、43.13%和49.60%。

表34種時間序列分析方法對2002年和2003年海南農墾橡膠白粉病的預測效果

Table3DiseaseindexofrubbertreepowderymildewinHainanStateFarmsin2002and2003forecastedby4timeseriesanalysismethods

年Year實際值ActualvalueES模型ESModelAR模型ARModelMA模型MAModelARMA模型ARMAModel200234．4044．8430．7036．9334．48200324．7042．4043．1835．3536．95

3 結論與討論

本研究運用ES法、AR法、MA法、ARMA法4種時間序列分析法對海南農墾橡膠樹白粉病發病情況進行擬合預測。研究結果顯示，利用4種模型得到的預測值與實際值的擬合效果較好，其中ARMA模型的擬合效果最好。

在對時間序列模型進行選擇時，應充分考慮各模型的適用范圍、優點及模型的準確度。ES法的優點是能夠把新觀察的值考慮進去，不斷地對模型進行修正；AR模型適用于一些由等時間間隔組成的時間序列數據的預測建模上；MA模型適用于不帶季節變動的反復預測，能有效地消除預測中的隨機波動；ARMA模型適用于各種復雜的時間序列模式[14]，將擬合誤差作為重要因素納入模型中，故該模型預測精度較高。賽曉勇等利用時間序列預測方法在退田還湖區血吸蟲病發病的擬合效果評價研究中發現[4]，ARIMA模型的效果優于ES模型、AR模型和MA模型，本研究也得到了相似的結論。

已有的橡膠白粉病的預測方法主要根據橡膠樹的物候、氣象條件、越冬菌量等因子建立數學模型[15-17]，雖然準確率較高，但需要收集的數據量較多、需要多次田間調查、工作量較大。時間序列分析對資料的要求比較單一，只需變量本身的歷史數據就可實現對變量的預測，因此可以用于預測橡膠樹白粉病的病情指數，大體掌握病害的流行趨勢。雖然利用時間序列分析可以反映海南農墾橡膠白粉病病情指數的變化，但是當病害年度間存在較大差異時(圖1)，利用時間序列得到的結果和實際病情指數相差較大。另外，從本研究中可以看出，利用時間序列分析法適合用歷年的數據對次年的發病趨勢進行預測，若對其他年份進行預測則會誤差較大，這和康曉慧等在稻瘟病上的研究結論一致[12]。由于時間序列分析方法只是利用歷史數據進行預測，并未考慮環境等因素對病害發生的影響，因此在實際應用中，除了不斷加入新記錄數據對模型進行修正，還要考慮當年的環境等因素，并綜合其他的多因子模型預測結果，這樣才能提高對病害的預測準確度。

[1] 劉靜.橡膠樹白粉病的研究進展[J].熱帶農業科技,2010,33(3): 1-5.

[2] 張孝羲,張躍進.農作物有害生物預測學[M].北京:中國農業出版社,2006.

[3] Allard R.Use of time-series analysis in infectious disease surveillance[J].Bulletin of the World Health Organization,1998,76(4): 327-333.

[4] 賽曉勇,邢秦菊,孟定茹,等.五種預測方法在退田還湖區血吸蟲病發病的擬合效果評價[J].第四軍醫大學學報,2006,27(17): 1603-1605.

[5] 鄧丹,王潤華,周燕榮.乳腺癌患者住院醫療費用的時間序列分析應用研究[J].重慶醫科大學學報,2007,32(10): 1065-1069.

[6] 許丹寧,肖建華,王洪斌.3種模型預測豬瘟發病率的比較[J].中國獸醫雜志,2009,45(6): 3-5.

[7] 彭志行,陶紅,賈成梅,等.時間序列分析在麻疹疫情預測預警中的應用研究[J].中國衛生統計,2010,27(5): 549-463.

[8] 欒培賢,肖建華,陳欣.基于灰色模型和ARMA模型的豬瘟月新發生次數預測比較[J].農業工程學報,2011,27(12): 223-226.

[9] Yang X B,Zeng S M.Detecting patterns of wheat stripe rust pandemics in time and space[J].Phytopathology,1992,82(5): 571-576.

[10]華來慶,熊林平,申廣榮,等.自回歸模型在黃瓜霜霉病預測中的應用[J].第二軍醫大學學報,2006,27(7): 729-732.

[11]任建國,黃思良,李楊瑞,等.AR模型在柑桔潰瘍病測報中的應用[J].植物病理學報,2006,36(5): 460-465.

[12]康曉慧,陳浩,張梅.3種時間序列分析模型在水稻稻瘟病預測中的應用[J].西北農林科技大學學報(自然科學版),2011,39(6): 173-177.

[13]海南農墾科技編委會.海南農墾橡膠樹病蟲害防治五十年[J].海南農墾科技,2005,17(2): 34-45.

[14]Peter G,Karl S.Independent sampling of a stochastic process[J].Stochastic Processes and Their Applications,1998,74(2): 151-164.

[15]華南熱帶作物科學研究院植物保護研究所.橡膠樹白粉病預測預報研究[J].熱帶作物學報,1985,6(2): 51-56.

[16]余卓桐,王紹春,周春香,等.橡膠樹白粉病預測模式的研究[J].熱帶作物學報,1985,6(2): 57-66.

[17]余卓桐,肖倩莼,黃武仁,等.橡膠樹白粉病防治決策模型研究[J].熱帶作物學報,2002,23(3): 27-31.

Applicationoftimeseriesanalysisintheforecastingofrubbertreepowderymildew

Jiang Longyan1,2,3, Luo Daquan2,3, Che Haiyan2,3, Yang Yi2,3,Cao Xueren2,3, Yin Yongtao4

(1.CollegeofEnvironmentandPlantProtection,HainanUniversity,Haikou570228，China; 2.EnvironmentandPlantProtectionResearchInstitute,CATAS,Haikou571101，China; 3.KeyLaboratoryofIntegratedPestManagementonTropicalCrops,MinistryofAgriculture,Haikou571101，China; 4.HainanProvinceAgriculturalTechnologyExtensionandServiceCenterSeedStation,Haikou570203,China)

Disease index of rubber tree powdery mildew in Hainan State Farms during 1962-2003was predicted using 4 time series analysis methods including exponential smoothing (ES),autoregressive (AR),moving average (MA) and autoregressive and moving average (ARMA).The forecasting effects of these four methods were compared.The results showed that the occurrence trend of rubber tree powdery mildew can be preferably fitted by the 4 methods,and ARMA had the fittest predicting effect.Therefore,time series analysis can be used for rubber tree powdery mildew forecasting.

rubber tree powdery mildew; disease index; time series analysis

2013-07-01

：2013-07-12

中央級科研院所基本科研業務費專項(No.2013hzs1J004)；海南大學“211工程”建設項目

S 435.76

：ADOI：10.3969/j.issn.0529-1542.2014.02.015

致謝：感謝海南省農墾總局的吳嘉漣老師對本研究提供的幫助。

* 通信作者 E-mail： caoxueren1984@163.com