病態線性模型參數估計的主元加權迭代法
王永弟,趙好好
(南京信息工程大學 遙感學院,江蘇 南京 210044)
一、引 言
病態性問題存在于測量數據處理、地球物理參數反演、回歸分析等與參數估計有關的諸多領域,其危害嚴重性受到相關領域科技工作者的廣泛關注。當模型中存在病態性時,參數最小二乘估計的性質會顯著地變壞,參數估值的質量難以得到保證。分析模型的病態性質、克服或減弱模型病態性、取得更為準確的參數估值,是當前測量平差中的一個重要問題。
近年來,關于如何解決滿秩、秩虧和附有條件的參數平差模型中的病態問題,得到了測繪地理信息界普遍的重視,許多學者[1-8]對此進行了深入而系統的研究,并取得了一系列重要的成果。在諸多克服或減弱模型病態性的方法中,一大類是以嶺估計、廣義嶺估計、主成分估計和Stein壓縮估計等為代表的有偏估計,其實質是以犧牲最小二乘估計的無偏性來換取參數估計的穩定性和參數估值的可靠性,具有結果有偏和參數確定困難兩個缺點;另一大類是以矩陣的奇異值分解法、遺傳算法及誤差方程的正交化等為代表,其原理都比較深奧,在實際工作中應用不便。
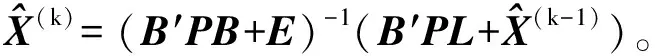
文獻[9]中提出一種新的迭代算法——主元加權迭代法,其主要思想是采用主元加權的預處理手段。即首先降低系數矩陣的條件數,隨著條件數的降低,其病態性也會隨之得以改善和消除;然后組成一個簡單的迭代公式進行求解,經過這樣的處理以后,數值解的精度能夠得到較大幅度的提高。
本文將文獻[9]提出的主元加權迭代法引入到測量數據處理中,以觀察主元加權迭代是否能夠達到與譜修正迭代法相同的效果。分別就良態和病態兩種情況選擇了兩個實際算例,主要對主元加權迭代法和譜修正迭代法兩種方法在不同情形下的表現進行了對比和分析。
二、主元加權迭代方法
1. 主元加權迭代法
測量數據處理中存在諸多病態線性方程組,一般為如下形式
Ax=b
(1)
對于病態線性方程組,A和(或)b如果存在一個小的擾動δA和(或)δb,則會對解產生比較大的誤差。誤差放大的倍數用系數矩陣的條件數cond(A)來衡量,當系數矩陣嚴重病態時,cond(A)?1。
若采用主元加權方法,改善病態矩陣條件數,形式如下
A+αE
(2)
式中,A為n階正定方陣,E為n階單位矩陣。
關于矩陣A+αE的條件數改善問題,文獻[9]給出定義及其證明,在此僅給出定義,證明詳見文獻[9]。
定義:對于正定對稱矩陣A,當α>0 時,則cond(A+αE) 權因子α的選取是否得當是主元加權方法是否有效的關鍵。當α值過小時,對矩陣A的條件數改善效果不明顯,則A仍嚴重病態,此時解的精度仍然很低;當α值過大時,收斂速度則會變慢,甚至解會失真。文獻[9]根據文中所處理的系數矩陣,在Matlab中經過多次計算后確定α取值為2時比較合適。 測量數據處理中存在諸多病態線性方程組,一般為如下形式 Ax=b (3) 將式(3)的主元疊加一個權值來改善條件數,則得到與式(3)同解的另一種形式 (A+αE)x=b+αx (4) 由于式(4)兩端分別含有解向量x,則可構造迭代公式為 (A+αE)x(k+1)=b+αx(k) (5) 令x(k+1)=x(k)+e(k),則 (A+αE)(x(k)+e(k))=b+αx(k)?(A+αE)x(k)+(A+αE)e(k)=b+αx(k)?(A+αE)e(k)=b-Ax(k) (6) 針對平差問題中的良態和病態兩種情況,下面利用高斯約化法、譜修正迭代法和主元加權迭代法等3種方法,通過實例對良態和病態兩種實際平差問題分別進行討論。 本例取自文獻[11]第130頁中的例7~9。在該三角網坐標平差中,得到的法方程為 (7) 法方程系數矩陣的條件數為2.714 7,因此該法方程為良態方程。利用高斯約化法、譜修正迭代法和主元加權迭代法3種方法分別進行計算,計算結果見表1。 表1 計算結果 表1中,所有結果在3種方法中完全相同。由以上結果可知,當平差問題中的法方程為良態時,無論是譜修正迭代法還是主元加權迭代法,均能得到與高斯約化法完全一致的計算結果。 本例取自文獻[3]。其中的法方程為 (8) 表2中,3種方法的參數估值與模擬真值之差的2-范數分別為:31.826 2(高斯約化法)、0.341 5(譜修正迭代法)和0.000 9(主元加權迭代法)。由以上計算結果可知,當法方程為病態方程時,譜修正迭代法和主元加權迭代法均顯著優于高斯約化法,即這兩種方法都能很好地改善最小二乘估計,其中主元加權迭代法的改善效果更為明顯。 表2 計算結果 在良態法方程平差問題中,使用主元加權迭代法能得到與譜修正迭代法和高斯約化法完全一致的計算結果;在病態法方程平差問題中,主元加權迭代法得到的結果比譜修正迭代法和高斯約化法的結果更加明顯地接近真值。因此,從實際應用的角度來講,主元加權迭代法是一種非常實用的計算方法。因此,當在使用主元加權迭代法來解決一般的平差問題時,無論方程有無病態,均可使用完全相同的測量數據處理程序平差,大大增強了數據處理程序的適用性。但實際工作中參數的真值往往無法獲得,計算結果的好壞均是通過參數估值與模擬真值之差的2-范數來比較估值精度的改善程度,因此,是否有更加合理的針對結果改善程度的評估方法,還有待進一步研究。 參考文獻: [1] 盧秀山.病態系統分析理論及其在測量中的應用[D].北京:中國科學院,1999. [2] 王新洲.非線性模型參數估計理論與應用[M].武漢:武漢大學出版社,2002. [3] 王新洲,劉丁酉,張前勇,等.譜修正迭代法及其在測量數據處理中的應用[J].黑龍江工程學院學報,2001,15(2):1-6. [4] 王振杰.大地測量中不適定問題的研究[D].北京:中國測繪科學研究院,2003. [5] 吳杰,李明峰,余騰.測量數據處理中病態矩陣和正則化方法[J].大地測量與地球動力學,2010,30(4):102-105,108. [6] 吳杰,苗恒嚴.測量數據處理中病態矩陣和部分有偏估計方法[J].測繪通報,2010(9):9-11. [7] HOERL A E,KENNARD R W. Ridge Regression: Biased Estimation for Nonorthogonal Problems [J]. Technom etrics,1970,12(1):55-67. [8] 葛旭明,伍吉倉.病態總體最小二乘問題的廣義正則化[J].測繪學報,2012,41(3):372-377. [9] 唐麗,李鵬飛.主元加權迭代法求解病態線性方程組[J].科學技術與工程,2012,12(2):381-383. [10] 武漢測繪科技大學測量平差教研室.測量平差基礎[M].3版.北京:測繪出版社,1996.2. 主元加權迭代算法計算步驟
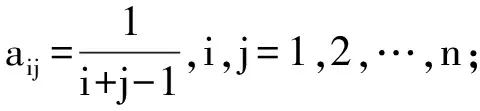
三、實例應用
1. 法方程良態的平差問題
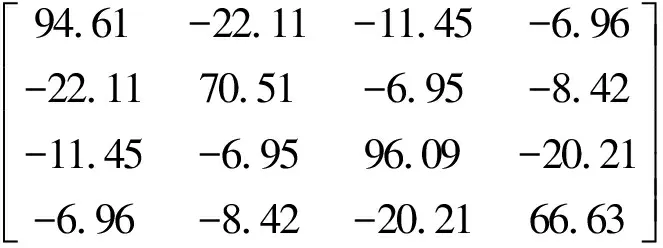
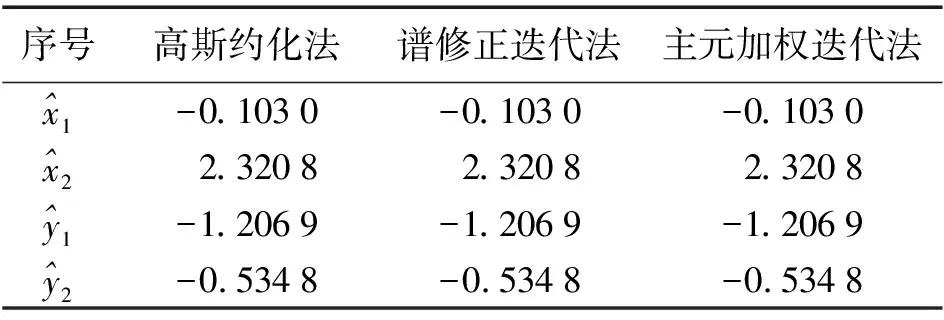
2. 法方程病態的平差問題
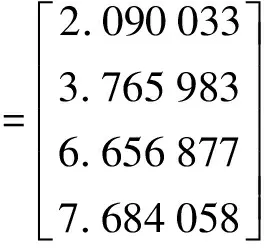
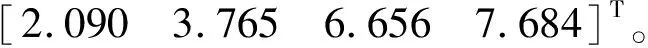

四、結束語

