識別函數圖象的幾種方法

闞元元（遼寧省沈陽市光明中學）

在中考的選擇題中，有一類函數圖象的識別問題.這類問題主要考察學生對函數圖象的分析和理解，求解時主要應用函數解析式、函數的增減性、自變量的取值范圍等知識，結合排除法，對函數圖象進行判斷和識別，其中蘊含著數形結合的數學思想.

一、根據函數的增減性識別函數圖象

例1（2012年重慶市中考題）2012年“國際攀巖比賽”在重慶舉行.小麗從家出發開車前去觀看，途中發現忘了帶門票，于是打電話讓媽媽馬上從家里送來，同時小麗也往回開，遇到媽媽后聊了一會兒，接著繼續開車前往比賽現場.設小麗從家出發后所用時間為t，小麗與比賽現場的距離為S.下面能反映S與t的函數關系的大致圖象是（ ）.

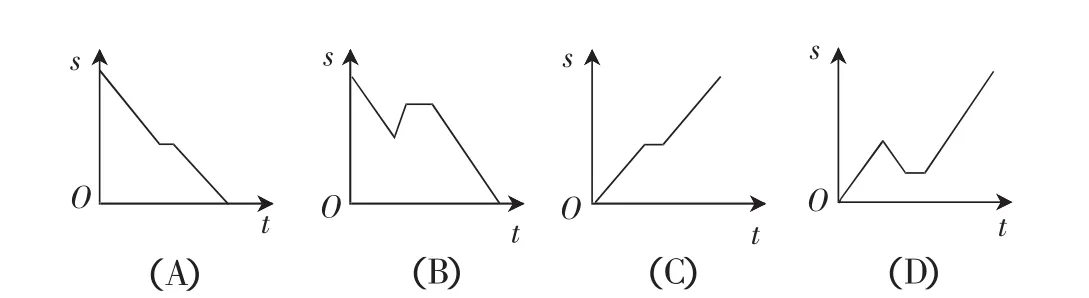
解析：根據題意可得，S與t的函數關系的大致圖象分為四段.

第一段，小麗從出發到往回開，與比賽現場的距離在減小，函數圖象下降；

第二段，往回開到遇到媽媽，與比賽現場的距離在增大，圖象上升；

第三段，與媽媽聊了一會，與比賽現場的距離不變，圖象

第四段，接著開往比賽現場，與比賽現場的距離逐漸變小直至為0，圖象下降.

縱觀各選項，只有B選項的圖象符合.故選B.

點評：在問題情境中，如果函數隨著自變量的增大而增大，則函數圖象是上升的；反之，圖象是下降的.如果自變量變化時函數值保持不變，那么圖象應是水平的.這種根據函數的增減性識別函數圖象的方法比較簡潔，在近幾年各地中考題中有著廣泛的應用.

二、根據函數的類型識別函數圖象

例2（2012年南充市中考題） 矩形的長為x，寬為y，面積為9.則y與x之間的函數關系用圖象表示大致為（ ）.

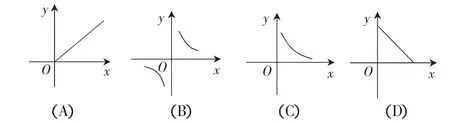
解析：當面積一定時，長與寬是反比例關系，又因為是正數，所以函數圖象是雙曲線在第一象限的部分.選C.

點評：一次函數的圖象是直線，反比例函數的圖象是雙曲線，二次函數的圖象是拋物線.解題時，只需確定兩個變量之間是哪一類函數，就可以快速識別函數圖象.

三、根據變量的特殊值識別函數圖象

例3（2012年廣安市中考題）時鐘在正常運行時，時針和分針的夾角會隨著時間的變換而變化，設時針與分針的夾角為y度，運行時間為t分，當時間從3：00開始到3：30止，圖中能大致表示y與t之間的函數關系的圖象是（ ）.

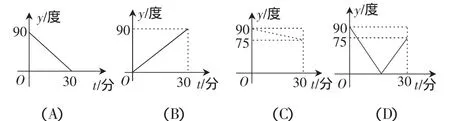
解析：從3：00開始到3：30的過程中，，時針與分針的夾角為90°；t=30，時針與分針的夾角為75°；在運行時間15分到20分的某一時刻時針與分針重合，此時y=0，表示函數圖象與軸的相交.只有D符合.

點評：根據變量的特殊值，確定函數圖象上特殊點（端點、交點）的位置，應用排除法是識別圖象的常用方法.

四、根據函數解析式識別函數圖象

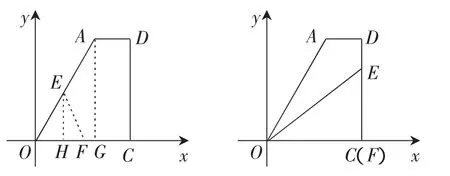
例4（2012年南充市中考題）如圖，直角梯形AOCD的邊OC在x軸上，O為坐標原點，CD垂直于x軸，D（5，4），AD=2.若動點E、F同時從點O出發，E點沿折線OA→AD→DC運動，到達C點時停止；F點沿OC運動，到達C點是停止，它們運動的速度都是每秒1個單位長度.設E運動x秒時，△EOF的面積為y（平方單位），則y關于x的函數圖象大致為（ ）.

解析：根據點D的坐標求得點A的坐標，從而求得線段OA和線段OC的長，然后根據運動時間即可判斷三角形EOF的面積的變化情況.

因為 D（5，4），AD=2，所以 OC=5，CD=4，OA=5.

（1） 當點E在OA運動時，運動x秒（0＜x＜5），此時OE=OF=x，作EH⊥OC于H，AG⊥OC于點G，如下圖.

所以EH∥AG.△EHO∽△AGO.

（2） O點E在AD上運動時（5＜x＜7），點F運動到點C時停止運動，△EOF的面積不變，圖象是水平線段.

（3） 當點E在DC上運動時（7＜x＜11），如下圖，EF=11-x，OC=5，

點評：在一些較復雜的問題中，如果以上的簡潔方法不能識別函數圖象，那么要先求出變量之間的函數解析式，再判斷圖象.

五、根據解析式中的系數符號識別函數圖象

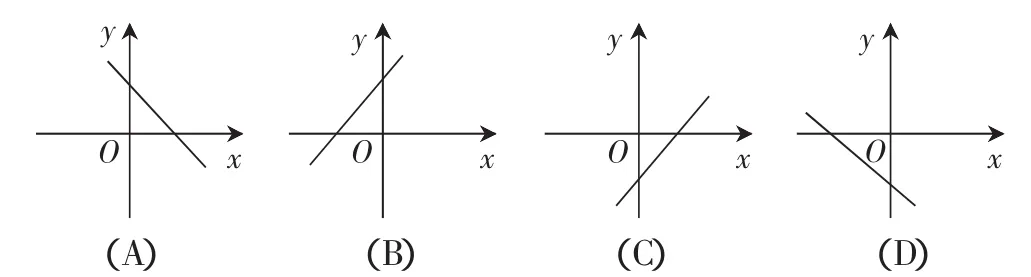
例5（2012年樂山市中考題） 若實數a、b、c滿足a+b+c=0，且a

解析：因為a+b+c=0，

所以a、b、c三個數中至少有一個正數和負數.

因為a

所以函數y=ax+c的圖象是下降的，并且與軸的交點在軸的上方.

應選A.

點評：根據函數的性質，只要能確定解析式中系數的符號，就可以判斷圖象在坐標系中的位置，從而識別出正確的圖象.