重視數學閱讀能力的培養

沈琴 李媛（江蘇省宜興市和橋高級中學）

在高三數學第二輪復習中，我們在批改學生試卷時，發現學生低級錯誤不斷，有些是看錯題目，有些是看漏了某些關鍵條件，還有些運用性理由，學生無法得出其實際數學背景；課后與同科組教師談及此事，大家均有同感.仔細淺析其中原因：我們平時授課一般已對所需講授內容進行加工提煉，評講試題也是對易錯易漏之處重點強調，這樣就造成了學生被動接受和理解，對基本定義及概念理解不深，其本質是學生數學閱讀能力極度匱乏.

閱讀是人類社會生活的一項重要活動，是人類汲取知識的主要手段和認識世界的重要途徑.一談及閱讀，人們聯想的往往是語文閱讀，而數學是和數字打交道的一門科學，根本無需這種閱讀能力，其實不然，數學中的定理、概念的表述都相當嚴密，如果不具備一定的閱讀能力、理解能力，是很難理解其中所包含的深刻內涵的.前蘇聯著名心理學家龍菲爾德說過：“數學不過是語言所能表達的最高境界，數學也需要閱讀.”語言的學習離不開閱讀，所以數學的學習也不能離開閱讀.從近幾年高考試題的分析來看，高考數學命題已從知識立意逐步轉向能力立意.而數學閱讀能力又是其他數學能力的基礎，縱觀高考應用題的得失分情況及學生的考后反映，最大的問題就是看不懂題意，也就是應用題閱讀能力不強，從而影響了答題效果.許多學生平時只知道做數學題、解數學題，如果讓其講解，把自己的思想展現給其他同學，就十分困難，要么不知道如何表述，要么表述不清，在數學文字語言、符號語言和圖形語言之間的轉換十分欠缺，尤其是把某一實際問題轉換為數學問題來解決，學生就不知所措，不知道如何下手.有時甚至看不懂題目，不知道這一問題與哪一數學知識有關，怎樣轉換為數學問題.構成這些學生學習數學感到困難的因素之一是他們的閱讀能力差，在閱讀和理解數學方面特別無助.因此，要想使數學素質教育目標得到落實，使數學不再讓學生感到難學，就必須重視數學閱讀能力的培養.那么如何提高學生的數學閱讀能力呢？

（一）提供數學學科前沿問題方面的科學著作和科普讀物，激發學生對數學閱讀的興趣，讓學生愿意閱讀數學材料.

興趣是最好的老師，愛好是成功之母.只有激發了學生的興趣和愛好，才能調動學生樂學樂問的心，使其自然而愉快地接受知識.一部好的課外讀物往往可以提高學生的閱讀興趣、引發學生的求知欲、調動學生的學習積極性.歷史上許多數學家都曾在青少年時代受到一些優秀數學書籍的重要影響，不僅從中得到數學的精神、思想和方法的熏陶，而且在他們的一生中留下了難忘的印象.向學生提供好的課外讀物，并幫助和鼓勵他們積極地閱讀，可以使他們開闊知識視野，提高他們獨立獲取知識的能力.每一個知識塊都有“數學與文化”的材料，這也是學生需要重視并閱讀的內容，從中可學到很多.

如在學習數列概念時，選用了這樣的材料:一個真實的故事一列數：3，6，12，24，48，96，192……

普魯士天文學家提丟斯（Titius）推出從太陽到行星距離的經驗定理，并探明了一些新的行星!

觀察上面這列數：

（1）每個數恰好是前一個數字的2倍；

（2）將0加在這列數字的最前面，再將每個數字加4除以10，得到另一列數：0.4，0.7，1.0，1.6，2.8，5.2，10.0，19.6，……

這可不是一列簡單的數字：以地球到太陽的距離為1.0天文單位，則第一個數字表示了太陽到其最近的行星——水星的近似距離，第二個數字表示太陽到金星的近似距離，以此類推，他得到了一張出色的表：

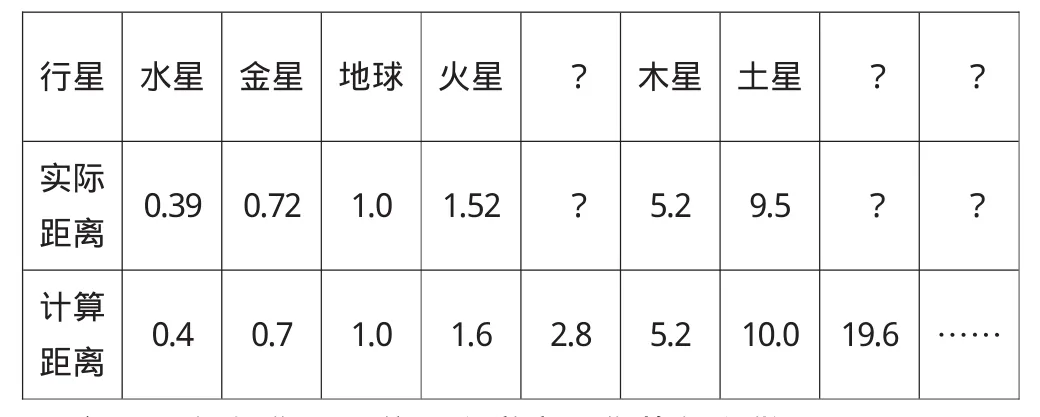
太陽到行星的距離

問題：假如你是一位天文學家，你將怎么做？

在學生充分探討以上問題的基礎上，揭示如下事實：天文學家提丟斯就是利用這張表格預言了天王星的存在，請同學們猜想2.8個天文單位出是否有行星的存在？通過這個活動，激發學生的興趣，然后告知學生，學完本節課后，同學們可以利用本節課的知識繼續研究表格，也許同學們也能預言新的行星的存在，成為天文學家.這里主要的目的是激發學生的興趣和求知欲，同時感悟到學習數學的價值.

（二）重視數學教科書的閱讀，培養良好的閱讀習慣，使學生會讀數學材料.

當學生具有閱讀數學材料的動機和興趣時，教師應教會他們怎么去讀，授之以漁.而數學教科書是數學課程的具體化，不僅是教師教學的主要依據，而且是學生進行學習獲得系統知識的主要材料，它體現了數學的科學性和思想性，在加強數學基礎知識和基本技能的同時結合現實生產、生活及社會實際，并適當滲透當代先進的科學思想，既反映了作為科學的數學的特點，又考慮到學生的學習心理順序，是培養學生數學閱讀能力的最佳材料.而學生不會把閱讀數學教科書作為一種娛樂性閱讀，數學閱讀往往需要付出艱苦的努力.教師指導學生閱讀教科書要循序漸進，從扶讀到引讀最終到放讀，要讓學生了解基本的閱讀方法，使學生能對所學的知識信息進行轉化、解釋及推斷.數學閱讀的核心在于理解，這里面包括了通過聯想建立新舊知識的聯系、對知識系統化形成自己的知識結構以及善于捕捉數學問題.具體閱讀方法如下：

（1）在閱讀的過程中設置適當的問題，引導學生在閱讀過程中積極開展自我啟發思維，對教材提供的“原材料”主動進行“加工”，而自我構建起實質意義上的、非人為給予的數學知識“產品”.古語有云：“學貴有疑，小疑則小進，大疑則大進，疑者覺悟之機也，一番覺悟一番長進.”因此，要特別注意培養學生在數學閱讀中的問題意識.如：在閱讀“誘導公式”一節時，除了要抓主概念中的關鍵字外，要理解五個問題：

1） 利用哪個公式，可以把任意角轉化為0°-360°間的角？

2） 利用哪個公式，可以把 90°-360°轉化為 0°-90°間的角？

3） sin（180°+ α）=-sinα，cos（180°+ α）=-cosα，tan（180°+α）=tanα這組公式推導過程是怎樣進行的？其中α的取值范圍有限制嗎？

4） 教材中的誘導公式（一）和（二） 有何應用？

5） 求 sin750°，cos（2+7π），tan960°的值

（2）提煉數學思想方法，增強數學理解力.數學思想是數學活動的基本觀點.數學方法是在數學思想的指導下，為數學活動提供思路和邏輯手段以及具體操作原則的方法.數學思想方法則是數學知識發生過程的提煉、抽象、概括和升華，是對數學規律的更一般的認識，它蘊含在數學知識之中，需要學習者去挖掘.

在高三復習解析幾何時碰到這樣一題：點P（1，1）是圓O：x2+y2=1，O為坐標原點，過P作兩條相異直線與圓O相交于A、B兩點，且直線PA與直線PB的傾斜角互補，試判斷直線OP和AB是否平行？請說明理由.

結論：直線OP與直線AB平行

證法1（解析法）：因為相異直線PA、PB的傾斜角互補，所以設直線PA的斜率不k，則直線PB的斜率為-k.

所以直線 PA：y-1=k（x-1），PB：y-1=-k（x-1）.

證法2：（幾何法） 過點P作PQ⊥x軸交圓O于點Q.

因為相異直線PA、PB的傾斜角互補，所以PQ是∠APB的角平分線，所以∠APQ=∠BPQ.所以Q是弧PQ的中點，連接OQ，則OQ⊥AB.因為P（1，1），

所以∠PQx=45°. 所以 Q （1，-1），∠POQ=90°.

所以OP∥AB.

問題：通過閱讀，比較兩種方法，你有什么體會？

在閱讀比較的基礎上，使學生充分體驗到用幾何法優化數學解題過程的作用，也從中得到啟發，產生了用幾何法的強烈欲望，再進行關于幾何法解題的研究也就水到渠成了.

（三）交流閱讀體會，撰寫閱讀報告，讓學生樂于閱讀數學閱讀材料.

學生的數學學習活動總是在班集體中進行的.班集體的學習氣氛、同學之間的相互影響，會有形或無形地影響其成員的學習.班級成員的數學基礎不同，閱讀能力有異，學習自覺程度也不一樣.不定期組織學生交流閱讀數學材料的感受體會，對大面積提高學生的閱讀能力大有裨益.教師應給予適當的指導，以學生為主體，提供一個讓學生進行交流、討論及應用數學的氛圍，相互學習，集體提高.

在閱讀數學材料并進行交流的基礎上，教師適當指導學生撰寫閱讀報告，使學生讀寫結合，手腦并用，促進思維的開拓，是提高閱讀效率的重要途徑.高中數學新課程標準中也增加了“學習總結報告”，將高中數學學習提到一個新的層次，使學生在充滿合作機會的群體交往中，學會溝通、互助、分享和合作，實現知識、情感、態度和價值觀的完善.

總之，重視數學閱讀，培養閱讀能力，符合現代“終身教育，終身學習”的教育思想.眾所周知，未來社會高度發展，瞬息萬變，這決定了未來人不僅要有扎實寬厚的基礎知識功底，更需要他們有較強的自學功底從事終身學習，以便隨時調整自己來適應社會發展的變化.而閱讀是自學的主要形式，自學能力的核心是閱讀能力，因此，教會學生學習的重頭戲就是教會學生閱讀，培養其閱讀能力，數學學習也是如此.