大姿態角入水時的魚雷半實物仿真方法研究

郝 喆，張秦南，王立文，王 中

(1.中國船舶重工集團公司第705研究所，陜西 西安 710075;2.水下信息與控制重點實驗室，陜西 西安 710075)

0 引言

根據實航試驗結果統計，空投魚雷的入水姿態范圍為:航向角:－180°～180°;滾動角: －180°～180°;俯仰角: －30°～ －85°。

采用立式三軸轉臺進行控制系統仿真時，當俯仰角大于－70°情況下，控制系統半實物仿真中會出現發散，導致仿真試驗失敗，或產生強烈的運動學耦合，與數學仿真結果差異較大，而且轉臺的輸入值與輸出值不吻合，試驗結果不可信。

通過重新定義歐拉角以及合理設置轉臺的角速率限幅值和角加速度限幅值可以解決上述問題。本文對大姿態角入水下的半實物仿真問題進行深入分析，針對立式三軸轉臺提出基于正歐拉角或反歐拉角的半實物仿真方法，試驗結果表明仿真方法有效可行，而采用正歐拉角還是反歐拉角，可以事先通過數學仿真進行確定。

1 問題分析和解決方法

1.1 歐拉角定義

繞定點轉動的剛體相對參考坐標系的角位置，可以用3次獨立轉動的3個轉角來確定。這就是著名的歐拉法。這3個獨立的角度稱為歐拉角。在實際使用中歐拉角的選取不唯一，要視具體情況而定［1］。

當選取發射點地理坐標系作為參考坐標系時，通常按航向角ψ、俯仰角θ、滾動角γ的順序旋轉可以得到雷體坐標系。按這樣順序定義歐拉角時，航向角ψ的定義為雷體ox1在水平面的投影與地面坐標系ox軸的夾角，俯仰角定義為導彈縱軸ox1與水平面的夾角，滾動角γ定義為雷體oy1軸與過ox1軸的鉛垂面的夾角。當魚雷處于垂直狀態時，即俯仰角θ為90°時，ox1軸在水平面的投影為1個點，使航向角無意義;過ox1軸的鉛垂面有無窮多個，使滾動角無意義。為了避免俯仰角為90°時滾動角和航向角無意義，需要重新定義1套歐拉角。

參考坐標系 (如發射點地理坐標系)按航向角、滾動角、俯仰角的順序旋轉也可以得到雷體坐標系。航向角定義為雷體坐標系oz1軸在水平面的投影與參考坐標系oz軸的夾角，滾動角定義為雷體坐標系oz1軸與水平面的夾角，俯仰角定義為垂直于oz1軸的平面和水平面的交線與雷體坐標系ox1軸的夾角。由此可見，上述2種歐拉角的定義不同。按航向角、滾動角、俯仰角的順序旋轉定義的歐拉角計為ψ1(航向角)、γ1(滾動角)、θ1(俯仰角)。

1.2 轉臺限幅特性分析

轉臺用于跟蹤仿真計算機解算出的歐拉角，當仿真中解算出的角速率和角加速度大于設定的轉臺限幅值就會出現失真，即轉臺的輸出歐拉角與解算不一致，其實質是仿真應遵循的相似性原理得不到滿足［4－6］。

為了對轉臺限幅特性進行研究和對控制系統發散進行定量分析，在仿真計算機中人為加入幅值為20°、頻率為1 Hz的正弦信號驅動轉臺的滾動框，控制系統跟蹤轉臺信號，仿真結果如圖1所示。轉臺角加速度限幅為500°/s2時轉臺輸出有延遲和幅值衰減，轉臺角加速度限幅為800°/s2時轉臺輸出無延遲和衰減。角速度限幅情況與上述結果類似。

發散原因定位為轉臺3個框的角加速度限幅值低于相應計算值。

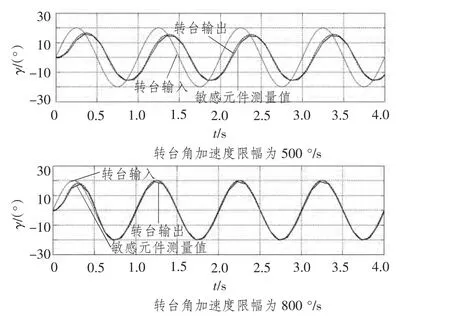
圖1 不同角加速度限幅下轉臺滾動框輸出與敏感元件測量曲線 (轉臺滾動框輸入為幅值為20°、頻率為1 Hz的正弦信號)Fig.1 On the different angle acceleration limiting amplitudc the output of the turn-table roll frame and the measurement curves of sense organ(the input of turn-table roll frame is 20°，frequency is 1 Hz of sine signal)

1.3 正歐拉角方程和分析

歐拉角ψ，θ和γ隨時間的變化規律為:

由式(1)可知，當俯仰角接近－90°時，歐拉角的變化率接近無窮大，而在－90o時方程出現奇異無法求解。由式(1)及其微分可以估算轉臺3個框的角速度和角加速度的最大值。

利用式(1)進行仿真時，解算出的歐拉角ψ，θ和γ分別驅動轉臺的外框、中框、內框，而轉臺每個框的角速率和角加速度一般要進行限幅，解算出的角速率和角加速度大于設定的轉臺限幅值就會出現失真，即轉臺的輸出歐拉角與解算不一致，其實質是仿真應遵循的相似性原理得不到滿足。

1.4 反歐拉角方程和分析

反歐拉角 ψ1，θ1和 γ1隨時間的變化規律為［2］:

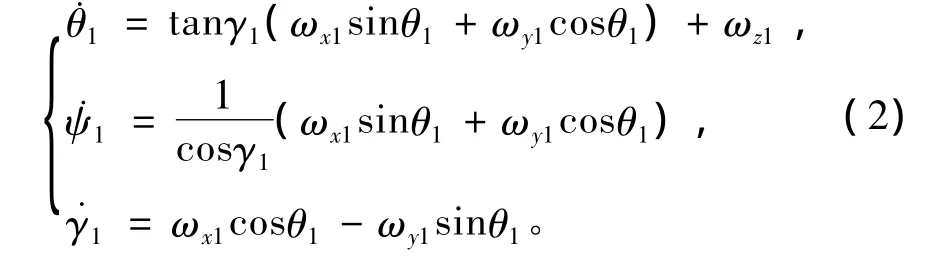
由式(2)及微分可以估算轉臺3個框的角速度和角加速度的最大值。當數學仿真中滾動角γ1小于45o時，則可以進行控制系統半實物仿真，相應歐拉角的角速率可以滿足轉臺每個框的角速率和角加速度的限幅值。當數學仿真時若滾動角γ1接近90°時，也需要重新定義歐拉角。

2 仿真結果

假定正歐拉角ψ，θ和γ的初值為0°，－75°和150°，則反歐拉角 ψ1，γ1和 θ1的初值依次為－150.86°，7.44°和 －103.07°。利用數學仿真進行計算，可以估算試驗中轉臺3個框所需的角速度和角加速度。角速度和角加速度最大計算值 (見表1)。

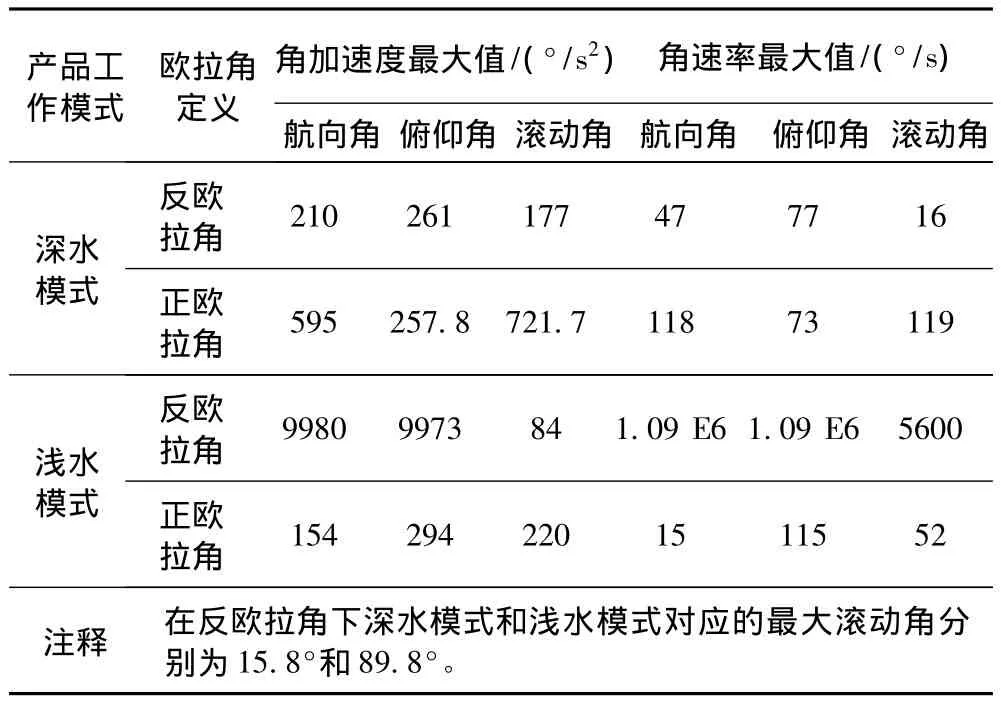
表1 角速度和角加速度最大計算值Tab.1 The max angle rate and angle acceleration

由表1可知，產品工作于深水模式時采用反歐拉角易于進行半實物仿真;產品工作于淺水模式時采用正歐拉角可以進行半實物仿真，而采用反歐拉角時，由于轉臺不能實現相應的最大角速度和角加速度，因而無法進行半實物仿真。

圖2為深水工作模式下控制系統半實物仿真曲線 (采用反歐拉角)。

圖3為淺水工作模式下控制系統半實物仿真曲線 (采用正歐拉角)。

試驗表明，半實物仿真結果與數學仿真結果吻合，說明半實物仿真結果可信，控制系統半實物仿真試驗有效，同時表明仿真方法可行。

3 結語

本文通過合理定義歐拉角及設置轉臺的角速率限幅值和角加速度限幅值可以實現大姿態控制系統的半實物仿真。通過仿真計算和試驗結果分析主要結論如下:

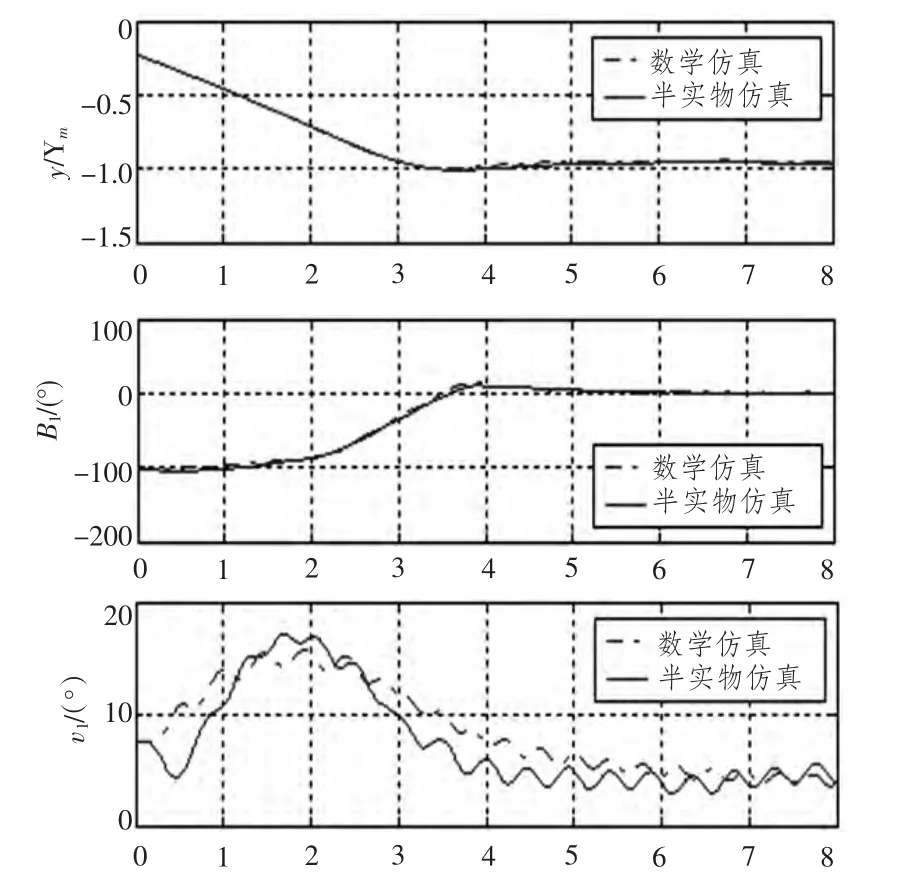
圖2 深水工作模式下控制系統半實物仿真曲線(采用反歐拉角)Fig.2 The semi-physical simulation curves of control system on deep-water work mode(reversed euler method)

圖3 淺水工作模式下控制系統半實物仿真曲線(采用正歐拉角)Fig.3 The semi-physical simulation curves of control system on shallow-water work mode(ordinary euler method)

1)采用立式三軸轉臺進行大姿態控制系統半實物仿真前通過數學仿真可以對轉臺的角速率限幅值和角加速度限幅值進行計算，從而對轉臺的角速率限幅值和角加速度限幅值進行合理的設定;同時確定使用的歐拉角定義;

2)某產品在深水控制模式進行仿真時可以采用反歐拉角驅動轉臺;

3)某產品在淺水控制模式下可以采用常規的正歐拉角進行半實物仿真。

［1］于波，陳云相，郭秀中.慣性技術［M］.北京:北京航空航天大學出版社，1994.YU Bo，CHEN Yun-xiang，GUO Xiu-zhong.Inertial technology［M］.Beijing:Beijing University of Aeronautics and Astronautics Publishing company，1994.

［2］黃雪樵.克服歐拉方程奇異性的雙歐法［J］.飛行力學，1994，12(4):28 －37.HUANG Xue-qiao.Dual-euler method for overcoming singularity of euler equation［J］.Flight Dynamics，1994，12(4):28 －37.

［3］李躍軍，閻超.飛行器姿態解算的全角度雙歐法［J］.北京:北京航空航天大學學報，2007(5):505－508.LI Yue-jun，YAN Chao.Improvement of dual-euler method for full scale eulerian angles solution of aircraft［J］.Journal of Beijing University of Aeronautics and Astronautics，2007(5):505－508.

［4］黃華紅，楊云川，呂艷慧.一種魚雷俯仰角出現±90°時的姿態仿真方法［J］.Torpedo Technology，2012(3):225 －230.HUANG Hua-hong，YANG Yun-chuan，LV Yan-hui.Attitude simulation method for torpedo pitch angle at±90°［J］.Torpedo Technology，2012(3):225 －230.

［5］雷江濤，張秦南，王立文.一種速率陀螺啟動過程的時變增益補償控制技術［J］.艦船電子工程，2012(1):41－42.LEI Jiang-tao，ZHANG Qin-nan，WANG Li-wen.A timevaryin gain compensate control tecnnique for rate gyroscope during its starting period［J］.Ship Electronic Engineering，2012(1):41－42.

［6］王曉晨，趙輝，馬克茂，等.一種新型全姿態飛行仿真轉臺的運動學分析［J］.中國科學:信息科學，2010(4):35 －46.WANG Xiao-chen，ZHAO Hui，MA Ke-mao，et al.Kinematics analyses for a new simulation turn-tables of full attitude flight［J］.Scientia Sinica(Informationis)，2010(4):35－46.