岸式振蕩水柱波能轉換裝置的數值模擬

寧德志，石進，滕斌，趙海濤

(1.大連理工大學海岸和近海工程國家重點實驗室，遼寧大連116024;2.國家海洋局第二海洋研究所工程海洋學重點實驗室，浙江杭州310012)

海洋面積占地球表面積的71%，它不僅為人 類提供航運、水產和豐富的礦藏，而且蘊含著大量的能量。海洋能主要包括波浪能，潮汐能，海洋溫差能，海洋鹽差能和海流能等，其中波浪能作為一種重要的可再生清潔能源具有分布廣泛、能量密度大、采集結構簡單等特點。振蕩水柱式波能轉換裝置(oscillating water column，OWC)是目前各國最為重視、公認的最有前途、投入研究力量最大、建造使用最多的一種裝置。該裝置通過氣室將波浪能轉換為空氣氣流的能量，再通過空氣透平將氣流能量轉換為電機轉軸的軸功，最后通過發電機將轉軸軸功轉換為電能。岸式的振蕩水柱轉換裝置是振蕩水柱波能轉換裝置的一種，它具有結構簡單，易于安裝和維護等特點。關于 OWC的研究有很多。Evans等［1-6］在 OWC的二維和三維頻域勢流理論分析與數值計算中做了很多工作。時域勢流理論方面，Koo等［7-8］采用考慮完全非線性自由水面邊界條件的常數邊界元方法并在氣室內引入壓強模型計算了一種帶底坡的岸式的振蕩水柱波能轉換裝置。Zhang等［9-11］應用基于N-S方程的粘性流模型對振蕩水柱式波能轉換裝置進行了數值模擬。此外，Sarmento等［12-14］實驗研究了振蕩水柱式波能轉換裝置。

本文應用時域高階邊界元方法與壓強模型建立了岸式振蕩水柱波能轉換裝置的二維數值模型，研究了前墻尺寸，氣室寬度及入射波要素對岸式振蕩水柱波能轉換裝置能量轉換效率的影響。

1 OWC時域數值模型

1.1 控制方程和邊界條件

本文研究的岸式振蕩水柱波能轉換裝置如圖1所示，H代表水深，A、B、C、D分別代表氣孔寬度、氣室寬度、前墻壁厚和入水深度。在流體無粘、無旋、不可壓縮的假定下，計算域內流體的速度可用速度勢的梯度表示:

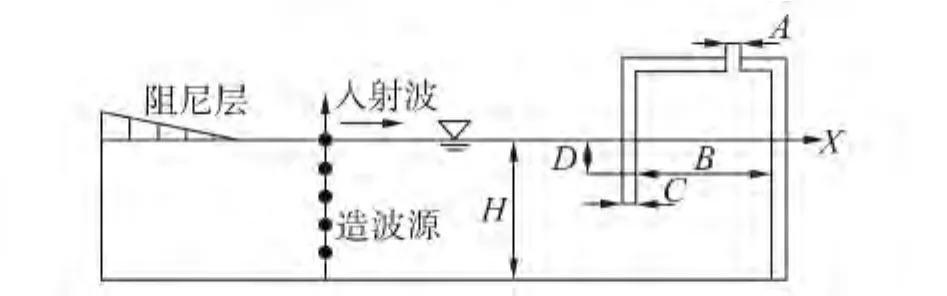
圖1 岸式振蕩水柱波能轉換裝置示意圖Fig.1 Schematic of land-based OWC

本模型采用源造波方法造波，控制方程為泊松方程:

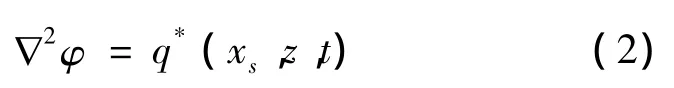
式中:q*(xs，z，t)=2vδ(x-xs)為源造波強度，v為流體質點的水平速度，本文給定為二階Stokes波速度解析解，波浪產生位置x=xs。

在自由水面上，滿足完全非線性運動學和動力學邊界條件:

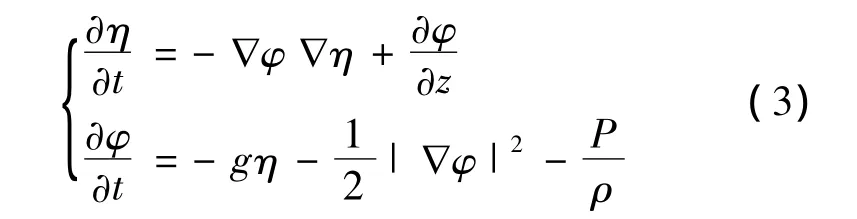
式中:η為自由水面的鉛垂位移，P為自由水面上的壓強，g為重力加速度。本模型采用混合歐拉-拉格朗日法更新自由水面邊界條件，利用物質導數公式d/dt=?/?t+v·?，并在源造波上游區域的自由水面布置人工阻尼層防止波浪反射，自由水面邊界條件轉化成以下形式:

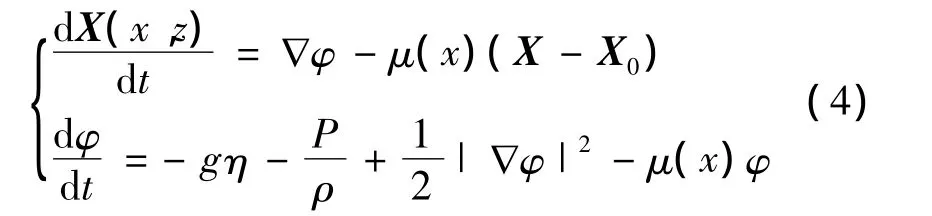
其中:

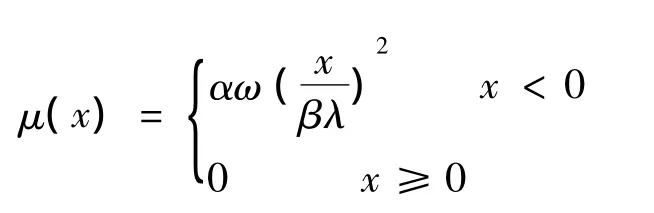
式中:X0=(x0，0)為水質點初始位置，造波位置為x=0，α為阻尼層的阻尼系數，βλ為阻尼層的長度，λ為入射波波長，β為阻尼層寬度系數。

在岸式振蕩水柱波能轉換裝置表面、水槽側壁和水底等固定物體邊界上，流體的法向速度為0，即

本模型在時域內求解，在靜水面上初始條件為

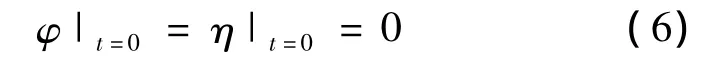
1.2 氣室內的壓強模型

振蕩水柱式波能轉換裝置氣室內的氣體壓強與液面的運動互相影響，存在復雜的氣液耦合現象，需要引入壓強模型加以處理。本模型假定氣室內的壓強與孔口處的氣體流速呈線性關系［7］:

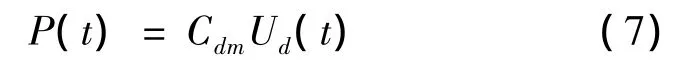
或二次關系［7］:

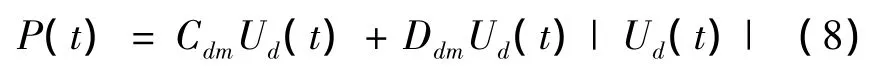
式中:Ud(t)表示氣孔處的氣體流速，Cdm和Ddm分別為線性阻尼系數和二次阻尼系數，它們取決于氣孔處透平的物理特性，例如威爾斯透平兩端的氣體壓強差與流速就基本滿足線性關系，式(8)中的絕對值符號是為了保證壓強符號和孔口處氣體流速方向的關聯性。在孔口氣體流速與氣室內壓強很小的情況下可以假設空氣不可壓縮，由此可得

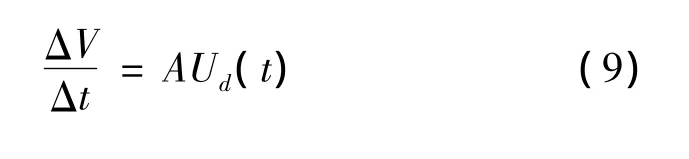
1.3 能量轉換效率的計算

入射波浪會使振蕩水柱波能轉換裝置氣室內的水體做上下振動，從而推動氣室內的氣體在氣孔兩側往復運動，推動透平做功。波浪推動氣體做功的速率可由下式求得

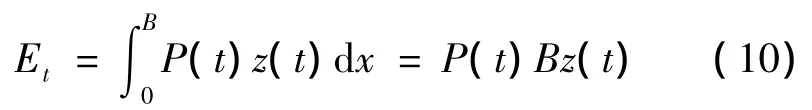
仿照波能流的推導，在一個周期內做平均可得

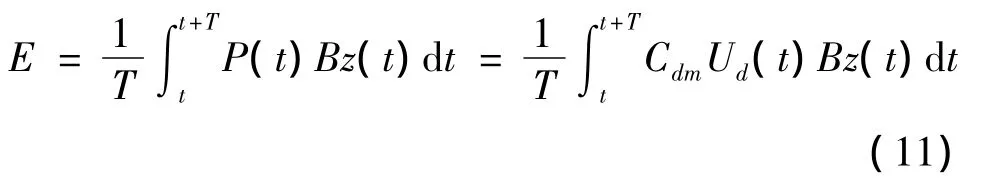
式中:z(t)表示氣室內平均水面的速度。假定氣室內的空氣不可壓縮且孔口處的氣體流速呈正弦變化:

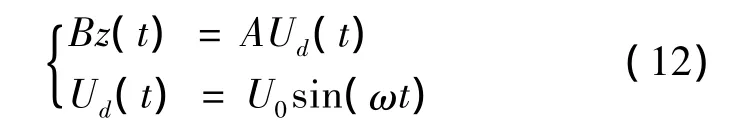
將式(8)、(12)代入式(11)可以推得

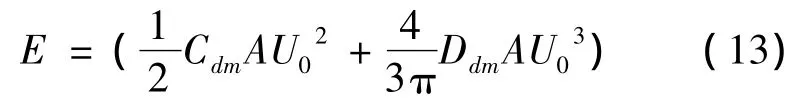
氣室內的能量轉換效率κ可由下式求得

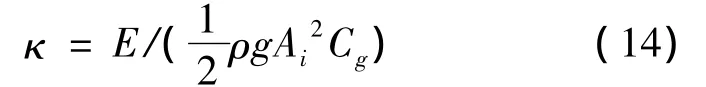
式中:分母為入射波波能流，Ai為入射波波幅，Cg為群速度。

1.4 數值求解

在流體計算域內對速度勢應用第二格林公式，可得到如下邊界積分方程［15］:

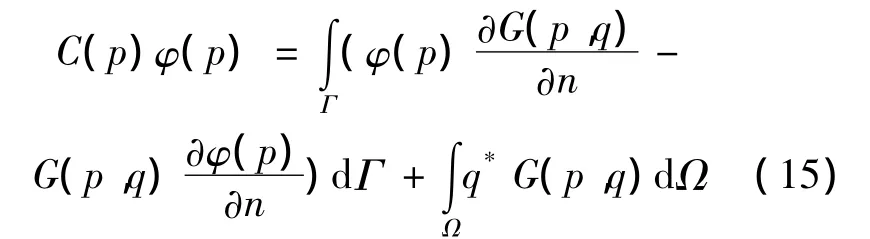
式中:p=(x0，z0)為源點，q=(x，z)為場點，C(p)為固角系數，Γ為包括自由水面邊界和固體邊界的流體計算邊界，Ω代表整個流體計算域。為了消除水底的積分，減小計算量，選取考慮水底鏡像的格林函數:

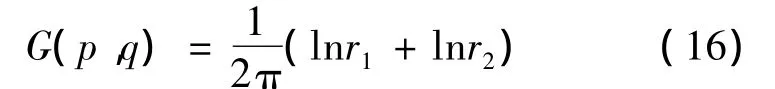
式中:r1為p和q兩點距離，r2為p和q關于水底的鏡像之間距離。

本文用三節點的二次單元將計算域邊界離散成一些曲線單元，每個單元可以通過數學變換變換成參數坐標下的等參元，在等參元內引入形函數可以插值得到單元內任一點的幾何坐標和速度勢。將源點取在各個節點上可以將離散后的積分方程化為線性方程組的形式，從而求解未知量。每一步的計算都認為當前時刻自由水面上的速度勢和物面上的速度勢法向導數是已知的，通過積分方程計算當前時刻自由水面上的速度勢法向導數和物面上的速度勢。在氣室內應用壓強模型后，下一時刻的自由水面上水質點的位置和速度勢可通過四階Runga-Kutta法計算，然后重新劃分網格，繼續應用積分方程計算自由水面上的速度勢法向導數和物面上的速度勢。這樣計算周而復始，直到計算結束［16］。

2 OWC數值模型驗證

氣室內的壓強模型已經成功被用于氣動浮式防波堤的研究中，為了驗證本文壓強模型的準確性，對比計算了文獻［7］研究過的一種氣動防波堤的相應工況。計算水深30 m，氣室寬度30 m，前、后墻壁厚10 m，入水深度10 m，氣孔寬度1 m。入射波周期9～12 s，入射波波幅0.5 m。本研究中計算域長度取10倍波長距離，氣室箱體布置在計算域中間，水槽兩端均布置長度為1.5λ的阻尼層。通過數值收斂性試驗，自由水面上每個波長長度布置20個網格，沿水深方向布置10個網格，時間步長Δt=T/60。圖2(a)、(b)分別給出了入射波周期為12 s和10 s時，透射波高增大率γ隨線性阻尼系數Cdm與二次阻尼系數Ddm變化的對比曲線。從圖中可以看出，本文結果與文獻［7］的數值結果吻合很好。

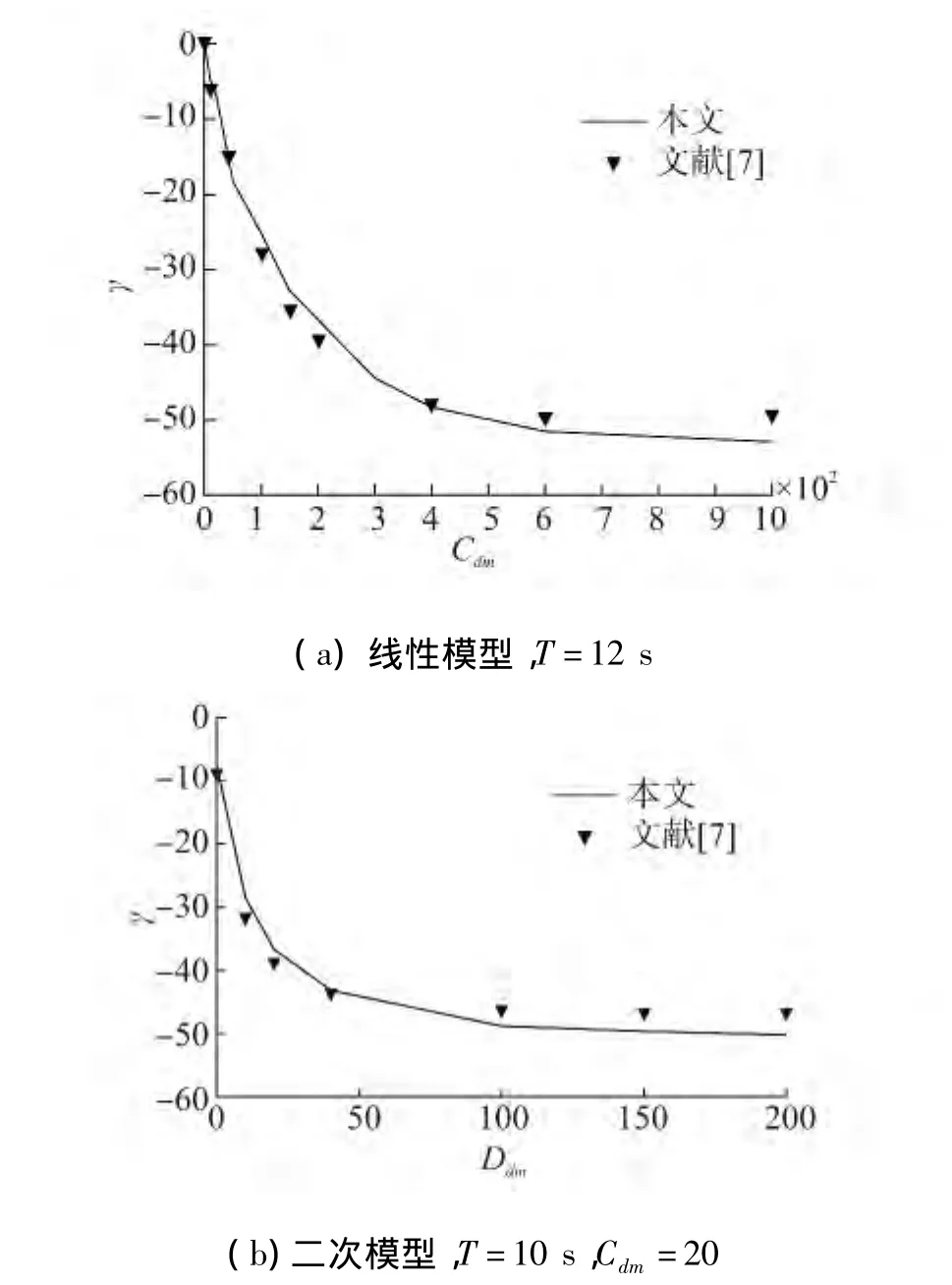
圖2 不同壓強模型的對比Fig.2 Comparison of the pressure models

圖3是線性壓強模型下，Cdm=150，入射波周期T=10 s時防波堤氣室內壓強的時間歷程曲線?？梢钥吹綒馐覂葔簭姴▌又芷谂c入射波周期相同。本模型氣室內的壓強在一定時間后趨于穩定，說明本模型可以消除二次反射的影響進行長時間模擬。

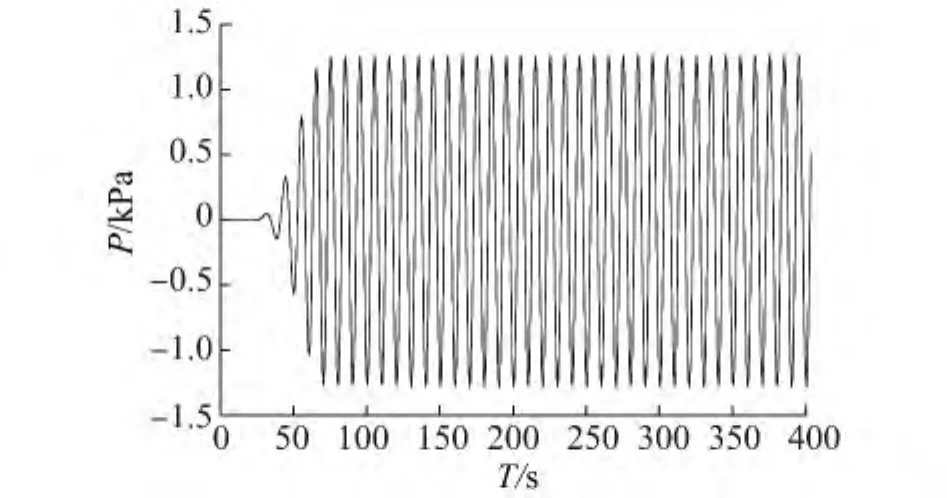
圖3 氣動浮式防波堤氣室內壓強時間歷程，Cdm=150，T=10 sFig.3 Time history of the pressure in the air chamber of pneumatic floating breakwater，Cdm=150，T=10 s

為了進一步驗證數值模型的準確性，將本文結果與文獻［3，9，14］解析解、數值解和實驗值進行了對比。振蕩水柱式波能轉換裝置如圖1，具體參數見表1。氣孔寬度A=0.005 m，計算水深H=0.92 m，入射波幅0.04 m。計算域長度取5倍波長距離，通過開展數值收斂性驗證，單位波長長度內劃分30個網格，時間步長Δt=T/80。本文采用線性壓強模型，經過試算，阻尼系數Cdm選定為 3.5。

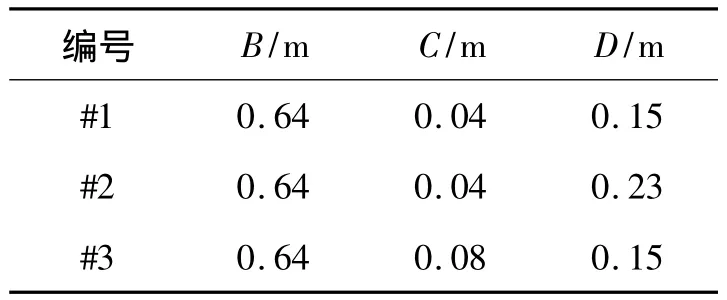
表1 岸式振蕩水柱波能轉換裝置結構尺寸Table 1 Geometrical parameters of the land-based OWC

圖4給出了3種前墻尺寸的波能轉換效率κ隨無量綱入射波周期T*變化的對比結果，T*=從圖中可以看出在高頻區(T*＜6)，3種不同尺寸的模型計算中，本文結果和文獻［9，14］吻合的都較好。在低頻區(T*＞7)，本文結果與文獻［9］的數值結果吻合較好，但與文獻［14］的實驗結果相比數值偏小，可能的原因是在實驗中的造波板與結構距離為37.5 m，在入射波波長較長的情況下二次反射很快會影響到結構處的測量結果，造成能量轉換效率被高估。本文結果與文獻［3］解析解的趨勢和共振頻率基本一致，但數值上有一定差別，這是由于解析解對模型做了很多理想化假定，波能的最大轉化效率可以達到100%，這在實際中是不可能達到的?？傮w來說，相對于文獻［9］的兩相流模型，本模型無論是可計算的頻率寬度還是與實驗結果的對比都較好，具有較高的計算精度。

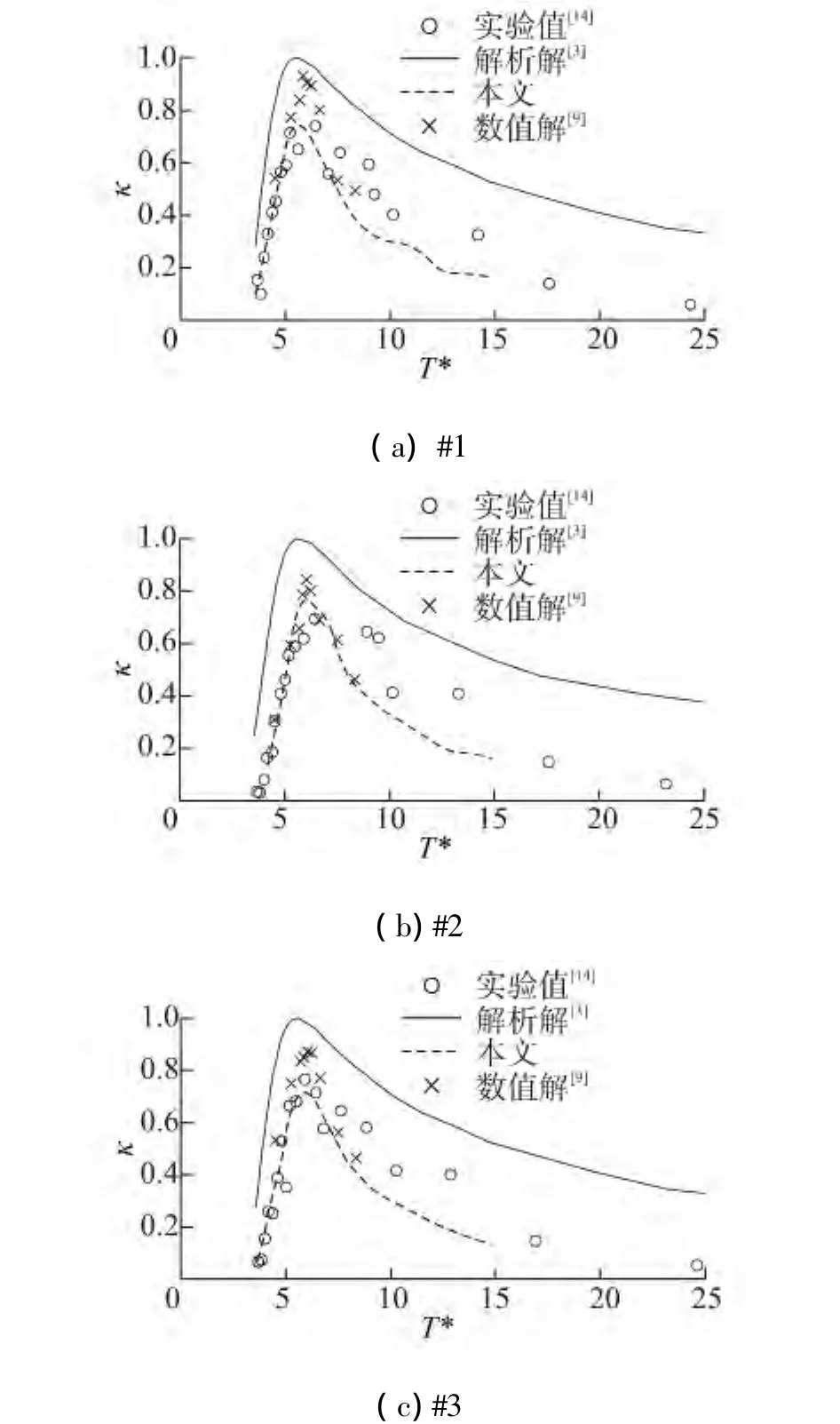
圖4 不同前墻厚度下，能量轉換效率隨無量綱入射周期T*的變化Fig.4 Energy conversion efficiency versus T*with different thickness of the front wall

3 結構尺寸對能量轉換效率的影響

在水深一定的情況下，岸式振蕩水柱波能轉換裝置的前墻入水深度、前墻厚度和氣室寬度是影響其能量轉換效率的主要因素。本文計算水深統一為0.92 m，入射波幅0.04 m。圖5給出了在氣室寬0.64 m，前墻厚度0.04 m時，結構在不同前墻入水深度下的能量轉換效率對比曲線。從圖中可以看到，整個結構存在一個明顯的共振頻率，在此頻率上的能量轉換效率最高，可以達到70%以上。隨著入射波頻率遠離共振頻率，振蕩水柱波能轉換裝置的能量轉換效率逐漸變小。在當前計算范圍內，前墻入水深度的增大會導致結構的共振頻率區間向低頻區域移動，同時高頻區(T*＜6)的能量轉換效率變小，共振頻率上的能量轉換效率增大。前墻入水深度的變化對低頻區(T*＞7)的能量轉換效率影響不大，這是因為在低頻區前墻入水深度相對于波長很小。

圖6給出了氣室寬度0.64 m，前墻入水深度0.15 m情況下，3種不同前墻厚度下的能量轉換效率曲線。同樣，在低頻區(T*＞7)，前墻厚度的變化對能量轉換效率的影響很小。隨著前墻厚度的增大結構的共振區間向低頻區的方向移動，在高頻區和共振頻率上，前墻厚度的增大會導致能量轉換效率的減小。

圖7給出了在前墻入水深度0.15 m，前墻厚度0.04 m，不同氣室寬度下的能量轉換效率對比曲線。改變氣室的寬度會同時改變氣室在低頻區與高頻區的能量轉換效率，隨著氣室寬度的增大結構的共振頻率向低頻方向移動，且能量轉換效率最大值會隨氣室寬度的增大而變小。氣室寬度的增大會改善結構低頻區的能量轉換效率，降低結構在高頻區的能量轉換效率。

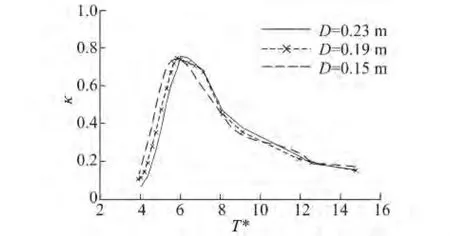
圖5 不同前墻入水深度下，能量轉換效率隨T*的變化Fig.5 Energy conversion efficiency versus T*with different immersion depth of the front wall

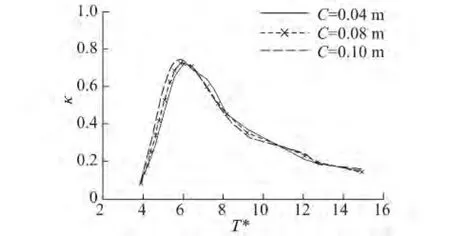
圖6 不同前墻厚度下，能量轉換效率隨T*的變化Fig.6 Energy conversion efficiency versus T*with different thickness of front wall

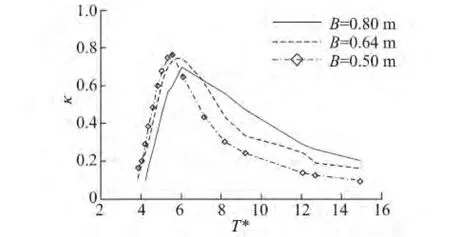
圖7 不同氣室寬度下，能量轉換效率隨T*的變化Fig.7 Energy conversion efficiency versus T*with different width of the chamber

4 結論

本研究利用時域高階邊界元理論與氣體壓強模型建立了岸式振蕩水柱波能轉換裝置的完全非線性數值模型。從研究中可以發現岸式振蕩水柱波能轉換裝置具有一個明顯的共振區間，適當減小前墻入水深度、厚度與氣室寬度都可以增大共振頻率、提高高頻區的能量轉換效率;前墻尺寸的變化對低頻區能量轉換效率的影響十分微小;氣室寬度的增加會提高低頻區的能量轉換效率，降低高頻區的能量轉換效率。和前人的勢流模型相比，本模型采用高階單元與源造波技術，精度更高，所需單元更少且消波問題很容易處理。和粘性流模型相比，本模型的計算效率更高，在合理的阻尼系數下同樣可以與實驗結果吻合良好。由于無法計算由于流動分離、渦旋等引起的粘性耗散并且尚未考慮空氣的可壓縮性，本模型存在一定的局限性，下一步工作需要建立更加貼近實際的壓強模型并考慮粘性耗散的影響，同時對模型進行三維拓展，以達到更好的模擬效果。

［1］EVANS D.The oscillating water column wave-energy device［J］.IMA Journal of Applied Mathematics，1978，22(4):423-433.

［2］游亞戈.復雜地形下岸式波能裝置的水動力學計算［J］.海洋技術，1993，12(1):20.YOU Yage.Hydrodynamic calculation of shore-mounted wave-power device at complicated topography［J］.Ocean Tecnology，1993，12(1):20.

［3］EVANS D，PORTER R.Hydrodynamic characteristics of an oscillating water column device［J］.Applied Ocean Research，1995，17(3):155-164.

［4］DELAUR Y，LEWIS A.3D hydrodynamic modelling of fixed oscillating water column wave power plant by a boundary element methods［J］.Ocean Engineering，2003，30(3):309-330.

［5］WANG D，KATORY M，LI Y.Analytical and experimental investigation on the hydrodynamic performance of onshore wave-power devices［J］.Ocean Engineering，2002，29(8):871-885.

［6］HONG D，HONG S Y，HONG S W.Numerical study of the motions and drift force of a floating OWC device［J］.Ocean Engineering，2004，31(2):139-164.

［7］KOO W，KIM M，LEE D.Nonlinear time-domain simulation of pneumatic floating breakwater［J］.International Journal of Offshore and Polar Engineering，2006，16(1):25-32.

［8］KOO W，KIM M-H.Nonlinear time-domain simulation of a land-based oscillating water column［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，2010，136(5):276-285.

［9］ZHANG Y，ZOU Q P，GREAVES D.Air-water two-phase flow modelling of hydrodynamic performance of an oscillating water column device［J］.Renewable Energy，2011，41:159-170.

［10］劉臻.岸式振蕩水柱波能發電裝置的試驗及數值模擬研究［D］.青島:中國海洋大學，2008:70-107.LIU Zhen.Experimental and numerical investigation of oscillating water column wave energy converter［D］.Qingdao:Ocean University of China，2008:70-107.

［11］紀君娜，劉臻，紀立強.振蕩水柱波能發電裝置氣室的三維數值模擬研究［J］.海岸工程，2011，30(2):7-13.JI Junna，LIU Zhen，JI Liqiang.3D numerical simulation for oscillating water column chamber in wave-power converter［J］.Coastal Engineering，2011，30(2):7-13.

［12］SARMENTO A，FALCAO A F O.Wave generation by an oscillating surface-pressure and its application in wave-energy extraction［J］.Journal of Fluid Mechanics，1985，150:467-485.

［13］TSENG R S，WU R H，HUANG C C.Model study of a shoreline wave-power system［J］.Ocean Engineering，2000，27(8):801-821.

［14］MORRIS-THOMAS M T，IRVIN R J，THIAGARAJAN K P.An investigation into the hydrodynamic efficiency of an oscillating water column［J］.Journal of Offshore Mechanics and Arctic Engineering，2007，129(4):273-278.

［15］NING D，TENG B，EATOCK T R，et al.Numerical simulation of non-linear regular and focused waves in an infinite water-depth［J］.Ocean Engineering，2008，35(8):887-899.

［16］NING D，TENG B.Numerical simulation of fully nonlinear irregular wave tank in three dimension［J］.International Journal for Numerical Methods in Fluids，2007，53(12):1847-1862.