大口徑平衡炮內彈道一維兩相流建模與仿真

張博孜,王 浩,王珊珊,曹仁義

(1.南京理工大學 能源與動力工程學院,南京 210094;2.中國工程物理研究院 流體物理研究所,四川 綿陽 621900)

導彈武器的研發過程需要大量試射試驗的支撐,而試射試驗的高成本性是制約導彈武器發展的重要因素。炮射導彈方式可有效降低試驗成本,但受導彈口徑大、動能高、火炮反后座裝置體積龐大甚至無法工作的限制,平衡炮在此背景下得到了大力發展[1]。平衡炮利用平衡體與彈丸的反向運動替代傳統火炮的反后座裝置,使平衡體與彈丸同時脫離炮口,以保證炮身自身動量為零。這種設計思想可在保證彈丸高動能前提下省去專門的火炮反后座裝置,從而最大限度地簡化發射裝置[2]。

國內目前建成或在建的大口徑平衡炮已多達數門,但對平衡炮內彈道過程的仿真研究多局限于零維模型。文獻[3]中基于拉格朗日假設討論了平衡炮膛內的壓力分布,但與兩相流模型相比,零維模型所描述的物理過程仍不夠全面。

平衡炮一般采用大藥室、大弧厚、大藥量的管狀藥模塊化裝填方式,其具體形式如圖1所示。長管狀藥能明顯改善火藥透氣性,盡量避免因火藥堆積造成的壅塞現象;模塊化的裝填方式則最大限度地保證了點火初期火藥排列有序的狀態,對改善點傳火特性具有十分重要的意義。

圖1 平衡炮裝藥結構示意圖

傳統火炮裝藥多采用粒狀藥,單顆粒狀藥的特征尺寸遠小于火炮藥室,且粒狀藥的長徑比不大,因此在內彈道兩相流建模時可將固相火藥顆粒假設成流體。對于火藥長徑比較小的情況,可以采用此假設,如文獻[1]采用此法分析了平衡炮膛內壓力波的發展規律。而由多個長管狀藥束首尾相連組成的平衡炮主裝藥床,在隔板、中心點火管等結構的支撐下,相比傳統火炮裝藥更具整體性。當彈丸和平衡體開始運動后,主裝藥床的左右兩端都會出現較大的自由空間,藥床在膛內壓力梯度作用下會沿軸向運動,但藥床不易解體,形成火藥顆粒堆積于某一端的狀態。在這種情況下將膛內的固相火藥假設成流體已不再合適。本文提出一種不將固相流體化,而是將氣固兩相分別考慮的平衡炮內彈道一維兩相流模型,依此編制計算程序進行數值仿真,并結合320 mm平衡炮的試驗數據進行對比分析,為驗證模型的可行性提供支撐,也為進一步深入研究平衡炮內彈道過程奠定基礎。

1 數理模型的建立

兩相流體動力學是研究火炮等身管武器內彈道過程的最重要理論之一。兩相流模型建立的準確與否很大程度上決定著數值仿真結果的準確性。

1.1 基本假設

針對平衡炮模塊化裝藥的特點,在計算時可將膛內劃分成3個區域:氣相區、固相區(包括整個發射藥床的可燃支撐結構)和傳火管內的氣固混合區。氣固混合區主要針對傳火管內的黑火藥,其計算獨立于整個發射藥床,但其軸向位置取決于發射藥床的位置。根據這種思路提出以下主要假設:

①由于將氣、固兩相分開考慮,則不再將發射藥床流體化,而是將發射藥床整體看作一個變質量的剛體運動,其受力情況和運動規律主要由藥床兩端燃氣壓力和氣固兩相間阻力決定。

②由于裝藥模塊之間的支撐結構都開有足夠大的透氣孔,因此可不考慮其對燃氣流動的影響;支撐結構雖為可燃物,但其能量與裝藥量和點火藥量相比均可忽略,因此不考慮支撐結構的燃燒產物。

③由于傳火管內采用燃速較快的黑火藥,且點火方式為多點點火,可認為黑火藥瞬間燃完,其能量釋放規律由小孔流量公式確定[4]。

④固相區生成的質量、動量和能量以及傳火管內釋放的能量均作為“源”項加入氣相區。

⑤認為同一截面上氣相壓力、溫度、密度等物理量在管狀藥內外無差別。

⑥由于40/1管狀藥長徑比超過20,可以忽略管狀藥的端面燃燒。

1.2 一維兩相流數學模型

1.2.1 守恒形式氣相控制方程組

(1)

式中:

(2)

(3)

(4)

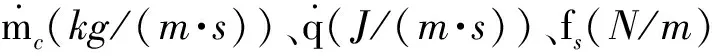
1.2.2 固相運動方程

基于基本假設,將固體火藥床看成一個變質量的剛體,在氣固兩相交換物理量時需知道火藥床的運動速度vp和位置l以及質量mp,其運動規律和燃燒規律由運動方程、質量方程和燃燒方程來描述。

火藥床整體運動的主要動力來源是火藥燃氣對固體火藥表面的相間阻力之和∮fsdx,以及火藥床兩端面所受壓力fa和fb。根據牛頓第二定律可給出火藥床運動方程:

(5)

(6)

mp=mp0-(mg+ml)

(7)

式中:mp0為火藥床的初始總質量。火藥床減少的質量由主裝藥已燃質量mg和點火藥已燃質量ml組成。管狀藥束按幾何燃燒定律燃燒,燃速方程采用指數公式,即

(8)

(9)

式中:re0,ri0分別為單根管狀藥初始外徑和內徑;re,ri分別為任意時刻管狀藥外徑和內徑;μ1,n分別為管狀藥燃速系數和燃速指數。以mg為例,任意時刻主裝藥已燃質量為

(10)

式中:c1為單根管狀藥長度,N為當前位置管狀藥束的根數。

1.2.3 輔助方程

1)氣體狀態方程[5]。

(11)

式中:α為火藥燃氣余容,一般取0.001 m3/kg;R為氣體常數,火藥氣體一般取值1.24。

2)相間阻力方程。

考慮管狀發射藥通氣性好且排列有序,文獻[6]推薦采用以下阻力公式:

(12)

fs=Cf[A0(1-φ)/dp](vg-vp)|vg-vp|ρg=Cf(An/dp)(vg-vp)|vg-vp|ρg

(13)

式中:Cf為阻力系數;φ為當地空隙率,可由身管截面積和管狀藥束截面積求得;dp為火藥當量直徑。

3)火藥表面溫度方程。

(14)

式中:Tps,T0,Tg分別為火藥表面溫度、初溫和燃氣溫度;h為放熱系數;導溫系數a1=9.19×10-8m2/s;λp為導熱系數,取λp=0.083 74 W/(m·s·K)。

4)相間熱交換方程。

(15)

式中:qc,qr分別為單位時間內單位火藥表面積對流換熱量和輻射換熱量;Cn為藥床截面周長。其中:

qc=h(Tg-Tps)

(16)

(17)

式中:εp為顆粒表面灰度,取值0.85;σ為斯忒藩-玻爾茲曼常數,取σ=5.656 94×10-8J/(s·m2·K4)。

5)彈丸和平衡體運動方程。

(18)

(19)

式中:v1,v2分別為彈丸、平衡體速度;A1,A2分別為彈底和平衡體底面積;pd1,pd2分別為彈底和平衡體底壓力;m1,m2,φ1,φ2分別為彈丸和平衡體的質量和次要功系數。

2 數值計算方法

2.1 差分格式

采用內彈道仿真較成熟的Mac-Cormack格式計算,格式如下。

預估步:

(20)

校正步:

(21)

此格式采用CFL穩定性條件。

2.2 初邊條件

初始計算條件由具體裝填條件確定。彈丸和平衡體啟動前的彈底邊界條件按鏡面反射法給出,啟動后的邊界條件按運動控制體法計算。

2.3 網格劃分

2.3.1 重疊網格技術

針對平衡炮發射藥床整體運動這一假設,本文采用重疊網格技術。即對氣相而言,在計算域內劃分軸向一維網格,除彈底和平衡體底部網格隨彈丸、平衡體運動外,其余網格固定不動;對發射藥床單獨劃分一維網格,網格固聯于藥床;兩相間需要交換的質量、動量、能量或其它物理量均按位置差值而得,如圖2所示。

圖2 網格劃分示意圖

2.3.2 動網格技術

彈丸(平衡體)的運動會造成彈底網格的變形,從而造成計算結果的失真。本文采用適合結構動網格的動態層法,即在彈底網格變形超過一定變形率ε后增加一個網格,ε一般取0.5倍網格空間步長[7]。

3 數值計算與試驗結果對比分析

以上述數學物理模型為基礎,本文數值模擬了320 mm平衡炮2種不同裝藥量的內彈道全過程,2種裝藥量分別為90 kg、138 kg,發射藥分裝于6個模塊,彈丸、平衡體質量均為450 kg和2 500 kg。

實彈試驗中測試點的位置如圖2所示,其中測點1位于藥室靠近平衡體一端;位置2介于藥室和彈丸出口之間;位置3是彈丸出口處的壓力測試點,此處壓力曲線的上升沿表示彈丸已經出炮口,是內彈道過程結束的標志。

圖3給出了90 kg和138 kg裝藥量位置1計算、測試壓力-時間對比曲線;圖4為90 kg和138 kg裝藥量位置2的計算、測試壓力-時間對比曲線。表1列出了主要計算與測試結果,表中,mp0為裝藥質量,vp和vd分別表示平衡體和彈丸的初速。

圖3 位置1壓力-時間對比曲線

圖4 位置2壓力-時間對比曲線

圖3表明,2種裝藥量情況下位置1的壓力曲線符合較好,壓力峰值與測試值基本一致。圖4中位置2的曲線上升沿時刻與測試值基本相同,證明計算得到的彈丸初期運動規律比較準確。圖4中,位置2曲線上升沿后的壓力峰值出現了偏差,導致該現象的原因可能是實際發射中由于發射藥床靠近彈丸一端,此時存在較明顯的碎裂現象,致使燃氣生成速率短時間內升高。位置3的曲線上升沿作為內彈道過程結束的標志,也基本和計算結束在同一時刻。由此看來,通過將發射藥看作整體運動的藥床,分別計算氣固兩相間的質量、動量和能量的方式描述平衡炮內彈道過程,能夠得到與試驗符合較好的結果。

表1 試驗結果與計算結果對比

4 結束語

本文針對大口徑平衡炮模塊化裝藥的特點,建立了不同于傳統兩相流中將固相流體化的內彈道模型。該模型更接近于大口徑平衡炮的模塊化裝填條件。采用該模型和重疊網格技術對320 mm平衡炮進行了數值計算,計算結果與炮射試驗結果符合良好,證明了該模型的有效性,并且驗證了重疊網格技術在內彈道兩相流計算中的可行性。

平衡炮的大口徑化是其發展的必然趨勢,大弧厚、長管狀藥模塊化裝填亦是目前最有效安全的裝藥方式。本文的建模思路正是針對這種變化對傳統平衡炮兩相流模型帶來的挑戰,這種思路也對其它大口徑平衡炮內彈道過程研究具有指導意義。

[1] 徐流恩.李永池,高樂南.大口徑高速平衡炮不同發射藥應用探討[J].彈道學報,2009,21(2):15-18.

XU Liu-en,LI Yong-chi,GAO Le-nan.The application discussion of propellant in large caliber and high speed counter-mass propelling gun[J].Journal of Ballistics,2009,21(2):15-18.(in Chinese)

[2] 談樂斌,侯保林,陳衛民.降低火炮后坐力技術概述[J].火炮發射與控制學報,2006(4):69-72.

TAN Le-bin,HOU Bao-lin,CHEN Wei-min.Gun recoil force reduction technology[J].Journal of Gun Launch & Control,2006(4):69-72.(in Chinese)

[3] 彭換新.平衡炮膛內壓力分布分析[J].南京工業職業技術學院學報,2005,5(2):28-31.

PENG Huan-xin.Analysis of pressure distribution in chamber of gun for balance[J].Journal of Nanjing Institute of Industry Technology,2005,5(2):28-31.(in Chinese)

[4] 季曉松,王浩,馮國增,等.高炮口動能大口徑火炮中多點點火技術試驗研究[J].彈道學報,2010,22(4):67-69.

JI Xiao-song,WANG Hao,FENG Guo-zeng,et al.Experimental research on technology of multi-point ignition in large caliber gun with high muzzle energy[J].Journal of Ballistics,2010,22(4):67-69.(in Chinese)

[5] 翁春生,王浩.計算內彈道學[M].北京:國防工業出版社,2006.

WENG Chun-sheng,WANG Hao.Computational interior ballistics[M].Beijing:National Defense Industry Press,2006.(in Chinese)

[6] 周彥煌,王升晨.實用兩相流內彈道學[M].北京:兵器工業出版社,1990.

ZHOU Yan-huang,WANG Sheng-chen.Applied two-phase flow interior ballistics[M].Beijing:Ordnance Industry Press,1990.(in Chinese)

[7] 金志明,袁亞雄,宋明.現代內彈道學[M].北京:北京理工大學出版社,1992.

JIN Zhi-ming,YUAN Ya-xiong,SONG Ming.Modern interior ballistics[M].Beijing:Beijing Institute of Technology Press,1992.(in Chinese)