BP神經網絡和Cox比例風險模型在生存分析應用中的比較*

李文琦，黃水平，李海朋

徐州醫學院公共衛生學院流行病與衛生統計學教研室 徐州 221002

BP神經網絡和Cox比例風險模型在生存分析應用中的比較*

李文琦，黃水平#，李海朋

徐州醫學院公共衛生學院流行病與衛生統計學教研室 徐州 221002

#通訊作者，女，1963年10月生，碩士，教授，研究方向：統計方法在流行病學研究中的應用，E-mail：hsp@xzmc.edu.cn

BP神經網絡；Monte Carlo 模擬；生存分析；預測模型；Cox比例風險模型

目的：比較BP神經網絡模型和Cox比例風險模型在生存分析中的預測性能，進一步探討BP神經網絡模型在生存分析中的應用。方法采用Monte Carlo模擬數據集，如不同樣本量、不同刪失比例、不同協變量間關系及是否滿足等比例風險假定的理論研究和胃癌根治術患者預后預測的實例分析，分別建立BP神經網絡模型和Cox比例風險模型，最終使用一致性指數C對其預測性能進行比較。結果當樣本量為100、刪失比例為60%、80%及樣本量為300、刪失比例為80%時，BP神經網絡模型的預測性能高于Cox比例風險模型(P<0.05)。協變量不滿足等比例風險假定、協變量間存在三維交互作用和非線性關系時，BP神經網絡模型的預測性能較Cox比例風險模型好(P<0.05)。實例研究中發現，BP神經網絡模型預測的一致性指數C(0.835)高于Cox比例風險模型(t配對=4.311，P<0.001)。結論BP神經網絡模型在生存分析的應用中對樣本刪失比例、是否滿足PH假定、協變量間復雜交互作用和非線性關系具有非特異性，對資料限制較少，且預測一致性高，值得在生存分析中進一步推廣應用。

目前生存分析最常用的即Cox比例風險模型，但該模型要求資料事先滿足2個假定[1]：①比例風險假定(proportional hazard, PH假定)。②對數線性假定。然而當實際資料不能滿足或只能近似滿足這一假定時，往往會造成模型擬合效果不佳或者根本沒有意義，最終還會誤導人們對分析結果的判斷，而人工神經網絡模型恰恰彌補了這方面的不足。近年來，人工神經網絡作為一種新興的信息處理系統，具有自組織、自適應、自學習的能力及高度的非線性和良好的容錯性等特點，被廣泛地應用于多個領域，特別在流行病學領域也逐漸受到重視[2]。但國內人工神經網絡模型的應用尚不成熟，特別是在生存分析領域的應用還比較分散，多用于解決某個具體問題。目前尚缺乏對人工神經網絡模型與傳統的生存分析方法比較的系統研究，故作者采用Monte Carlo模擬的理論研究和實際資料的應用研究相結合的方法，比較BP神經網絡模型和Cox比例風險模型在生存分析中的預測性能，以探討人工神經網絡模型在生存分析領域中的應用，為生存分析領域提供一種不考慮模型具體函數形式的非線性預測手段，以達到較好地解決實際問題的目的。

1 模擬實驗方法及實例資料

1.1模擬實驗設計模擬數據包括：不同樣本量、不同刪失比例和不同協變量間的關系及協變量是否滿足等比例風險假定等條件。

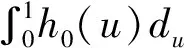
根據上式可模擬不同分布的生存時間，最終可實現生存數據的產生。

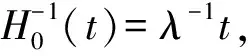
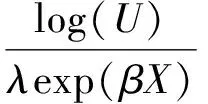
模擬非比例風險假定的數據則采用對數正態回歸模型產生生存時間，T=exp(1+βx+ε)。

1.1.2 模擬刪失數據 該研究模擬產生右刪失數據，刪失分布的類型為均勻分布U(0,C)。模擬時首先產生n(n為樣本量)個生存時間Ti，根據刪失分布U(0,C)及刪失比例，通過迭代模擬，計算出C值，再通過SAS的隨機數產生程序，產生n個刪失時間Li。最后根據右刪失的定義，ti=min(Ti,Li)，得到n個觀測時間。若Ti≤Li,δi=1，否則，即產生含刪失的生存數據(ti,δi)[3]。

1.1.3 模擬協變量 用SAS隨機數發生器RANNOR(seed)函數產生服從N(0,1)標準正態分布隨機變量,用RANBIN(seed,n,p)函數產生服從B(n,p)的伯努利分布隨機變量。

1.2模擬評價指標由于該研究2種方法的預測變量不同，且存在刪失數據，故采用一致性指數C作為預測準確性評價的指標。一致性指數C是指預測結果和實際結果一致的觀察單位對子數占總有用對子數的比例。有用對子數是指可區分危險度大小的2個個體，若兩者都達到觀察終點，或一個達到終點，而另一個為刪失個體，并刪失個體的觀察時間大于非刪失個體的觀察時間，以上2種可度量危險度大小關系的情況被認為是有用的觀察對子。并用SAS對2種方法的一致性指數C進行配對t檢驗，檢驗水準α=0.05。

1.3實例資料

1.3.1 研究對象 選取2004年1月1日至2009年12月30日于徐州醫學院附屬醫院行胃癌根治性切除術且經病理學確診并有詳細聯系方式的胃癌患者156例。

1.3.2 隨訪調查 自2009年12月至2010年5月，采用電話訪問及信訪的方式追蹤研究對象。以患者手術之日為研究起點，因胃癌死亡為研究終點，隨訪截止時間為2010年5月14日。

1.3.3 調查內容 臨床資料包括：研究對象的腫瘤部位、大小、浸潤深度、分化程度、組織學分型、是否伴有淋巴結轉移、pTNM分期等。生活資料包括：研究對象的飲食、生活行為方式及心理因素等。主要有每天蔬菜水果和肉蛋類的攝入量、是否服用營養補充劑和中草藥、體育鍛煉頻度、睡眠狀況、吸煙飲酒習慣等生活行為方式，患者性格、恢復的信心及煩躁、焦慮、恐慌等心理狀況和其社會支持等。

2 結果

2.1不同樣本量和刪失比例下模型的預測性能比較模擬符合如下條件的生存數據：生存時間服從λ=1的指數分布，協變量x1服從N(0,1)的正態分布、x2服從B(1,0.8)的伯努利分布，樣本量為100和300、刪失比例分別為20%、40%、60%和80%的數據集。

Cox比例風險模型：設x1、x2回歸系數分別為β1=1、β2=1.5，并計算線性預測之和xβ′進行預測；BP神經網絡模型：由2個協變量作為BP神經網絡模型輸入神經元(即n=2)，以CSR作為BP神經網絡輸出神經元(即l=1)，選擇LM優化算法和適當的隱含層結點數，其余參數均為Matlab軟件默認值，最終使網絡達到收斂。每種模擬樣本重復模擬100次，得一致性指數C的均數和標準差，見表1。

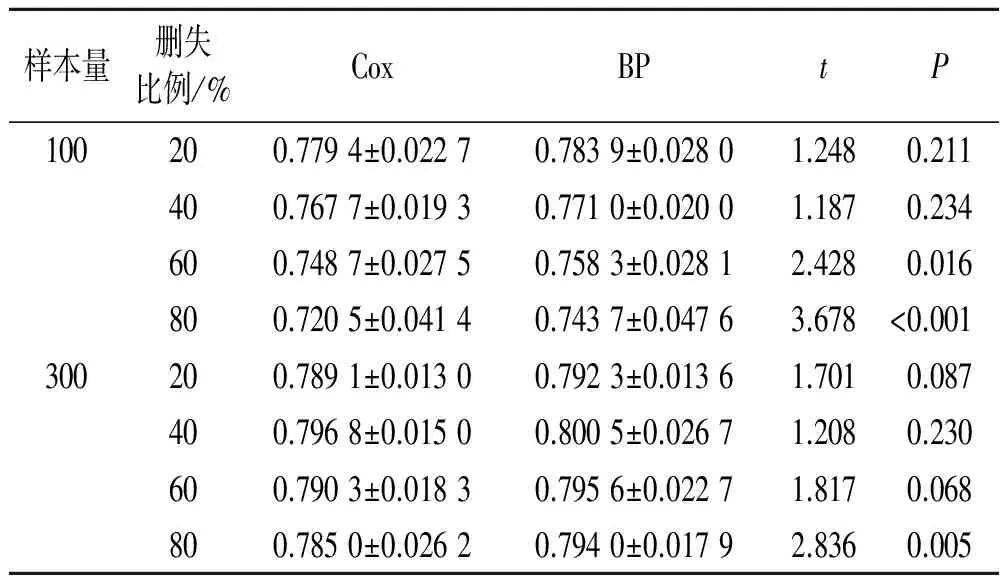
表1 不同樣本量和刪失比例下兩模型一致性指數C的比較

2.2等比例、非等比例風險及不同協變量關系下模型的預測性能比較模擬符合如下條件的生存數據：樣本量固定為300，刪失比例為40%。生存時間服從l=1的指數分布(滿足PH假定)和對數正態分布(不滿足PH假定)。分別設計以下幾種不同協變量間關系的數據集：

①滿足PH假定，協變量間獨立：協變量x1服從N(0,1)的正態分布、x2服從B(1,0.8)的伯努利分布，Cox比例風險模型x1、x2的回歸系數分別為β1=1和β2=1.5。

②滿足PH假定，協變量間存在二維交互：設x1和x2間存在r12=0.2二維交互作用，其余同①。

③滿足PH假定，協變量間存在多維交互：模擬4個協變量，協變量x1和x2分別服從B(1,0.25)和B(1,0.5)的伯努利分布，x3和x4均服從N(0,1)的正態分布，設Cox比例風險模型x1、x2、x3、x4的回歸系數分別為b1=b2=2、b3=0.5、b4=1.0，二維交互作用，x1和x2及x3和x4的相關系數分別為r12=r34=1.0，其他三維交互r′=0.5。

④滿足PH假定，協變量間存在非線性關系：模擬協變量x1服從N(0,1)的正態分布，對x1進行非線性轉換得到x2=sigmoid(x1)，設Cox模型x1、x2的回歸系數分別為b1=1和b2=1.5。

⑤不滿足PH假定，協變量間相互獨立：協變量設計同①。

每次模擬重復100次，得一致性指數C的均數和標準差，見表2。

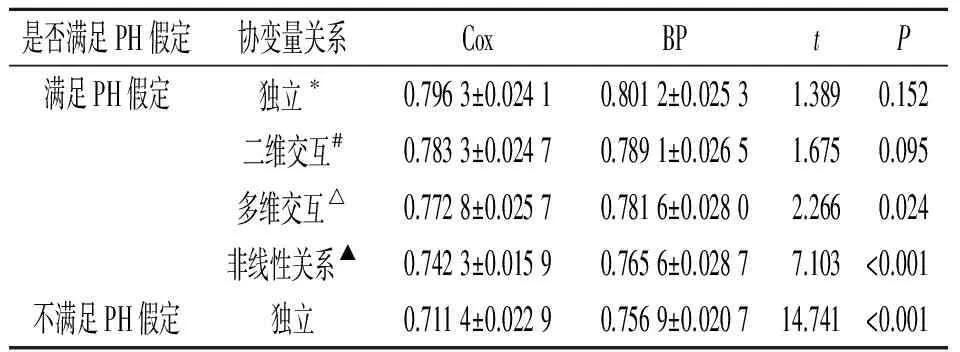
表2 不同PH假定及協變量關系下模型一致性指數C的比較

*：h(t/x)=h0(t)exp(1.0x1+1.5x2)；#：h(t/x)=h0(t)exp(1.0x1+1.5x2+0.2x1x2)；

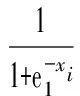
2.3實例分析結果隨機選取100例胃癌根治術患者作為模型的訓練樣本，建立Cox比例風險模型，首先進行單變量log-rank時序檢驗，其次將有統計學意義的因素進一步做多因素Cox回歸分析，建立胃癌根治術患者預后預測的Cox比例風險模型，其表達式為：h(t,x)=h0(t)exp(0.814 3x1+1.004x2+0.579x3-0.932x4-0.585x5-1.199x6)，式中x1、x2、x3、x4、x5、x6分別代表pTNM分期、分化程度、腫瘤大小、是否接受輔助化療、睡眠狀況和術前吸煙術后不吸煙6個因素。最終將其余56例作為預測樣本，代入已建立的模型進行預測性能的評價。

選擇3層網絡結構，將6個對生存時間有影響的因素作為網絡輸入神經元，以Cox-snell殘差為輸出神經元，根據試湊法最終確定隱含層結點數為8，隱含層傳輸函數為tansig，輸出層傳輸函數為purelin。學習率為0.01，網絡訓練采用LM優化算法，為防止過度擬合，采用早停止策略。2種模型建模重復20次，得一致性指數C的均值、標準差，見表3。配對t檢驗結果顯示，BP神經網絡模型的預測一致性指數C高于Cox比例風險模型(t配對=4.311,P<0.001)。

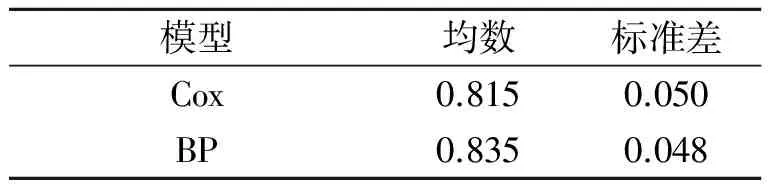
表3 Cox模型和BP模型的預測一致性指數C

3 討論

有研究[4]表明Cox模型結果的偏倚程度隨刪失比例的增大而增大，且增大速度和樣本量有關。Cox模型準確性也會隨著刪失比例的增大而減小，且當刪失超過70%時，結果變異加速增大。該研究模擬了樣本量為100的小樣本和樣本量為300的大樣本2個數據集。選擇小樣本數據時，當刪失比例超過60%時，Cox模型的一致性指數C減小,與BP神經網絡模型預測一致性指數C比較差異均有統計學意義；在大樣本情況下，當刪失比例超過80%時，Cox模型一致性指數C急劇下降，與BP神經網絡模型預測一致性指數C比較差異均有統計學意義，進一步說明BP神經網絡模型在同等數據的刪失比例下預測一致性指數C高于Cox模型。

理論已證明神經網絡對變量間關系信息的提取具有非特異性，該模擬試驗中對線性和非線性及多維的復雜交互作用進行的模擬研究也說明了這一點，在變量間存在非線性關系時BP神經網絡模型預測的一致性指數C高于Cox模型。在Cox模型中對變量有一嚴格的限制，要求協變量的效應不隨時間而改變，即滿足等比例風險假定。在不滿足假定的條件下使用Cox模型建模得出的結果將讓人產生質疑。故作者對是否滿足PH假定條件的協變量進行了模擬，分別用BP神經網絡模型和Cox模型建模，發現在不滿足PH假定時BP神經網絡模型預測的一致性指數C要好于Cox模型。由此可以看出，BP神經網絡模型克服了傳統統計分析方法對數據的嚴格限制，可以不考慮數據間關系的具體函數形式，任意連續的S型函數理論上都能得到較好的擬合效果。因此，BP神經網絡模型與傳統的統計方法相比，它不需要精確的數學模型，沒有任何對變量的假定要求，能通過模擬人的智能行為處理一些復雜的、不確定的、非線性的問題，且具有一定的容錯性。其處理非線性問題的能力一般高于傳統的分析方法，并且可以學習目前無法用數學方法描述的模糊評定。它為處理模糊的、數據不完全的、模擬的、不精確的模式的識別提供了一個全新的途徑，在醫學領域有進一步推廣的價值。

[1]王娟.截尾分位數回歸模型及其在生存分析中的應用[D].太原:山西醫科大學,2009．

[2]高蔚,施侶元.人工神經網絡流行病學應用進展[J].中華預防醫學雜志,2000,34(6):373

[3]Cox DR，Oakes D. Analysis of survival data[M]. London：Chapman and Hall，1984:201

[4]錢俊.生存分析中刪失數據比例對Cox回歸模型影響的研究[D].廣州:南方醫科大學,2009:95

(2014-01-17收稿 責任編輯姜春霞)

Comparison between BP neural network and Cox proportional hazard model in survival analysis

LIWenqi,HUANGShuiping,LIHaipeng

DepartmentofEpidemiologyandMedicalStatistics,SchoolofPublicHealth,XuzhouMedicalCollege,Xuzhou221002

BP neural network; Monte Carlo simulation; survival analysis; forecast model; Cox proportional hazard model

Aim: To compare their prediction performance of BP neural network model and Cox proportion hazard model in survival analysis and to explore the superiority of BP neural network model in survival analysis. Methods: Monte Carlo was used to generate the data sets under the condition of different sample size, different degree of censoring, number of variable and interactions, non-linear effect, distinct distribution of covariate and proportional vs non-proportional hazard. Then BP neural network model and Cox model were built, and their prediction performance was compared using concord ance index C. Results: In the research on simulation data sets, when the sample size of 100, proportion of censoring of 60%, 80%, and sample size of 300, proportion of censoring of 80%, BP neural network model performed superior to Cox model(P<0.05). And when the covariates don′t meet PH assumption and had three-way interaction, non-linear effect, BP neural network performed superior to Cox model(P<0.05). In the real data, BP neural network model′s concordance index was 0.835, which performed superior to Cox model(tpaired=4.311,P<0.001). Conclusion: For the small sample size, high and the covariates don′t meet PH assumption and has three-way interaction, non-linear effect data sets, BP neural network has better advantage than Cox model. It is worth to popularize further in survival analysis.

10.13705/j.issn.1671-6825.2014.06.015

*江蘇省科技廳資助項目 BE2011647

R195.1