轉速數對滑動軸承動力學系數影響研究

馬文生, 陳照波, 焦映厚, Kirk R G

(1.中航工業沈陽發動機設計研究所，沈陽 110015；2.哈爾濱工業大學 機電工程學院，哈爾濱 150001；3.弗吉尼亞理工大學 轉子動力學實驗室，美國 24061)

在旋轉機械中，轉子-軸承系統存在油膜力、密封力等非線性激振力，導致系統存在不穩定的因素。軸承的參數變化對轉子的動力學特性有明顯的影響，由于軸承是阻尼的主要來源，進而控制著轉子的響應；軸承的剛度和阻尼又影響著轉子-軸承系統的臨界轉速和穩定性。所以在深入研究轉子-軸承系統動力學問題時，必須考慮軸承對系統的作用[1-2]。謝友柏等[3]研究非線性油膜力和軸承外彈性阻尼對流體動壓滑動軸承轉子系統的振動特性的影響，建立了非線性運動方程式, 并開發了相關程序。袁小陽、朱均[4-5]基于周期解計算的打靶法和Floquet穩定性理論,給出了轉子-軸承系統不平衡激勵周期解及其穩定性非線性分析的數值方法，并用此方法研究了剛性轉子-圓柱軸承系統中不平衡量對穩定性的影響。焦映厚和陳照波等[6-8]應用精度高、速度快的非線性油膜力數據庫方法及非線性動力系統的穩定性和分叉理論對轉子-軸承系統進行了分析，數值計算得到了轉子- 軸承系統發生倍周期分叉時的分叉點及分叉圖，揭示了不平衡轉子-軸承系統從同步周期運動分叉發生一系列倍周期運動、最后導致混沌運動的過程。

本文以滑動軸承為研究對象，基于流體動力潤滑控制方程推導出滑動軸承的Reynolds方程。利用DyRoBes軟件[9-10]對決定軸承承載力的油膜壓力進行計算及比較，分析并計算了不同的轉速下的偏心率、最小油膜厚度、最大油膜壓力、摩擦功耗、溫升、臨界軸頸質量、剛度系數、阻尼系數等影響滑動軸承油膜特性及動力學行為的重要參數。最后，在分析三維油膜壓力時發現存在一個臨界轉速，當轉速低于某個臨界值時臨界轉速對最大油膜壓力影響較大。

1 滑動軸承油膜力模型

滑動軸承由軸頸和軸瓦組成，軸頸一般比軸瓦的直徑小0.1%～0.2%。軸頸和軸瓦之間存在一定的間隙，使得潤滑油進入間隙形成油膜，由于流體的動壓力產生了足夠的承載力，并且循環的潤滑油流過間隙起到降溫作用，避免溫度過高保證軸承正常工作[2,11]。

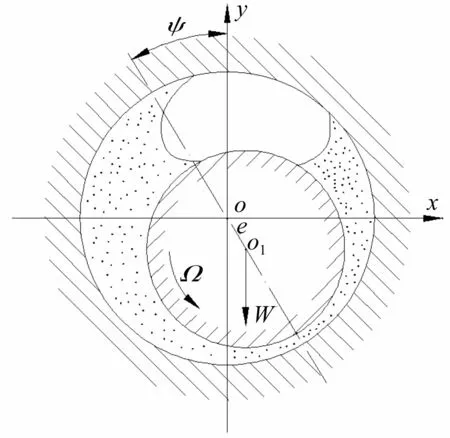
圖1 軸頸的靜平衡位置

圖2 油膜厚度與油楔

圖1是軸頸的靜平衡位置圖，其中o是軸瓦中心，o1是軸頸中心，W是靜載荷，Ω是軸頸轉速，e是偏心距，C是軸承的半徑間隙，偏心率ε=e/C，ψ是偏位角，h是油膜厚度，ζ是從y軸順時針方向的轉角，靜平衡位置由偏心距和偏位角決定。

油膜厚度和油楔如圖2所示，圖中最大油膜厚度和最小油膜厚度為：

hmax=C+e=C(1+ε)

hmin=C-e=C(1-ε)

(1)

任意位置的油膜厚度為：

h=C+ecos(ζ-ψ)=C[1+εcos(ζ-ψ)]

(2)

Reynolds方程是軸承油膜分析的基本方程：

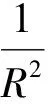
(3)

其中：R是軸頸半徑，p是油膜壓力，η是潤滑油粘度，z是軸瓦軸向坐標；

軸承分析的步驟一般為：通過Reynolds方程求解油膜的壓力分布p(ζ,z)，然后求軸承的靜特性系數(最小油膜厚度、最大油膜壓力、摩擦功耗、潤滑油流量、溫升、承載力、軸頸運動軌跡等)和動力特性系數。

對于無限短軸承L?D，這樣油膜力周向比軸向變化率小很多[12]，即?p/?φ??p/?λ，這樣Reynolds方程(3)的左端的周向函數可以忽略不計，因此Reynolds方程簡化為：

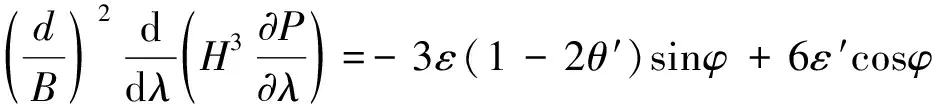
邊界條件：

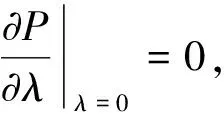
油膜力極坐標表達式：

(6)

極坐標無量綱表達式為：

(7)

則無量綱油膜力直角坐標表達式為：

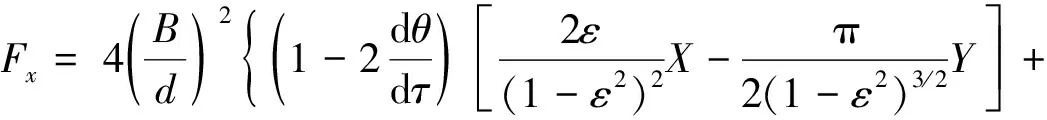
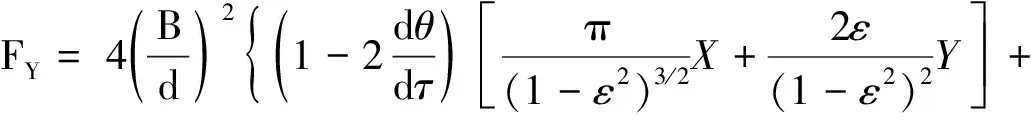
(8)

2 滑動軸承靜、動特性系數影響因素研究

2.1 滑動軸承模型建立

軸承長度l=125 mm，軸承半徑R=125 mm，軸頸間隙h=0.5 mm，潤滑粘度系數μ=47×10-3Pa/s，計算轉速3 000 r/min～12 000r/min，靜載荷500 kg，通過DyRoBes-BePerf建模如圖3所示：

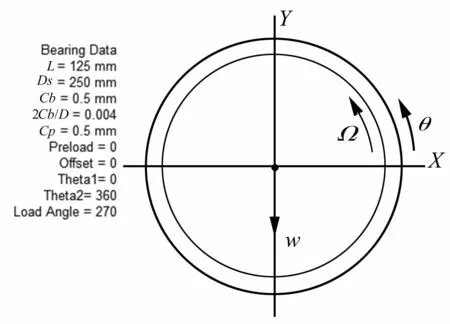
圖3 軸承模型

2.2 轉速對滑動軸承靜、動力學特性影響研究

圖4是轉速對軸承動力學特性影響，其中包括轉速對偏心率、最小油膜厚度、最大油膜壓力、摩擦功耗、溫升、臨界軸頸質量、剛度系數和阻尼系數的影響研究。

圖4(a)是當存在一個固定載荷W時，軸頸轉速從1 000 r/min增大到12 000 r/min時轉速對偏心率的影響研究，表明隨著轉速的增大偏心率減小，軸頸中心O′逐漸趨向于軸瓦中心O；圖4(b)是轉速對最小油膜厚度的影響，隨著轉速的增大最小油膜厚度增大，這是因為隨著轉速增大，軸頸中心朝著軸瓦中心運動，從而使得最小油膜厚度增大；圖4(c)是轉速對最大油膜壓力的影響，圖中可以看到轉速從1 000 r/min增大到4 800 r/min時，最大油膜壓力迅速減小，當轉速大于4 800 r/min時最大油膜壓力變化不大；圖4(d)是轉速對摩擦損耗的影響，從圖中可以看到，隨著轉速的增大摩擦損耗逐漸增大，并且增大頻率越來越大。

圖4 轉速對軸承動力學特性影響

圖4(e)是轉速對臨界軸頸質量的影響，當轉速從1 000 r/min增大到4 800 r/min時軸頸臨界質量迅速減小，當轉速大于4 800 r/min時軸頸臨界質量變化不大；圖4(f)是入口溫度、工作溫度和最大溫度隨轉速的變化，圖中可以看到隨著轉速的增大軸承工作溫度增大；圖4(g)是轉速從1 000 r/min到12 000 r/min的主剛度和主阻尼的值，圖中可以看到轉速小于3 000 r/min時主剛度和主阻尼變大明顯，當轉速大于3 000 r/min時主剛度和主阻尼變化不大；圖4(h)是轉速從1 000 r/min到12 000 r/min的交叉剛度和交叉阻尼的值，圖中虛線為負值，Kxy隨著轉速的增大而增大，Kyx隨著轉速的增大而負向增大，Cxy和Cyx相等并且隨著轉速的增大而減小。

圖5 軸頸運動軌跡

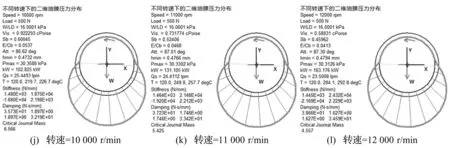
圖6 不同轉速下的二維油膜壓力分布

圖7 不同轉速下的三維油膜壓力分布

圖5是軸頸運動軌跡圖，圖中可以看到隨著轉速從1 000 r/min增大到12 000 r/min時，軸頸中心向軸瓦中心移動。圖6是不同轉速下的二維油膜壓力分布，從圖6(a)～6(l)可以看到，隨著轉速的增大軸頸中心會隨之變化，當轉速為1 000 r/min時最小油膜厚度為0.183 2 mm，當轉速增大到5 000 r/min時最小油膜厚度增大到0.428 3 mm，當轉速增大到12 000 r/min時最小油膜厚度增大到0.479 4 mm；同時油膜壓力分布和油膜壓力幅值都有著顯著的變化。

為了進一步得出油膜壓力分布情況，本文進行計算了轉速1 000 r/min到轉速12 000 r/min共計12種三維油膜壓力分析，并相應得出三維油膜壓力的俯視圖和切片圖，如圖7所示。圖7(a)可以看到，當轉速為1 000 r/min時偏心率為0.633 5，最大油膜壓力為44.278 kPa；圖47(e)為轉速5 000 r/min時最大油膜壓力分布圖，此時偏心率為0.143 4，從圖中可以看到最大油膜壓力為30.714 5 kPa；圖7(h)為轉速8 000 r/min時最大油膜壓力分布圖，此時偏心率為0.073 9，從圖中可以看到最大油膜壓力為30.431 4 kPa；圖7(l)為轉速12 000時，此時偏心率為0.041 3，最大油膜壓力為30.312 6 kPa。通過以上分析得到：隨著轉速的增大，最大油膜壓力減?。淮嬖谝粋€臨界轉速5 000 r/min，當轉速小于5 000 r/min時，增大轉速時最大油膜壓力會有較大變化；當轉速大于5 000 r/min時，偏心率小于0.1，轉速再增大只會引起偏心率微弱減小，最大油膜壓力也會有微弱減小。最大油膜壓力存在5 000 r/min臨界轉速原因：偏心率越大油膜壓力越大，轉速越大則偏心率越小，所以轉速的增大會導致最大油膜壓力的減??；對于本文模型，當轉速為1 000 r/min時偏心率為0.633 5，而當轉速增大到5 000 r/min時偏心率迅速減小到0.073 9，轉速變化使得偏心率減小了0.559 6，而當轉速從5 000 r/min增大到12 000 r/min偏心率只減小了0.032 6，偏心率是最大油膜壓力的重要影響因素，偏心率的較大變化會引起油膜壓力的較大、反之偏心率的較小變化也會使得最大油膜壓力變化較小，分析結果與本文計算結果一致。

3 結 論

(1)本文建立了滑動軸承的動力學模型，并對其進行求解；

(2)研究轉速對滑動軸承動力學特性進行研究，得到了轉速對偏心率、最小油膜厚度、最大油膜壓力、摩擦功耗、溫升、臨界軸頸質量、剛度系數、阻尼系數、二維和三維油膜壓力的影響因素研究；

(3)在對三維油膜壓力分析時發現存在一個臨界值，當轉速低于某個臨界值時臨界轉速對最大油膜壓力影響較大，當轉速高于這個臨界值時臨界轉速對最大油膜壓力影響不大。

參 考 文 獻

[1]黃文虎，夏松波，焦映厚.旋轉機械非線性動力學設計基礎理論與方法[M].北京:科學出版社，2006.

[2]鐘一諤,何衍宗,王 正,等.轉子動力學[M].北京:高等教育出版社, 1987.

[3]謝友柏，湯玉娣,夏松波. 具有非線性油膜力的滑動軸承轉子系統振動特性研究[J]. 西安交通大學學報，1987，21(4)：93-104.

XIE You-bai, TANG Yu-di, XIA Song-bo. Influence of non-linearity of hydrodynamic oil film forces on vibration characteristics of journal bearing-rotor system [J]. Journal of Xi’an Jiaotong University, 1987, 21(4):93-104.

[4]袁小陽，朱 均. 不平衡轉子-滑動軸承系統穩定性的非線性研究[J]. 振動與沖擊，1996，15(1)：71-77.

YUAN Xiao-yang, ZHU Jun. Study on the non-linear stability of unbalance rotor bearing system [J]. Journal of vibration and shock, 1996, 15(1): 71-77.

[5]朱 均，虞 烈. 流體潤滑理論[M]. 西安交通大學出版社，1986.

[6]焦映厚，李明章，陳照波. 不同油膜力模型下轉子-圓柱軸承系統的動力學分析[J]. 哈爾濱工業大學學報，2007，39(1)：46-50.

JIAO Ying-hou, LI Ming-zhang, CHEN Zhao-bo. Dynamic analysis of rotor-cylindrical bearing system with different oil film force models[J]. Journal of Harbin Institute of Technology, 2007，39(1)：46-50.

[7]陳照波，焦映厚,陳 明,等.非線性轉子-軸承系統動力學分叉及穩定性分析[J]. 哈爾濱工業大學學報，2002，34(5)：587-590.

CHEN Zhao-bo, JIAO Ying-hou, CHEN Ming, et al. Dynamic bifurcation and stability analysis for nonlinear rotor bearing system[J]. Journal of Harbin Institute of Technology,2002, 34(5): 587-590.

[8]焦映厚，陳照波,夏松波，等.轉子-非圓軸承系統非線性動力學行為的研究[J]. 航空動力學報，2000，15(6)：413-418.

JIAO Ying-hou,CHEN Zhao-bo, XIA Song-bo, et al. Study on nonlinear dynamic behavior of rotor-non-circular bearing system[J]. Journal of Aerospace Power, 2000, 15(6): 413-418.

[9]Kirk R G, Alsaeed A, Gunter E J. Stability analysis of a high-speed automotive turbocharger[J]. Tribology Transactions, 2007,50,3:427-434.

[10]Kirk R G, Alsaeed A, Liptrap J, et al. Experimental test results for vibration of a high speed diesel engine turbocharger[J]. Tribology Transactions, 2008,51(4):422-427.

[11]張 文.轉子動力學理論基礎[M].北京:科學出版社,1990.

[12]張直明,張言羊,謝友柏.滑動軸承的流體動力潤滑理論[M].北京:高等教育出版社,1987.