具有強對稱自同態的環及其擴張
王 堯,薛 嶺,任艷麗
(1.南京信息工程大學 數學與統計學院,南京 210044; 2.南京曉莊學院 數學與信息技術學院,南京 211171)
(1-α(1))α(1)=1·(1-α(1))α(1)=0
(r1,s1)+(r2,s2)=(r1+r2,s1+s2), (r1,s1)(r2,s2)=(r1r2+s1r2+s2r1,s1s2),
具有強對稱自同態的環及其擴張
王 堯1,薛 嶺1,任艷麗2
(1.南京信息工程大學 數學與統計學院,南京 210044; 2.南京曉莊學院 數學與信息技術學院,南京 211171)
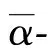
強α-對稱環; 強α-可逆環; 強α-半交換環;α-compatible環; 經典右商環; 斜多項式環
0 引 言
設本文討論的環R均為有單位元的結合環,α是環R的一個非零自同態.如果對任意的r∈R,由rα(r)=0可推出r=0,則稱環R的一個自同態α為rigid同態[1].如果α是環R的rigid同態,則稱環R是α-rigid環.如果R沒有非零冪零元,則稱環R是約化環.如果對任意的a,b∈R,由ab=0可推出ba=0,則稱環R是可逆環[2].如果對任意的a,b∈R,由ab=0可推出bα(a)=0(α(b)a=0),則稱環R的一個自同態α是右(左)可逆的[3].如果α是環R的右(左)可逆同態,則稱環R是右(左)α-可逆的.如果環R既是右α-可逆環,也是左α-可逆環,則稱環R是α-可逆環.如果對任意的a,b∈R,由aα(b)=0(α(a)b=0)可推出ba=0,則稱環R的一個同態α是強右(左)可逆的[4].如果α是環R的強右(左)可逆同態,則稱環R是強右(左)α-可逆環.如果環R既是強右α-可逆環,也是強左α-可逆環,則稱環R是強α-可逆環.強α-可逆環是α-可逆環,但α-可逆環未必是強α-可逆環,可逆環也未必是強α-可逆環[4].如果對任意的a,b∈R,由ab=0可推出aRb=0,則稱環R是半交換環.對任何a,b∈R,如果由ab=0可推出aRα(b)=0(α(a)Rb=0),則稱環R是右(左)α-半交換環[5].
如果對任意的a,b,c∈R,由abc=0可推出acb=0,則稱環R是對稱環[6].Anderson等[7]證明了環R是對稱環的等價條件是對任意的r1,r2,…,rn∈R(n≥2),由r1r2…rn=0可推出rσ(1)rσ(2)…rσ(n)=0,其中σ∈Sn.如果對任意的a,b,c∈R,由abc=0可推出acα(b)=0(α(b)ac=0),則稱環R的自同態α是右(左)對稱的[8].如果α是環R的右(左)對稱同態,則稱環R是右(左)α-對稱環.如果環R既是左α-對稱環,也是右α-對稱環,則稱環R是α-對稱環.對于環R的一個自同態α,如果對任意的a,b,c∈R,由abα(c)=0可推出acα(b)=0,則稱環R是對稱α-環.上述各環間的關系是:α-rigid環?α-對稱環?α-可逆環.逆向命題均不成立.
本文考慮滿足如下假設條件的環:
(H1) 對任意的a,b,c∈R,由abα(c)=0可推出acb=0.
命題1如果環R是一個α-rigid環,則環R滿足假設條件(H1).
證明: 設abα(c)=0,a,b,c∈R,則有cabα(c)α(ab)=0,cabα(cab)=0.因為環R是α-rigid環,所以有cab=0.因為α-rigid環是對稱環,從而可推出acb=0.
可見存在滿足假設條件(H1)的環.下面舉例說明滿足假設條件(H1)的環與α-對稱環是不同的概念.
例1設Z2為二元域,R=Z2⊕Z2.對于環R和R的自同態α:R→R,α((a,b))=(a,0),如果(a1,b1)(a2,b2)(a3,b3)=0,則有(a1,b1)(a3,b3)α((a2,b2))=0,且有α((a2,b2))(a1,b1)(a3,b3)=0.于是R是一個α- 對稱環.但環R和自同態α不滿足假設條件(H1),因為(1,1)(0,1)α(1,1)=(0,0),而(1,1)(1,1)(0,1)=(0,1)≠(0,0).
1 強α-對稱環
定義1設R是一個環,α是R的一個自同態.如果對任意的a,b,c∈R,由abα(c)=0(α(a)bc=0)可推出acb=0(bac=0),則稱α是強右(左)對稱的.如果α是環R的強右(左)對稱的自同態,則稱環R是強右(左)α-對稱環.如果環R既是強右α-對稱環,也是強左α-對稱環,則稱環R是強α-對稱環.
顯然,如果環R是對稱環,則環R是一個強IdR-對稱環,其中IdR表示環R的恒等自同態.設α是環R的一個自同態,R是強α-對稱環.命題1表明α-rigid環是強右α-對稱環.如果S是環R的一個子環且滿足α(S)?S,則S也是強α-對稱環.
命題2如果一個環R是強右(左)α-對稱環,則環R是對稱環.
證明: 設環R是強右α-對稱環.如果abc=0,a,b,c∈R,則有1·α(ab)α(c)=α(abc)=0,即cα(a)α(b)=0.于是又有1·cbα(a)=0,從而有acb=0.因此環R是對稱環.
如果環R是一個強左α-對稱環且有abc=0,a,b,c∈R,則有α(a)α(bc)·1=α(abc)=0,α(b)(α(c)a)·1=0.可推出α(c)ab=0,從而有acb=0.同理可推出環R是對稱環.
命題2表明強右(左)α-對稱環是對稱環的一個子類.下面舉例說明當α≠IdR時,一個對稱環未必是強右(左)α-對稱環.
例2設Z2是二元域,R=Z2⊕Z2,則環R是對稱環.對于R的自同態α:R→R,α((x,y))=(y,x)和a=(1,1),b=(1,0)=c,有abα(c)=0,但acb=(1,0)≠0,故R不是一個強右α-對稱環.
推論1設α是環R的一個自同態,則R是強右α-對稱環當且僅當R是強左α-對稱環.
證明: 設R是強右α-對稱環,α(a)bc=0,a,b,c∈R.因為環R是對稱環,所以有bcα(a)=0,從而有bac=0,故R也是強左α-對稱環.反之亦然.
推論1表明強左α-對稱環與強右α-對稱環是同一個概念,于是可對這兩個概念不加區分,統稱為強α-對稱環.
命題3設α是環R的一個自同態,如果R是強α-對稱環,則有以下結論:
1)α是單同態;
2)α(1)=1;
3)α(e)=e,其中e是環R的冪等元.
證明: 1) 任取a,b∈R,如果α(a)=α(b),則有1· 1·α(a-b)=0.由R是強α-對稱環可得a-b=0,故α是單同態.
2) 因為(1-α(1))α(1)=0,所以由R是強α-對稱環知1-α(1)=0,即α(1)=1.
3) 因為(1-e)e=e(1-e)=0,所以由R是強α-對稱環得α(e)(1-e)=α(1-e)e=0,即α(e)=α(e)e=e.
對于環R的一個自同態α,如果對任意的a,b∈R,ab=0當且僅當aα(b)=0,則稱環R是α-compatible的[9].
引理1[9]環R是一個α-rigid環當且僅當R是α-compatible的和約化的.
如果對任意的a∈R,由aRa=0可推出a=0,則稱環R是半素環.
由命題1和推論1可知,α-rigid環是強α-對稱環.進一步, 有:
命題41) 環R是α-rigid環當且僅當R是強α-對稱環和約化環;
2) 環R是α-rigid環當且僅當R是強α-對稱環且是半素環.
證明: 1) 必要性.根據引理1知α-rigid環是約化環.再據命題1和推論1即得結論.
充分性.設rα(r)=0,r∈R,則由R是強α-對稱環有r2=1·rα(r)=0,再由R是約化環知r=0.
2) 由約化環是半素環及1)即知.
下面給出強α-對稱環和α-compatible環之間的關系.
定理1環R是強α-對稱環當且僅當R是對稱環,且是α-compatible環.
證明: 必要性.如果環R是強α-對稱環,由命題2知環R是對稱環.下證強α-對稱環是α-compatible環.任取a,b∈R,設ab=0.因為R是對稱環,從而是可逆環,于是由ab=0 有ba=0和α(b)·1·α(a)=α(ba)=0.因為R是強α-對稱環,所以有α(b)a=0,于是有aα(b)=0.反之,任取a,b∈R,設aα(b)=0,由環R是有1的強α-對稱環得ba=0.又因為環R是可逆環,所以ab=0.從而證明了環R是α-compatible環,且R是對稱環.
充分性.如果環R是對稱環且是α-compatible環.設abα(c)=0,a,b,c∈R.因為環R是α-compatible環,所以abc=0.同時由R也是對稱環可推出acb=0.于是知環R是強α-對稱環.
定理2設α是環R的一個自同態,R是一個α-compatible環,則以下結論等價:
1)R是強α-對稱環;
2)R是α-對稱環;
3)R是對稱α-環;
4)R是對稱環.
證明: 由文獻[10]中定理3.5和定理2.8即知.
引理2[9]如果R是α-compatible環,則有下列結論:
1) 如果ab=0,則aαn(b)=an(a)b=0,其中n是任意正整數;
2) 如果存在正整數k,使得αk(a)b=0,則ab=0;
3) 如果存在正整數k,使得aαk(b)=0,則ab=0.
推論2如果環R是強α-對稱環,則對任意的a1,a2,a3∈R和非負整數i,j,k,對任何σ∈Sn,a1a2a3=0當且僅當αi(aσ(1))αj(aσ(2))αk(aσ(3))=0.
證明: 由定理1和引理2可得.
下面給出強α-對稱環的一些等價刻畫.
定理3設α是環R的一個自同態,則下列結論等價:
1) 環R是強α-對稱環;
2) 環R是α-對稱環且α是一個單同態;
3) 環R是對稱的且是α-可逆環,α是一個單同態;
4) 環R是強α-可逆且R是對稱的;
5) 環R是對稱α-環且R是對稱的,α是一個單同態.
證明: 如果一個環是強α-對稱環,則α是一個單同態,R是對稱環.由推論2,有1)?2),1)?3)和1)?5)成立.
1)?4).設aα(b)=0(α(a)b=0).由1·aα(b)=0(α(a)b·1=0)及強α-對稱環的定義,有ba=0.
2)?1).任取a,b,c∈R,設abα(c)=0,即1·abα(c)=0.由R是右α-對稱環可推出1·α(cab)=0.因為α是一個單同態,所以cab=0.而根據文獻[8]中定理2.5知,如果環R是右α-對稱環且α是一個單同態,則R是對稱環.于是有acb=0.
3)?1).任取a,b,c∈R,設abα(c)=0.由R是右α-可逆環可推出α(cab)=0.因為α是一個單同態,所以cab=0.因為R是對稱的,所以acb=0.
4)?1).任取a,b,c∈R,設abα(c)=0.由R是強α-可逆環推出cab=0.因為R是對稱的,所以acb=0.
5)?1).任取a,b,c∈R,設abα(c)=0.已知R是對稱α-環且α是單同態,則由
(1-α(1))α(1)=1·(1-α(1))α(1)=0
可得1·1·α(1-α(1))=α(1-α(1))=0,于是有1-α(1)=0,α(1)=1.又因為R是有1的對稱環,所以還有α(c)abα(1)=0.再由R是對稱α-環知α(c)·1·α(ab)=0,從而α(cab)=0.由α是單同態知cab=0.由環R是對稱環可得acb=0.
定義2設α是環R的一個自同態.如果對任意的a,b∈R,由aα(b)=0(α(a)b=0)可推出aRb=0,則稱α是強右(左)半交換的.如果α是環R的強右(左)半交換的自同態,則稱環R是強右(左)α-半交換環.如果環R既是強右α-半交換環,也是強左α-半交換環,則稱環R是強α-半交換環.
命題5環R是強α-對稱環當且僅當R是對稱環,且是強α-半交換環.
證明: 必要性.由命題2知強α-對稱環是對稱環,而強α-對稱環是強α-半交換環.
充分性.設abα(c)=0,α(a)bc=0,a,b,c∈R.因為R是強α-半交換環,所以有abRc=0和aRbc=0.因為R有1,故可推出abc=0.再由R是對稱環有acb=0.
命題61) 強α-半交換環是α-半交換環; 2) 強α-半交換環是半交換環.
證明: 1) 設ab=0,a,b∈R,則有α(ab)=α(a)α(b)=0.因為R是強α-半交換環,所以有aRα(b)=0和α(a)Rb=0.
2) 因為R有1,故有α(a)b=aα(b)=0.再由R是強α-半交換環,可得aRb=0.
2 強α-對稱環的擴張




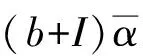
命題9設α是環R的一個自同態,e是環R的中心冪等元且有α(e)=e,則下列結論等價:
1)R是強α-對稱環;
2)eR和(1-e)R是強α-對稱環.
證明: 1)?2).設環R是強α-對稱環.因為eR,(1-e)R是環R的子環,且α(eR)?eR,α((1-e)R)?(1-e)R,所以eR,(1-e)R都是強α-對稱環.
2)?1).因為R是eR和(1-e)R的直和,強α-對稱環的直和也是強α-對稱環.因此,R也是強α-對稱環.

引理4[11]設R是約化環,n是任意一個正整數,則R[x]/(xn)是對稱環,其中(xn)是由xn生成的理想.

證明: 根據定理3中4)知,環R是強α-對稱環當且僅當R是強α-可逆環,且R是對稱環,再由引理3和引理4可得結論.證畢.
對于任何環R和整數n≥2.令


證明: 根據文獻[12],Vn(R)?R[x]/(xn).


推論5[11]如果R是約化環,則T(R,R)是對稱環.
命題5指出了α-rigid環R的平凡擴張T(R,R)是強α-對稱環,但文獻[4]中例3.6表明,n階主對角線元素相同的上三角陣環不是強右α-可逆環,從而也不是強α-對稱環(n≥3).


證明: 由R是Δ-1R的子環知充分性成立.
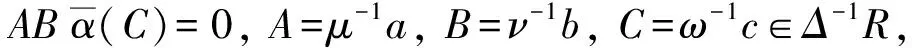

從而abα(c)=0.而環R是強α-對稱環,于是有acb=0.進一步,有
ACB=μ-1aω-1cν-1b=μ-1ω-1ν-1(acb)=0.

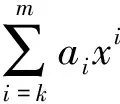



推論6設α是環R的自同態,如果環R是Armendariz環,則下列結論等價:
1)R是強α-對稱環;


證明: 由命題12知,2)?3).2)?1)顯然.1)?2): 根據定理3中4)知,環R是強α-對稱環當且僅當R是強α-可逆環,且R是對稱環.由文獻[4]中定理3.7知,如果環R是強α-可逆環且R是Armendariz環,則R[x]是強α-可逆環.再由文獻[14]中命題3.2知,如果環R是對稱環且R是Armendariz環,則R[x]是對稱環.

證明: 充分性顯然.下證必要性.

于是有如下等式:
由式(1)得a0b0c0=0.將式(2)左乘b0c0,由R為約化環得b0c0a1α(b0)α2(c0)=0,再據推論2和R為約化環有a1b0c0=0,a1α(b0)α2(c0)=0.將式(2)再左乘c0,重復應用推論2和R為約化環的條件,有c0a0b1α2(c0)=0.于是有a0b1c0=0,a0b1α2(c0)=0. 代入式(2)可得a0b0c1=0.所以當i+j+k=1時,有aibjck=0.
歸納假設當i+j+k 將式(p+1)右乘a0b0,由歸納假設可推出a0b0cp=0.將式(p+1)左乘b0c0,由推論2可得apb0c0=0.于是,式(p+1)變為 進一步,將式(p+2)右乘a0b1,由歸納假設可得a0b1cp-1=0, 在式(p+3)右邊繼續分別乘以a0b2,a0b3,…,ap-1b1,則由歸納假設和推論2依次可得a0b2cp-2=0,a0b3cp-3=0,…,ap-1b1c0=0. 命題13設α是環R的自同態,如果S是一個環,且σ:R→S是環同構,則環R是強α-對稱環當且僅當S是強σασ-1-對稱環. 證明: 充分性.設S是強σασ-1-對稱環,abα(c)=0,a,b,c∈R,則有σ(a)σ(b)σασ-1(σ(c))=σ(abα(c))=0.因為S是強σασ-1-對稱環,所以σ(acb)=σ(a)σ(c)σ(b)=0.而σ是一個環同構,于是有acb=0,因此環R是強α-對稱環. 必要性.由充分性證明可知. 命題14設A是環R相應的Jordan擴張,則環R是強α-對稱環當且僅當A是強α-對稱環. 證明: 由R是環A的子環知充分性成立. 必要性.設abα(c)=0,其中a,b,c∈A,則存在n≥0,使得αn(a),αn(b),αn(c)∈R.于是有αn(a)αn(b)α(αn(c))=αn(abα(c))=0.由環R是強α-對稱環可知αn(acb)=αn(a)αn(c)αn(b)=0.因為α是環A的同構,所以有acb=0.從而A是強α-對稱環. 給定交換環S上的代數R,R通過S的Dorroh擴張是Abel群D=R⊕S,其運算如下: (r1,s1)+(r2,s2)=(r1+r2,s1+s2), (r1,s1)(r2,s2)=(r1r2+s1r2+s2r1,s1s2), 證明: 充分性顯然. s1s2s3=0,r1r2α(r3)+s1r2α(r3)+s2r1α(r3)+s1s2α(r3)+s3r1r2+s3s1r2+s3s2r1=0. 因為S是無零因子環,所以有s1=0或s2=0或s3=0.如果s1=0,則有 r1r2α(r3)+s2r1α(r3)+s3r1r2+s3s2r1=0. 因為環R是交換的且α(1)=1,所以 于是由R是強α-對稱環可得r1(r3+s3)(r2+s2)=0,即有 r1r3r2+r1r3s2+r1s3r2+r1s3s2=0. 因此 [1]Krempa J.Some Examples of Reduced Rings [J].Algebra Colloq,1996,3(4): 289-300. [2]Cohn P M.Reversible Rings [J].Bull London Math Soc,1999,31(6): 641-648. [3]Baser M,Hong C Y,Kwak T K.On Extened Reversible Rings [J].Algebra Colloq,2009,16(1): 37-48. [4]Baser M,Kwak T K.On Strong Reversible Rings and Their Extensions [J].Korean J Math,2010,18(2): 119-132. [5]Baser M,Harmanci A,Kwak T K.Generalized Semicommutative Rings and Their Extensions [J].Bull Korean Math Soc,2008,45(2): 285-297. [6]Lambek J.On the Representation of Modules by Sheaves of Factor Modules [J].Canad Math Bull,1971,14: 359-368. [7]Anderson D D,Camillo V.Semigroups and Rings Whose Zero Products Commute [J].Comm Algebra,1999,27(6): 2847-2852. [8]Kwak T K.Extensions of Extended Symmetric Rings [J].Bull Korean Math Soc,2007,44(4): 777-788. [9]Hashemi E,Moussavi A.Polynomial Extensions of Quasi-Baer Rings [J].Acta Math Hungar,2005,107(3): 207-224. [10]張玖琳,王堯,任艷麗.關于α-shifting環,α-sy環和α-sc環 [J].數學理論與應用,2013,33(3): 15-21.(ZHANG Jiulin,WANG Yao,REN Yanli.Onα-Shifting Rings,α-sy Rings andα-sc Rings [J].Math Theory Appl,2013,33(3): 15-21.) [11]Huh C,Kim K K,Kim N K,et al.Basic Examples and Extensions of Symmetric Rings [J].J Pure Appl Algebra,2005,202(1/2/3): 154-167. [12]Lee T K,ZHOU Yiqiang.Armendariz and Reduced Rings [J].Comm Algebra,2004,32(6): 2287-2299. [13]Rege M,Chhawchharia S.Armendariz Rings [J].Proc Japan Acad Ser A Math Sci,1997,73(1): 14-17. [14]WANG Zhanping.Extensions of Symmetric Rings [J].J Math Res Expos,2007,27(2): 229-235. [15]Pourtaherian H,Rakhimov I S.On Skew Version of Reversible Rings [J].Inter J Pure Appl Math,2011,73(3): 267-280. (責任編輯: 趙立芹) RingswithStronglySymmetricEndomorphismsandTheirExtensions WANG Yao1,XUE Ling1,REN Yanli2 The rings with strongly symmetric endomorphisms were investigated.Letαbe an endomorphism of ringR.RingRis known as strong rightα-symmetric ifabα(c)=0 impliesacb=0 for anya,b,c∈R.The relationships between strongα-symmetric ring and symmetric,strongα-reversible or strongα-semicommutative ring were discussed,and some extensions of strongα-symmetric rings were studied.It is proved that 1) RingRis strongα-symmetric if and only ifRis symmetric andα-compatible; 2) RingRis strongα-symmetric if and only ifR[x;α] is strongα-symmetric; 3) Ifαis an automorphism of right Ore ringR,thenRis strongα-symmetric if and only if the classical right quotient ringQ(R) ofRis strongα-symmetric. strongα-symmetric ring; strongα-reversible ring; strongα-semicommutative ring;α-compatible ring; classical right quotient ring; skew polynomial ring 2014-01-13. 王 堯(1962—),男,漢族,博士,教授,從事環論、 微分代數和代數表示論的研究,E-mail: wangyao@nuist.edu.cn.通信作者: 任艷麗(1965—),女,漢族,碩士,教授,從事環論的研究,E-mail: renyanlisx@163.com. 國家自然科學基金(批準號: 11101217)和江蘇省自然科學基金(批準號: BK20141476). O153.3 A 1671-5489(2014)05-0861-08





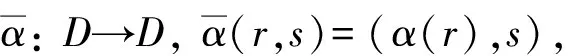



(1.SchoolofMathematicsandStatistics,NanjingUniversityofInformationScienceandTechnology,Nanjing210044,
China; 2.SchoolofMathematicsandInformationTechnology,NanjingXiaozhuangUniversity,Nanjing211171,China)

