大規模氣泡湮滅的元胞自動機模擬

胡亞軍,閆廣武

(吉林大學 數學學院,長春 130012)

大規模氣泡湮滅的元胞自動機模擬

胡亞軍,閆廣武

(吉林大學 數學學院,長春 130012)

使用元胞自動機模型,并用正六邊蜂房結構代替二維均勻氣泡,模擬氣泡載荷超過臨界載荷時大規模二維氣泡湮滅過程. 結果表明,該過程存在Zipf律.

元胞自動機; 二維氣泡; Zipf律

自Bak等[1-2]提出自組織臨界概念以來,人們已經發現這種現象具有某種普適性,如地震、 森林火災、 雪崩和河流的形成等都是自組織臨界的[3-5]. 研究表明,對于臨界的自組織系統,當能量均勻緩慢地連續加入系統中時,所引起的能量耗散是突然的、 雪崩式的； 而對于處于臨界狀態的系統,存在一個表示頻率與尺度關系的對數直線關系,即遵從Zipf律,分形結構即為這樣的系統. 自組織臨界系統還有很多,如對于水的成核汽化相變,大規模氣泡湮滅中可能存在自組織臨界現象. 基于此,本文應用元胞自動機模型,模擬處于臨界狀態的氣泡破裂過程. 用正六角形的蜂房結構(實際是正六角形的內切圓)代替均勻氣泡. 外界能量的加入采用選定氣泡的微小重量增加,研究臨界重量與氣泡破裂數的關系. 結果表明,該過程是自組織臨界的.

1 元胞自動機模型

元胞自動機(cellular automata,又稱細胞自動機,點格自動機,簡稱CA)是空間、 時間和狀態變量完全離散的動力系統[6]. 許多相同的元胞(即點格)以均勻方式排列. 在每個格點上有一個處理器,所有處理器中都含有同樣多的狀態,每個元胞都處于一系列有限狀態中的某種狀態. 時間被離散成均勻的時刻,稱為時鐘. 當時鐘滴答一下時,所有元胞的狀態都發生改變. 元胞自動機可用于模擬許多復雜系統,特別是處于自組織臨界狀態的系統,例如植被的演化[7]、 生態演化[8]和交通流動[9]等.

本文考慮二維面上的一層氣泡. 將氣泡所在空間用正六角形蜂房結構代替,如圖1所示,給出二維空間的蜂房剖分,每個正六角形的內切圓是一個氣泡. 每個氣泡的中心將組成與蜂房的對偶網格Di,j,每點(i,j)存在不同的水重級別,稱為該點的狀態值. 氣泡破裂時的狀態值稱為臨界狀態值,其大于各級別的狀態值. 當狀態值為零時表示氣泡已破裂狀態. 在下一時刻,由于水重的增加使得狀態值增加,超過時氣泡發生破裂,并將水重均分給周圍可能存在的氣泡,從而構成一個多狀態的元胞自動機.

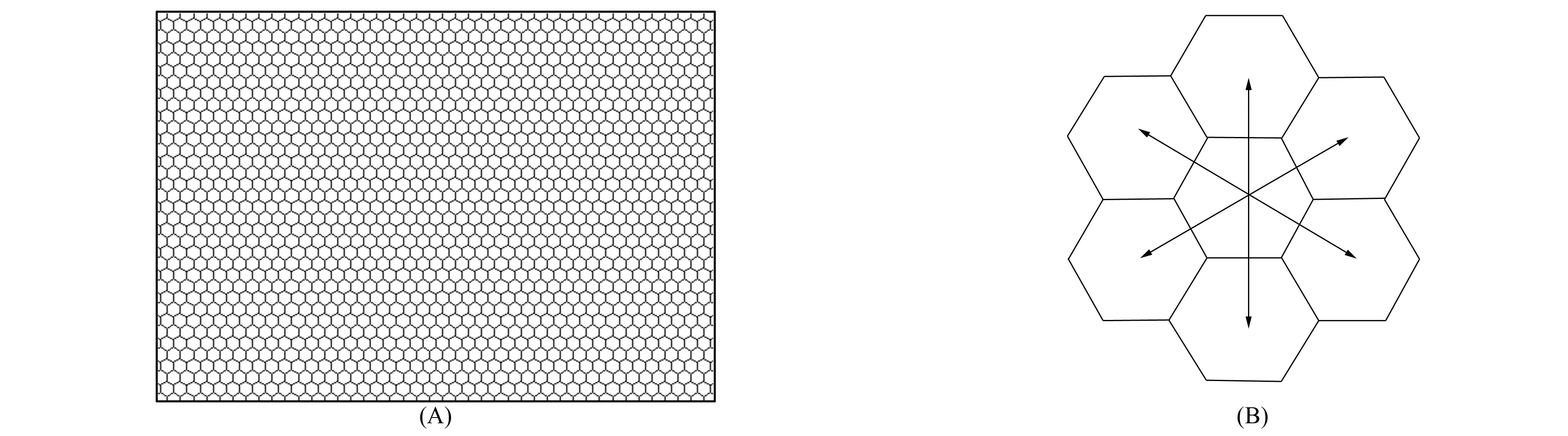
圖1 蜂房網格(A)和單胞及其對偶網格(B)Fig.1 Honeycomb grid (A) and unit cell and its dual grid (B)

1.1 非飽和狀態 非飽和狀態是指某點周圍當前時刻沒有破裂氣泡,則此時元胞自動機的鄰居數為6. 本文選擇6行5列的蜂房,如圖2所示. 取氣泡的臨界狀態值為11,以3行3列位置上的氣泡為起始點,當起始點的狀態數增加2時,某個氣泡的狀態數達到11發生破裂,狀態值立刻變為0. 然后將其狀態值等分添加到周圍,如圖3所示.

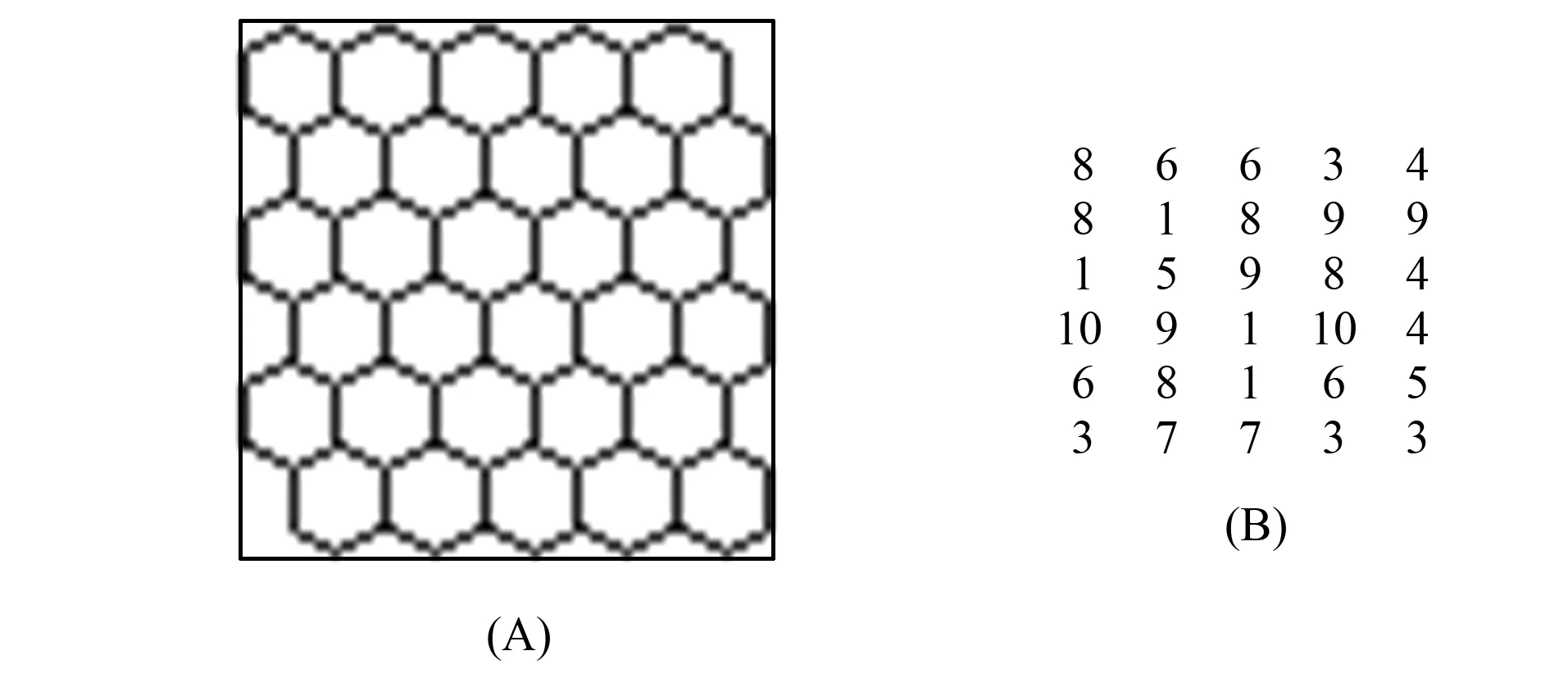
圖2 6×5蜂房及級別點陣Fig.2 Honeycomb lattice 6 rows×5 columns and level

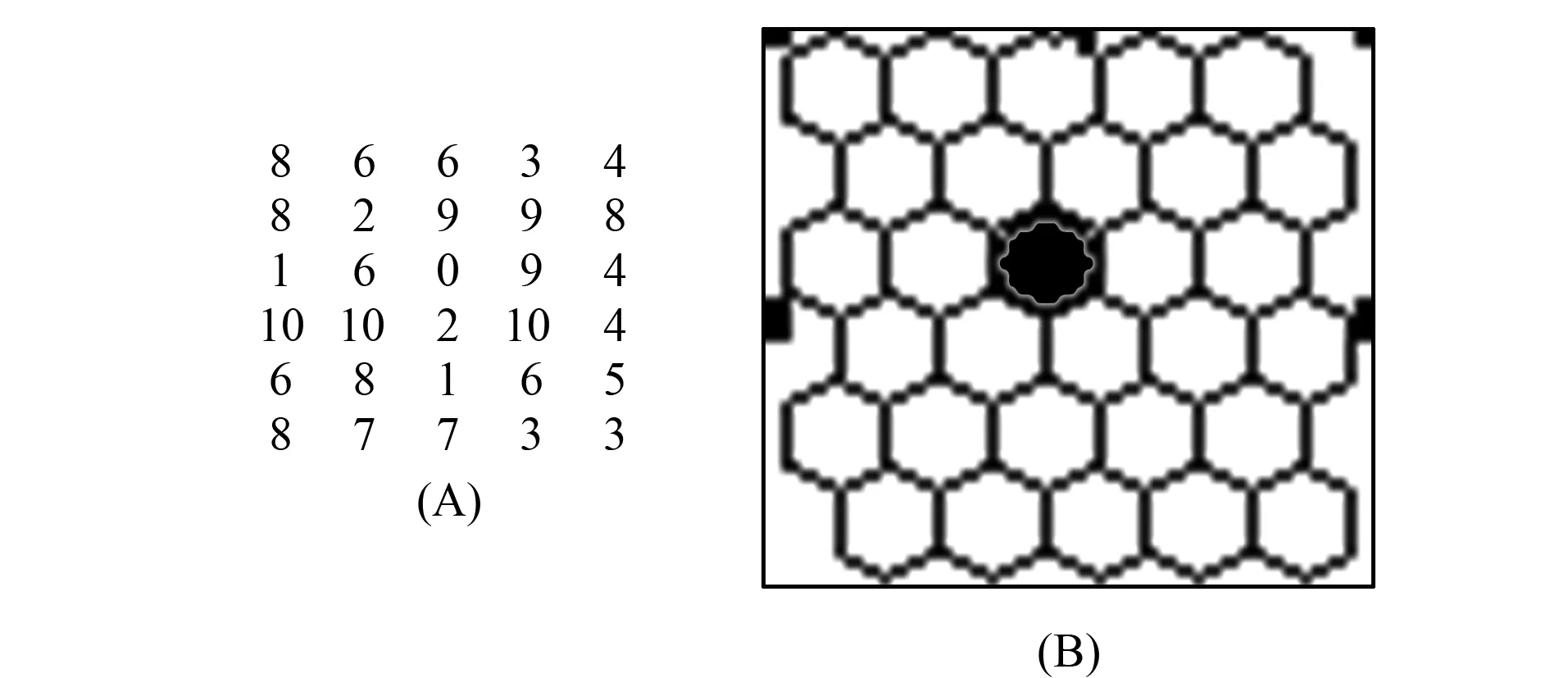
圖3 下一時刻狀態(A)和破裂氣泡(B)(實心圓表示破裂的氣泡)Fig.3 State (A) and burst bubbles (B) in the next moment (including solid circle said burst bubbles)

1.2 飽和狀態 當某氣泡的周圍存在破裂氣泡時,稱該點處于飽和狀態. 此時需要確定非破裂氣泡數量. 例如,當周圍有一個破裂氣泡時,則需要將狀態5均分.

1.3 氣泡塌陷 氣泡塌陷是指當超過臨界狀態時,氣泡沒有破裂而容易破裂,即它的臨界狀態值變小. 由于本文考慮的氣泡是均勻且體積不變的,因此,從體積上看不出該過程,可以理解成氣泡變薄,不能承受原來(上一步)時的水重,破裂狀態的臨界值變小. 一種極端的情況是沒有塌陷過程,當前狀態超過臨界狀態值時,氣泡破裂,狀態值變為零. 本文采用氣泡無塌陷破裂進行模擬.

2 大規模氣泡湮滅模擬

2.1 42×50氣泡群 在二維平面上均勻分布42×50個氣泡. 初始時刻,隨機給出氣泡狀態. 圖4為初始時刻氣泡群的狀態點陣,臨界狀態值為16.

圖4 初始時刻氣泡群的狀態點陣Fig.4 State of bubble group in the initial moment

選擇(i,j)=(20,24)為啟動點,即在該點是增加水重的氣泡,在模擬過程中,該點始終在增加狀態值. 當該點加入的狀態值為12時,有1個氣泡破裂,如圖5所示. 當輸入狀態值為56時,氣泡破裂10個,如圖6所示. 當輸入狀態值為62時,氣泡破裂的圖形形狀有改變,但是破裂數目仍為10個,如圖7所示. 繼續加大輸入狀態值,當輸入狀態值增加到86時,氣泡破裂17個. 破裂情況如圖8所示.

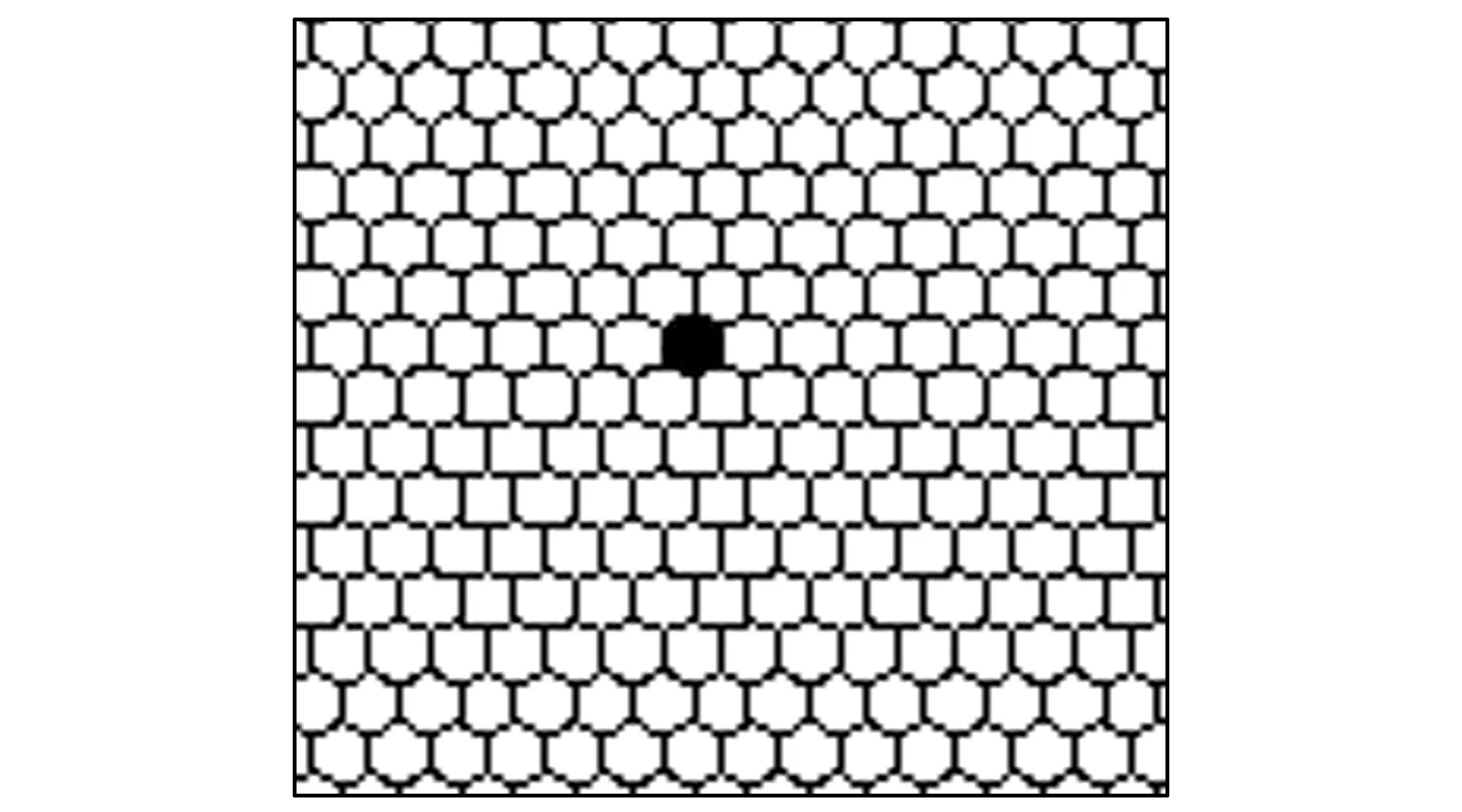
圖5 氣泡在(i,j)=(20,24)處破裂快照Fig.5 Snapshot of the bubbles burst at location(i,j)=(20,24)

圖6 輸入狀態值為56時氣泡破裂快照Fig.6 Snapshot of bubble burst at input status value to 56

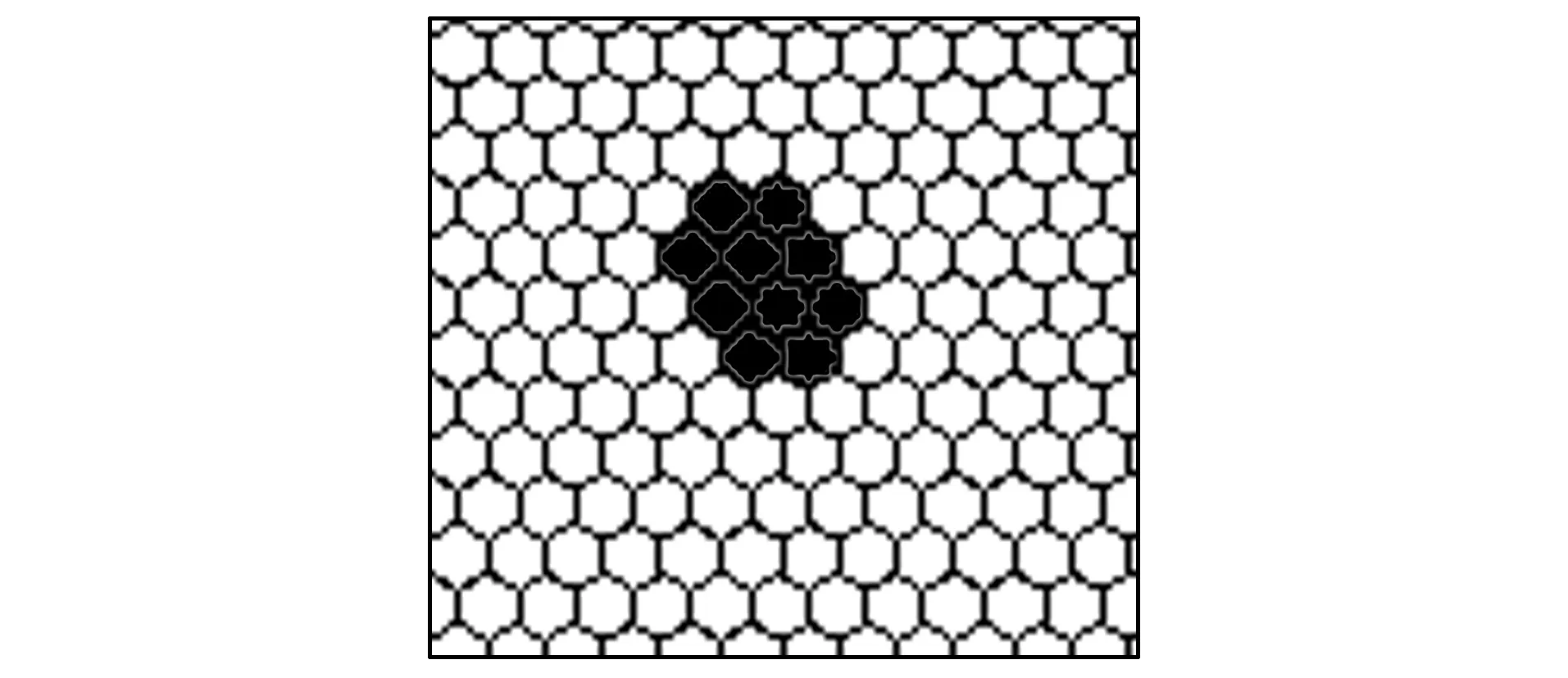
圖7 輸入狀態值為62時氣泡破裂快照Fig.7 Snapshot of bubble burst at input status value to 62

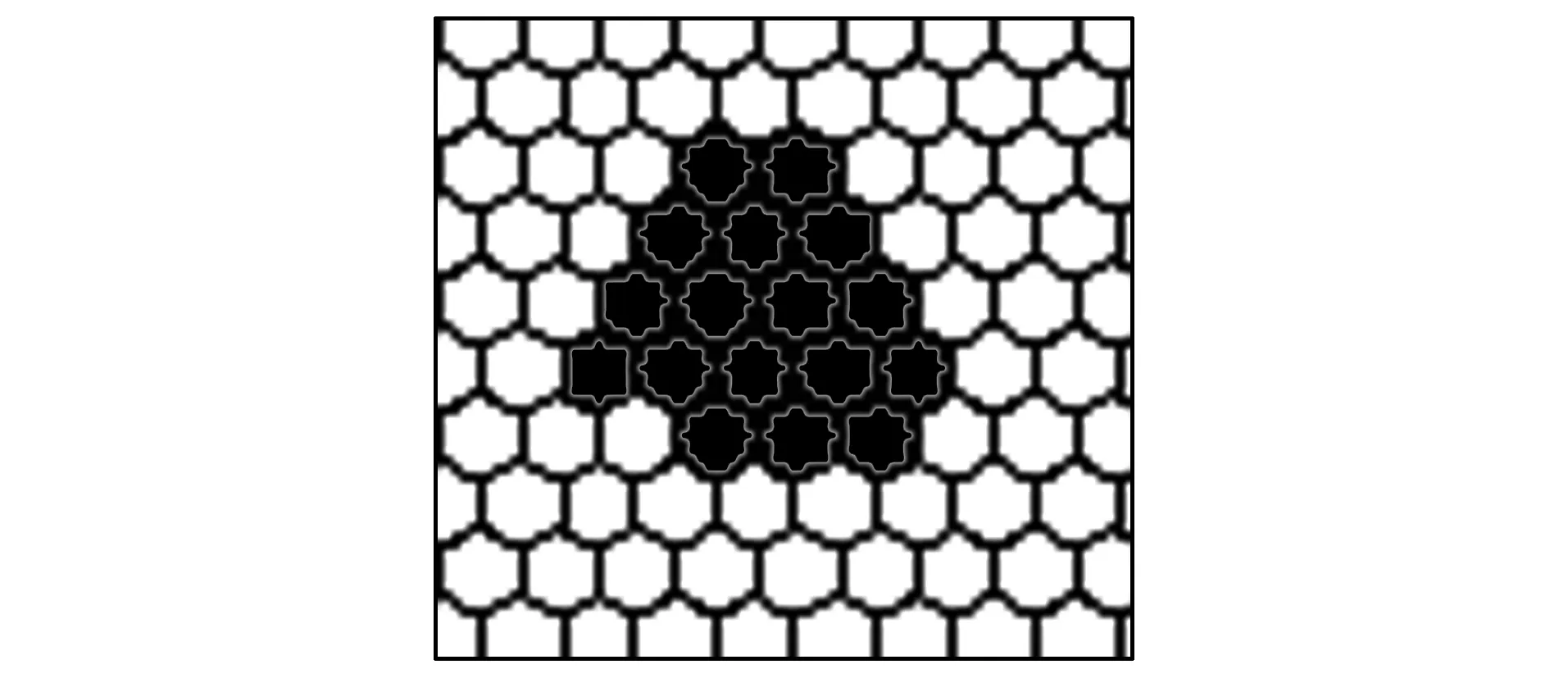
圖8 輸入狀態值為86時氣泡破裂快照Fig.8 Snapshot of bubble burst at input status value to 86

繼續增加輸入狀態值,當輸入狀態值超過133時,氣泡破裂的范圍不再發生變化,此時整個結構已處于自組織臨界狀態,當輸入狀態值增加1時,所有氣泡全部破裂,出現氣泡群的湮滅現象. 圖9給出了氣泡破裂個數與輸入狀態值間的關系,由于在演化過程中,每一步增加一個狀態值,因此該狀態數實際上相當于時間步.

2.2 292×232氣泡群 模擬292×232個氣泡群的破裂情況,圖10給出了氣泡破裂個數與輸入狀態值間的關系. 模擬結果表明,該系統氣泡破裂的個數只有如下6種情況: 4,5,7,19,21,83,稱為系統的狀態級,記K=1,2,…,6. 為了考察可能出現的Zipf定律,將上述狀態級轉化成Richter級:L=7-K,并給出它們之間的對數關系,如圖11所示,可得一個大規模氣泡湮滅的Zipf律: log(N)=Alog(L)+C,其中:A=-1.69 4;C=1.92. 結果表明,大規模氣泡湮滅是自組織臨界的.

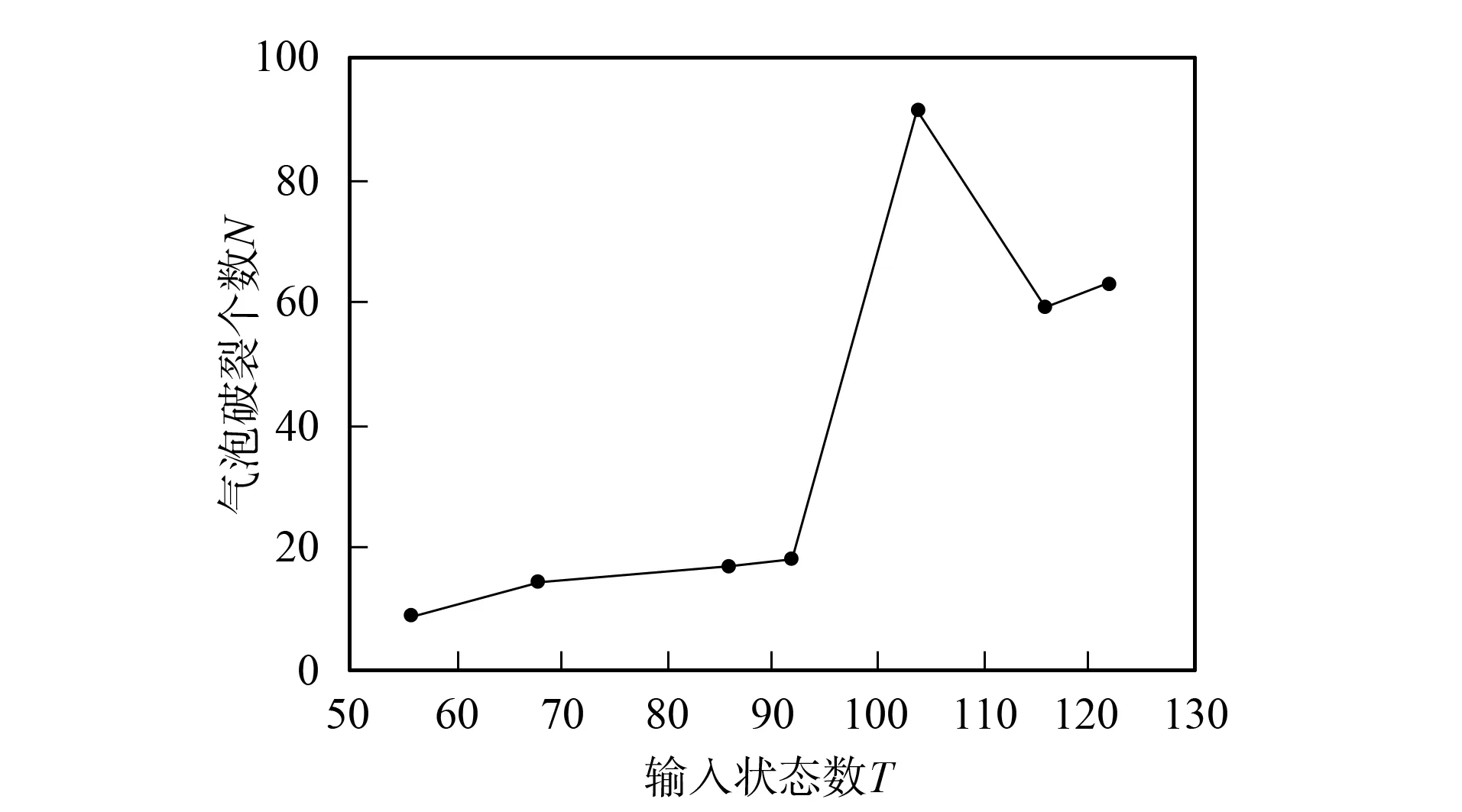
圖9 42×50氣泡群氣泡破裂個數與輸入狀態值間的關系Fig.9 Relationship between the 42×50 input state value and the number of bubbles burst

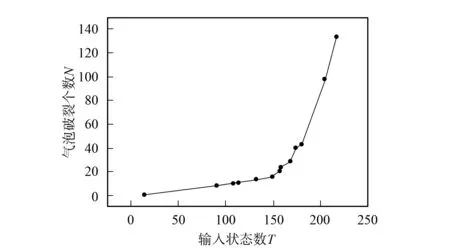
圖10 292×232氣泡群氣泡破裂個數與輸入狀態值間的關系Fig.10 Relationship between the 292×232 input state value and the number of bubbles burst

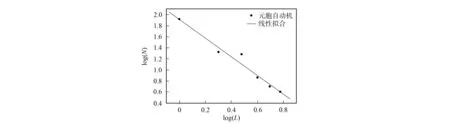
圖11 氣泡群Richter級L與相應氣泡破裂數N間的對數關系Fig.11 Corresponding logarithmic relationship between bubble burst number N and magnitude on the Richter scale L

綜上可見,本文模型采用了最簡單假設,僅給出了大規模氣泡的湮滅現象. 真實的氣泡是三維的、 大小不均勻分布的,并且具有塌陷過程. 模擬真實氣泡湮滅過程需要結合實驗,反復矯正模型的狀態級別和臨界值,同時要考慮三維非均勻分布.

[1]Bak P,TANG Chao,Wiesenfeld K,Self-organized Criticality: An Explanation of 1/fNoise [J]. Phys Rev Lett,1987,59: 381-384.

[2]Bak P,TANG Chao,Wiesenfeld K. Self-organized Criticality [J]. Phys Rev A,1988,38(3): 364-374.

[3]Bak P. How Nature Works: The Science of Self-organized Criticality [M]. New York: Springer-Verlag,1996.

[4]Seck-Tohu-Mora J C,Medina-Marino J,Martínez G J,et al. Emergence of Density Dynamics by Surface Interpolation in Elementary Cellular Automata [J]. Communications in Nonlinear Science and Numerical Simulation,2014,19(4): 941-966.

[5]Yan G W,Zhang J Y,Wang H M,et al. Simple Stochastic Lattice Gas Automaton Model for Formation of River Networks [J]. Phys Rev E,2008,78(6): 066102.

[6]閆廣武. 元胞自動機與人工生命研究進展 [J]. 吉林大學學報: 理學版,2003,41(1): 40-44. (YAN Guangwu. Advances of the Studies on the Cellular Automata and Artificial Life [J]. Journal of Jilin University: Science Edition,2003,41(1): 40-44.)

[7]Ye F,Chen Q W,Li R N. Modelling the Riparian Vegetation Evolution Due to Flow Regulation of Lijiang River by Unstructured Cellular Automata [J]. Ecological Informatics,2010,5: 108-114.

[8]Ferreri L,Venturino E. Cellular Automata for Contact Ecoepidemic Processes in Predator-Prey Systems [J]. Ecological Complexity,2013,13: 8-20.

[9]XUN Jing,NING Bin,LI Keping,et al. The Impact of End-to-End Communication Delay on Railway Traffic Flow Using Cellular Automata Model [J]. Transportation Research Part C: Emerging Technologies,2013,35: 127-140.

(責任編輯： 趙立芹)

CellularAutomataSimulationforBubblesAnnihilationinaLargeNumbers

HU Yajun,YAN Guangwu
(CollegeofMathematics,JilinUniversity,Changchun130012,China)

With the help of a proposed cellular automata model for the two-dimensional bubble annihilation and a honeycomb structure instead of the two-dimensional bubbles,we simulated the process of the bubble collapse at a load beyond the critical load. This result shows the process meets Zipf’s law.

cellular automata; two-dimensional bubble; Zipf’s law

2014-02-25.

胡亞軍(1990—),男,漢族,碩士研究生,從事流體力學與復雜系統的研究,E-mail： h76101@gmail.com. 通信作者: 閆廣武(1964—),男,漢族,博士,教授,博士生導師,從事流體力學與復雜系統的研究,E-mail: yangw_jlu@126.com.

國家自然科學基金(批準號: 11272133).

O231.5

A

1671-5489(2014)05-0975-04