形函數時變性對汽車公路梁橋豎向耦合振動影響分析

陳代海，陳 淮，李 整，郭文華

(1.鄭州大學 土木工程學院，鄭州 450001；2.中南大學 土木工程學院，長沙 410075)

用有限元法分析汽車與梁橋耦合振動時，梁單元內部插值一般用三次Hermite形函數N[1]，若用x表示車輪與梁單元接觸點在該單元內的相對位置，因梁單元的形函數為x的函數，則N可表示為N=N(x)。汽車在橋梁上行駛時，x為行車速度v與時間t的函數[2]，即x=x(v,t)，此時N不僅為距離x的函數，亦為時間t的函數，即N=N(x,t)。此由時間變化引起的形函數特性定義為梁單元形函數時變性。公路橋梁車輛耦合振動分析中通常不考慮形函數時變性對車橋耦合系統豎向振動響應影響。用大型通用有限元軟件計算時(該類軟件目前無法考慮形函數時變性)，關于形函數時變性對車橋豎向振動響應影響及所需考慮其影響情況均值得探討。

國內外對鐵路橋與列車的車橋耦合振動研究較多[3-6]，探討不同因素對車橋耦合振動影響[7-9]。但對公路橋梁與汽車的車橋耦合振動研究較少。韓萬水等[10]對實測路面粗糙度下車橋系統動力響應及頻譜特性進行對比分析；殷新鋒等[11]研究輪胎接觸面對車橋耦合振動影響；王達等[12]計算3種不同橋面平整度下大跨度懸索橋車橋耦合振動響應。現有車橋耦合振動研究中，往往忽略梁單元形函數時變性對車橋動力響應影響。

本文據車橋耦合振動分析理論，引入Hermite插值函數，推導形函數時變性在車橋耦合振動方程中的貢獻值。以公路簡支T梁橋為例，汽車采用多剛體振動模型，計算汽車以不同車速通過簡支T梁橋時的車橋豎向動力響應，探討梁單元形函數時變性對汽車公路梁橋豎向耦合振動影響。

1 車橋耦合振動方程

以橋梁在自重、無車輛作用下的平衡狀態為初始狀態，分別以橋梁與車輛靜平衡位置為坐標原點建立坐標系，見圖1。由于橋梁多采用彈性連續體模擬，故可用常規有限元法首先獲得橋梁自身質量矩陣Mb、剛度矩陣Kb及阻尼矩陣Cb；而汽車多采用彈簧、阻尼相連的多剛體模型，易于單獨計算作用在橋梁上的車輛慣性力、阻尼力、彈性力及虛功，其動力特性矩陣由“對號入座”法則[3]形成。

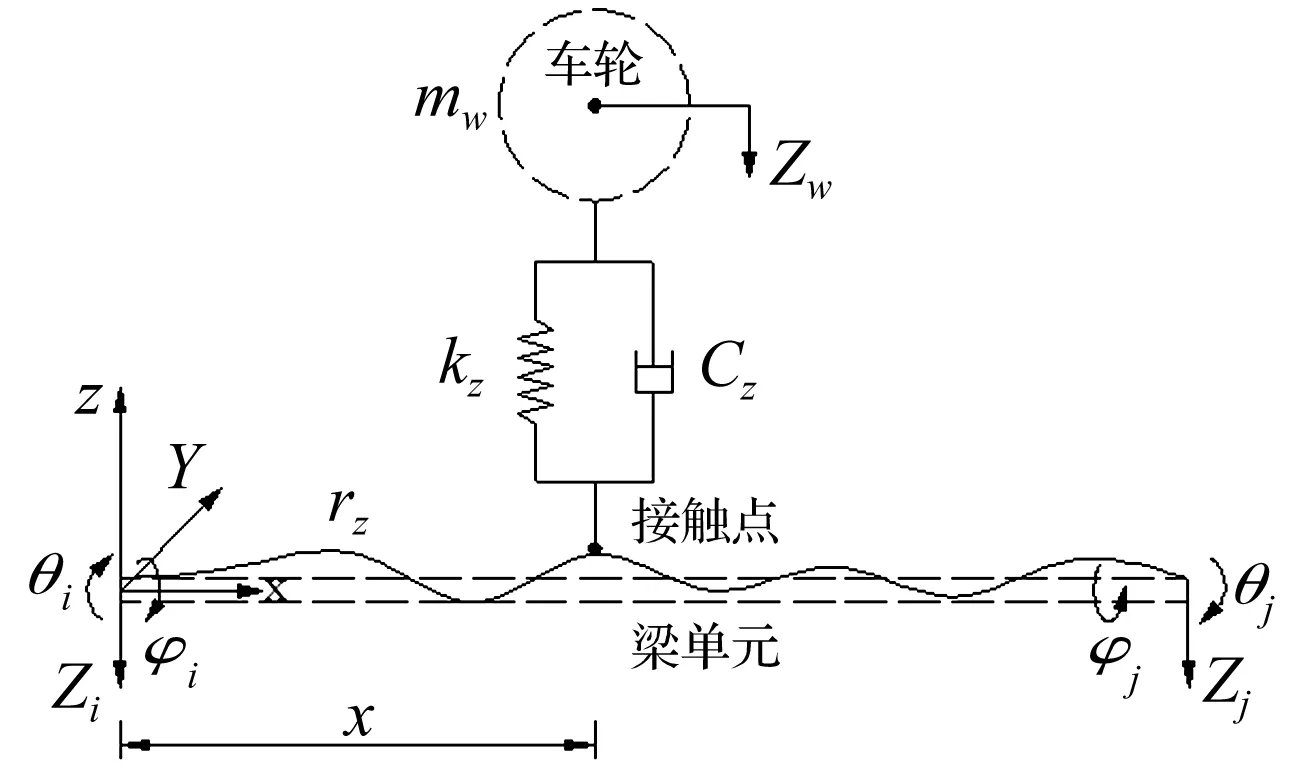
圖1 車橋接觸點示意圖

對汽車的多剛體模型，阻尼元件可分為兩類，第一類連接兩剛體，兩端產生的相對速度僅與車輛自由度有關；第二類一端連接剛體，一端位于接觸點，兩端產生的相對速度不僅與車輛自由度有關，亦與橋梁自由度、路面粗糙度有關。計算第一類阻尼元件阻尼力所作虛功，提取相應阻尼系數，直接形成汽車阻尼子矩陣Cv。計算第二類阻尼元件阻尼力所作虛功，提取相應阻尼系數，直接形成附加的汽車阻尼子矩陣Cv1、車橋耦合阻尼矩陣Cbv，Cvb及附加的橋梁阻尼子矩陣Cbbv；提取相應荷載系數，可直接形成對橋梁的附加荷載列陣Pbvr2及對汽車的附加荷載列陣Pvr2。相應剛度矩陣可用形成阻尼矩陣方法獲得。汽車軸重作為外荷載形成對橋梁的附加荷載列陣Pbvg。詳見文獻[13]。

將汽車與橋梁視為整體系統，據全計算化原理[14]，將單獨橋梁振動方程直接擴充為橋梁-汽車耦合系統振動方程：

(1)

汽車行駛在橋梁上時，橋梁-汽車耦合系統運動方程為一組變系數的二階微分方程。需注意的是，隨汽車位置的變化，并非所有子矩陣均隨時間變化，如Mb，Mv，Kb，Kv，Kv1，Cb，Cv，Cv1，Pbvg。編制計算程序時，該子矩陣可專門儲存以便隨時調用。而有些子矩陣如Mbbv，Kbbv，Kbv，Kvb，Cbbv，Cbv，Cvb，Pbrv1，Pbrv2，Prv1，Prv2均為時變的，需據每步不同車輛運行位置重新形成，并疊加到相應位置。因各總體矩陣隨時間變化，故此車橋系統亦稱時變系統。

采用直接積分法求解式(1)(車輛與橋梁視為整體系統，無需迭代求解)，可同時獲得橋梁與汽車的空間動力響應。據上述原理，用Fortran語言編制橋梁-汽車耦合系統動力分析軟件BVIP (Bridge Vehicle Interaction Program)。該軟件功能較完善，不限定具體橋梁形式，可用于由梁單元、桿單元、質量點單元等模擬的常見橋梁，如簡支梁、連續梁、連續剛構橋、斜拉橋等；亦可考慮不同車輛類型、任意車輛數目、多車道及車輛相向行駛等多種工況[13]。

2 形函數時變性在車橋耦合振動方程中的體現

形函數時變性在車橋耦合振動方程中的體現主要通過慣性力、阻尼力對系統阻尼矩陣、剛度矩陣進行修正實現。以阻尼力修正剛度矩陣為例進行說明。選某第二類豎向阻尼元件(一端連接剛體，一端位于接觸點處，見圖1)，在是否考慮梁單元形函數時變性兩種情況下，計算阻尼力所做虛功，比較二者差異，從而體現形函數時變性對車橋耦合振動方程影響。

汽車通過橋梁時，設車輪與路面始終保持接觸，車輪與橋梁接觸點位移zjcd包含橋梁動態位移zb與路面粗糙度rz兩部分，即

zjcd=zb+rz

(2)

式中：zb為橋梁動態位移，可表示為

zb=ND

(3)

式中：

N=[N1N5dyN2N3N6dyN4]

(4)

(5)

D=[ziφiθizjφjθj]T

(6)

式中：zi，φi，θi，zj，φj，θj分別為梁單元i，j端豎向位移、繞X軸轉角、繞Y軸轉角；dy為接觸點與橋梁單元形心在整體坐標系中y坐標差；l為單元長度。

(7)

(8)

阻尼力所做虛功δWc可表示為

(9)

不考慮梁單元形函數時變性時，即N=N(x)，則

(10)

此時阻尼元件兩端豎向相對速度為

(11)

阻尼力所做虛功為

N2δθi-N3δzj-N6δφjdy-N4δθj)

(12)

式中：v=?x/?t為行車速度，僅考慮勻速行車情況，即v為常量。

考慮梁單元形函數時變性時，即N=N(x,t)，則

(13)

式中：

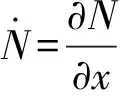
(14)

此時阻尼元件兩端豎向相對速度為

(15)

阻尼力所做虛功為

N2δθi-N3δzj-N6δφjdy-N4δθj)

(16)

3 算例分析

3.1 橋梁模型

為簡化計算，以公路簡支T梁橋為研究對象，橋長50 m，T梁高1.74 m，翼緣板寬2.4 m、厚0.24 m，腹板厚0.2 m。采用空間梁單元離散橋梁結構，按簡支梁支座布置形式設置橋梁邊界條件。對常見的多片式公路橋建立有限元模型時，為考慮橫隔板影響，可用梁單元模擬橫隔板，將多片式公路橋離散成由梁單元組成的梁格體系。

3.2 汽車模型

圖2 汽車模型圖

汽車采用由彈簧、阻尼器相連的多剛體模型，彈簧均為線性，阻尼按粘性阻尼計算，車輪與橋面豎向密貼，將隨機橋面粗糙度作為激勵輸入。車身具有側擺、浮沉、側滾、點頭、搖頭5個自由度，4個車輪分別具有側擺、浮沉2個自由度，每輛汽車共有13個自由度，見圖2。模型各參數取值見文獻[13]。

3.3 路面粗糙度模型

選定功率譜密度函數后，采用三角級數法產生路面粗糙度樣本值[13]：

(17)

式中：r(x)為產生的路面粗糙度序列；S(Ωk)為給定功率譜密度函數；Ωk為在給定譜密度間隔內第k個空間頻率(k=1,2,…,N)，其中Ω1，ΩN分別為考慮頻率的下限、上限；ΔΩ為頻率間隔帶寬；θk為[0～2π]內均勻分布幅角。

3.4 形函數時變性對車橋耦合振動影響分析

基于橋梁、汽車有限元模型，計入路面粗糙度，采用自編分析程序，在是否考慮梁單元形函數時變性情況下，分別計算汽車以不同車速通過橋梁時車橋動力響應。選廂式貨車、一汽佳寶及桑塔納三種典型汽車分析參數[15]，10輛車組成一個車隊，每輛車類型由計算機生成的隨機數隨機確定，見圖3。計算時，車速分別取60 km/h、80 km/h、100 km/h、120 km/h。

圖3 車隊車輛類型布置示意圖

橋梁上選跨中位置、車輛中選車隊第1輛汽車分別給出相應豎向振動響應。不同車速下車橋豎向動力響應幅值比較見表1、圖4、圖5，橋梁中點及車體重心時程響應曲線見圖6～圖8，其中，“考慮”、“不考慮”分別表示是否考慮梁單元形函數時變性情況。

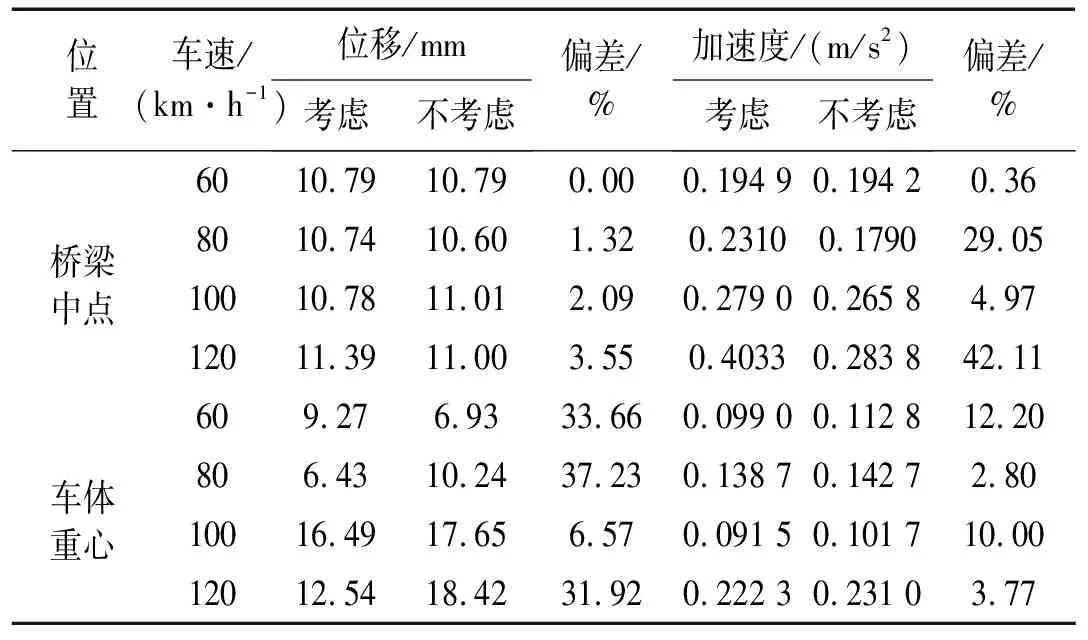
表1 形函數時變性考慮前后車橋豎向動力響應幅值比較

圖4 橋梁中點豎向加速度幅值比較

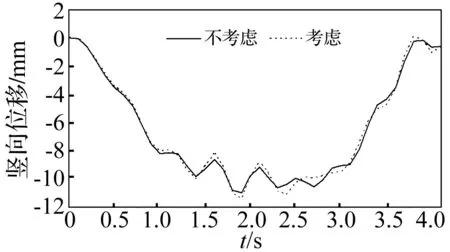
圖7 車速120 km/h時橋梁中點豎向位移時程比較

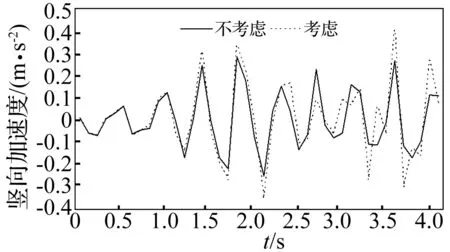
圖8 車速120 km/h下橋梁中點豎向加速度時程比較

由表1、圖4、圖5看出，梁單元形函數時變性對車橋豎向動力響應幅值存在影響。對橋梁響應而言，該影響有隨車速增加而增大趨勢，此因考慮形函數時變性后，慣性力及阻尼力增加與速度相關的附加項，增加速度可加大對車橋耦合系統影響。對車體響應，較形函數時變性對加速度幅值影響，其對位移幅值影響明顯，該點對橋梁響應恰恰相反。

對比圖6、圖7發現，速度增大情況下梁單元形函數時變性對橋梁中點豎向位移影響愈加顯著。由圖7、圖8看出，當汽車以高速通過橋梁時，形函數時變性對車橋耦合系統影響明顯。

4 結 論

(1) 考慮梁單元形函數時變性后，慣性力、阻尼力表達式中增加與速度相關的附加項，其對車橋耦合系統剛度矩陣、阻尼矩陣進行修正，速度增加加大其對車橋耦合系統豎向振動影響。

(2) 車橋豎向振動分析中，尤其高速行駛車輛車橋耦合振動分析中，需考慮梁單元形函數時變性影響。

[1] 余華, 吳定俊.Hermite插值在車橋耦合振動中的應用[J].振動與沖擊, 2006, 25(2): 38-40.

YU Hua, WU Ding-jun.Application of Hemite function in vehicle-bridge interaction analysis[J].Journal of Vibration and Shock, 2006, 25(2):38-40.

[2] 李東平, 孫旭光, 周智輝, 等.梁單元形函數在車橋時變系統振動分析中的選取研究[J].鐵道科學與工程學報, 2010, 7(6): 12-17.

LI Dong-ping, SUN Xu-guang, ZHOU Zhi-hui, et al.Research on election of beam element interpolation function in coupling vibration analysis of variational coefficient vehicle-bridge system[J].Journal of Railway Science and Engineering, 2010, 7(6):12-17.

[3] 曾慶元, 郭向榮.列車橋梁時變系統振動分析理論與應用[M].北京：中國鐵道出版社，1999.

[4] 夏禾, 張楠.車輛與結構動力相互作用[M].北京：科學出版社，2002.

[5] Bruno D, Greco F, Lonetti P.Dynamic impact analysis of long span cable-stayed bridges under moving loads[J].Engineering Structures, 2008, 30(4):1160-1177.

[6] Yau J D, Yang Y B.Vibration reduction for cable-stayed bridges traveled by high-speed trains[J].Finite Elements in Analysis and Design, 2002, 40(3):341-359.

[7] 李永樂, 吳夢雪, 臧瑜, 等.大跨度懸索橋梁端豎向折角對列車走行性的影響研究[J].土木工程學報, 2012, 45(8): 114-120.

LI Yong-le, WU Meng-xue, ZANG Yu, et al.Effects of vertical rotation angle at girder ends on train running performance for large-span suspension bridges[J].China Civil Engineering Journal, 2012, 45(8): 114-120.

[8] 李小珍, 喻璐, 強士中.不同主梁豎曲線下大跨度斜拉橋的車橋耦合振動分析[J].振動與沖擊, 2003, 22(2): 43-46.

LI Xiao-zhen, YU Lu, QIANG Shi-zhong.Vehicle-bridge interaction of long-span cable-stayed bridges with various vertical girder curves[J].Journal of Vibration and Shock, 2003, 22(2): 43-46.

[9] 吳定俊, 李奇, 高丕勤.軌道不平順速度項對車橋動力響應的影響分析[J].同濟大學學報(自然科學版), 2006, 34(4): 494-498.

WU Ding-jun, LI Qi, GAO Pi-qin.Dynamic response of vehicle-bridge system due to track irregularity coupling with velocity of the vehicle[J].Journal of Tongji University (Natural Science), 2006, 34(4): 494-498.

[10] 韓萬水, 馬麟, 院素靜, 等.路面粗糙度非一致激勵對車橋耦合振動系統響應影響分析[J].土木工程學報, 2011, 44(10): 81-90.

HAN Wan-shui, MA Lin,YUAN Su-jing, et al.Analysis of the effect of inconsistent stimulus of surface roughness on vehicle-bridge coupling vibrations[J].China Civil Engineering Journal, 2011, 44(10): 81-90.

[11] 殷新鋒, 劉揚, 蔡春生, 等.輪胎接觸面對車-簡支梁橋耦合振動的影響[J].長沙理工大學學報(自然科學版), 2012, 9(1):41-45.

YIN Xin-feng, LIU Yang, CAI Chun-sheng, et al.Vehicle-simple supported beam bridge coupled vibration based on the patchcontact[J].Journal of Changsha University of Science and Technology (Natural Science), 2012, 9(1):41-45.

[12] 王達, 韓萬水, 黃平明, 等, 橋面平整度對大跨度懸索橋車橋耦合振動的影響[J] 長安大學學報(自然科學版), 2009, 29(4): 53-58.

WANG Da, HAN Wan-shui, HUANG Ping-ming, et al.Influence of bridge surface roughness on vehicle-bridge coupled vibration of long-span suspension bridge[J].Journal of Chang’an University (Natural Science Edition), 2009,29(4): 53-58.

[13] 陳代海.地震作用下車橋耦合系統動力響應及振動控制研究[D].長沙: 中南大學, 2011.

[14] Guo Wen-hua.Dynamic analysis of coupled road vehicle and long span cable-stayed bridge systems under cross winds[D].Hong Kong: The Hong Kong Polytechnic University, 2003.

[15] 韓萬水.風-汽車-橋梁系統空間耦合振動研究[D].上海: 同濟大學, 2007.