諧波激勵下多尺度粘滑干摩擦系統混沌

閻 俊，徐 超

(西北工業大學 航天學院，西安 710072)

工程結構多由螺栓、鉚釘等連接裝配。振動環境下連接結合面在法向可能出現間隙、分離及碰撞，在切向可能出現摩擦、滑移及滑動等非線性現象，導致連接結構發生復雜的動力學行為。對含結合面摩擦系統的研究一直為非線性動力學領域研究重點。何阿平等[1]對摩擦學行為的混沌特性進行定量研究，并實驗證明摩擦學系統混沌特性。吳文健等[2]分析由干摩擦引起的粘滑振動及系統穩定性，采用數值方法獲得系統經周期運動失去穩定性通用混沌路徑。韓彥等[3]對干摩擦振動系統響應計算方法進行述評。陳建縣[4]分別從摩擦特性、摩擦力模型、摩擦系統自激振動、強迫振動及摩擦振動控制等系統綜述機械系統滑動干摩擦動力學近期研究進展，指出含摩擦系統動力學研究對工程設計、優化及控制的重要意義。

結合面干摩擦描述形式對建模系統非線性動力學特性有重要影響[5]。文獻[6]對機械系統中摩擦模型進行評述，系統介紹多種常用摩擦模型，并對每種模型的構成、特點及適用范圍進行較詳細論述，認為動態摩擦模型能更好描述摩擦非線性行為。文獻[7]對采用不同動態摩擦模型的系統非線性動力學行為進行研究，指出不同摩擦力模型的優點與不足。對一般機械結合面而言，接觸壓力分布不均勻，在切向振蕩載荷作用下，結合面將反復經歷從微觀尺度滑移到宏觀尺度滑動的多尺度動態摩擦過程。機械摩擦動力學研究中廣泛采用的庫倫摩擦模型雖形式簡單，卻不能準確描述多尺度物理過程[4,6]。文獻[8]從結合面摩擦物理機理入手，在遲滯非線性模型[9]基礎上導出描述連接面多尺度粘滑摩擦過程的參數化模型形式。文獻[10]通過引入并聯線性剛度項及均勻分布臨界滑移力分布密度函數形式，給出改進的描述結合面多尺度粘滑過程的力學模型。

本文以典型含連接結合面振動系統為研究對象，采用滑動位移的遲滯模型[10]描述結合面多尺度粘滑摩擦過程，利用中心差分法，數值研究系統受諧波強迫激勵時在主共振、次共振條件下的混沌特性。

1 含結合面多尺度粘滑摩擦系統模型

機械結構中典型的螺栓連接見圖1。兩被連接件通過施加預緊載荷螺栓裝配在一起。通常預緊力在結合面上產生的接觸壓力p分布并非均勻，靠近螺栓孔中心區域的接觸壓力高，離中心越遠接觸壓力越低。

圖1 切向力作用螺栓連接結構

受切向載荷作用時，接觸壓力較低區域先發生滑動，而接觸壓力較高區域仍保持粘滯，從而接觸界面處于既存在局部滑移亦存在局部粘滯狀態；若切向載荷足夠大，則整個結合面處處均會發生滑動，即形成動態相對運動。局部滑移可能發生于10-6～10-4m尺度，而宏觀滑動則可能發生在10-3～10-2m尺度；因此，結合面動態摩擦過程具有典型的多尺度特征。

考慮圖1諧波激勵下典型的螺栓連接系統，因對稱性且只考慮沿結合面的切向運動，可簡化為圖2(a)的運動模型。模型中下連件固定，上連件考慮為一維運動剛體。u，f，fesin(ωt)分別為結合面相對位移、非線性遲滯恢復力及諧波外激勵力。連接系統剛度包括并聯兩部分，即由結合面粘滑摩擦行為的貢獻及因連接件柔性的貢獻。前者隨結合面相對位移增大而減小呈非線性變化，后者視作線性剛度。令k表示系統初始總剛度，與結合面粘滑摩擦行為無關的線性剛度為ka=k，無量綱系數0<α<1；則描述結合面粘滑摩擦部分的子系統初始剛度為k-ka。

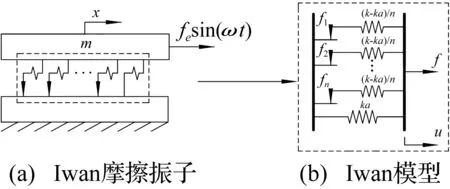
圖2 Iwan摩擦振子及Iwan模型

力學模型實際為并聯的線性剛度項Iwan模型[10]，見圖2(b)，其采用n個彈簧滑塊單元并聯組成的子系統(經典Iwan模型)描述結合面多尺度粘滑摩擦行為。子系統中每個線性彈簧剛度ki(i=1,2,…n)均為(k-ka)/n，但每個滑塊的臨界滑移力fi(i=1,2,…n)不相同。系統切向受載時，臨界滑移力小的滑塊先發生滑動，隨相對位移增大，發生滑移滑塊越多，直至全部滑移，即結合面出現宏觀相對運動；因此，該模型可較好復現結合面上復雜的多尺度粘滑摩擦過程。

考慮經典Iwan模型連續形式，取n→∞，則fi需定義成分布密度函數Φ(fi)形式(表達式非唯一)。定義Φ(fi)為均勻分布形式[11]，即

(1)

式中：fy為結合面恰發生宏觀滑移時對應的臨界宏觀滑移力。

經典Iwan模型恢復力骨干(backbone)曲線fo可表示為未發生滑移的彈簧滑塊單元與發生滑移的彈簧滑塊單元上恢復力之和,即

(2)

將式(1)代入式(2)積分并整理得：

fo[k(1-α),u]=

(3)

式(3)分段函數包括兩部分，分別表示結合面處于局部滑移與宏觀滑動狀態時恢復力-變形關系。振蕩載荷下結合面會出現反復的卸載-加載運動。據梅辛準則[8],得遲滯過程中Iwan模型恢復力函數為

(4)

式中：fl，fu分別為卸載、加載中恢復力；A為系統一個振動周期內最大振幅。

引入無量綱參數g=f/fy,q=ku/fy,Q=kA/fy對式(2)、(4)正則化得：

(5)

(6)

據牛頓第二運動定律，圖2(a)系統運動方程可表示為

(7)

對式(7)正則化，兩邊同乘k/(mfy)得：

(8)

(9)

2 計算方法

式(9)振動系統遲滯恢復力具有變剛度、變阻尼非光滑、強非線性特點，公式解析解較難獲得。本文用中心差分法求解運動方程，研究多尺度粘滑摩擦系統隨外激勵幅值逐漸增大表現出的分岔及混沌特征。

由于恢復力分段及遲滯特性，數值仿真中準確判斷轉折點至關重要。

2.1 局部滑移與宏觀滑移轉折點

由式(5)知，該轉折點對應的結合面相對位移為

(10)

當結合面相對位移超過qmax時，則判斷系統進入宏觀滑移狀態，恢復力用式(5)第2式計算。

2.2 遲滯回線卸-加載轉折點

遲滯回線中卸-加載轉折點即系統相對速度為零時刻，判斷式為

(11)

即當i與i+1時刻速度符號相反、兩者乘積滿足小于等于零，且要求i+1時刻速度不等于零時，則i時刻為卸-加載轉折點。由于數值仿真中采用固定步長，式(11)判斷的轉折點僅為近似轉折點，但系統分析步長足夠小時，近似誤差亦小。

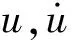
(12)

當ε=0時，式(12)線性系統稱為式(7)的派生系統，其中ωo為派生系統固有頻率，ω為外激勵頻率。ωo接近外激勵頻率ω時(ωo≈ω)，系統存在主共振現象；ωo接近外激勵頻率ω的1/2時(2ωo≈ω)，系統發生強烈1/2次亞諧波共振現象。引入比值變量Ω=ω/ωo，取Ω=1，Ω=2分別研究系統主共振及1/2亞諧波共振下混沌形態。每類情況下分別選α=0(不考慮線性剛度項)與α=0.5兩種，對比分析發生宏觀滑移后系統剩余剛度對混沌形態影響。

令時間τ為第三維，將式(9)平面非自治非線性系統擴維成三維，得系統龐加萊截面為

(13)

建立τ=0時初值點及其按解的路徑經時間2π/Ω后所達點間之關系。即主共振與1/2亞諧共振下系統平衡點附近的龐加萊映射。進一步將系統離散成龐加萊點映射系統為

gi+1=y(gi)

(14)

(15)

3 結果與討論

3.1 1∶1共振

α=0時，圖3(a)～(d)給出典型參數值下系統龐加萊截面。全局分岔見圖7(a)。由圖3可知，ge在零點附近激勵幅值量級較小不足以使滑塊單元產生滑動，系統非線性不明顯。在微小擾動下僅存在s+，s-兩段實時變化的互異雙曲型平衡曲線(圖3(a) 龐加萊映射)反對稱落在q=0軸兩邊；ge繼續增大，龐加萊截面上兩曲線段在ge=2處螺旋式趨于各自與之同側的互異雙曲平衡點s+，s-(圖3(b)龐加萊映射)，此處兩平衡點穩定流形Ws(s+)，Ws(s-)與不穩定流形Wu(s+)，Wu(s-) 滿足：Ws(s+)∩Wu(s-)≠0，或Ws(s-)∩Wu(s+)≠0，即重合后形成不變流形，由此斷定ge=2為異宿點；異宿軌道上點當τ→+∞及τ→-∞時分別趨近于各自不同的s+，s-。上述流形穩定性判別可據Peixoto[12]定理；由于該系統不同雙曲鞍點s+，s-的穩定流形Ws(s+)，不穩定流形Wu(s-)橫截相交于ge=2點，則該點亦稱為橫截異宿點，可通過Melnikov[13]方法判定。ge逐漸增大到2.07，龐加萊截面上平衡點(周期解)個數突增至6個，圖7(a)拓撲分支與圖3(c)說明經叉式分岔打破原穩定平衡解。ge=2.5時，系統由P6周期軌道過渡到混沌帶，圖3(d)～(f)分別為該點的龐加萊映射、功率譜、吸引子；之后系統重復經歷P2→混沌過程；可見，系統伴隨剛度減小及彈塑性過程的不斷交替，最終出現混沌運動原因為橫截異宿點的產生，此時雙曲鞍點穩定流形與不穩定流形為不同吸引子的吸引域邊界，與不穩定流形橫截相交后變為極復雜從而成為分形邊界，使運動具有極端敏感性。

圖3 龐加萊截面、功率譜及吸引子

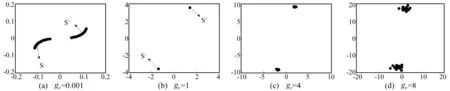
圖4 龐加萊截面

α= 0.5時，與α=0對比發現，最初小擾動下系統仍存在s+，s-兩個實時變化的互異雙曲型平衡曲線段見圖4(a)，反對稱落在q=0軸兩邊，較α=0早于ge=1處開始螺旋式趨于與之同側的互異雙曲平衡點s+，s-，見圖4(b)。同理可驗證ge=1為異宿點，但異宿軌道上點τ→-∞時，趨近于s+，s-；而τ→+∞時，軌線上點不再趨近于s+，s-，而發散開形成多倍周期Pn軌道，龐加萊截面上呈現多個離散點見圖4(c)～(d)；由此判斷ge=1非橫截異宿點。全局分岔見圖7(b)，系統始終未出現混沌軌道；因此，線性剛度項對系統動力學行為影響至關重要。

3.2 1∶2共振

α= 0時，微小擾動下零點附近存在s1，s2不變流形雙曲平衡點見圖5(a)。ge漸增至0.5，圖5(b)為兩個雙曲平衡點融合為s過程。此處穩定流形Ws(s)與不穩定流形Wu(s)滿足相交條件Ws(s) ∩Wu(s) ≠ 0直到ge≈0.8附近，螺旋式趨于完全融合的雙曲平衡點s，則上述集合中同宿點在ge≈0.8附近，此時對應的Ws(s)與Wu(s)彼此重合。同宿軌道上點τ→±∞時均趨近于一點s。

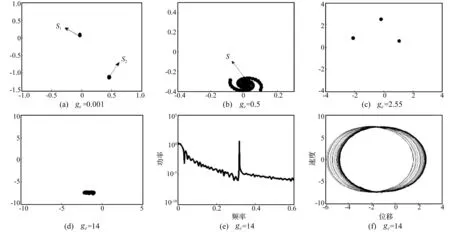
圖5 龐加萊截面、功率譜及吸引子

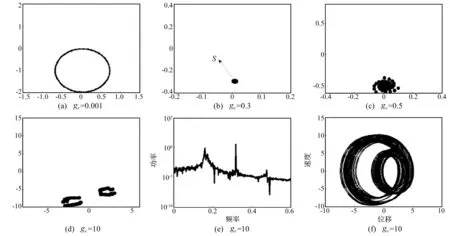
圖6 龐加萊截面、功率譜及吸引子

圖7(c)為區間[0,2]上分岔圖。該區間同宿分支點不止一個；因此推斷[13]，若存在同宿點s∈Ws(s) ∩Wu(s)，則s同時在Ws(s)，Wu(s)上。由于Ws(s)，Wu(s)均為不變流形，故對整數m,gm(s)也在Ws(s)，Wu(s)上，gm(s)為同宿點，必有無窮多同宿點存在，由此證明ge∈[0, 2]區間上不止一個同宿點，使該區間上不變流形異常復雜。ge=2.55時，龐加萊截面上平衡點個數突增至3個，系統經局部叉式分岔改變其拓撲結構，打破原穩定平衡態，變化過程見圖5(c)；之后循環出現3次叉式分岔，分別為ge=3.9處P3→P1，ge=4.1處P1→P3，ge=4.5處P3→P1。ge相對較大時系統出現柱狀混沌域。圖5(d)～(f)分別為ge=14時的龐加萊映射、功率譜及奇異吸引子。

α= 0.5時，與α= 0 對比發現，初始階段小擾動下龐加萊截面顯示準周期運動軌道見圖6(a)，ge=0.3處轉換為圖6(b)的穩定周期運動s，其穩定流形Ws(s)與不穩定流形Wu(s)彼此重合。同理ge=0.3點為同宿分岔點，s軌為同宿分岔軌道。同宿軌道上點τ→ ±∞時均趨近于s軌。圖7(d)說明在區間ge∈[0, 16]上不止出現一個ge=0.3的同宿分岔點。圖6(c)ge=0.5也為同宿點，說明α= 0中必存在無窮個同宿點使不變流形復雜程度提高，最終出現內嵌式混沌軌道。可通過圖6(d)～(f)在ge=10處的龐加萊映射、功率譜、奇異吸引子說明混沌現象。

圖7 全局分岔圖

4 結 論

以往簡單的干摩擦庫倫模型振子大多驗證通過周期倍化分岔、Hopf分岔及周期運動失穩等常見路徑通向混沌。本文在干摩擦振子基礎上，通過對多尺度粘滑摩擦振子混沌分析，結論如下：

(1) 考慮結合面的多尺度粘滑干摩擦情況存在的異宿、同宿分岔系統運動具有極端敏感性，小擾動下即可能出現混沌，從而驗證同宿、異宿軌道通向混沌的路徑，并表明龐加萊映射的雙曲鞍點穩定流形與不穩定流形是否相交與混沌運動是否發生密切相關。

(2) 系統在1∶1共振下因存在橫截異宿點，雙曲鞍點穩定流形、不穩定流形為不同吸引子的吸引域邊界，與不穩定流形橫截相交使系統拓撲結構異常復雜成為分形邊界，使運動具有極端敏感性，出現混沌。

(3) 系統1∶2共振下因存在無窮個同宿分支點，使不變流形異常復雜，系統受小擾動時，可能出現混沌運動。

[1] 朱華, 葛世榮.摩擦學系統的混沌特征[J].機械工程學報, 2004, 40(12):10-13.

ZHU Hua, GE Shi-rong.Chaotic characteristics of tribological systems[J].Chinese Journal of Mechanical Engineering, 2004, 40(12):10-13.

[2] 丁旺才, 張有強, 張慶爽.含干摩擦振動系統的非線性動力學分析[J].工程力學, 2008, 25(10):212-217.

DING Wang-cai, ZHANG You-qiang, ZHANG Qing-shuang.Nonlinear dynamics analysis of vibrate system with dry friction[J].EngineeringMechanics, 2008, 25(10):212-217.

[3] 白鴻柏, 黃協清.干摩擦振動系統響應計算方法研究綜述[J].力學進展, 2001, 34(4):527-534.

BAI Hong-bai, HUANG Xie-qing.An overview on study of methods of response computation for the dry frictionally damped vibration systems[J].Advances in Mechanics, 2001, 34(4):527-534.

[4] 丁千, 翟紅梅.機械系統摩擦動力學研究進展[J].力學進展, 2013, 43(1):112-131.

DING Qian, ZHAI Hong-mei.The advance in researches of friction dynamics in mechanics system[J].Advances in Mechanics, 2013, 43(1):112-131.

[5] 蔡力鋼，王鋒，李玲.栓接結合部動態特性研究進展[J].機械工程學報, 2013, 49(9): 158-168.

CAI Li-gang, WANG Feng, LI Ling.Review on dynamic properties of bolted joints[J].Chinese Journal of Mechanical Engineering, 2013, 49(9): 158-168.

[6] 劉麗蘭, 劉宏昭, 吳子英,等.機械系統中摩擦模型的研究進展[J].力學進展, 2008, 38(2):201-213.

LIU Li-lan, LIU Hong-zhao, WU Zi-ying,et al.An overview of friction models in mechanical systems[J].Advances in Mechanics, 2008, 38(2):201-213.

[7]Awrejcewicz J, Olejnik P.Analysis of dynamic systems with various friction laws[J].Applied Mechanics Reviews, 2005, 58:389-410.

[8] Segalman D J.Modeling joint friction in structural dynamics[J].Structural Control & Health Monitoring, 2006, 13(1): 430-453.

[9] Iwan W D.Thedynamic response of the 1-DOF bilinear hysteretic system[J].In: Proc.3rd World Conf.Earthquake Eng., New Zealand: University of Auckland, 1965, 2: 783- 796.

[10] Song Y.Modeling, identification and simulation of dynamics of structures with joints and interfaces[D].Urbana, Illinois: University of Illinois, 2004.

[11] Iwan, W D.Adistributed-element model for hysteresis and its steady-state dynamics systems[J].ASME Journal of Applied Mechanics, 1966, 33:893-900.

[12] Peixoto M C, Peixoto M M.Structural stability in the plane with enlarged boundary conditions[J].Acad., Brazil.Sci., 1959, 31:135-160.

[13] 楊紹普, 申永軍.滯后非線性系統的分岔與奇異性[M].北京: 科學出版社,2003.