輪式倒立擺的數學建模及狀態反饋控制
石 祥,許 哲,何青義,田 卡
(上海海洋大學 工程學院,上海 201306)
0 引言
倒立擺[1~3]作為一類非線性控制系統的典型特例,能有效地反映諸如可鎮定性、魯棒性、隨動性以及跟蹤等許多控制中的關鍵問題,是檢驗各種控制理論的理想模型,目前已有多種控制算法[4~9]應用其中,但是在研究其控制算法之前都存在著建模問題。目前關于各種倒立擺的研究論文中所給出的數學模型中,通常沒有系統微分方程的推理過程,或者模型比較單一,尤其是輪式倒立擺。
輪式倒立擺又稱 “兩輪自平衡機器人[10]”,其模型是建立在由兩個車輪左右平行布置、可移動的小車車體上,每個車輪都與電機相連。當車體運動時,通過控制電機的轉速來控制車輪,使擺桿盡快地達到一個平衡位置,并且沒有大的振蕩。當擺桿到達期望的位置后,系統能克服隨機擾動而保持穩定的位置。本文將對輪式倒立擺進行數學建模,從而得出其狀態方程,并基于Matlab及ADAMS的聯合仿真對輪式倒立擺的狀態反饋控制加以驗證。
1 數學建模
1.1 直流電機的數學模型
輪式倒立擺由兩個直流電機驅動,本節主要推導直流電機的數學模型,圖1展示了機械載荷和直流電源的驅動,從直流電源得到的電能轉換為機械能,機械能再轉換為作用在直流電機上的載荷。
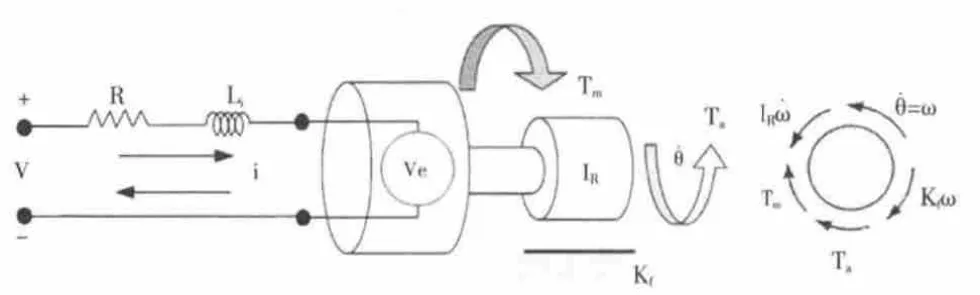
圖1 直流電機圖解Fig.1 Diagram of DC motor
因為軸上產生的所有扭矩與軸的加速度呈比例關系,而軸上的加速度又是通過電樞的轉動慣量IR產生,可推出如下關系:
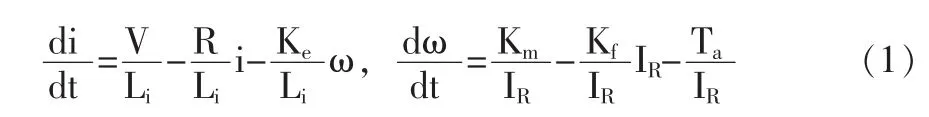
為了簡化直流電機模型,電機的電感和摩擦忽略不計,電流導數規定為零,因此式(1)可分別被等效成如下:
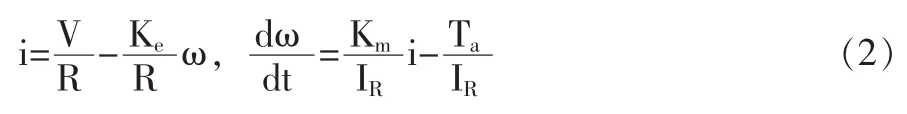
一旦輸入電壓改變,輸出軸的轉動速率也會改變,而此時電流將會達到一個瞬間恒定狀態,整理式(2)得:
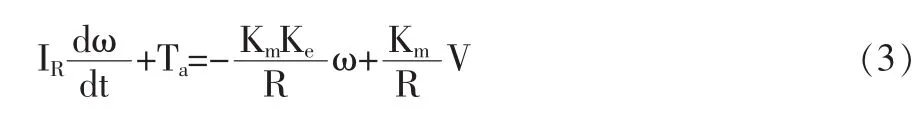
電機的輸入變量是外加電壓,電機的摩擦忽略不計,則電機扭矩方程如下:

1.2 輪式倒立擺的數學模型
輪式倒立擺分為車體和擺桿兩部分,將擺桿約束在二維平面,這樣更易于對其建模和控制,同時假設車輪總是與地面相接觸并且沒有產生滑動,這樣就沒有關于z軸方向的移動和繞x軸的轉動。
如圖2所示,輪式倒立擺三維坐標的定義。本文通過車體的位移量、車體的速度、擺桿的角度φ和擺桿的角速度φ˙作為狀態變量,直流電機的端電壓值作為輸入變量,以此描述輪式倒立擺的運動,得狀態方程。
(1)車輪的動態分析。根據牛頓運動定理,得到車輪左右兩輪的運動方程,右和左輪動態方程:
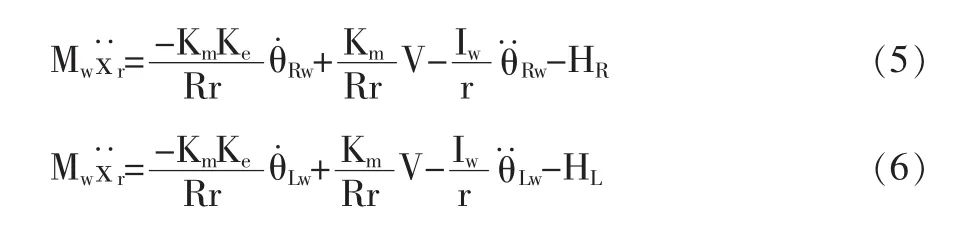
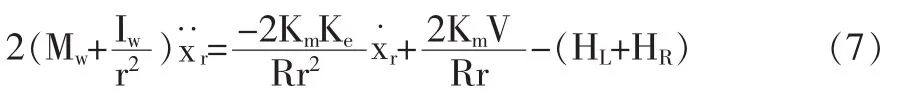
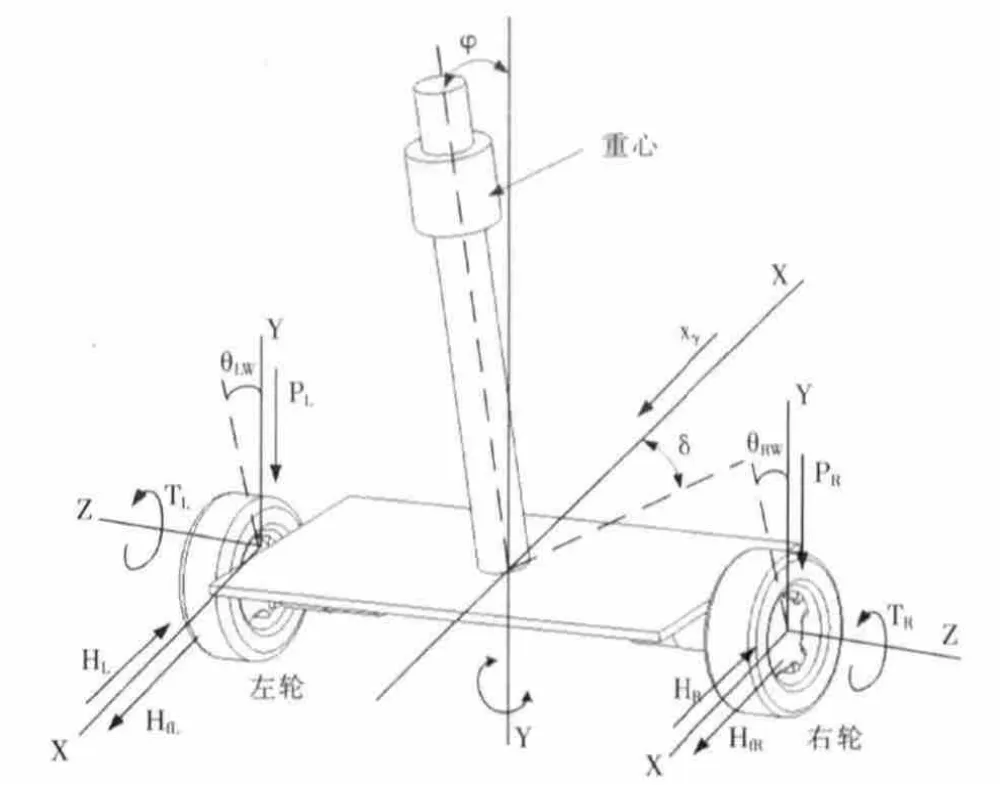
圖2 三維坐標的定義Fig.2 The definition of three-dimensional coordinates
(2)擺桿的動態分析。擺桿受力圖如圖3所示,其動態方程:
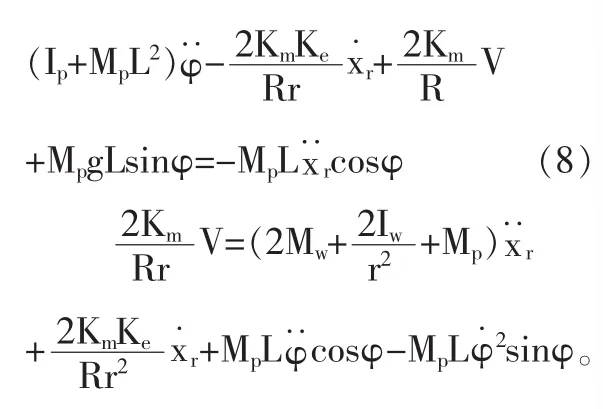
令φ=π+φ,使上述兩公式線性化,其中φ代表豎直方向上的小角度變化。 假設cosφ=-1, sinφ=-φ and則整理式(8)得:
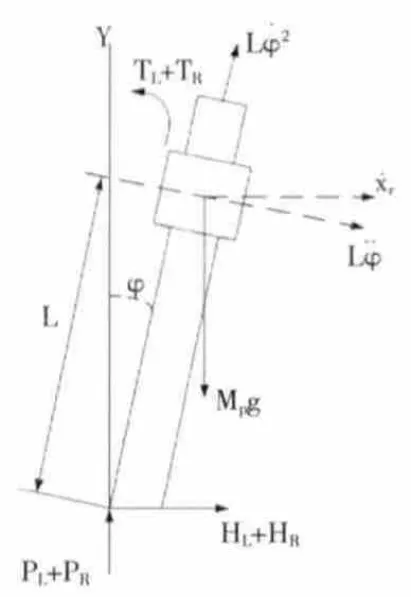
圖3 擺桿的受力圖Fig.3 Pendulum diagram
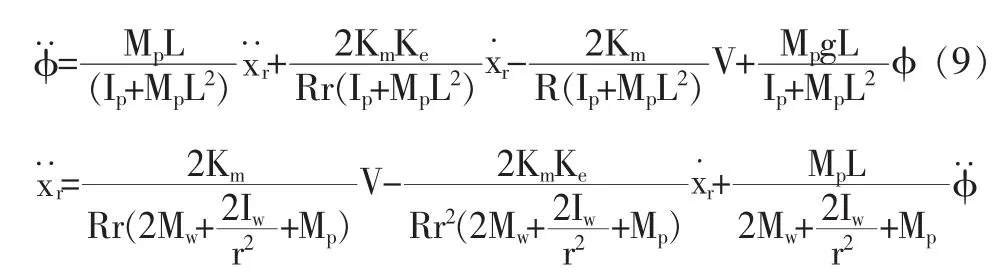
整理式(9)得狀態方程如下:

其中 a22, a23, a42, a43和 b2, b4根據如下系統的參數定義:
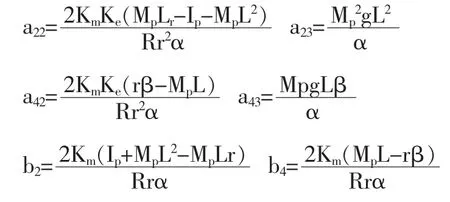
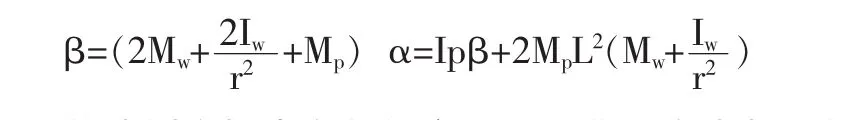
輪式倒立擺中參數的意義:V—作用在電機上的端電壓(V);Tm—電機產生的扭矩(N·m);Km—電機的扭矩系數,是電機產生的扭矩與電機內電流的比例系數(N·m/A)Ve—電機內部的反電動勢電壓(V);ω—電機軸的角速度(rad/sec); θ—電機軸的轉動角度(rad); Ke—反電動勢電壓系數,是電機的反電動勢電壓與電機軸角速度的比例系數(V·sec/rad);R—電機內的電阻(Ω); Li—電機的電感(H); IR—電機的轉動慣量(kg·m2); Kf—電機軸的摩擦系數(N·m·sec/rad); Tα—作用在電機軸上的負載扭矩(N·m);φ—擺桿繞Z軸的轉動角度(rad);xr—輪式倒立擺車體的位移(m);Mw—車輪質量(kg); HfR,HfL—車輪與地面的摩擦力(N)HL,HR—擺桿與車輪之間的作用力(N);Iw—車輪的轉動慣量 (kg·m2);θRw,θLw—右輪和左輪的轉動慣量(rad);TR,TL—右輪和左輪的負載扭矩(N·m);L—車體中心和擺桿重心之間的距離(m);Mp—擺桿質量(kg);r—車輪半徑(m);Ip—擺桿的轉動慣量(kg·m2);δ—擺桿繞 Y 軸的轉動角度 (rad), 其值為:g=9.81m/s2,r=0.051m,Mw=0.1272kg,Mp=0.86kg,Iw=0.000069kg·m2,Ip=0.0013kg·m2,L=0.07m,Km=0.006123Nm/A,Ke=0.006087V·sec/rad,R=3Ω。將以上參數帶入式(10)得:

2 Matlab 控制仿真
2.1 狀態反饋控制律設計
狀態反饋控制律為u=ξ-Kx,其中ξ—參考輸入。因為系統是能控的,則可以任意配置系統極點。經過調試,本文配置的系統極點為 [-10-11-20-25]。
Matlab 控制箱的place 函數, 能夠實現單輸入/多輸入系統極點配置,通過Matlab的place 函數,可求出反饋矩陣 K:K=[-0.0327-0.0092 1.0803 0.0692]·105。
綜上所述,K 和ξ確定之后,控制律u 便能確定。
2.2 仿真結果及分析
閉環系統的響應指標為:擺桿穩定時間小于5s,穩態時擺桿與垂直方向夾角小于0.1 弧度,程序采樣時間0.02s。仿真結果如圖4所示,表示狀態反饋控制律及系統響應,系統在初始位置不穩定,通過調節直流電機的端電壓,從而改變車體的位移和速度、擺桿的角度和角速度,系統在1 秒內,達到穩定狀態。仿真結果驗證了狀態方程、狀態反饋控制律和Matlab 仿真過程的正確性。
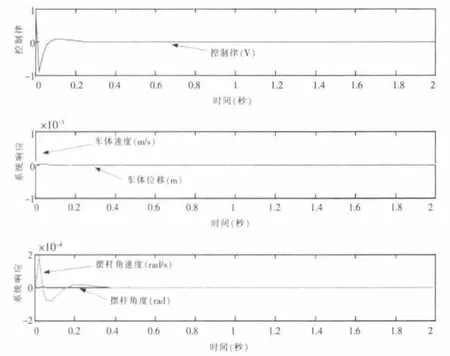
圖4 狀態反饋控制律及系統響應Fig.4 Control law and system response of state feedback control
3 Matlab與ADAMS的聯合仿真
3.1 聯合仿真簡介
為了更真實反映輪式倒立擺的實際動態過程,論文在ADAMS 中建立輪式倒立擺的虛擬樣機模型,在Matlab 中建立控制系統,其中控制系統將參考上述第二節,從而結合Matlab與ADAMS 進行聯合仿真,目的是更準確地顯示輪式倒立擺狀態反饋控制的特點。本章通過確定ADAMS的輸入和輸出變量,可以在ADAMS 和Matlab 之間形成一個閉合回路。ADAMS 模塊將車體的位移和速度、擺桿角度和角速度輸出給Matlab 控制系統,并根據這些變量計算出控制律u,將其輸入進ADAMS 模塊中,控制ADAMS 模塊中輪式倒立擺車輪上的轉矩,如此,二者之間形成循環反饋。
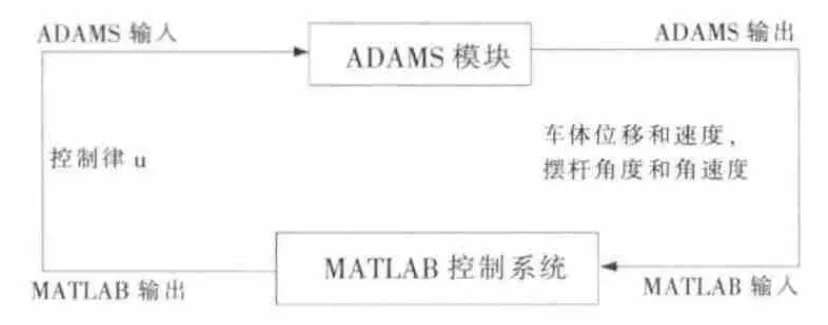
圖5 聯合仿真原理Fig.5 The principle of collaborative simulation
3.2 控制律的設計
在聯合仿真中,輪式倒立擺系統虛擬樣機模型,參數與上述一致,有關參數無需再次計算,只需作簡要調試。因此本章狀態反饋控制律,其反饋矩陣Γ調整為[-0.0032-0.0075 3.9823 1.9070]·104。
此外,上述第一節中提及輪式倒立擺的輸入變量為直流電機的端電壓值,而本章中虛擬樣機模型的輸入變量是車輪上的轉矩,兩者不一致,因此Matlab 控制系統在輸出控制律u 前,還需將電壓值轉為轉矩值。
3.3 仿真結果及分析
程序作圖采樣時間為0.005 秒,仿真結果如圖6所示。圖中表示輪式倒立擺的狀態反饋控制在初始位置不穩定時,通過調節車輪力矩的大小,在4 秒內,使車體位移、車體速度、擺桿角度和擺桿角速度收斂至0 附近,即輪式倒立擺平衡穩定。仿真結果表明狀態反饋控制能夠完成預期的控制目標,同時驗證了狀態反饋控制律和聯合仿真的正確性。
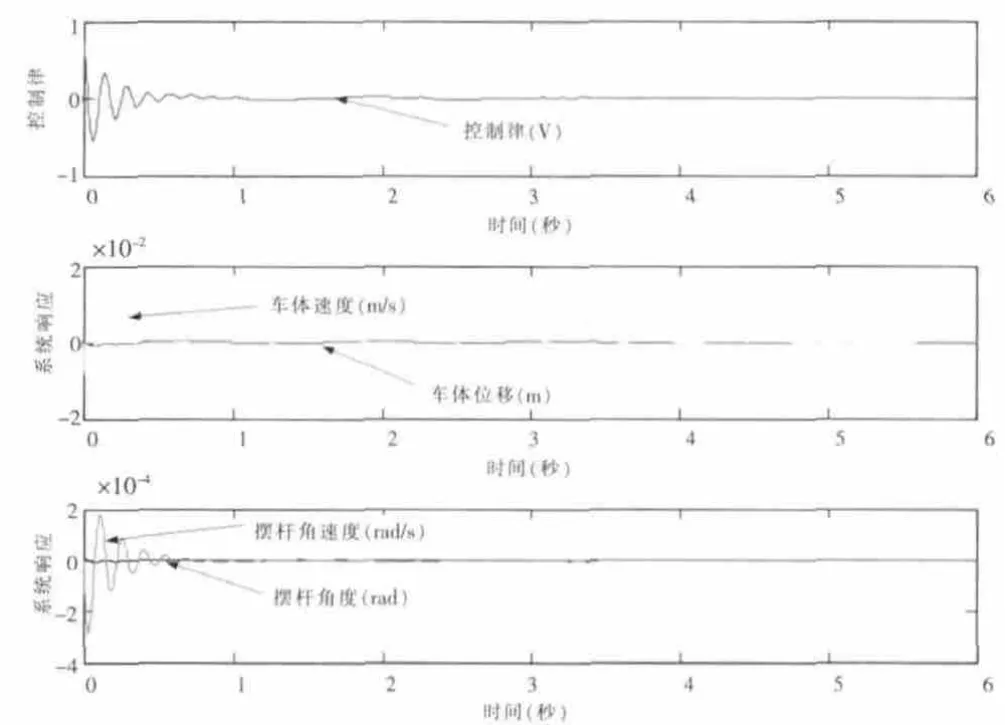
圖6 狀態反饋控制律和系統響應Fig.6 Control law and system response of State feedback control
4 總結
首先基于牛頓力學分析的方法,依次對直流電機、車體和擺桿進行動力學分析,列出其動力學方程,其次采用小角度線性化得出輪式倒立擺的近似線性模型。
由于輪式倒立擺的數學模型通常是線性化處理后得出,而倒立擺本身是高階非線性系統,那么二者之間必然存在偏差。所以本文不僅對輪式倒立擺進行Matlab 仿真,還對其進行Matlab與ADAMS的聯合仿真,目的是更為準確地表明輪式倒立擺狀態反饋控制的特點,最終,仿真結果不僅表明狀態反饋控制能夠使輪式倒立擺保持平衡,而且驗證了狀態方程、狀態反饋控制律、聯合仿真過程的正確性。
本文之所以在聯合仿真前,先進行Matlab 仿真,因為聯合仿真所涉及到的控制律,可以參考Matlab 仿真中設計出的控制律,這樣能極大地降低聯合仿真難度,其次,也可先行驗證輪式倒立擺狀態反饋控制的可行性。
[1]于占東,王剛,王顯峰.基于BVP 算法的旋轉倒立擺自動起擺動控制[J].控制工程,2013,1.
[2]王家軍,劉棟良,王寶軍.X-Z 倒立擺的一種飽和非線性穩定控制方法的研究[J].自動化學報,2013,1.
[3]但遠宏,李祖樞.二級倒立擺DU2UD的非線性控制研究[J].測控技術,2013,3.
[4]段學超,袁俊,滿曰鋼.兩輪自平衡機器人的動力學建模與模糊進化極點配置控制[J].信息與控制,2013,2.
[5]Z.Li,J.Luo(2009),“Adaptive robust dynamic balance and motion controls of mobile wheeled inverted pendulums”,IEEE Transactions on Control Systems Technology,17(1).
[6]阮曉剛,蔡建羨,陳靜.基于強化學習規則的兩輪機器人自平衡控制[J].計算機測量與控制,2009,2.
[7]C.W.Tao,J.S.Taur,T.W.Hsieh and C.L.Tsai(2008),“Design of a fuzzy controller with fuzzy swing-up and parallel distributed pole assignment schemes for an inverted pendulum and cart system”,IEEE Control Systems Technology,16(6).
[8]D.S.Nasrallah,H.Michalska and J.Angleles(2007),“Controllability and posture control of a wheeled pendulum moving on an inclined plane”,IEEE Transactions on Robotics,23(3).
[9]A.Casavola,E.Mosca and M.Papini(2004), “Control under constraints:An application of the command governor approach to an inverted pendulum”,IEEE Control Systems Technology,12(1).
[10]TIRMANT H,BALOH M,VERRNEIREN L.B2, “An alternative two wheeled vehicle for an automated urban transportation system”,IEEE.2002,39(4).

