液力偶合器額定工況流場數值計算

何延東

(遼寧石油化工大學機械工程學院,遼寧撫順113001)

0 引言

液力偶合器內部流動為非常復雜的粘性、三維、非定常氣液兩相流動，本文借助CFD軟件平臺對調速型液力偶合器額定工況下不同充液率的流場進行數值計算，得到偶合器內部速度與壓力分布，以及不同充液率下流場結構的變化及兩相分布情況，揭示其流場的流動規律和特性。

1 控制方程

偶合器內部為湍流流動，故應用連續方程、時均化雷諾方程和k-ε湍流模型，則有:

式中:εm——渦粘性系數；

V——流體質點速度矢量；

F——單位質量力；

p——壓力；

μ——動力粘度；

k——湍流能量；

ε——湍流能量耗散率；

cμ——系數，常取 0.09。

k和ε的運輸方程為:

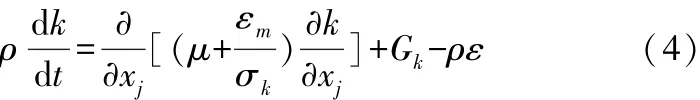
其中

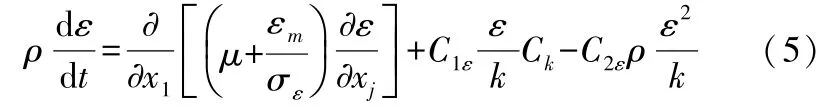
式中常數一般取:σk=1.0；C1ε=1.44；C2ε=1.92；σε=1.3。

流體在偶合器內作氣液三維粘性兩相流動的連續方程為:

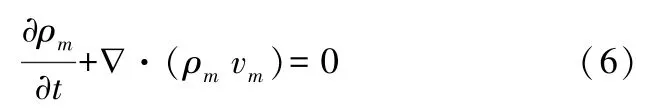
其中:

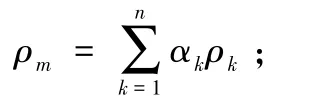
vm—質量平均速度；

ρm——混合密度；

αk——第k相的體積分數。

兩相流動的動量方程可以通過對所有相各自的動量方程求和來獲得。可表示為:

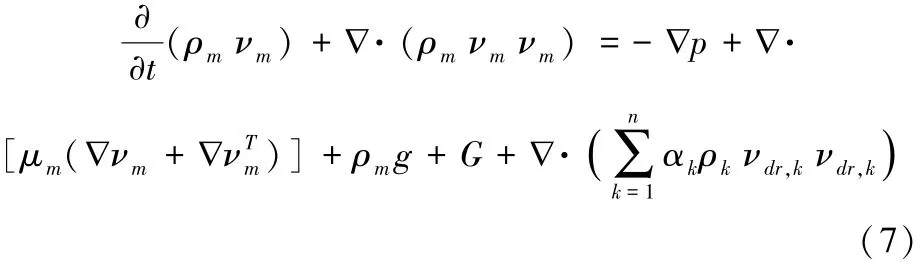
其中

n——相數；

G——體積力；

?——哈密爾頓算子；

μm——混合粘性。

第二相p的體積分數方程為:

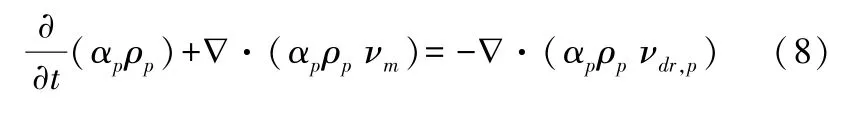
2 CFD建模

根據已有的偶合器有機玻璃模型進行三維建模，圖1為CFD計算模型和網格模型。

圖1 流道的計算模型和網格模型

液力偶合器的內部流動是非穩態的，而且泵輪流道與渦輪流道之間存在強烈的相互作用，為統一計算，對泵輪流道與渦輪流道的交界面采用滑動網格理論，將泵輪流道和渦輪流道統一計算。

滑動網格技術是一種非定常計算方法，它用到兩個或多個網格區域，每個網格區域至少有一個邊界的分界面，該分界面區域與另一網格區域相鄰。相鄰網格區域的分界面相互聯系形成“網格分界面(Grid-interface)”，簡稱Interface(交界面)，如圖2所示。計算過程中，單元區域沿著網格分界面相對滑動，而兩個區域的網格不會發生變化。當泵輪轉動時，泵輪與渦輪網格區域相對Interface產生滑移，交界面上信息按照滑移理論進行傳遞。

3 流場分析

3.1 整體流場分析

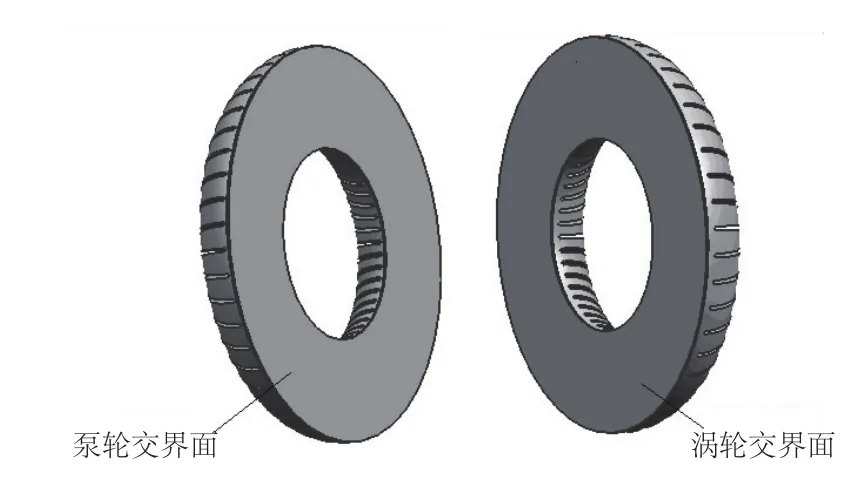
圖2 滑動網格邊界設置

3.1.1 整體流場壓力分布

圖3為不同充液率液力偶合器整體流場的壓力分布圖。額定工況下泵輪與渦輪的轉速差很小，相應的循環流量也很小，因此泵輪與渦輪流道的壓力分布非常具有規律性，沿徑向成比例逐漸增加，在泵輪出口與渦輪入口處達到最大。同時流道內循環流量較小，速度的變化也較小，使得速度對壓力變化的作用降低；粘性作用與偶合器的液力損失有關，額定工況下，能量損失很小，因此粘性作用對壓力變化的作用也不大。綜上所述，額定工況下后兩者的作用逐漸降低，那么離心力的作用就越來越重要，因此壓力的分布會呈現沿徑向比例分布的趨勢。在離心力的作用下，葉片的高壓區出現在葉片上部與外環的交界區域。小充液率時的低壓區高于大充液率，二者的高壓區分布大小相近。額定工況下壓力值比較小，而且壓力分布比較均勻，充液率的不同對壓力值有較大影響。

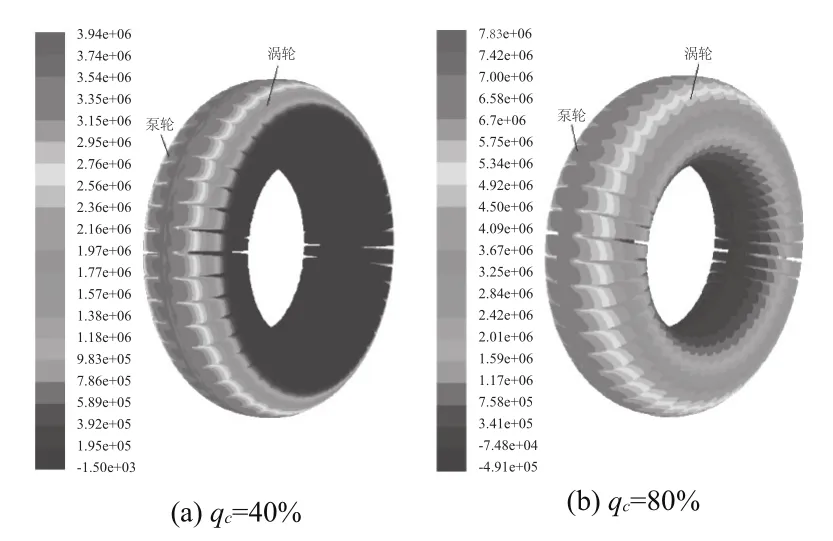
圖3 整體流場壓力分布圖

3.1.2 整體流場速度分布

圖4為不同充液率下的整體流道速度分布。由圖4可以看到，此時液流為大循環流動。泵輪與渦輪的速度分布非常具有規律性，速度值沿徑向成比例逐漸增加，流道中心處流速較低，泵輪出口與渦輪入口處為流道的高速區。與壓力分布不同的是，兩種充液率下的速度分布相近。對比不同充液率下偶合器的流場速度分布，可見充液率的不同對速度的大小沒有較大影響。額定工況下泵輪與渦輪的速度相差不大，這樣使得二者的流動較為順暢，沒有出現不規則流動現象。

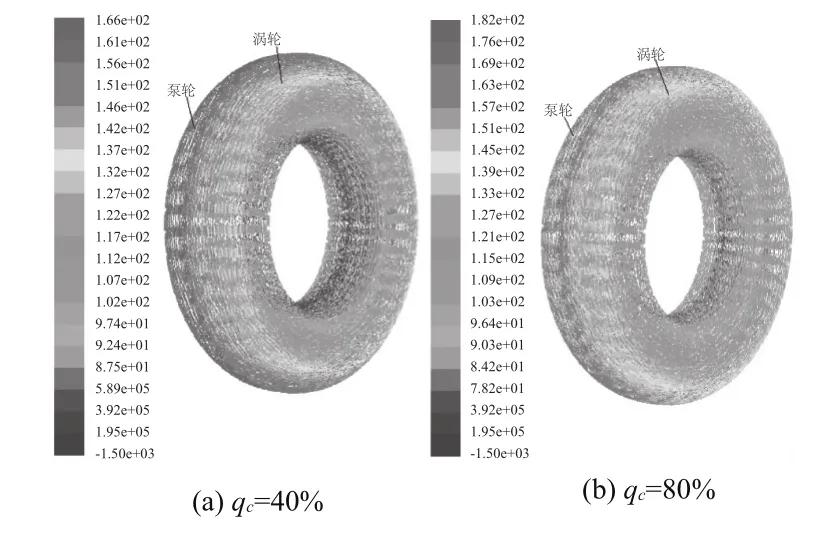
圖4 整體流場速度分布圖

3.1.3 液相體積分布

圖5所示為液力偶合器在不同充液率下的液相體積分布。對比圖5(a)、(b)可以發現，充液率為40%時，液體全部集中在偶合器的外環上部，流道的大部分空間被氣相所占據，充液率為80%時，氣體只集中在流道的中心區域。

圖5 液相體積分布圖

3.2 軸面流場分析

3.2.1 葉片壓力面流場分析

圖6所示為不同充液率時泵輪與渦輪葉片壓力面的壓力分布情況。從圖6中可以看出，葉片壓力面的分布比較有規律，其值沿徑向逐漸增大，在泵輪出口與渦輪入口處壓力值達到最大。小充液率時的低壓區遠遠高于大充液率時的低壓區。大充液率的壓力分布由葉片下部向上部非常規律的沿徑向逐漸增加。對比圖6(a)、(b)發現充液率的不同對壓力大小有較大影響，充液率大的壓力差較大。

圖6 壓力面壓力分布圖

圖7 為葉片壓力面的速度矢量分布情況。可以看出，兩種充液率下的速度分布相同，下部液流速度小于上部，整體速度分布都逐漸趨于沿徑向成比例分布。泵輪與渦輪的速度分布比較平穩，沒有二次流等不規則流動的出現。

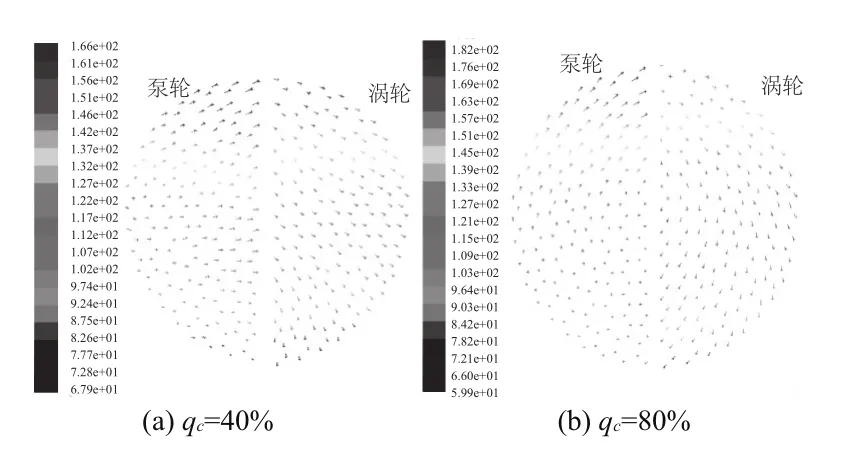
圖7 壓力面速度分布圖

3.2.2 葉片吸力面流場分析

圖8與圖9分別為額定工況下葉片吸力面壓力和速度分布圖。

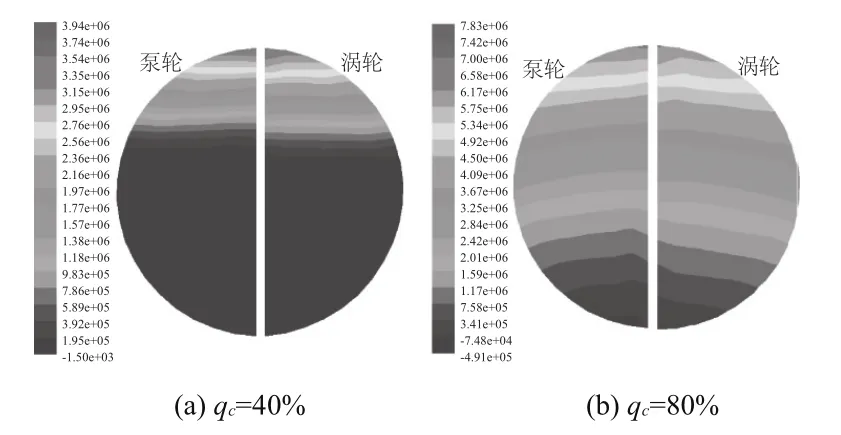
圖8 吸力面壓力分布圖

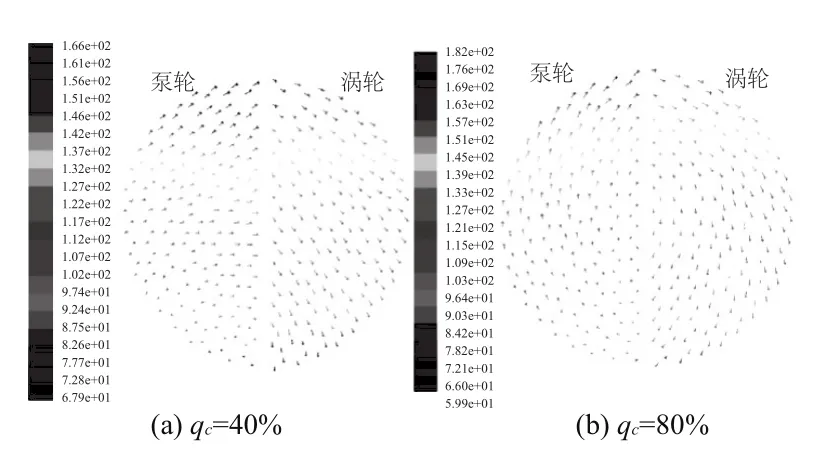
圖9 吸力面速度分布圖

從圖中可以看出葉片吸力面的壓力分布與速度分布和壓力面的分布相同，泵輪與渦輪流道的壓力與速度分布具有一定的規律性，壓力值與速度值沿徑向成比例逐漸增大，均在泵輪出口與渦輪入口處達到最大。

3.2.3 中間軸面流場分析

如圖10所示，分別在泵輪與渦輪流道內的軸面內作剖面A-A、B-B，該剖面能夠顯示泵輪與渦輪中間軸面方向上的壓力場與速度場。

圖11與圖12分別為額定工況下中間軸面的壓力和速度矢量分布圖。

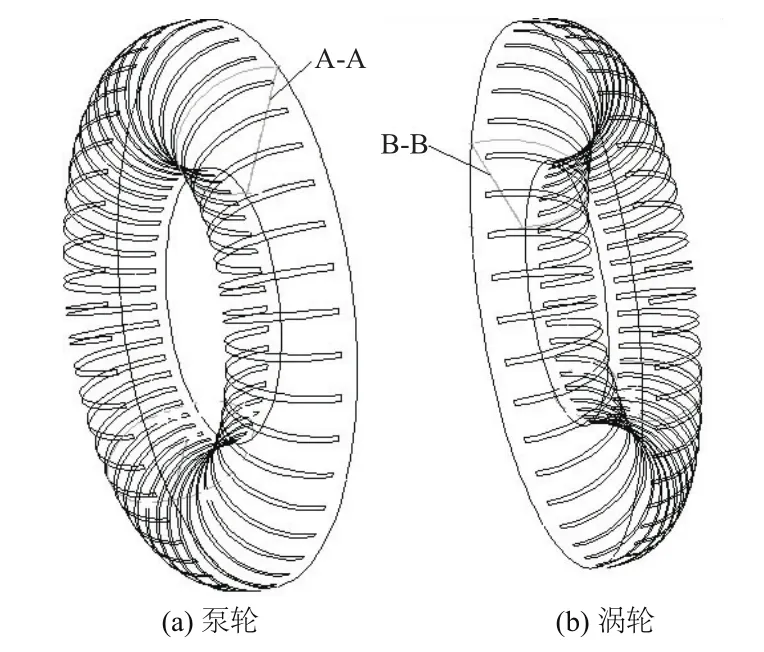
圖10 中間軸面示意圖

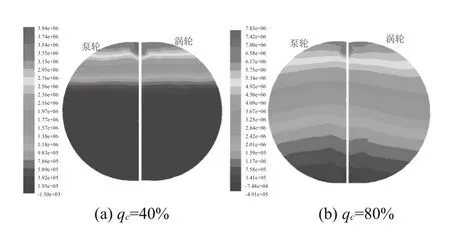
圖11 中間軸面壓力分布圖

圖12 中間軸面速度分布圖

從圖11中可以看出，額定工況下能量損失降低，粘性作用對壓力變化的作用也降低，離心力的作用越來越重要，因此壓力分布會呈現沿徑向比例分布的趨勢，且呈帶狀分布，在離心力的作用下葉片的高壓區出現在葉片上部與Interface的交界區域。低充液率下中間軸面的低壓區較大。

從圖12中可以看出，不同充液率下的速度分布沿徑向逐漸增加。由于額定工況下泵輪與渦輪速度轉速差較小，可以看到中間軸面的速度方向為泵輪與渦輪的旋轉方向，沒有出現偏向渦輪的分速度。不同的是，低充液率下的高速區分布范圍大于高充液率。

3.3 Interface流場分析

圖13與圖14分別為不同充液率Interface的壓力和速度分布情況。

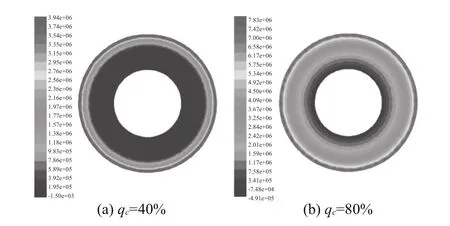
圖13 Interface壓力分布圖

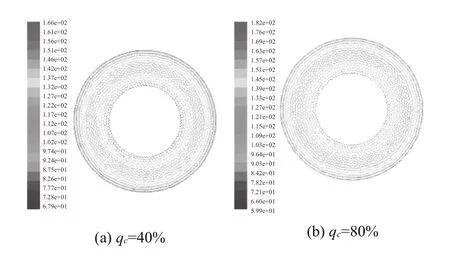
圖14 Interface速度分布圖

圖13 中(a)、(b)對比可知，高壓區出現在 Interface的外環，即泵輪出口與渦輪入口區域，低壓區出現在內環，即渦輪出口與泵輪進口區域。不同的充液率對Interface的壓力分布有較大影響，充液率小時低壓區域明顯多于大充液率區域，因此大充液率的總體壓力值較大。

從圖14中可以看出，不同充液率下Interface的速度分布完全相同，且沿徑向逐漸增大，在Interface的內環速度最小，外環速度最大，即泵輪出口區域和渦輪入口區域的速度達到最大值。

4 結語

對調速型液力偶合器額定工況下不同充液率時葉輪葉片與整體流道的流場進行數值計算與分析，初步揭示了偶合器在額定工況兩相流場的速度和壓力分布情況，數值模擬的結果基本反映了流道內部流動的基本特征。CFD計算可以應用于液力偶合器的設計，從而改變傳統設計方法需多次試制方可定型的弊端，在計算機上實現設計過程，達到準確、省時和省力的目的。

[1]萬天虎，趙道利，梁武科，等.基于CAD/CFD分析系統的流體機械翼型優化[J].流體機械，2005，33(11):37-39.

[2]余志毅，曹樹良，王國玉.葉片式混輸泵內氣液兩相流的數值計算[J].工程熱物理學報，2007，28(1):46-48.

[3]才委，馬文星，劉春寶，等.基于三維流場計算的液力變矩器特性預測方法[J].哈爾濱工程大學學報，2007，28(3):316-319.

[4]項昌樂，肖榮，閻清東，等.牽引-制動型液力變矩器流場分析[J].工程機械，2005(5):43-46.

[5]何志霞，袁建平，李德桃，等.柴油機噴嘴噴孔內氣液兩相湍流場三維數值模擬[J].內燃機工程，2005(6):18-21.

[6]盧金鈴，席光，祁大同.離心泵葉輪內氣液兩相三維流動數值研究[J].工程熱物理學報，2003(2):237-240.

[7]李雪松，馬文星，吳允柱.液力偶合器制動工況三維流場數值模擬及制動轉矩計算[C].第四屆全國流體傳動及控制學術會議論文集.大連，2006:659-664.