具有湍流效應的不規則微下擊暴流構建方法研究
劉時杰, 徐浩軍, 薛源, 張久星
(空軍工程大學 航空航天工程學院, 陜西 西安 710038)
0 引言
微下擊暴流屬于下沖氣流的一種,是以垂直風切變為主要特征的復雜風切變區域[1-2]。研究微下擊暴流對于飛機起飛、著陸時的飛行品質分析與飛行安全保障具有重要的意義。微下擊暴流模型的研究目前有多種方法,例如利用基于風洞實驗與CFD數值計算的方式研究其速度場分布[3-4],以及基于融合重疊的方法[5]和基于渦環原理的方法[6-8]。其中Woodfield和Woods[6]最早提出的渦環原理模型是目前應用最廣泛的一種微下擊暴流模型。
目前的方法所構建的微下擊暴流模型多為沿中心軸對稱的規則形狀,但實際的微下擊暴流風場非常復雜,其下沉氣流并不一定垂直于地面,其外流范圍也不是軸對稱的,且一個區域內可能伴隨有多個風暴核,甚至還有局部上升氣流。并且在其風速的分布范圍內亦可能伴隨有其他大氣流動狀況,如不規則突風與飛機尾流產生的湍流。故本文擬在構建不規則微下擊暴流模型的基礎上考慮突風與湍流的影響,為起飛、著陸與低空飛行時的安全性仿真提供更加準確的風場輸入條件。
1 不規則微下擊暴流風場建模
1.1 單個渦環誘導下的風場構建
首先利用渦環原理構造微下擊暴流風場模型。依據美式坐標系,建立一個如圖1所示的渦環模型。在地面處,風速垂直方向的分量為0。通過在地面上方布置一個強度為Γ的主渦環,同時在對稱下方布置一個強度為-Γ的鏡像渦環,即可滿足地面垂直速度為0的邊界條件。圖1中,主渦環中心在P(xP,yP,zP)處,鏡像渦環中心在(xP,yP,-zP)處。,R為渦環半徑,A為空間中某點,坐標為(xA,yA,zA)。
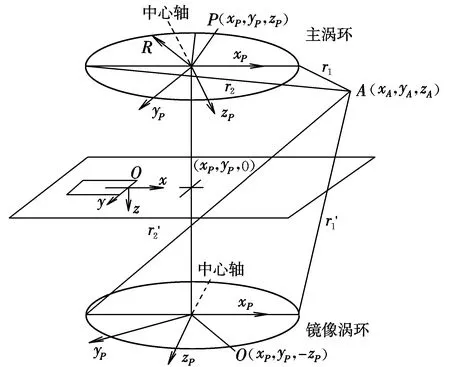
圖1 單渦環示意圖Fig.1 Single vortex ring
首先討論單渦環影響下的微下擊暴流場構建方法,當渦環面與地面平行時,渦環的流線方程為:
ψ=-(Γ/2π)(r1+r2)[F1(k)-F2(k)]
(1)
式中,Γ為渦環強度;r1為A點距渦環距離最近的距離;r2為A點距渦環最遠點的距離;k=|(r2-r1)/(r2+r1)|;F1(k)與F2(k)為圓環的積分函數。若0≤k2≤1,則:
(2)
將式(2)代入式(1),獲得主渦環的流線方程為:
(3)
鏡像渦環的流線表達式為:
(4)
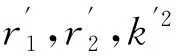
最終將主渦環流線表達式與鏡像渦環流線表達式線性疊加,得到空間點A的流線方程為:
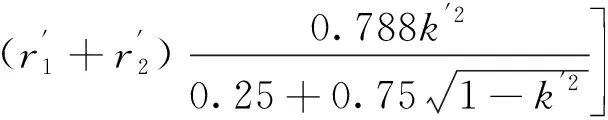
(5)
而后得到點A的誘導速度為:
(6)
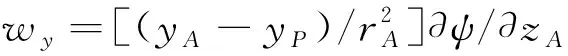
(7)
wz=(-1/rA)?ψ/?rA
(8)
式中,rA為點A距渦環對稱軸的距離。
1.2 中心軸處的誘導速度計算
在渦環的中心軸處rA=0,用式(6)~式(8)計算誘導速度會產生奇點。因此,通過引入渦環的位函數,利用式(10)計算垂直方向的速度wz;由于渦環沿中心軸的對稱性,水平速度wx和wy為0。
wz(z)=(Γ/2R)[1/(1+(z/R)2)3/2]
(9)
式中,z為中心軸上各點離渦環中心的距離。
1.3 渦核內部的誘導速度計算
根據式(6)~式(8),在渦環的中心渦絲處,流速趨于無窮大,這不符合微下擊暴流風場的實際情況。由于流體粘性的影響,實際渦環有一個渦核的存在,且渦核內速率逐漸減小,至渦核的中心渦絲處減為0。本文運用復合渦原理,將渦核看作半徑為r的圓柱,渦核內部的渦量均勻分布,保證渦絲處的流速為0,而渦核外部仍然服從流線方程。從渦核中心到渦核半徑處,流速呈線性分布,如圖2所示。
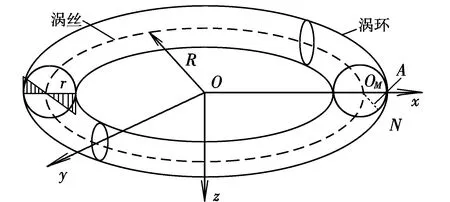
圖2 渦核內部誘導速度示意圖Fig.2 Velocity induced inside the vortex core
設渦核半徑為r,首先應該判斷點A(xA,yA,zA)是否在渦核內,若滿足下式,則點A在渦核內。
(rA-R)2+(zP-zA)2≤r2
(10)
根據點A的坐標、渦環中心的坐標求出與點A、渦環中心點共面的渦核絲坐標點O(xO,yO,zO)。再求出與點A、點O共線,與點A、渦核中心點共面的渦核外壁坐標N,如圖2所示。根據式(6)~式(8)求出坐標N的誘導速度,再根據點A、點N距離點O的距離按比例求出A點的誘導速度。
1.4 微下擊暴流風場的不規則變換
根據美式坐標系確定旋轉軸心為渦環的中心點處(見圖1),引入俯仰變換矩陣Lθ、滾轉變換矩陣Lφ、偏航變換矩陣Lψ,對坐標系及速度進行旋轉變換,從而構建不規則速度場。對于主渦環坐標系的變換公式為式(14),對于速度矢量的變換公式為式(15)。鏡像渦環的俯仰變換角度和滾轉變換角度與主渦環正負相反,偏航變換角度與主渦環相同。
(11)
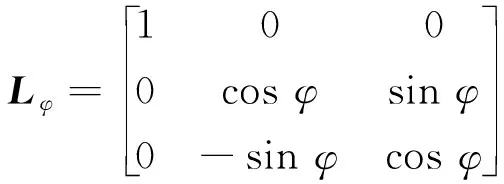
(12)

(13)
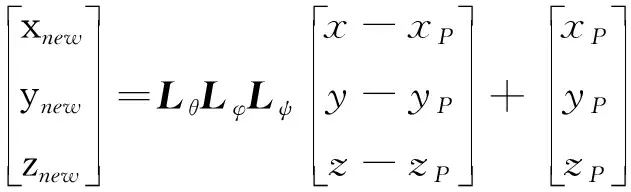
(14)

(15)
經過變換后的坐標排列亦是不規則的,因為飛行實時仿真需要根據微下擊暴流模型動態插值每個坐標點的速度矢量,故這種混亂不規則的坐標排列在飛行實時仿真中是無法使用的。故需將變換后坐標點對應的速度矢量擬合到標準的升序排列三維坐標點上,如式(16)。文中采用的擬合方法為線性插值法,由于坐標點較多,達到了100萬以上,故擬合計算的過程相對于其他步驟來說耗時較長。
(16)
將標準坐標系內的主渦環與鏡像渦環的誘導速度場相疊加,得到渦環1總的誘導速度場[wx1,wy1,wz1]。
1.5 多個渦環誘導風速的疊加
由于單個渦環誘導的微下擊暴流場垂直風速相對較小,為了更加逼真,通常使用多個渦環誘導微下擊暴流場。多個傾斜渦環疊加而成的微下擊暴流速度場為:
(17)
式中,[wxn,wyn,wzn]為第n個渦環的誘導速度場。
2 低空大氣湍流風場結構的構建
湍流風場采用Dryden模型[9]得到,其單側一維頻譜函數為:
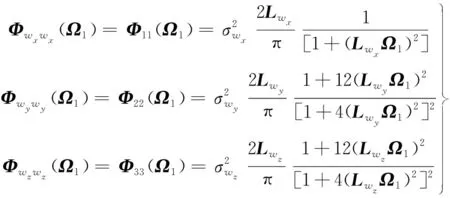
(18)
式中,Lwx,Lwy,Lwz為湍流尺度;σwx,σwy,σwz為湍流強度。文中Lwx=2Lwy=2Lwz=380 m,σwx=σwy=σwz=3.6 m/s。
在飛行實時仿真中,關鍵問題在于如何產生高保真度的大氣湍流。產生的湍流速度不僅要具有隨機性,還必須符合其頻譜特性。本文利用白噪聲通過一定形式的濾波器來產生湍流速度。白噪聲X(t)是一種具有特殊性質的隨機過程,它的頻譜函數等于常數,其相關函數為脈沖函數,如下式:
ΦXX(ω)=N0,RXX(τ)=N0δ(τ)
讓白噪聲X(t)通過一個傳遞函數為G(s)的環節,設其輸出為Y(t)。輸出Y(t)的頻譜函數為:
ΦYY(ω) =G*(iω)ΦXX(ω)G(iω)
=N0G*(iω)G(iω)
由上式可見,若要求輸出Y(t)具有特定的頻譜ΦYY(ω),應將ΦYY(ω)作因式分解為G*(iω)和G(iω)的乘積,從而找到濾波器應具有的傳遞函數G(s)。
以Dryden模型(式(18))的第一式為例進行因式分解。將其按空間頻率和時間頻率的轉換關系Φ(ω)=(1/v*)Φ(ω/v*)轉化為:
對其進行因式分解:
Φwxwx(ω)=
所以其對應的傳遞函數為:
同理可得Gwy(s)和Gwz(s)。
根據以上論述,三個方向的大氣湍流速度的產生如圖3所示。

圖3 湍流速度的產生Fig.3 Generation of turbulence velocity
將微下擊暴流速度場與尾流引起的湍流速度場在坐標系內進行線性疊加,從而得到受湍流效應影響的微下擊暴流速度場。
3 計算結果及分析
選擇三個渦環來構成不規則微下擊暴流風場,坐標范圍為x:0~6 km,y:0~6 km,z:0~0.8 km。第1個渦環的中心點坐標為(3.0,3.0,0.6)km,R=0.9 km,r=0.455 km,Γ=18 000 m2/s,俯仰偏角為15°,滾轉偏角為5°;第2個渦環的中心點坐標為(2.5,2.5,0.5) km,R=0.7 km,r=0.3 km,Γ=-10 000 m2/s,俯仰偏角為10°,滾轉偏角為-5°;第3個渦環的中心點坐標為(3.0,4.0,0.6) km,R=0.8 km,r=0.4 km,Γ=11 000 m2/s,俯仰偏角為25°,滾轉偏角為15°。所得結果如圖4~圖9所示。
從圖4~圖8中可以看出,相比于規則風場,文中對不規則微下擊暴流的構建是成功有效的,構建的風場不再沿軸線對稱,比較符合實際情況;并且由于加入了湍流的影響,速度場存在明顯的不規則湍動,較好地反映了低空大氣湍流對風場隨機性的影響。
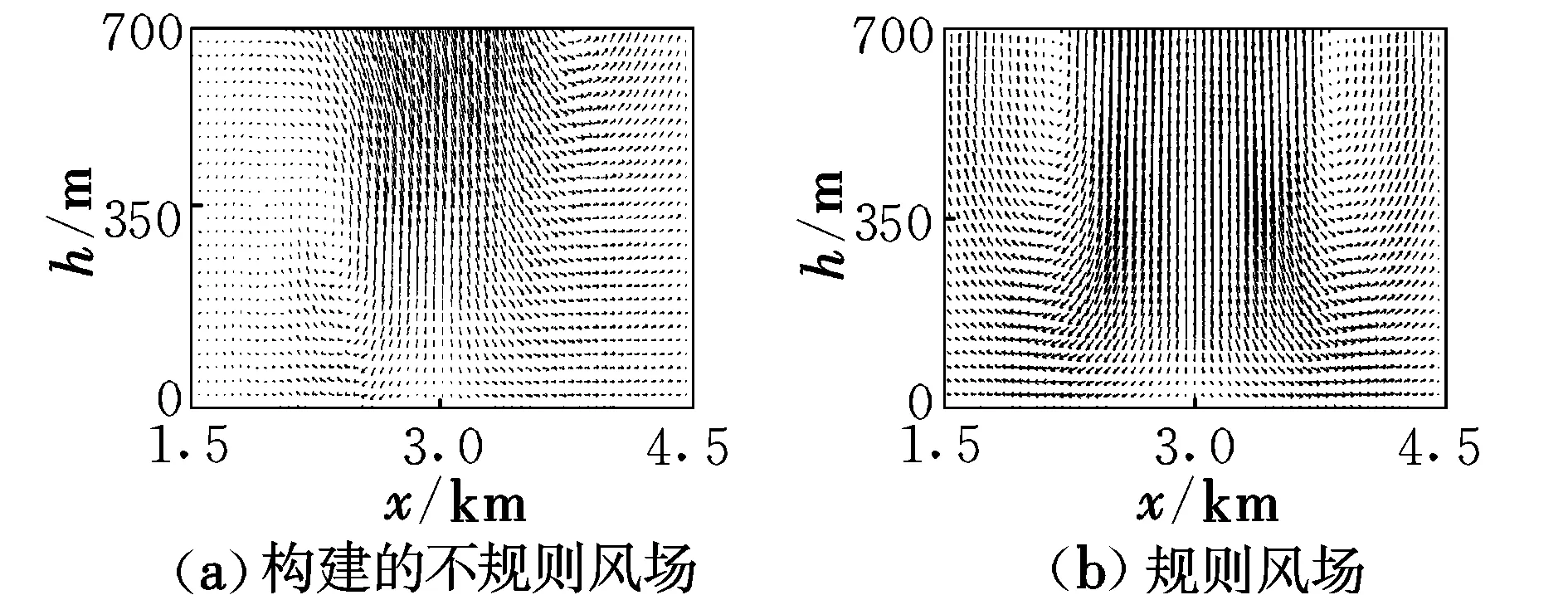
圖4 在剖面y=3 km上的風速矢量圖Fig.4 Wind speed vector on the profile y=3 km
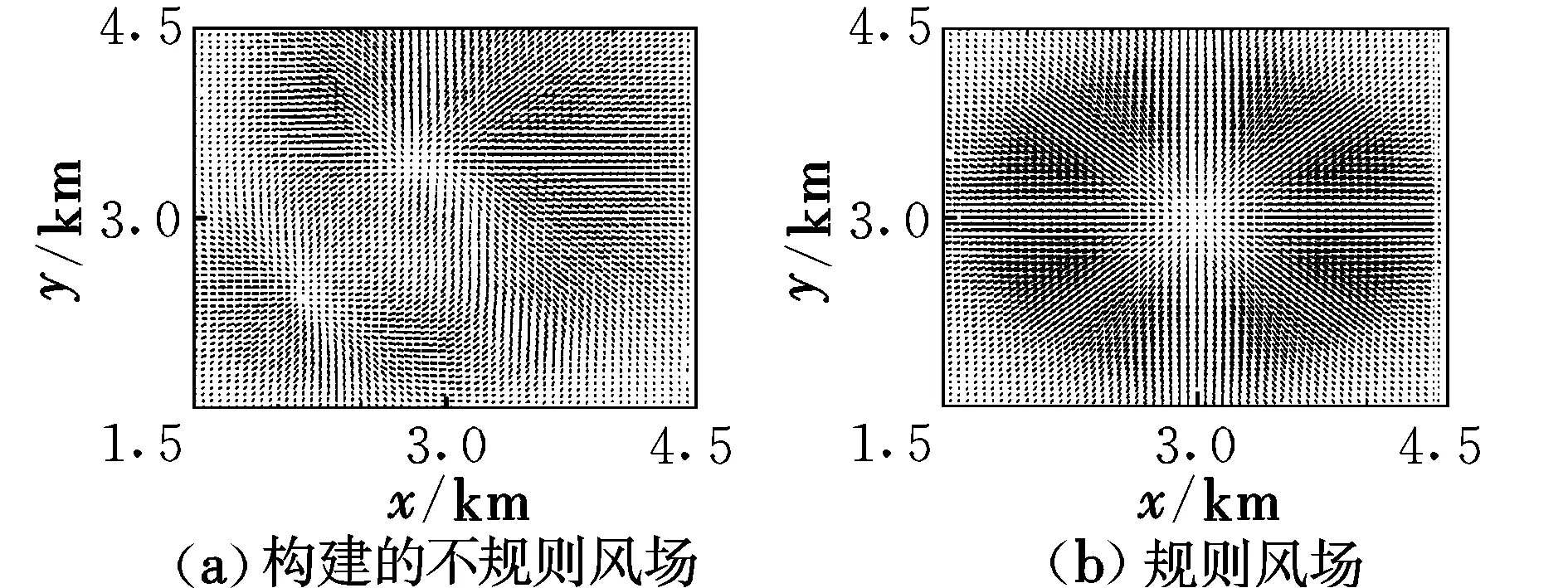
圖5 在剖面z=0.4 km上的風速矢量圖Fig.5 Wind speed vector on the profile z=0.4 km
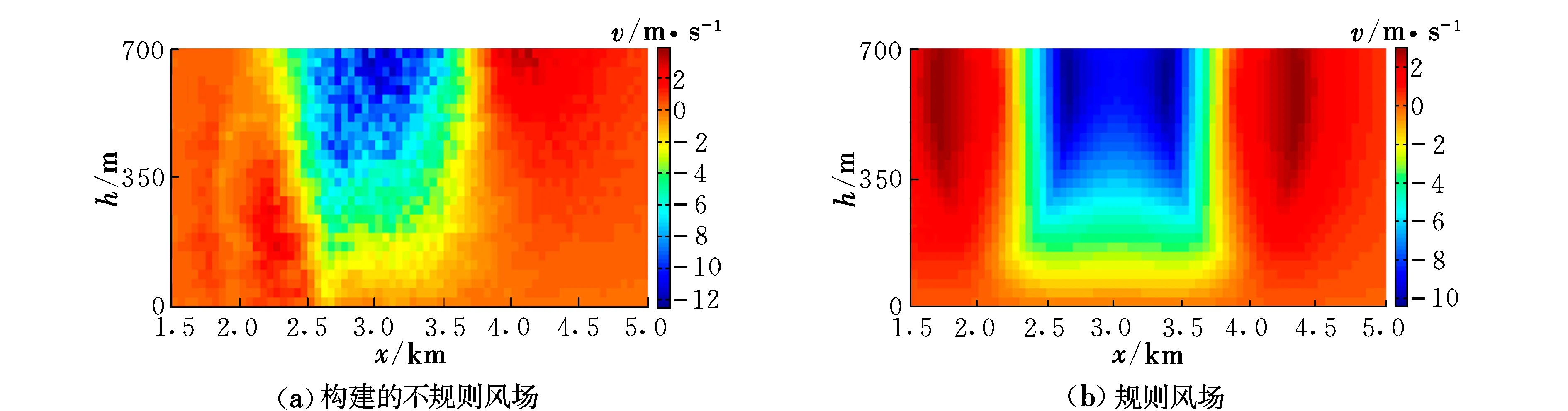
圖6 在剖面y=3 km上的wz云圖Fig.6 Cloud map of wz on the profile y=3 km
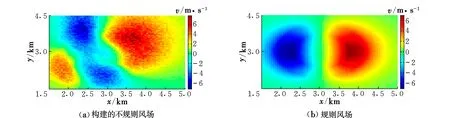
圖7 在剖面z=0.4 km上的wx云圖Fig.7 Cloud map of wx on the profile z=0.4 km

圖8 在剖面x=3.5 km上的wz云圖Fig.8 Cloud map of wz on the profile x=3.5 km

圖9 三維空間內wz=-5 m/s的拓撲結構圖Fig.9 Topology structure in the 3D space with wz=-5 m/s
4 結束語
本文綜合考慮了微下擊暴流的隨機性與不確定性,通過多渦環建模法構建了具有旋轉傾斜效應的不規則微下擊暴流速度場,并將其與低空大氣湍流相互疊加以反映風場在湍流作用下的隨機性。所得風場能較好地描述多因素耦合復雜情況下的大氣流動狀況,相比于以往對微下擊暴流速度場的研究更加深入、系統,也更接近復雜風場的實際情況。對于起飛、著陸階段飛行安全性仿真分析、復雜風場中的風險規避以及控制技術研究具有積極的意義,亦可以進一步補充完善大氣流動數據庫。
參考文獻:
[1] Fujita T T.Tornadoes and downbursts in the context of generalized planetary scales [J].Journal of Atmospheric Science,1981,38(8):1511-1534.
[2] 朱上翔.微下擊暴流的流體動力學模型[J].飛行力學,1984,2(2):59-72.
[3] Qu W,Ji B.Numerical study on formation and diffusion wind fields for thunderstorm microburst[C]//Proc.of the International Conference on Mechanic Automation and Control Engineering.U.S.:IEEE,2010:1389-1392.
[4] 瞿偉廉,王錦文.下擊暴流風荷載的數值模擬[J].武漢理工大學學報,2008,30(2):70-74.
[5] Nguyen H,Manuel L,Veers P.Simulation of inflow velocity fields and wind turbine loads during thunderstorm downbursts[R].AIAA-2010-2651,2010.
[6] Woodfield A A,Woods J F.Worldwide experice of wind shear during 1981-1982[R].ADP002705,1983.
[7] DoD.MIL-HDBK-1797 Military Handbook[S].U.S.:DoD,1997.
[8] DoD.MIL-F-8785C Military Specification[S].U.S.:DoD,1980.
[9] Yeager J.Implementation and testing of turbulence models for the F18-HARV simulation[R].NASA CR-1998-206937,1998.

