基于微分對策的追逃對抗仿真
車競, 鄭鳳麒
(中國空氣動力研究與發展中心 計算空氣動力研究所, 四川 綿陽 621000)
0 引言
微分對策理論是研究利益相互制約的雙方策略選擇的理性行為及相應結局的學科。1971年,美國科學家Friedman采用了兩個近似離散對策序列精確定義了微分對策,建立了微分對策與鞍點存在性理論,從而奠定了微分對策理論的數學基礎。
由于理論上的最優性,微分對策已廣泛應用于戰術導彈的制導律設計。Tahk等人[1]利用梯度法求解了微分對策制導的數值解,但模型非常復雜。Basar等[2]設計了離線的神經網絡微分制導律。湯善同[3]利用微分對策強迫奇異攝動方法設計了零階組合反饋制導律。羅生等[4]采用伴隨理論求解了終端控制的微分對策最優制導問題。空戰決策方面,“一對一”空戰通常可比擬為二人零和定量微分對策問題。梅丹等[5]利用微分對策方法建立了以捕獲時間tf為性能指標的二維單機追逃空戰的決策模型。王發坤等[6]建立了三維空間追逃問題的定性微分對策模型。由于微分對策模型是典型的兩點邊值問題,數值求解通常采用梯度迭代法。黃力偉[7]提出了將梯度法和靜態優化算法相結合的一類數值解法。泮斌峰等[8]通過終端時刻調節算法求解了終端時刻tf自由的兩點邊值問題。
本文應用微分對策理論,對縱向平面內導彈-飛機的追逃問題進行了研究,建立了數學模型,對于終端時刻tf自由的情況,通過內外環兩次迭代得到了數值解,針對有控制能量最小要求和無控制能量最小要求兩類性能指標下的微分對策模型,在雙方不同的最大機動能力條件下進行了數值仿真,其模型和仿真結果可用于空戰雙方武器性能、制導控制設計評估,以及最優空戰決策研究。
1 微分對策問題描述
對于攻防對抗的A和B雙方,組成n維系統[8]:
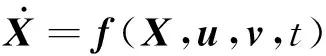
(1)
式中,u(t),v(t)分別為A,B雙方的控制向量。微分對策即要求解u(t)和v(t),使得在系統滿足終端目標集ψ(tf,X(tf))=0的情況下,對于A方,達到性能指標J最小;對于B方,達到性能指標J最大。性能指標通常采用如下形式:
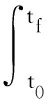
(2)
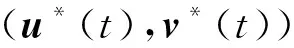
(3)
相應地,J*稱為最優對策值,X*(t)稱為最優跡線。
2 微分對策問題求解
2.1 求解基本方程
上述微分對策問題通常采用極小值原理進行求解,首先構造哈密頓函數:
H(X,λ,u,v,t)=L+λTf
(4)
式中,λ為哈密頓乘子,求解下述正則方程組可得到問題的最優解:
(5)
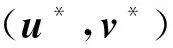
(6)
若終端時刻tf不固定,則還必須通過下述條件自然確定tf:
dJ/dt|tf=H(X*,λ*,u*,v*,t)|tf+?φ/?t|tf=0
(7)
2.2 數值計算方法
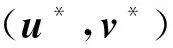
(1)置迭代步數i=0,j=0;
(3)任意選擇uj(t),vj(t)作為初始策略;
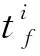
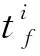
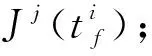
(8)更新控制量uj+1(t)=uj(t)-αgu(t),vj+1(t)=vj(t)+βgv(t)(α,β為無限小正數,由一維搜索算法確定),置j=j+1,返回步驟(4);
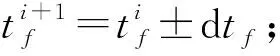
(10)檢查收斂:當dtf≤ε2時,終端時刻迭代收斂,算法結束,否則置i=i+1,返回步驟(3)。
3 導彈-飛機的數學模型
考慮一個縱向平面內的導彈-飛機追逃問題,雙方速度大小不變,速度方向的改變量為控制量,追逐方(導彈,用下標D表示)運動方程為:
(8)
式中,xD,yD,vD,θD分別為導彈的縱橫坐標、速度和傾角。逃避方(目標,用下標M表示)運動方程為:
(9)
式中,xM,yM,vM,θM分別為目標的縱橫坐標、速度和傾角。令:
(10)
得到雙方縱向平面內追逃系統的狀態方程為:
(11)
設性能指標(支付函數)為:
(12)
4 仿真結果及分析
4.1 仿真示例1
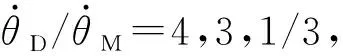
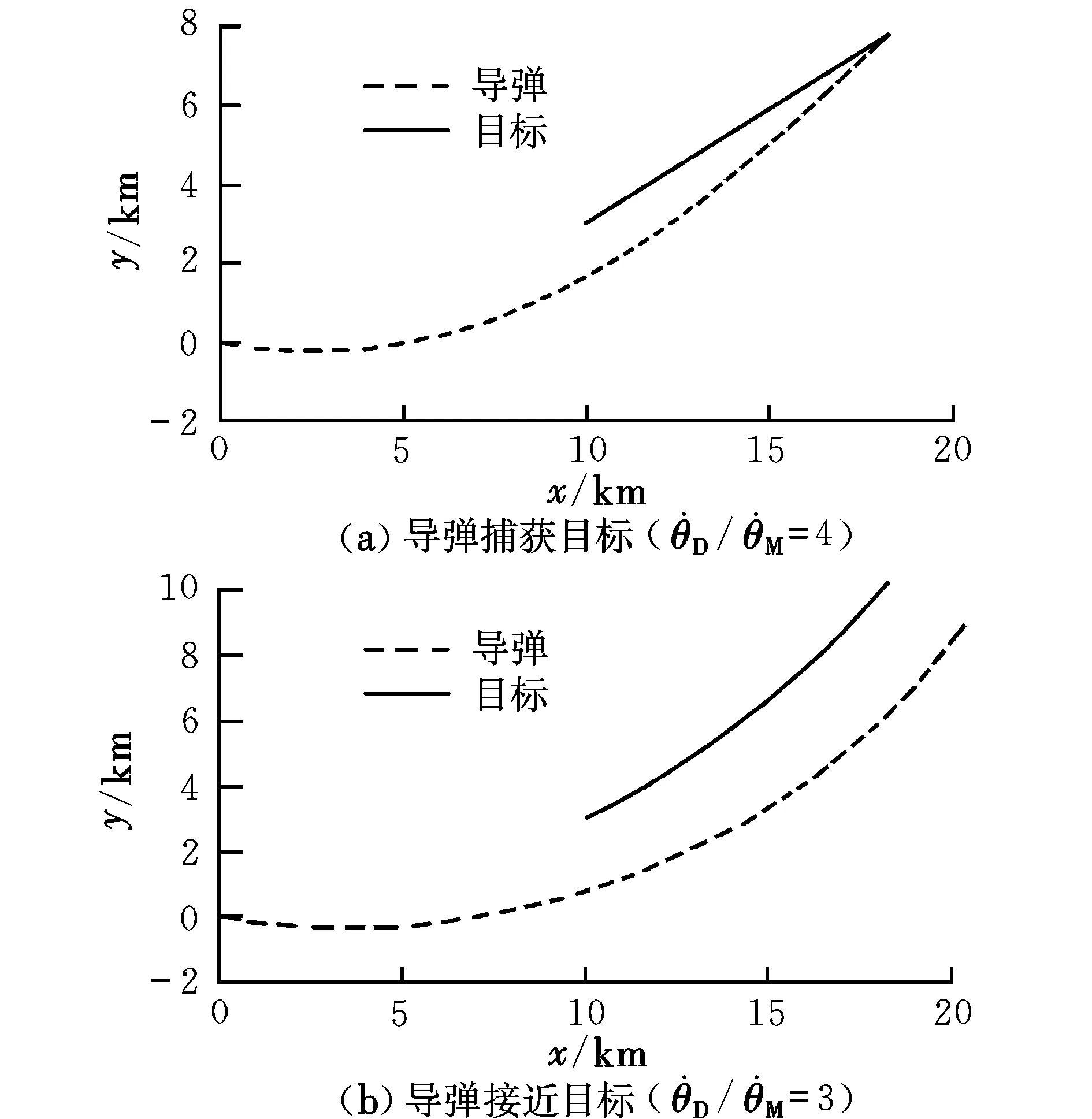
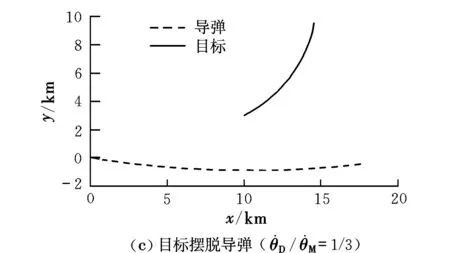
圖1 追逃問題的微分對策仿真結果1Fig.1 The first differential game simulation results of the pursuit-evasion resistance
4.2 仿真示例2
在上述性能指標中減去控制能量約束,即:
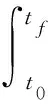
(13)
采用相同的設置,追逐方(導彈)的最大機動能力是逃避方(目標)的4倍、1倍、2/3和1/3,雙方軌跡如圖2所示。對策時間分別為73.42 s,54.92 s,40.62 s,31.43 s。
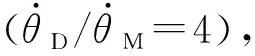
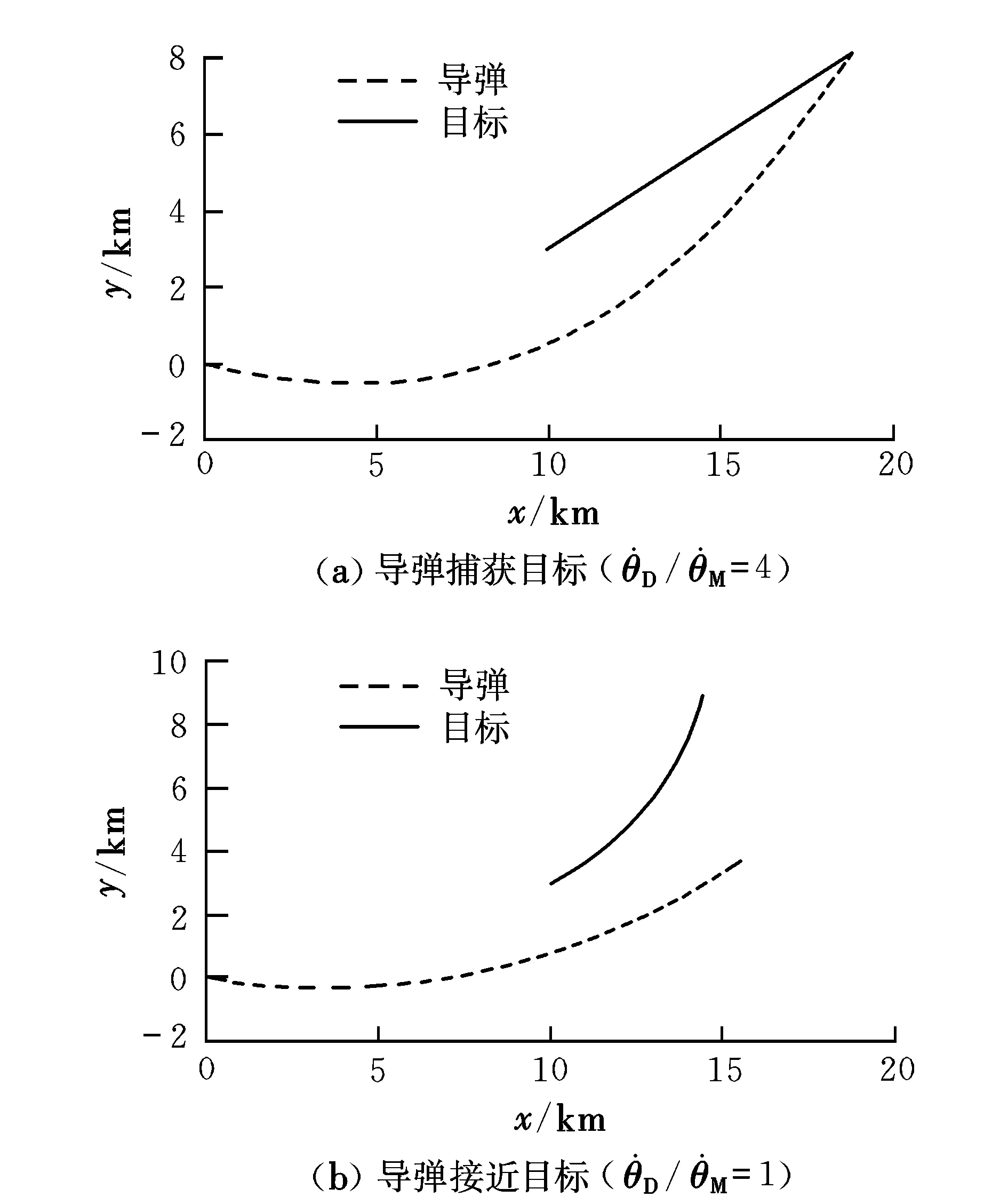
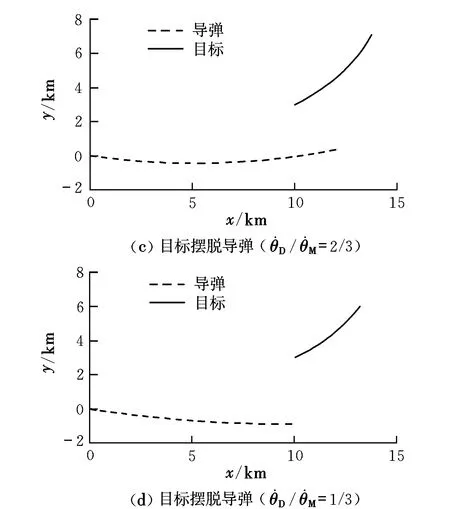
圖2 追逃問題的微分對策仿真結果2Fig.2 The second differential game results of pursuit-evasion resistance
5 結束語
本文建立了縱向平面內空戰雙方追逃對抗的微分對策數學模型,采用極小值原理和梯度迭代法對飛機-導彈縱向平面內的追逃問題進行了數值仿真,得到了雙方不同機動能力下的追逃仿真結果。從仿真結果可以看出,追逃雙方均以最大機動能力機動,當雙方最大機動能力之比不同時,得到捕獲、接近或擺脫幾種對策結果。微分對策中,當tf自由時,其迭代計算耗時遠大于tf固定的情況,難以在空戰中應用以實時在線生成航跡,因此在實時空戰仿真中,可將整個對抗過程分為若干段,在每一時間段內進行微分對策,即可滿足實時在線航跡生成的要求。本文的研究成果可用于防空導彈作戰效能評估、一對一空戰對抗雙方的最優決策研究。
參考文獻:
[1] Tahk Min-Jea,Ryu Hyeok,Kim Je-Gyum.An iterative numerical method for a class of quantitative pursuit-evasion games[R].AIAA-98-4118,1998.
[2] Basar T,Olsder G J.Dynamic noncooperative game theory[M].New York:Academic Press,1995.
[3] 湯善同.微分對策制導規律與改進的比例導引制導規律性能比較[J].宇航學報,2002,23(6):38-42.
[4] 羅生,宋龍.微分對策制導[J].航空科學技術,2011,(3):68-70.
[5] 梅丹,吳文海,徐家義.現代戰機空戰對策模型研究[J].飛機設計,2007,27(2):69-73.
[6] 王發坤,秦艷琳.三維空間中追逃對抗定性微分對策模型研究[J].船舶電子工程,2008,28(7):8-10,175.
[7] 黃力偉.求解微分對策問題的混合法[J].火力與指揮控制, 2011,36(1):50-52.
[8] 泮斌峰,唐碩.吸氣式空天飛行器閉環上升制導研究[J].飛行力學,2010,28(6):48-51.

