航天器共振軌道特性研究

史格非, 方群

(西北工業大學 航天飛行動力學技術國家重點實驗室, 陜西 西安 710072)

0 引言

在空間機動過程中,發動機推力大小有限,推進并非瞬間完成,特別是對于容許過載比較小的航天器進行軌道機動時,沖量假設不再成立,必須研究連續推力軌道機動。對于連續推力機動軌道的描述有很多[1],本文所研究的共振軌道就是一種新型的連續推力軌道。

共振是自然界的一種普遍現象,航天器在連續推力作用下的運動在參數平面內可以視為一種受迫振動,也會發生共振現象。因此,可以利用共振原理來研究航天器的運動,稱這樣一類非開普勒軌道為共振軌道(值得注意的是,這里的共振軌道與天體力學中定義的共振軌道有本質的不同[2])。航天器的共振軌道實質上是一種建立在新型坐標系下的非開普勒軌道,它是一種可以應用于軌道機動的過渡軌道。航天器共振軌道理論提出時間不長,國內外在這方面的研究還很少。

本文是在文獻[3]提出的共振軌道理論的基礎上深入研究共振軌道的軌道特性。通過對共振軌道在典型任務中的應用與傳統軌道機動模式進行仿真對比分析,闡述了單段共振軌道在航天器軌道機動中應用的優勢與不足。

1 航天器共振軌道模型的建立

1.1 共振軌道模型

航天器在平方反比中心引力和推力作用下的平面運動方程為:

(1)

引入新的時間尺度s(廣義偏近點角),它和物理時間t的關系為[3]:

(2)

式中,E為航天器單位質量具有能量的負數。

由Levi-Civita變換[4]可得:

r=L(u)u

(3)

在此基礎上引入準推力加速度[3]:

q=Mp

(4)

準推力可以視為對推力進行坐標變換的一種推廣。準推力與航天器質量的比稱為準推力加速度。其中:

(5)

利用式(2)～式(4)可以將式(1)轉化為線性方程:

該方程即為平面Y-C方程[3]。

假設準推力加速度為簡諧激勵,即準推力加速度具有如下形式:

(6)

式中,A1,A2為幅值;ω為準推力加速度的角頻率;φ1,φ2為初始相位。令:

(7)

則式(6)可以寫為:

q(s)=acos(ωs)+bsin(ωs)

(8)

將式(8)代入平面Y-C方程(ω=1/2),解得平面共振軌道的軌道方程為:

(9)

1.2 物理坐標系與參數坐標系的相互轉換

物理坐標系即地心坐標系,其參數為通常使用的位置、速度矢量。參數坐標系是一個通過對物理坐標系參數進行L-C變換而得到的新的坐標系,其參數皆為無量綱參數。

文獻[3]中的L-C變換為數學上的變換,沒有考慮計算機仿真應用。為了便于計算機仿真,避免仿真過程中會因出現奇異點而引起仿真失敗,本文將物理平面與參數平面上的點用參數的形式表示:

x=rcosθ,y=rsinθ

根據L-C變換的定義并結合幾何意義,可以得到一個物理平面上的點所對應的兩個參數平面上的點:

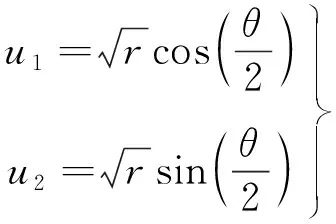
(10)

在得到物理-參數坐標的轉換后即可以利用L-C速度轉換式[4]:

(11)

得到對應點處的速度矢量。

1.3 參數描述

由于共振軌道模型是建立在參數坐標系下的,因此應用共振軌道時始終存在軌道參數在參數坐標系和物理坐標系之間的轉化。物理坐標系下的位置矢量可以表示為:

(12)

將式(9)代入上式,可以得到x和y關于s的表達式,帶入式(11)可以得到速度矢量關于s的表達式。從而得到以廣義偏近點角s為自變量的軌道與速度(x(s),y(s),vx(s),vy(s))方程。

2 利用共振軌道進行軌道機動的仿真分析

2.1 仿真模型的建立

將能量的表達式改寫為:

(13)

利用式(5)和式(13)可以求出任意s值所對應的M和E。由式(8)則可以得到任意s下的準推力矢量。利用式(2)和式(4)可以將參數坐標系下的時間尺度(廣義偏近點角)和準推力轉化為其在物理平面上所對應的時間和推力。利用式(12)即可得到物理坐標系下任意時刻的位置矢量。利用式(11)可以得到物理坐標系下任意時刻的速度矢量。

2.2 仿真算例

2.2.1 仿真條件

航天器的初始運行軌道為8 000～16 000 km的橢圓軌道;目標軌道為7 000～21 000 km的橢圓軌道;目標軌道相對于航天器初始運行軌道的拱線間夾角為25°(逆時針)。

通過單段共振軌道將初始軌道上的航天器機動到目標軌道上從而實現變軌。由于無法確定最省燃料的軌道初始位置和到達位置,因而采用窮舉法對初、末位置和時間尺度(廣義偏近點角)進行篩選和分析。將航天器初始運行軌道和目標軌道分別等分為36份從而得到36×36組出發/到達點,對每一組出發/到達點之間轉移所經過的s進行窮舉和篩選,得到每一組點的最佳時間尺度。在得到每一組的最優轉移軌道后,對36×36條軌道進行橫向比較,選出最省燃料的軌道并進行分析。

2.2.2 仿真結果及分析

仿真得到的燃料最省機動軌道參數結果為:航天器出發位置(x0,y0)=(6 509,5 462)km,航天器變軌到達位置(xf,yf)=(-14 005,-14 005) km,變軌速度增量ΔV=989.212 1 m/s,變軌飛行時間Δt=11 195 s,參數時間尺度sf=3.752 rad。航天器初始、目標及機動軌道如圖1所示。

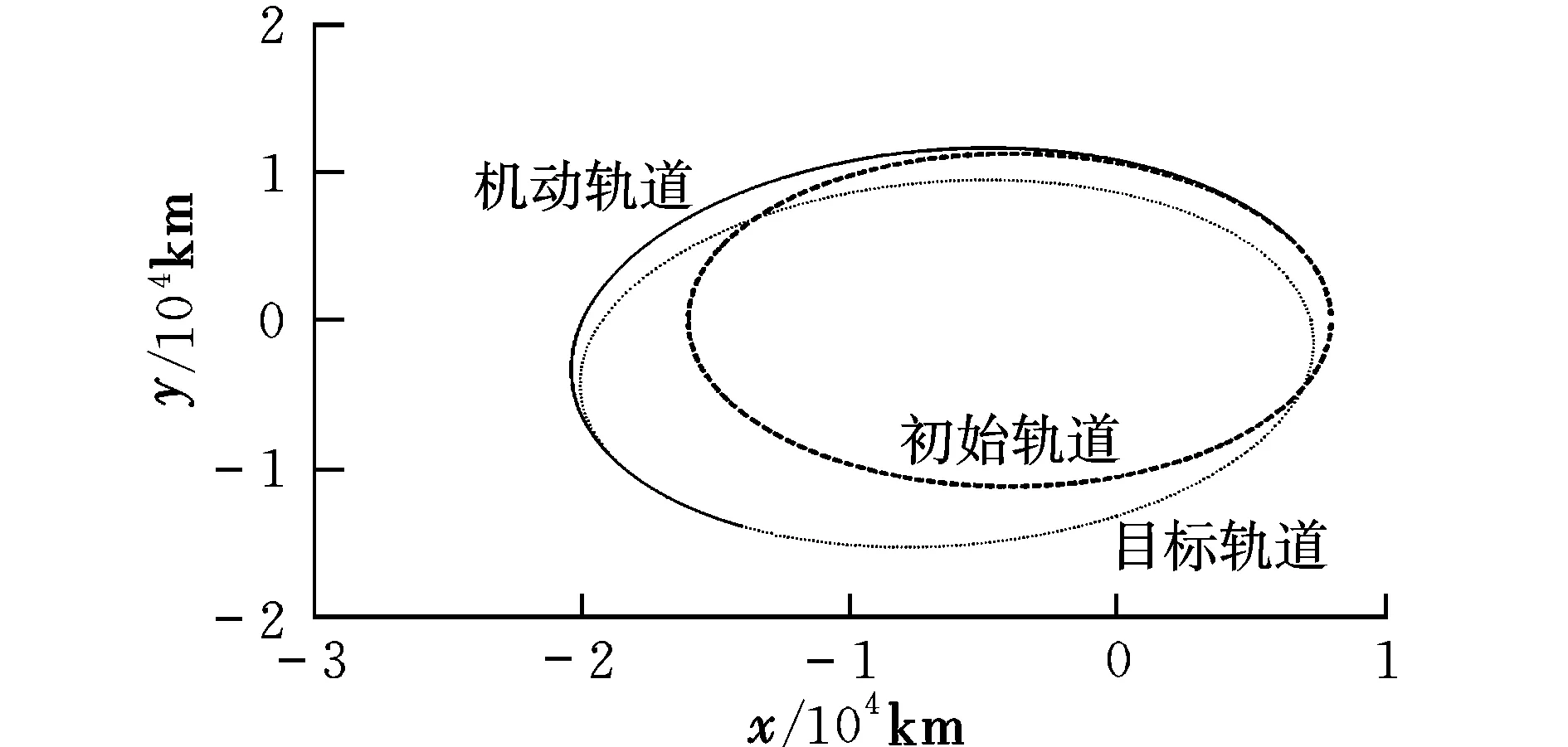
圖1 共振機動軌道示意圖Fig.1 Resonance transfer orbit

在本文的算例中,采用傳統的軌道機動策略,即在兩條軌道交點處通過施加脈沖進行變軌所需的速度增量為1 504 m/s[5],而利用共振軌道進行機動變軌所需的速度增量為989.211 2 m/s,這個數值大約為傳統單脈沖法的2/3。可見相比于單脈沖的軌道轉移方法,共振機動軌道是節省燃料的。因而在不考慮機動時間約束的情況下,利用共振機動軌道進行有交點軌道的變軌要優于單脈沖變軌。

本算例的推力曲線如圖2所示。由圖2可以看出,在整個機動飛行階段,推力峰值沒有超過0.35 N,即任意時刻的速度增量均在0.05～0.35 N之間,遠小于應用Lambert轉移時所需的最小速度增量(最小脈沖),這意味著應用共振軌道進行軌道機動的航天器不必使用大推力火箭發動機,即可產生的推力大小不再成為一種主要限制。

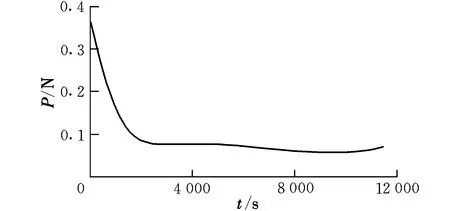
圖2 共振軌道推力曲線Fig.2 Resonance orbit thrust curve

在消耗相同時間的情況下,利用雙脈沖,通過Lambert轉移進行變軌得到的結果為:轉移時間Δt=11 195 s;第一次脈沖的速度增量ΔV1=659.7 m/s;第二次脈沖的速度增量ΔV2=222.6 m/s,總的速度增量ΔV=882.3 m/s。

將共振機動軌道與Lambert軌道進行對比可見,在時間相同的條件下,應用共振機動軌道進行變軌所消耗的燃料要略多于Lambert軌道。

3 共振軌道周期性和時間尺度分析

3.1 共振軌道周期特性分析

由共振軌道方程式(8)可知,在無推力的情況下，共振軌道是一種周期軌道。在有推力的情況下(以上文的算例為例),盡管共振軌道不是周期軌道,但也呈現出一種準周期性質。圖3表示對于同一組初始和到達參數,等效速度增量隨參數時間尺度變化量sf(廣義偏近點角改變量)的改變而發生的變化。這種變化帶有明顯的周期性。通過分析軌道參數與等效速度增量可知,等效速度增量的下峰值隨廣義偏近點角sf變化量的變化而有規律的出現,大約每4π rad出現一次。

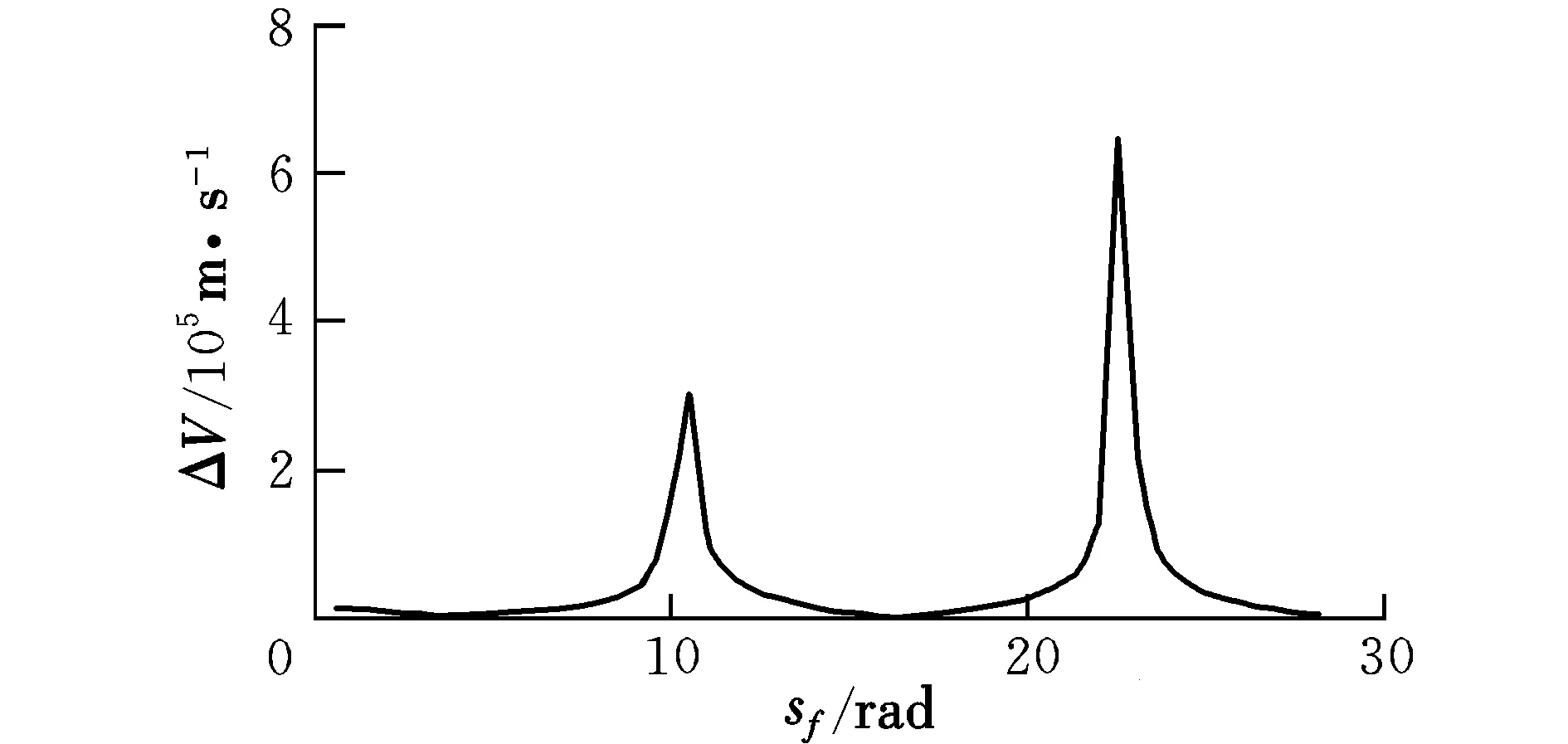
圖3 等效速度增量隨sf的變化曲線Fig.3 Changing of equivalent velocity with sf

由物理學知識可知:物體振動周期為2π/f。由于本文所建立的共振軌道方程其頻率為0.5,因此在理論上,共振軌道周期應該為4π。可見下峰值周期的出現是符合共振軌道的物理性質的。

3.2 共振軌道參數時間尺度特性分析

對于推力為0的共振軌道方程,共振軌道形式的線性開普勒軌道方程為:

(14)

在開普勒共振軌道方程下,s即對應為物理平面內航天器的偏近點角。在非開普勒軌道方程下,根據式(10),由于推力不再為0,因此a1,b1,a2,b2不再都等于0。共振軌道不再是式(12)所表示的簡諧振動軌道,sf與Δθ的嚴格對應關系也不再存在。

圖4中的曲線表示2.2節的仿真算例中，各組出發和到達參數所對應的最小等效速度增量所對應的sf值與物理平面內航天器所轉過的實際偏近點角的比值。圖中，橫坐標n為仿真結果序號。

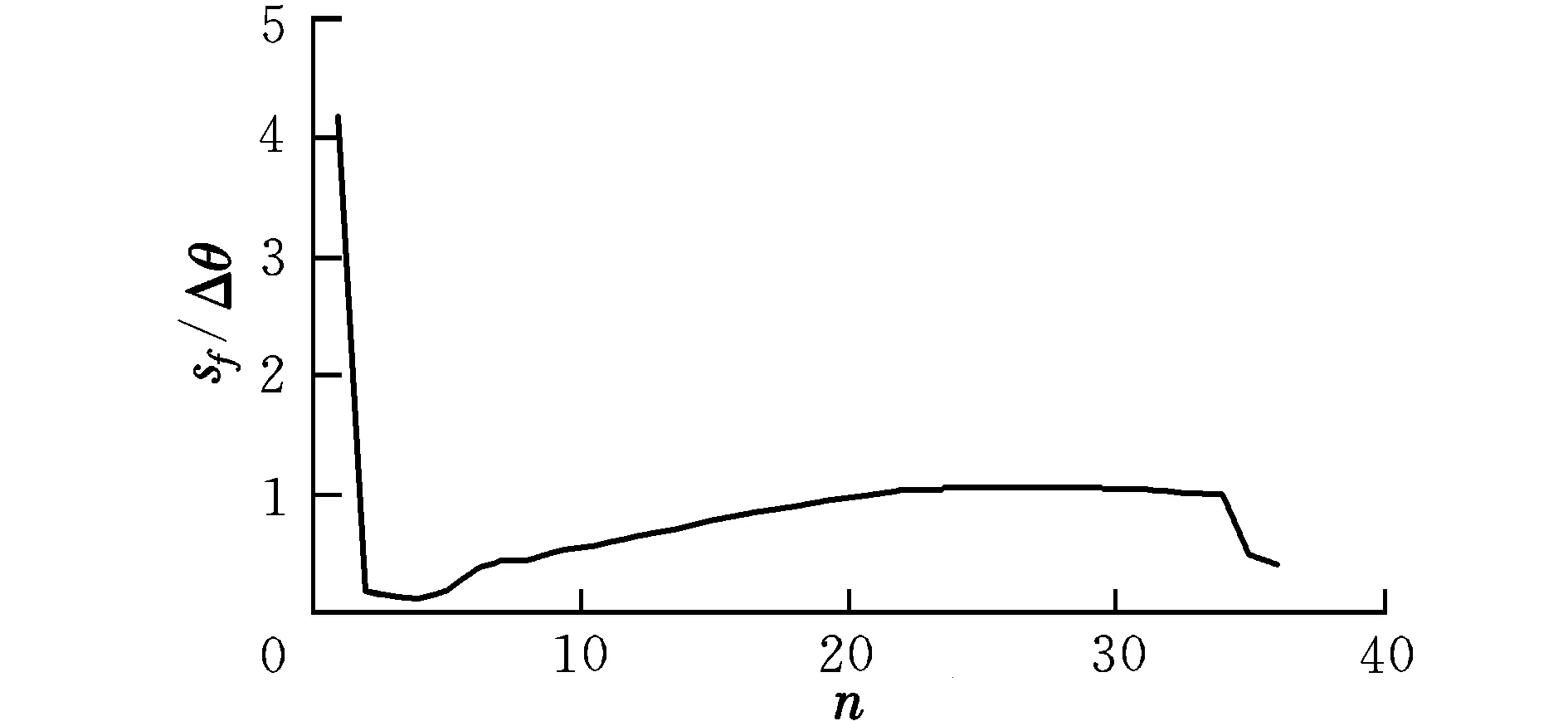
圖4 sf/Δθ曲線Fig.4 sf/Δθ curve

由圖4可知,sf/Δθ≠1,這說明在由式(9)所描述的有推力共振軌道中,廣義偏近點角s的變化量與物理平面上的偏近點角改變量沒有固定的對應關系。這意味著對于有推力的共振軌道,無法通過研究物理平面偏近點角的改變量來得到任務所需的最佳廣義偏近點角改變量sf。因此對最適合的航天器始軌道變軌和目標軌道到達點以及相應的sf的選擇目前只能應用窮舉法來實現。

4 結束語

本文針對頻率為0.5的典型共振軌道,從模型和參數描述以及轉換等方面進行了分析和補充,提出了共振軌道物理平面方程的直接參數描述方法。通過對共振軌道在典型任務中的應用與傳統軌道機動模式進行仿真對比分析,闡述了單段共振軌道在航天器軌道機動中應用的優勢與不足。同時,通過仿真計算對共振軌道周期特性進行了研究。

研究結果表明，在不考慮飛行時間約束的情況下,應用單段共振軌道作為轉移軌道要比傳統轉移軌道更節省燃料;在時間相同的情況下,共振轉移軌道消耗的燃料比Lambert軌道略多,但對發動機的推力要求很低;對于共振軌道的周期特性,廣義偏近點角s的變化量與物理平面上的偏近點角改變量沒有固定的對應關系。

參考文獻：

[1] McInnes C R.Solar sail mission applications for non-Keplerian orbits [J].Acta Astronautica,1999,45(4):567-575.

[2] 萬曉生,黃天依.冥王星軌道運動中的共振[J].紫金山天文臺臺刊,2000,19(2):80-84.

[3] 陳記爭.航天器非開普勒軌道研究[D].西安:西北工業大學,2010.

[4] 易照華,孫義燧. 攝動理論[M].第一版.北京:北京科學出版社,1981:52-76.

[5] Howard D Curtis.軌道力學[M].第一版.周建華,徐波,馮全勝,譯.北京:科學出版社,2009:226-229.