理想狀態下的雙離合自動變速器升擋過程滑磨功分析
向永樂,楊翔宇,謝 明,吳張兵
(重慶理工大學車輛工程學院,重慶 400054)
雙離合自動變速器(dual clutch transmission,DCT)結合了自動變速器(automatic transmission,AT)和機械式自動變速器(automated mechanical transmission,AMT)在舒適性和經濟性方面的優勢,且傳動效率高,結構緊湊[1],同時消除了AMT在換擋過程中動力中斷的缺點,實現了動力性換擋[2]。因此,雙離合自動變速器具有廣闊的發展空間和應用前景。按冷卻介質可將其分為干式雙離合自動變速器和濕式雙離合自動變速器,前者是靠空氣冷卻而后者則是靠油液冷卻。在頻繁換擋過程中產生大量滑磨功以致摩擦片溫度過高甚至失效仍為當前一大難題。本文就其升擋過程中離合器C1與離合器C2所產生的滑磨功進行探討。
1 DCT結構及工作特點
圖1所示為雙中間軸式干式離合器1、2擋結構簡圖。該DCT系統有7個擋位,2個離合器C1,C2交替工作,其中離合器C1與1,3,5,7擋相連,離合器C2與2,4,6及倒擋相連。以1擋升2擋為例,升擋過程中,離合器C1逐漸分離,離合器C2逐漸結合,離合器C1與離合器C2有一段重疊工作時間,本文將其稱為重疊量。根據不同的控制策略其重疊量也不相同。為論述方便,本文統稱逐漸結合的離合器為結合離合器,逐漸脫開的離合器為脫開離合器。
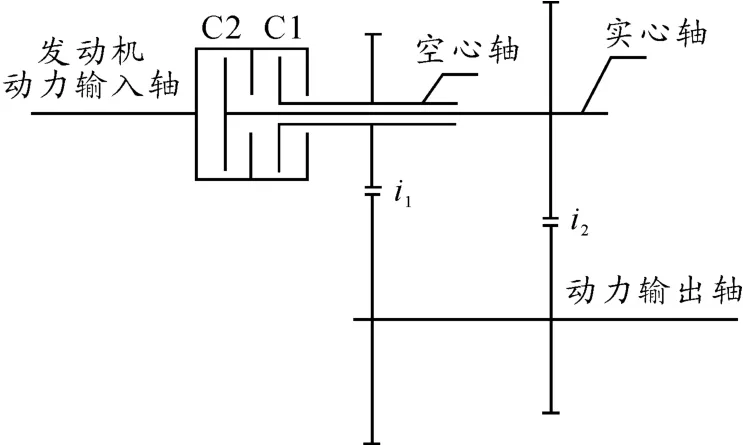
圖1 雙離合器1、2擋結構簡圖
2 控制策略的選定及所研究車型相關參數
不同的換擋控制策略決定了離合器的具體工作過程,在此以不同的重疊量制定3種典型控制策略進行分析探討。離合器C1所能傳遞的力矩TC1與離合器C2所能傳遞的力矩TC2隨時間t按如下3種控制策略變化(均以離合器C2開始結合為0時刻參考點)。

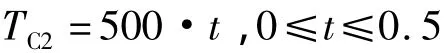
本文研究的車型有關參數如下:
1擋傳動比(i1):3.764;
2擋傳動比(i2):2.272;
驅動橋減速比(i0):4.437;
汽車總質量(W):1800 kg;
車輪滾動半徑(RT):45 cm;
離合器轉矩容量(Tmax):250 N·m。
為研究方便,本文作如下假設:
1)1擋升2擋發動機轉速變化很小,本文假定其恒
定不變,傳遞的力矩可在極限范圍內改變;
2)1、2擋車輛速度較低,忽略風阻的影響。
3 控制策略1
3.1 C1滑磨情況分析
根據滑磨功的計算公式可知,計算滑磨功須知道離合器主、從動盤轉速差和傳遞力矩的大小以及滑磨的時間。因此,準確地判斷離合器何時開始滑磨(本文將其稱為始滑點)與何時停止滑磨(本文將其稱為止滑點)至關重要。
在該種控制策略下離合器C1開始分離的同時,離合器C2就開始結合,C1在0.5 s完全分離,C2在0.5 s結合完畢。在離合器C1,C2重疊工作的過程中,C1與C2共同傳遞動力。由于離合器的轉矩容量遠遠大于車輛1擋行駛時離合器C1從動盤上的阻力矩,加之離合器C2的助力作用,離合器C1并非一開始分離就立即進入滑磨狀態。換言之,在1擋升2擋的過程中,存在這樣一個階段,即離合器C1已經開始分離卻尚未進入滑磨狀態,本文將該階段稱之為平衡態階段。
在平衡態階段,離合器C1所傳遞的力矩為靜摩擦力矩,大小由離合器C2所傳遞的力矩與道路阻力矩共同決定,并非與其當前所能傳遞的力矩相等。因此在平衡態階段有如下力矩平衡方程:

式(1)中:T'C1為離合器C1實際傳遞的力矩;TC2為離合器C2所能傳遞的力矩;MT1為1擋道路阻力矩,可用下式計算[3]:

式(2)中:W為汽車總質量;g為重力加速度;i0為驅動橋減速比;ik為k擋傳動比;φ為道路阻力系數,可用下式計算

式(3)中:f為滾動阻力系數,微型車、輕型車及轎車可取f=0.015;α為坡度角度。
由力矩平衡方程分析可知:當離合器C2單獨傳遞的力矩尚不足以克服當前阻力矩時,離合器C1與離合器C2共同克服阻力矩以維持車輛當前行駛狀態,車輛仍以1擋速度行駛。隨著TC2的增加,離合器C1實際所傳遞的力矩T'C1逐漸減小。與此同時,離合器C1所能傳遞的力矩TC1也在減小。將有關數據代入平衡方程可得:當t=0.024 s時,T'C1=0,TC1=238 N。由此可知:經過0.024 s離合器C2單獨所傳遞的力矩就已經足以平衡阻力矩,但此時離合器C1尚未完全分離,那么之后C1所傳遞的力矩將會變為阻力矩,會阻礙車輛加速,本文將其稱之為反拖。經計算,當t=0.321 s時=TC1,也就是說離合器C1在0.321 s才進入滑磨狀態,車輛的速度才開始改變,即t=0.321 s為C1的始滑點。那么在0.024~0.321 s內C1傳遞的力矩仍然為靜摩擦力矩,且為起阻礙作用的反拖力矩。當C1完全分離時,C1就停止滑磨,即 t=0.5 s為 C1的止滑點。在0.321~0.5 s內C1從動盤角速度為
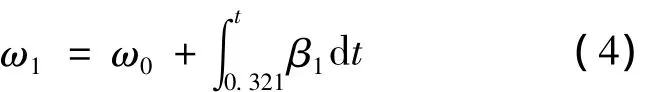
式(4)中:ω0為C1主動盤角速度;β1為C1從動盤角加速度,可由式(5)計算。
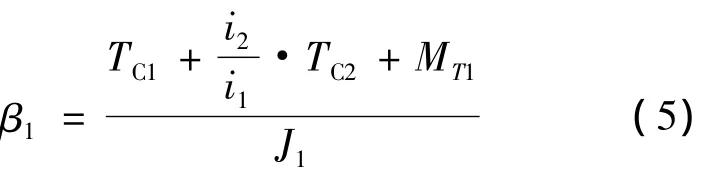
J1為汽車1擋當量慣量,J1可由式(6)計算。

在控制策略1下,離合器C1所產生的滑磨功(0.321 ≦ t≦ 0.5)為

該控制策略下力矩與滑磨功隨時間變化關系如圖2所示。
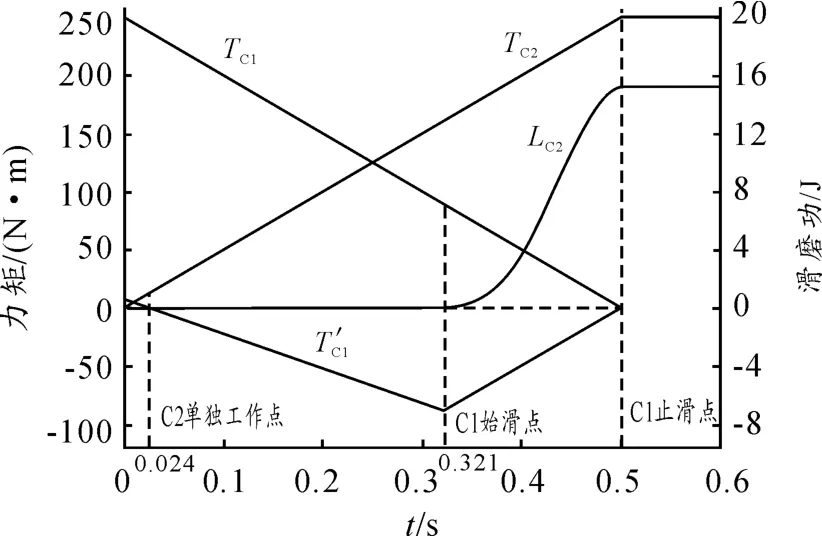
圖2 控制策略1力矩及C1滑磨功變化情況
3.2 C2滑磨情況分析
由于1擋傳動比i1大于2擋傳動比i2,離合器C2開始結合時其主、從動盤并不同速,則0時刻即為C2的始滑點。t=0.321 s時其從動盤才開始有角加速度,在0.321≤t≤0.5 s內 C2從動盤角速度為

式(8)中:ω20為離合器C2從動盤初速度;β2為C2從動盤角加速度,可由式(9)計算。

式(9)中:MT2為汽車2擋道路阻力矩;J2為汽車2擋當量慣量。
由此可算得t=0.5 s時,離合器C2主、從動盤仍未達到同速,也就是說離合器C2已經結合完畢后,C2還未停止滑磨。由此可見:0.5 s以后,C2從動盤仍會繼續加速;0.5 s到C2主、從動盤同速之前,其從動盤角速度為
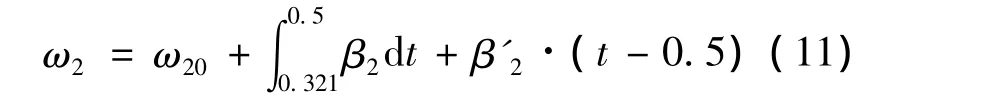
式(11)中β'2為C2從動盤0.5 s以后的角加速度,可由式(12)計算。
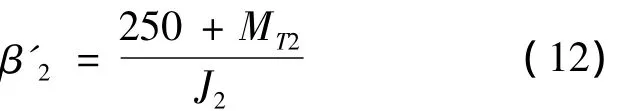
計算可得t=1.537 s為C2主、從動盤達到同速,即t=1.537 s為C2的止滑點。由以上分析可知:升擋過程中離合器C2的滑磨功須分3段分別計算,即
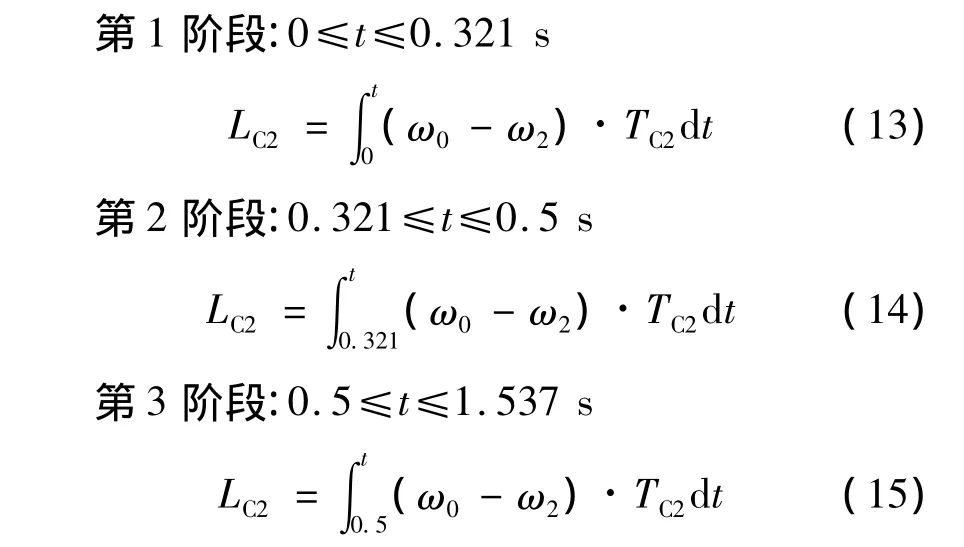
該控制策略下力矩與C2滑磨功隨時間變化關系如圖3所示。
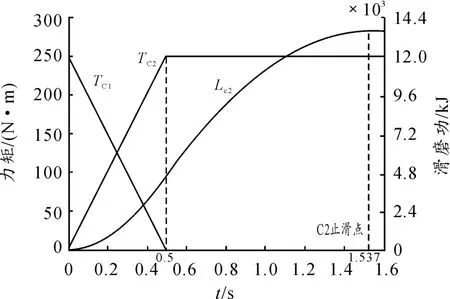
圖3 控制策略1力矩及C2滑磨功變化情況
4 控制策略2
與控制策略1的分析相同,在該種控制策略下,當離合器C2單獨傳遞的力矩足以克服阻力矩時,離合器C1恰好完全分離,那么離合器C1在整個換擋過程產生的滑磨功為0。離合器C2的始滑點為t=0 s,止滑點為t=1.388 s。滑磨功仍分3個階段來計算,升擋過程中總滑磨功為3段滑磨功之和,即
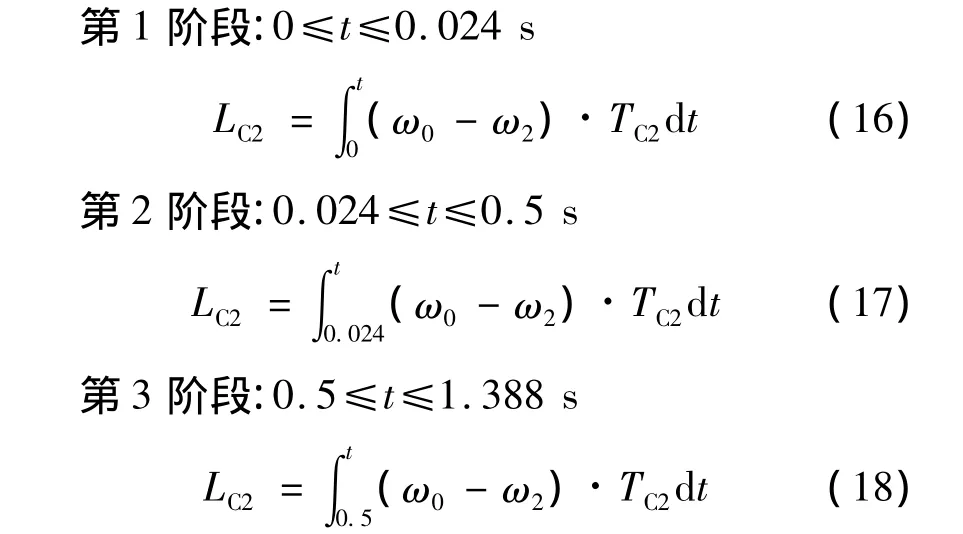
在該控制策略下力矩與滑磨功隨時間變化的情況如圖4所示。
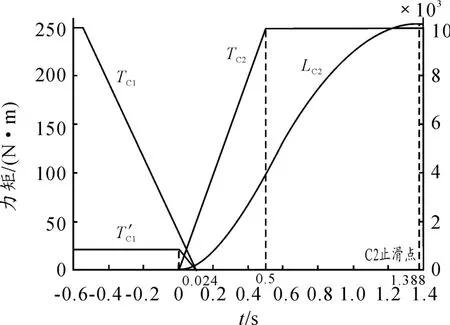
圖4 控制策略2力矩及C2滑磨功變化情況
5 控制策略3
由力矩平衡方程可算得該控制策略下,t=0.009 s時,TC1=T'C1。也就是說當離合器C2單獨傳遞的力矩還不足以克服阻力矩時,C1已進入滑磨狀態。在此情況下,換擋過程中車速會出現下降,將會出現動力不足。C1始滑點為t=0.009 s,止滑點為 t=0.018 s,所產生的滑磨功為(0.009 ≦t≦ 0.018)

該控制策略下力矩與C1滑磨功隨時間變化如圖5所示。

圖5 控制策略3力矩及C1滑磨功變化情況
C2的滑磨功須分為4個階段來計算,即
第1 階段:0≤t≤0.009 s

第2 階段:0.009≤t≤0.018 s
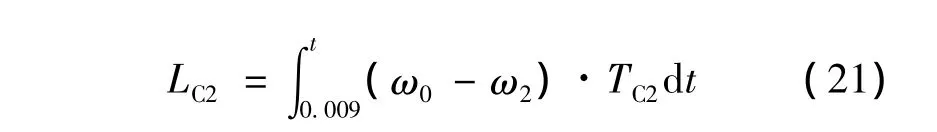
第3 階段:0.018≤t≤0.5 s
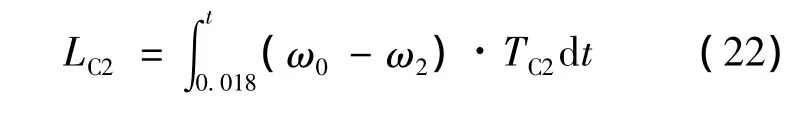
第4 階段:0.5≤t≤1.388 s

該控制策略下力矩與C2滑磨功隨時間變化的情況如圖6所示。

圖6 控制策略3力矩及C2滑磨功變化情況
6 結束語
雙離合自動變速器在升擋過程中,脫開離合器并非一開始減壓就立即進入滑磨狀態,其始滑點為其實際傳遞力矩等于當前可傳遞最大力矩時刻點。對于結合離合器,加壓結束并不代表其滑磨結束,其止滑點只能以主、從動盤同速確定。
由3種控制策略仿真結果的分析可知:C1與C2適當的重疊量,可使脫開離合器在整個升擋過程中滑磨功為0,同時結合離合器滑磨功最小,因此從滑磨功方面考慮該控制策略最優;過大的重疊量會使脫開離合器造成反拖,會延長升擋時間,造成結合離合器產生較大的滑磨功,對C1、C2均不利;過小的重疊量會造成換擋過程動力不足,影響動力的連續性,車速將有下降。無論采取何種控制策略,升擋過程中脫開離合器產生的滑磨功都遠遠小于結合離合器產生的滑磨功。
后續的研究中,可根據實際發動機的特性曲線來建立模型,以實現更精確的計算。
[1]Kulkarni M,Shim T,Zhang Yi.Shift dynamics and control of dual clutch transmission[J].Mechanism and Machine Theory,2007.42(2):168 -182.
[2]Goetz M,Levesley M,Corolla D,Integrated powertrain control of gearshifts on twin clutch transmissions[C]//SAE Paper,2004.
[3]汽車工程手冊.實驗篇[M].北京:人民交通出版社,2000:153-154.
[4]Goetz M,Levesley M C,Crolla D A I.Dynamics and control of gearshifts on twin clutch transmissions[J].Proceedings of the Institution of Mechanical Engineers,Part D(Journal of Automobile Engineer),2005,219(D8):951-963.
[5]Dovat F.The revolutionary VW-Audi double clutch transmission[C]//Internet Document.Ge Anlin & Others.Research on Dynamic 3-parameter Gear-Shift Schedule.SAE 912488,1991.
[6]KULKARNI M,SHIM T,ZHANG Y.Shift dynamics and control of dual-clutch transmissions[J].Mechani-sm and Machine Theory,2007,42(2):168 -182.
[7]ZHANG Y,CHEN X,ZHANG X,et al.Dynamic modeling and simulation of adual-clutch automated lays-haft transmission[J].Journal of Mechanical Design,2005,127(2):302-307.
[8]AMIR I A,QIN Datong,LIU Zhenjun.A control strategy on starting up of vehicle with automatic manual transmissions[J].Information Technology Journal,2005,4(2):140-145.
[9]Kulkarni M,Shim T,Yi Zhang.Shift dynamics and control of dual~clutch Transmission Mechanism and Machine Theory[M].2006.2.
[10]Steff Schnetzler,Joakim Petersson and Paavo MUrtonen.Quality Assurance of Driver Comfort for Automatic Transmissions[C]//SAE Paper.[s.n.],2000.
[11]Persson J.Intergrated powertrain control—a literature survey on longitudinal vibrations,drivability aspects and,future challenges[Z].Master Thesis EX024/2003,Control and Automation Laboratory,Department of Signals and Systems,Chalmers University of Sweden,March 2004.
[12]葛安林,車輛自動變速理論與設計[M].北京:機械工業出版社,1991.
[13]金倫,程秀生,葛安林,等.AMT換擋過程的離合器控制[J].汽車技術,2006(1):11-13.
[14]吳光強,楊偉斌,秦大同.雙離合器式自動變速器控制系統的關鍵技術[J].機械工程學報,2007,43(2):13-21.
[15]張哲誠.淺析雙離合器自動變速系統模型的建立[J].中國高新技術企業,2010,18:200-201.
[16]屠海峰.基于DCT結構的動力換擋過程研究[D].重慶:重慶理工大學,2010.
[17]李瑜婷,趙治國,章桐.DCT變速器雙離合器壓力最優控制方法的仿真研究[J].中國機械工程,2010,21(12):1496-1501.
[18]楊昭.雙離合器自動變速器動力學建模及仿真研究[D].長春:吉林大學,2007.

