基于微分進化的改進雜草優化算法

陶 玲，高曉智

(1.上海海事大學 信息工程學院，上海 201306;2.芬蘭阿爾托大學，赫爾辛基 00076)

入侵雜草優化算法［1］即Invasive Weed Optimization，在 2006 年由伊朗的 A.R.Mehrabian和 C.Lucas在Ecological Informatics雜志上發表的一篇論文中首次提出。它是一種模擬自然界雜草繁殖過程的隨機搜索方法，包括雜草入侵的種子空間擴散、生長、繁殖和競爭等過程，具有很強的魯棒性和自適應性，且算法簡單，易于實現。到目前為止，該算法已成功應用于基因調控網絡中的模糊神經模型的知識提取［2］、文本特征選擇［3］、DNA計算編碼序列的設計［4］等眾多領域。

在標準的IWO算法中，隨著迭代次數的增加，雜草個體產生種子，種子個體以父代雜草為均值，正態分布于雜草周圍。正是由于這種擴散機制，使得個體之間不存在信息交換，導致迭代后期種群多樣性差，局部搜索能力降低。同時，在標準IWO中存在以適應度為基準的繁殖機制。盡管這種機制給予了適應度差的個體生存和繁殖的機會，但適應度小的個體相應產生的種子也少，最終很有可能被直接剔除。這樣隨著繁殖的繼續，就會丟失很多有用信息，使算法陷入局部最優。為此，2008年Zhang等［5］提出一種基于文化框架的IWO算法(CIWO)，引入信念空間提高算法的局部尋優能力，使算法的收斂速度加快;2009年，Hajimirsadeghi等［6］將IWO和 PSO兩種算法進行融合，將PSO中粒子的速度和位移公式引入到雜草繁殖的種子個體中，使種子個體像PSO中的粒子一樣擁有速度，然后再對種子進行正態分布擴散，避免了算法陷入局部最優;2010年，Zhang等［7］又提出了一種改進的 IWO算法(MIWO)，在雜草產生后代時引入交叉算子以改進算法性能;2012年，Chen等［8］提出了一種基于混沌序列的多種群雜草算法，引入混沌序列和多種群機制來避免算法早熟，提高算法收斂速度和尋優精度;2013年，Peng等［9］將遺傳算法中的交叉和變異操作加入到IWO算法中，改善了算法的全局優化性能，獲得了較好的效果。

本文提出的IWODE算法在父代雜草個體繁殖種子后，引入一個隨機數對種子個體進行改進，以提高種子個體的質量，然后對繁殖一代后的種群引入差分進化算法中的變異、交叉和選擇思想，增加種群多樣性，提高算法性能。采用9個benchmark函數進行實驗。實驗結果表明:IWODE算法是有效的，其收斂精度和穩定性均有較大提高。

1 IWO算法

IWO算法基本流程［10］包括以下5個步驟:

1)初始化種群。雜草個體隨機擴散在D維搜索空間，初始種群大小可根據實際問題具體確定。

2)生長繁殖。雜草個體根據其適應度產生種子，適應度大的產生種子多，適應度小的產生種子少。父代雜草個體產生種子數與其適應度成線性關系，如圖1所示。

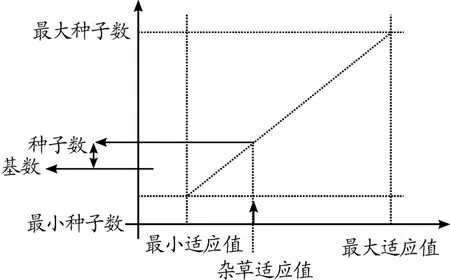
圖1 雜草產生種子的示意圖

3)空間擴散。子代個體以正態分布的方式擴散在D維空間中，以父代雜草為均值。每代擴散步長的計算如下:

其中，iter為當前迭代次數。

4)競爭排除。當繁殖數代后，種群規模超過環境的承受能力，則需要按照適應度進行淘汰，以達到種群上限要求。

5)重復步驟2)～4)，若達到最大迭代次數或最大種群規模，則結束循環，輸出最優解。

算法流程如圖2所示。

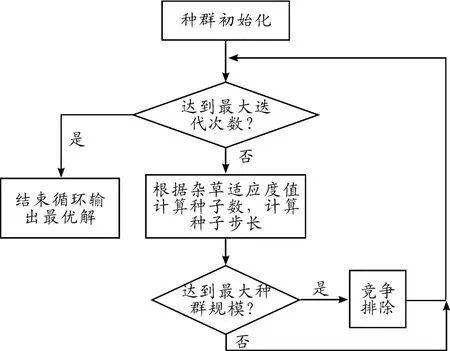
圖2 IWO算法流程

2 IWODE算法模型

IWODE算法流程如圖3所示。

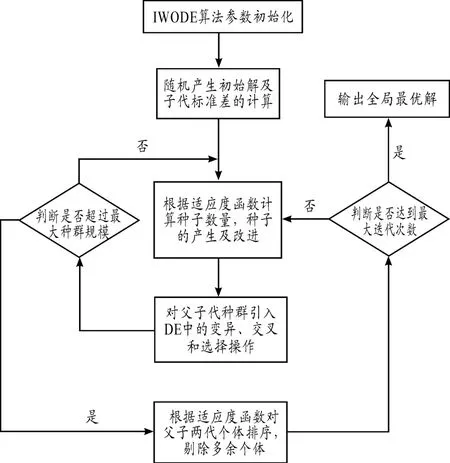
圖3 IWODE算法流程

2.1 對種子個體的改進

在解決連續性的工程問題時，種子個體采用正態分布的方式擴散在父代雜草周圍，這是雜草優化算法與其他優化算法的最大區別。由于本文求解的都是標準測試函數的極小值，所以在產生子代個體時，引入一個0～1之間的隨機數可以提高子代個體的質量，使得最終結果更加逼近最優解。種子個體正態分布計算見式(2)和(3)。

其中:delta_iter為標準差;X(i，:)為父代雜草個體。

2.2 對繁殖后的父子代種群的改進

在競爭排除前，對于繁殖了的種群，父代和子代個體一起，引入差分進化(DE)算法［11］中的變異操作，見式(4);隨機選擇待變異的個體，產生中間種群，然后對當代種群及其變異產生的中間種群進行個體間的交叉操作，見式(5);以一定的交叉概率判斷是否將中間種群的個體保留到下一代，最后對交叉后的種群進行選擇操作，見式(6);然后根據適應度值的大小判定要選擇的進入下一代的個體。

DE算法中的變異操作:

其中:i≠r1≠r2≠r3;G為壓縮因子;xi(g)表示第g代種群中第i個個體。

DE算法中的交叉操作:

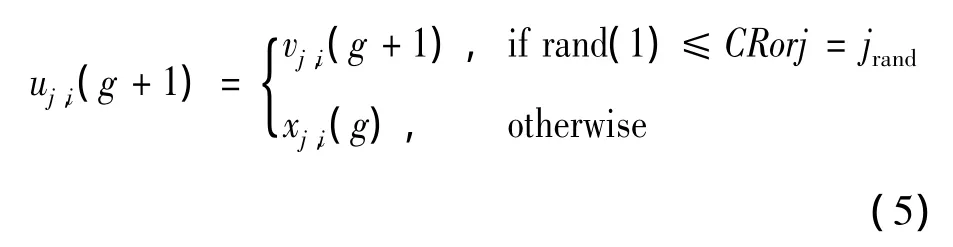
其中，CR為交叉概率 jrand∈［1，2，…，dim］的隨機整數。

DE算法中的選擇操作:

其中，f為測試函數。

2.3 IWODE算法復雜度分析

IWODE算法描述如下:

步驟1 產生初始種群個體數為M0個;

步驟2 根據適應度函數計算每個個體的適應度值，找到最大和最小適應度值;

步驟3 當iter=1，while iter＜=itmax;

步驟3.1 根據適應度值計算每個父代個體產生的種子數;

步驟3.2 根據式(1)計算每代種群正態分布的標準差;

步驟3.3 根據式(2)和(3)將種子個體正態分布于父代個體周圍;

步驟3.4 根據適應度函數計算每個種子個體的適應度值;

步驟3.5 將新的種子個體加入到父代種群中構成父子代種群;

步驟3.6 根據適應度函數計算父子代種群每個個體的適應度值;

步驟3.7 對于父子代種群中的每個個體:

當 it=1，while it＜ =100;

① 根據式(4)、(5)、(6)對個體引入DE中的3種操作;

② it=it+1，end while;

步驟3.8 對于新的種群:

if M＞Mmax;

①根據適應度值將新的種群個體排序;

②排除多余的個體直到M=Mmax;

步驟 3.9 iter=iter+1，end while;

步驟4 輸出最優解。

在IWODE算法中，最壞情況下的復雜度估計如下:

1)在步驟1中，時間復雜度，初始化M0個個體;

2)在步驟2中，計算每個個體的適應度值;

3)在步驟3.1中，計算每個父代個體產生的種子數;

4)在步驟3.2中，計算每代種群正態分布的標準差;

5)在步驟3.3中，種子個體正態分布于父代個體周圍;

6)在步驟3.4中，計算每個種子個體的適應度值;

7)在步驟3.6中，計算父子代種群每個個體的適應度值;

8)在步驟3.7中，引入DE操作，更新父子代種群。

以上是IWODE算法的復雜度估計，其他步驟中算法復雜度較低，可以忽略。

3 實驗結果與分析

3.1 實驗平臺

所有仿真實驗均在Windows 7操作系統，CPU為酷睿 i3－2375，主頻為1.50 GHz，內存為2 GB的計算機上完成，采用Matlab編程。

3.2 IWODE和IWO算法參數設置

兩種算法涉及到的所有參數設置見表1。分別對9個測試函數進行仿真，所有測試函數均獨立運行50次，每個函數每次迭代50代。

表1 算法參數設置

3.2.1 實驗結果

表2是本文采用的測試函數，其中:f1，f2，f3，f7，f8是單峰函數，f4，f5，f6，f9是多峰函數。

表3是IWODE與IWO獨立運行50次的測試結果比較。圖4～12是9個函數分別迭代1 000代的收斂曲線。

表2 benchmark函數

圖4 函數f1的收斂曲線

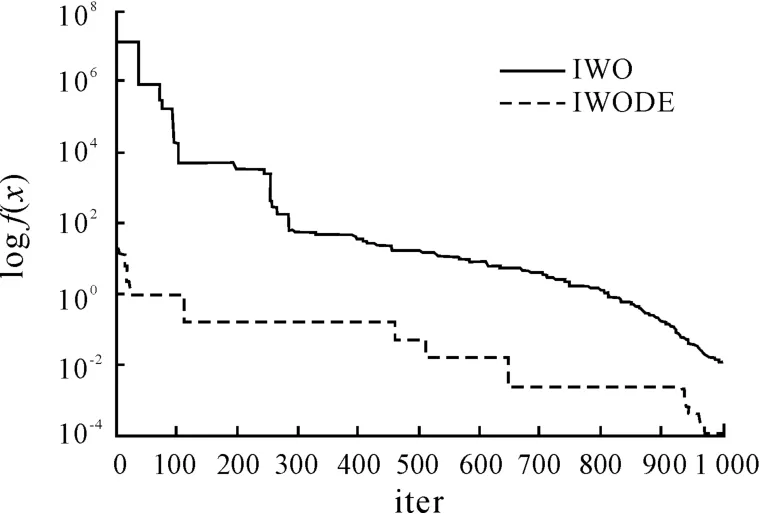
圖5 函數f2的收斂曲線

圖6 函數f3的收斂曲線

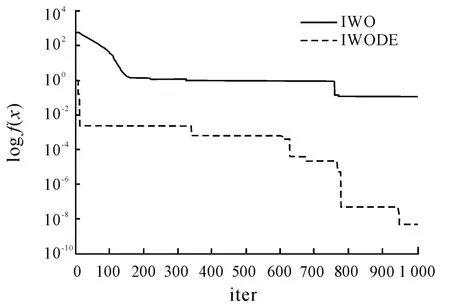
圖7 函數f4的收斂曲線

圖8 函數f5的收斂曲線

圖9 函數f6的收斂曲線

圖10 函數f7的收斂曲線

圖11 函數f8的收斂曲線

圖12 函數f9的收斂曲線

3.2.2 結果分析

從表3可以看出:IWODE的各項測試結果幾乎均優于 IWO。對于 f1，f2，f3，f5，f6，f7，f9，IWODE的最優值、最差值、平均值和標準差均遠優于IWO。IWODE完全找到了相應測試函數的全局最優解，它的尋優精度和穩定性相比IWO要高很多。對于f4，IWODE的最優值、最差值、平均值和標準差相比IWO分別高15，8，10，9個數量級。對于f8，雖然IWODE的最優值次于IWO，但IWODE的最差值、平均值和標準差都比IWO好。以上結果表明:IWODE算法可行有效，且有較高的尋優精度和穩定性。

圖4～12是9個函數分別迭代1 000代的測試函數收斂曲線。圖4，5，6，10，11 分別是 f1，f2，f3，f7和 f8這 5 個單峰函數的收斂曲線，圖7，8，9，12分別是f4，f5，f6，f9這4個多峰函數的收斂曲線。從圖4～11可以看出:IWODE算法的收斂速度較IWO好，最后獲得的最優解優于IWO算法。而在圖12中，IWODE算法的收斂速度明顯快于IWO算法，且求得的最優解也優于IWO。以上結果表明:IWODE算法適合高維函數尋優，無論函數是單峰的還是多峰的。

3.3 IWODE和GA、PSO的比較

為進一步表明本文算法的有效性，將IWODE和GA、PSO進行比較，選擇函數f4進行測試。其中，函數獨立運行次數為50，維數為30，IWODE其余參數設置與表1相同。表4為仿真結果，表中的成功率定義為:n/50(n表示50次運行結果中最優解＜0.005的次數)。

表4 仿真結果

從表4可以看出:IWODE的尋優精度優于GA和PSO，IWODE的平均值分別優于GA和PSO 13，12個數量級，并且IWODE算法相比GA和PSO在迭代次數較少的情況下獲得了更好的結果。

4 結束語

本文針對基本IWO算法的不足，對產生的種子個體進行改進，以提高種子個體質量，從而提高算法的尋優精度，同時在父子代種群中引入差分進化算法中的各種思想，增加后期種群多樣性，改善了算法的全局尋優能力和算法的穩定性。本文還將IWODE與PSO和GA進行比較。從仿真結果可以看出:IWODE算法取得了較好的結果。

［1］MEHRABIAN A R，LUCAS C A.novel numerical optimization algorithm inspired from weed colonization［J］.Ecological Informatics，2006，1(4):355－366.

［2］PRATYUSHA RAKSHIT，PAPIA DAS，AMIT KONAR，et al.A recurrent fuzzy neural model of a gene regulatory network for knowledge extraction using invasive weed and artificial bee colony optimization algorithm［C］//1st Int’1 Conf.on Recent Advances in Information Technology|RAIT－2012|.Piscataway:IEEE，2012.

［3］劉逵.基于野草算法的文本特征選擇研究［D］.重慶:西南大學，2013.

［4］ZHANG XUNCAI，WANG YANFENG，CUI GUANGZHAO，et al.Application of a novel IWO to the design of encoding sequences for DNA computing［J］.Computers and Mathematics with Applications，2009，57(11/12):2001－2008.

［5］ZHANG XUNCAI，XU JIN，CUI GUANGZHAO，et al.Research on invasive weed optimization based on the cultural framework［C］//BICTA 2008:Proceedings of the 3rd International Conference on Bio-Inspired Computing:Theories and Applications.Piscataway:IEEE，2008:129－134.

［6］HAJIMIRSADEGHI H，LUCAS.A hybrid IWO/PSO algorithm for fast and global optimization［C］//IEEE EUROCON 2009.Piscataway:IEEE，2009:1964－1971.

［7］ZHANG XUNCAI，NIU YING，CUI GUANGZHAO，et al.A modified invasive weed optimization with crossover operation［C］//Proceedings of the 8th World Congress on Intelligent Control and Automation.Piscataway:IEEE，2010:11－14.

［8］陳歡，周永權，趙光偉.基于混沌序列的多種群入侵雜草算法［J］.計算機應用，2012，32(7):1958－1961.

［9］彭斌，胡常安，邵兵，等.求解TSP問題的混合雜草優化算法［J］.振動、測試與診斷，2013，33(z1):66－69.

［10］賈盼龍，田學民.基于自適應小生境的改進入侵性雜草優化算法［J］.上海電機學院學報，2012，15(4):225－230.

［11］楊啟文，蔡亮，薛云燦.差分進化算法綜述［J］.模式識別與人工智能，2008，21(4):506－513.