基于模態能量分析的結構滯回能量估算方法
王 豐,孫建剛
(大連民族學院土木建筑工程學院,遼寧大連116605)
結構在地震中的運動反應是一個耗散能量的 過程,用結構在地震下的累積能量來分析和評估結構的抗震性能更具合理性。近年來基于能量的抗震設計理論和方法得到了一定的發展[1-3]。基于能量的抗震設計就是要使結構或構件的耗能能力大于地震作用下結構或構件的耗能需求。
目前,對能量設計方法的研究主要集中在兩個方面:能量反應譜研究和結構能量反應研究。對于能量反應譜,學者們提出了各種各樣的能量譜,并進行系統研究,如輸入能量譜(Amiri和Darzi[4];Benavent 等[5])、滯回能量譜(Danny 和Mario[6];公茂盛和謝禮立[7])、吸收能量譜(Chou和 Uang[8])、瞬時輸入能量譜(陳逵和劉哲鋒[9])等。對結構能量反應的研究方面包括:結構的能量如何計算;結構的能量反應與結構的其他地震反應之間存在什么樣的關系,如何綜合各種反應指標評判結構的抗震性能等等。目前這些問題的研究只處于理論探討和數值分析階段(陳逵和劉哲鋒[10];Wong 和 Liu[11];陸鐵堅和秦素娟[12]),很多研究只針對剪切型結構(經杰、葉列平和錢稼茹[13];胡冗冗和王亞勇[14])。
地震下結構的滯回耗能是評估結構及構件累積損傷程度的重要指標,通過能量譜來估算結構滯回能量簡單,且具有統計意義。目前,滯回能量反應譜的研究已經得到了一定的發展,建立能量譜與結構耗能之間的關系則是當前需解決的關鍵問題,文章正是針對此問題展開研究。
1 基本原理
1.1 能量關系方程
考慮一幢n層對稱結構,假設結構各樓層的水平恢復力特性為理想彈塑性,該結構在單向水平地震作用下的能量平衡方程為
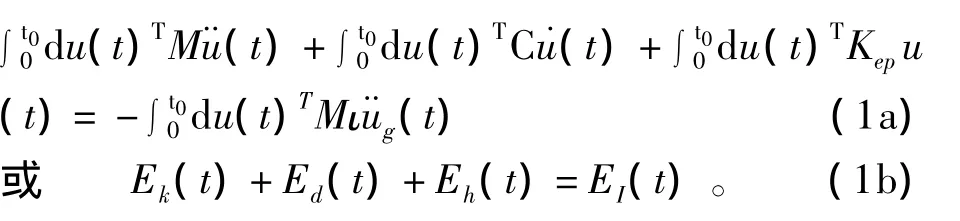
式(1a)中,u(t)為結構各層質心處的瞬時相對位移向量;F(t)為結構的恢復力向量,可表示為Kep(t)u(t),其中Kep(t)為系統的瞬時切線剛度陣;M和C分別為結構的質量矩陣和阻尼矩陣。式(1a)中的各項分別為結構的動能Ek、阻尼能Ed、滯回能Eh和相對輸入能EI。式(1b)為其簡化表達式。
將彈性模態分解的思路引入彈塑性分析中,假設彈塑性位移向量可以分解為
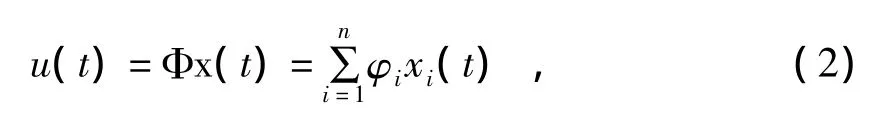
式中,Φ為振型矩陣,φi為第i階振型向量。將式(2)代入式(1a),有
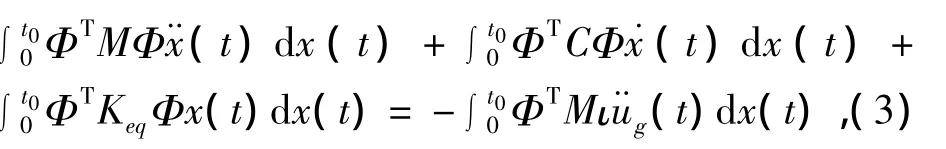
根據振型正交性,式(3)可以轉換為
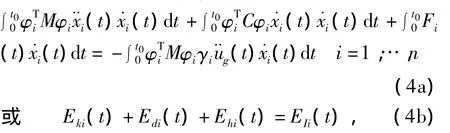
式中,Fi(t)= φiTKep(t)φixi(t);γi為第 i階振型參與系數。式(4a)可以看作結構的樓層側向位移按振型φi分布的虛擬振動反應狀態下的能量平衡方程。式(4a)中各項分別為動能Eki、阻尼能Edi、滯回能Ehi和輸入能EIi。式(4b)為其簡化表達式。式(4a)兩側同除以φTMφγ2,有iii
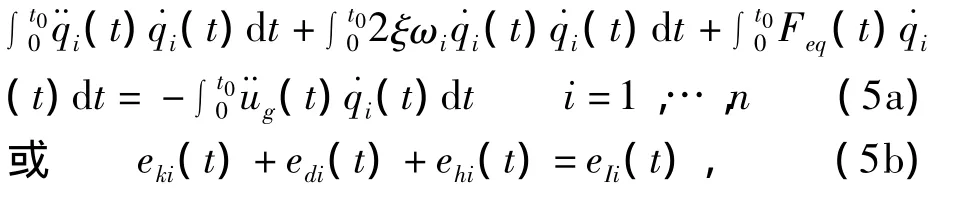
式(5a)中,qi(t)=xi(t)/ γi;Feq,i(t)= φiTKep(t)φiqi(t)。此式可以看作質量為1的各階模態等效單自由度(簡稱SDOF)體系在地震動作用下的能量平衡方程,式(5b)為其簡化表達式。
根據文獻[15]的推導,可以得到如下關系:
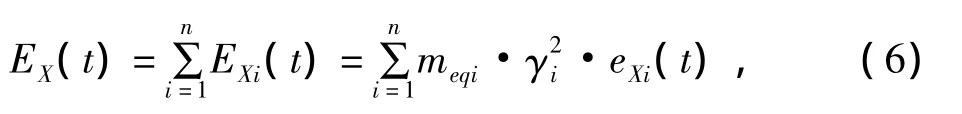
式中,meqi=φiTMφi;下標 X 分別表示 k、d、h 和 I,對應著四種能量項。
1.2 彈塑性模態振型假設
定義樓層位移反應不均勻系數為

其中,Δdij為按第i階振型模式的 Pushover得到的對應某基底剪力的第j樓層的層間位移,Δdmi為相應的n個樓層的平均層間位移。可以對結構按第i階振型模式進行Pushover分析,隨著推覆力的增大得到一系列的αi值,取αi最大值所對應的側向位移模式為φp,i。定義歸一化方法:n個樓層的絕對位移值(或樓層振型值)之和等于1。對彈性振型φi和側向位移模式φp,i進行歸一化處理。
由于傳統等效SDOF體系是基于振型不變的假設,然而在塑性反應階段結構的振型為瞬時振型。為使方法便于操作,在等效SDOF體系及能量轉換過程中,設第i階的彈塑性等效振型為

1.3 能量估算步驟
(1)將結構按各階模態等效為多個SDOF體系,通常取結構的前3~5階模態。計算各階模態等效SDOF體系的等效質量、等效阻尼。
(2)設各階模態等效SDOF體系的恢復力特性均為理想彈塑性。通過Pushover分析的方法得到結構基底剪力-頂層位移的能力曲線,然后簡化為雙線性形式,進一步可轉化為等效SDOF體系的力-位移關系。第i階模態推覆力分布模式為

(3)通過彈塑性滯回能量反應譜或者對等效SDOF體系輸入地震動的方法確定第i階模態等效SDOF體系的滯回能量值ehi(t),其中i=3~5。
(4)將ehi(t)代入式(6),計算結構總滯回能量。
2 算例分析
2.1 算例說明
考慮1幢6層建筑,針對《建筑抗震設計規范》給出的I、II、IV類場運用按振型分解反應譜方法設計樓層的抗剪強度,這樣相當于3座6層建筑。為了比較分析的方便,將算例建筑簡化為3個多自由度體系,建筑層高均設為3.6 m,側向剛度及屈服剪力系數沿樓層的分布均設計為均勻分布,樓層的力-位移模型采用雙線性理想彈塑性模型,阻尼采用Rayleigh阻尼,阻尼比取5%。樓層重量、振型、周期及樓層抗剪強度見表1。
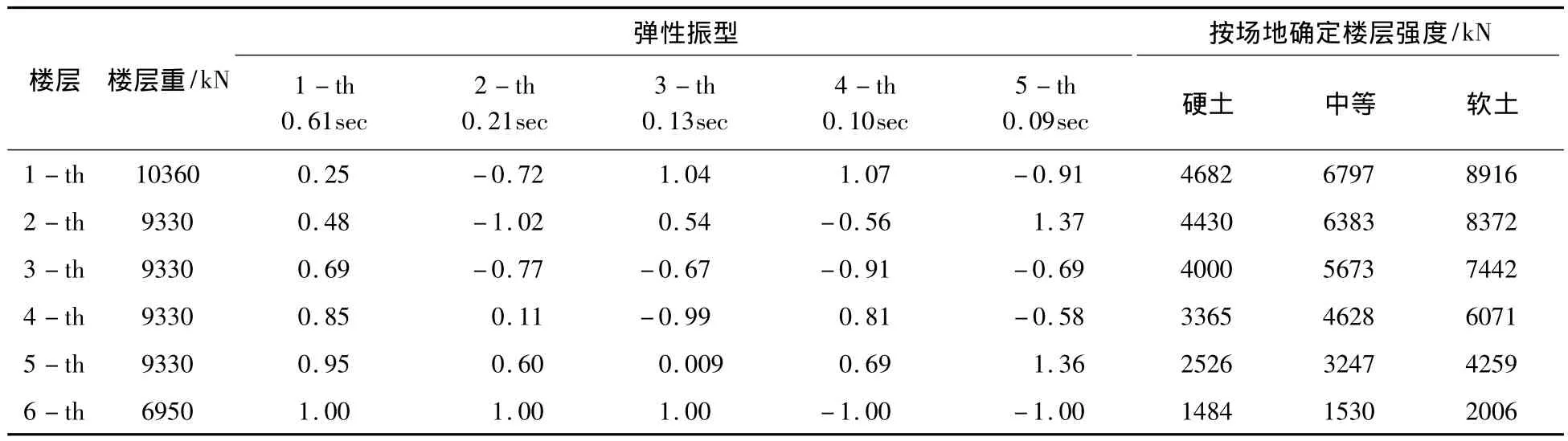
表1 算例結構基本信息表
2.2 地震記錄的選取
將場地條件分為硬土(I)、中硬(軟)土(Ⅱ)、軟土(Ⅳ)三類。每類場地選4條地震記錄,三類場地共12條,見表2。地震加速度峰值調整為4 m·s-2。
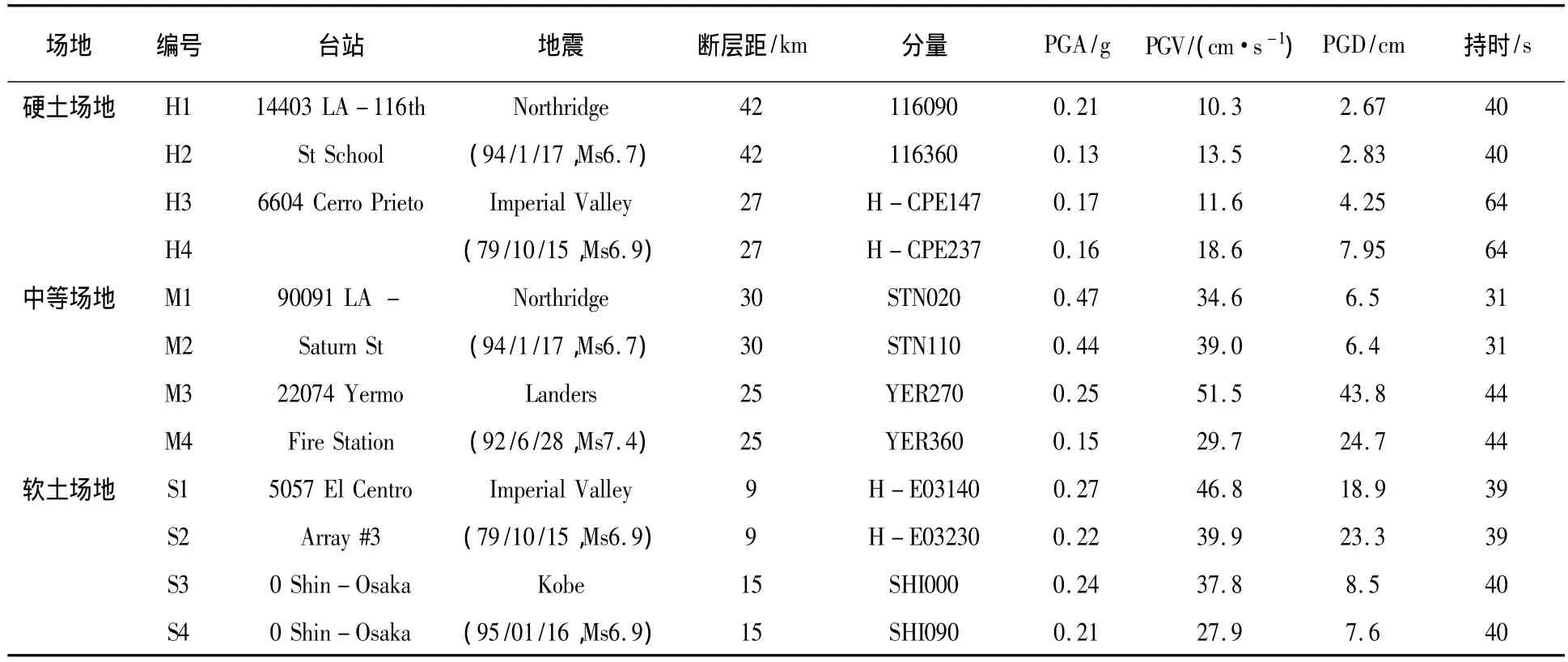
表2 地震記錄表
2.3 滯回能量估算分析
對算例工程分別采用非線性動力反應能量分析(簡稱NL-EA)法和模態能量反應分析(簡稱MEA)法,計算在選取地震動記錄作用下的結構整體滯回能量,并將兩種方法的結果進行比較分析。
分別運用NL-EA法和本文提出的模態能量分析(簡稱MEA)法計算得到結構總滯回能量值,見表3。其中NL-EA方法的結果可看作精確解,MEA方法的結果與精確解的偏差也列于表中。從表3可知,三類場地下MEA法估算滯回能量的平均偏差分別為9.4%、4.6%和12%。總平均偏差為8.7%,說明通過MEA方法得到的結構整體滯回能量時程在趨勢上與精確解符合較好。
分析偏差與各地震動特點可知:高振幅持時較長的地震動作為輸入時,能量估算偏差較大;相反,高振幅持時短或出現少數明顯的峰值加速度的地震動作為輸入時,估算偏差則較小。分析原因:地震作用下結構經過往返多次大位移變形后,它的整體恢復力關系(頂層位移-基底剪力)與其等效SDOF體系的恢復力關系的差異會逐漸增大,基于模態的能量估算偏差自然也會很大;相反,只經歷少數幾次大的變形則偏差會較小。

表3 結構整體滯回能量表
采用MEA方法和NL-EA方法得到的結構整體滯回能量時程如圖1-圖3。從圖中可以看到,基于MEA方法與NL-EA方法的滯回能時程在趨勢上符合較好。對于能量偏差較大的情況,通常在時程開始階段偏差較小,隨著持時增加結構耗能逐漸增大,偏差也逐漸增加。分析原因:MEA方法是基于模態等效SDOF體系假設,而等效SDOF體系分析適用于塑性反應較小時,當塑性反應增大,特別是往復塑性反應增大,其準確度也相應降低。
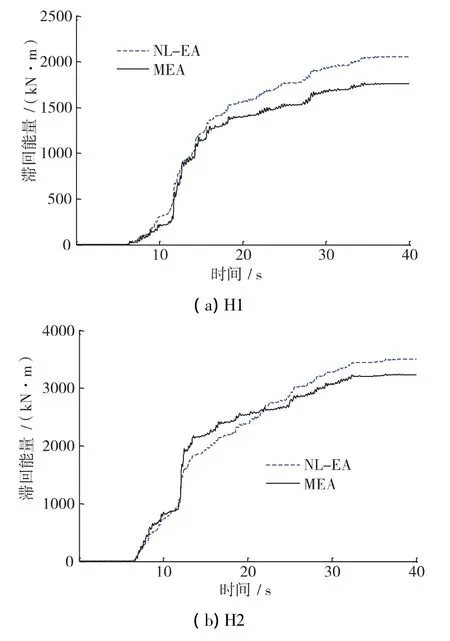
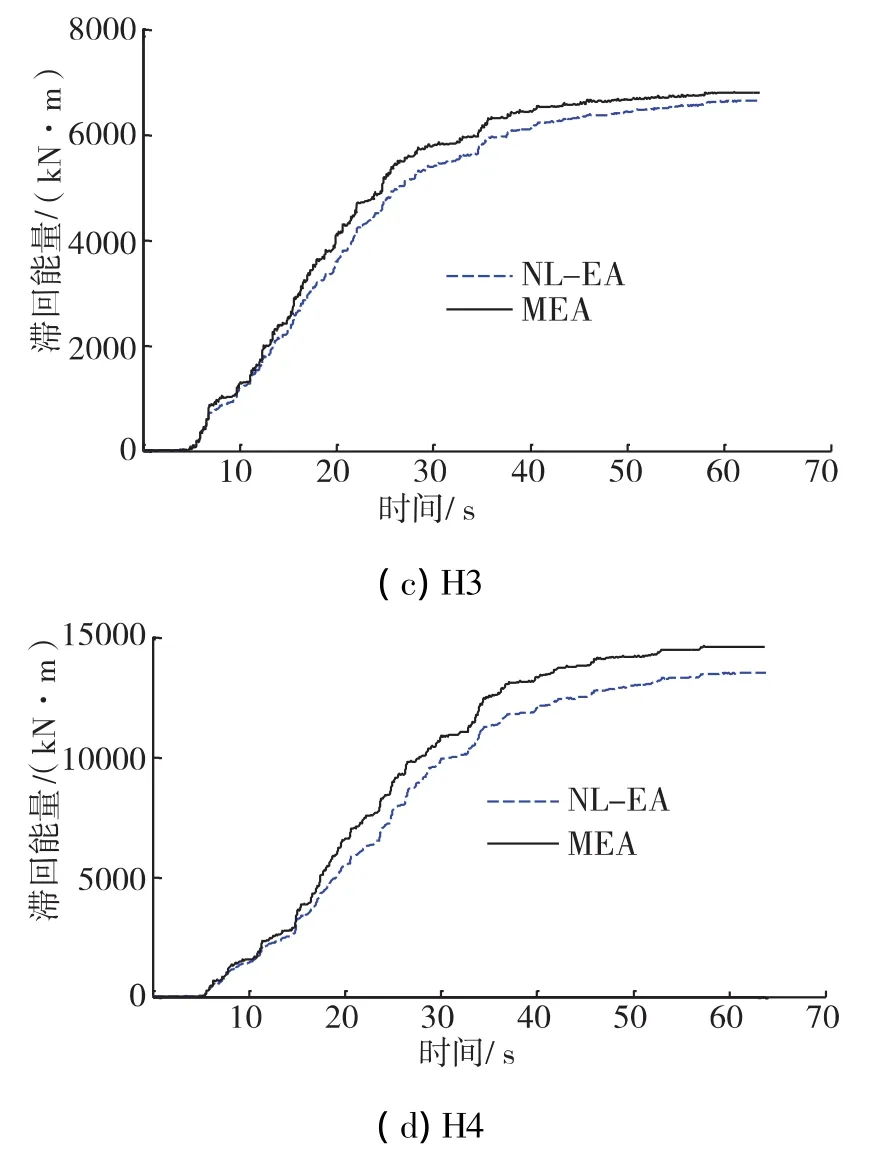
圖1 硬土場地下通過MEA法和NL-EA法計算得到的滯回能量時程比較
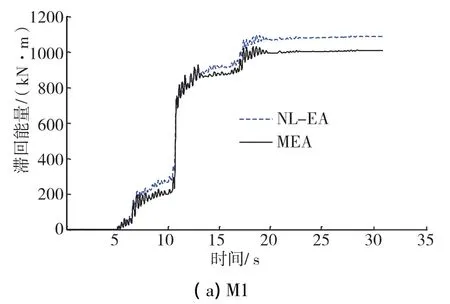
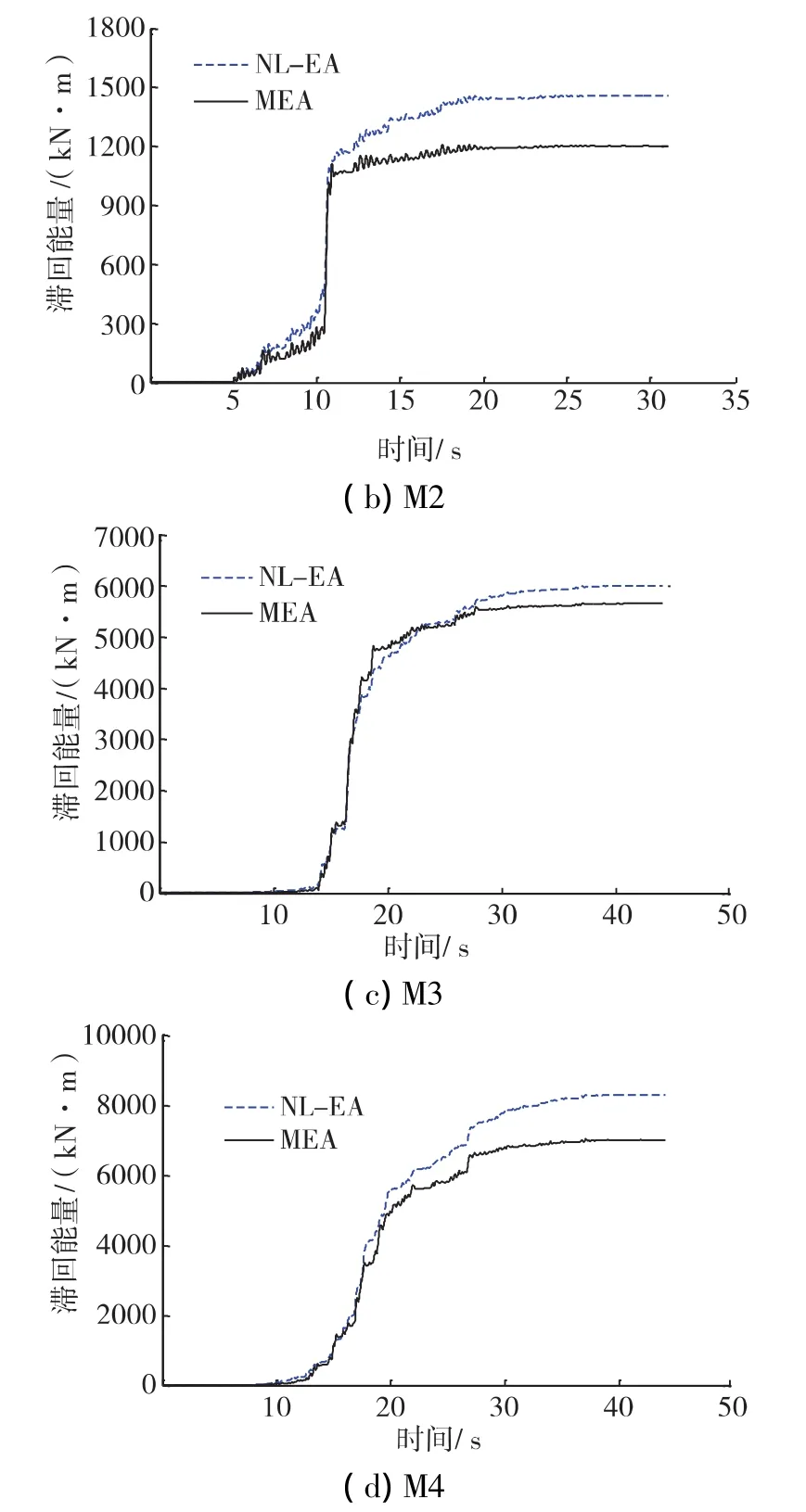
圖2 中硬(軟)土場地下通過MEA法和NL-EA法計算得到的滯回能量時程比較
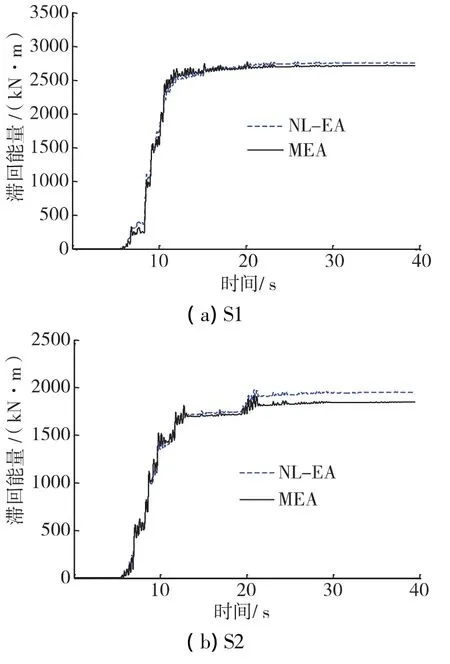
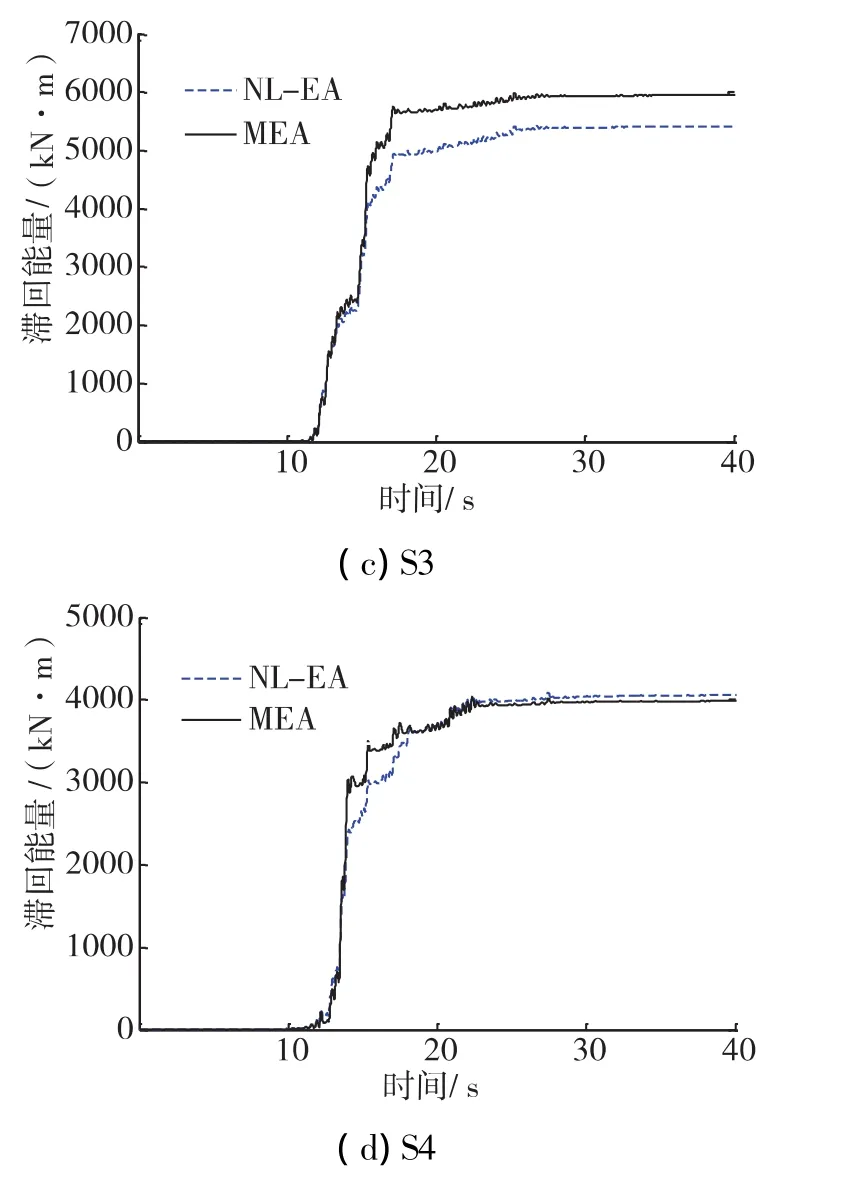
圖3 軟土場地下通過MEA法和NL-EA法計算得到的滯回能量時程比較
3 結論
借鑒模態Pushover分析理論的思路,假設結構的彈塑性能量反應近似等于結構模態分解后各階模態能量反應的疊加,用“等效振型”替代彈性振型,通過推導得到結構模態等效SDOF體系能量值與結構模態反應能量值的關系,進而建立通過模態能量分析估算結構滯回能量的方法。按硬、中、軟土三類場地設計3座6層建筑,采用三類場地選取的12條地震動作為激勵進行能量分析,結果表明:
(1)通過MEA方法得到的結構整體滯回能量時程在趨勢上與精確解符合較好;
(2)對于高振幅持時較短或出現少數明顯峰值加速度的地震動,MEA方法的能量估算偏差較小;而對于高振幅持時較長的地震動,MEA方法的能量估算偏差較大。
[1]HABIBI A,CHAN R W K,ALBERMANI F.Energybased design method for seismic retrofitting with passive energy dissipation systems[J].Engineering Structures,2013,46:77-86.
[2]BENAVENT C A.A energy-based method of seismic retrofit of existing frames using hysteretic dampers[J].Soil Dynamics and Earthquake Engineering,2011,31:1385-1396.
[3]LEELATAVIWAT S,GOEL S C.Energy-based seismic design of structures using yield mechanism and target drift[J].Journal of Structural Engineering,ASCE,2002,128(8):1046-1054.
[4]AMIRI G G,DARZI G A,AMIRI J V.Design elastic input energy spectra based on Iranian earthquakes[J].Canadian Journal of Civil Engineering,2008,35:635–646.
[5]BENAVENT C A,LOPEZ A F,BRAVO G D A.Design energy input spectra for moderate-to-high seismicity regions based on Colombian earthquakes[J].Soil Dynamics and Earthquake Engineering,2010,30:1129-1148.
[6]DANNY A,MARIO O.On the estimation of hysteretic energy demands for SDOF systems[J].Earthquake Engineering and Structural Dynamics,2007,36:2365-2382.
[7]公茂盛,謝禮立.地震動滯回能量譜衰減規律研究[J].地震工程與工程振動,2004,24(2):8-14.
[8]CHOU C C,UANG C M.Establishing absorbed energy spectra an attenuation approach[J].Earthquake Engineering and Structure Dynamics,2000,29:1441-1455.
[9]陳逵,劉哲鋒.結構瞬時輸入能量反應持時譜的研究[J].工程力學,2011,28(1):19-25.
[10]劉哲鋒,沈蒲生.鋼框架-鋼筋混凝土剪力墻結構的地震能量反應分析[J].地震工程與工程振動,2007,27(2):69-73.
[11]WONG K K F,LIU R.Evaluation of Seismic Energy in Structures with Rigid-end Offsets[C].The 18th Analysis and Computation Specialty Conference,ASCE,2008.
[12]陸鐵堅,秦素娟.高層鋼-混凝土混合結構地震作用下的能量反應分析[J].計算力學學報,2010,27(3):490-495.
[13]經杰,葉列平,錢稼茹.不均勻剪切型層模型結構基于能量概念的彈塑性地震位移反應分析[J].土木工程學報,2003,36(12):14-19.
[14]胡冗冗,王亞勇.剪切型多自由度體系瞬時輸入能量的分布[J].世界地震工程,2006,22(4):140-144.
[15]常磊,葉獻國.結構能量反應的振型分解法研究[J].合肥工業大學學報,2010,33(7):1035-1038.

