鍋爐汽包瞬態溫度場在線監測

李 斌， 陳 豐， 史良宵

（華北電力大學 能源動力與機械工程學院，河北保定071003）

溫度場計算是汽包應力計算和疲勞壽命分析的基礎，根據瞬態溫度場，可實時監測汽包疲勞壽命損耗，保證機組安全經濟運行［1－5］.

傳統的汽包溫度場計算通常采用直接解法［6］，即在一定的初始條件和邊界條件下求解導熱微分方程，它需要已知求解區域的所有邊界條件.由于汽包內有各種復雜的流動和換熱過程，因而采用該方法時需要進行很多假設，從而帶來較大的計算誤差.另外，直接解法最致命的缺陷是需要知道汽包內壁與水和水蒸氣的對流傳熱系數，而汽包內復雜的工況使得很難得到確切的傳熱系數，通常采用經驗數據，但會導致誤差［7－10］.此外還要已知熱流密度和流體溫度，盡管熱流密度和流體溫度都可以通過熱流密度計和熱電偶測得，然而該數據只適用于低壓情況下，不適用于工程實際高溫高壓或者不便布置傳感器等情況下瞬態傳熱的計算.

反演解法（Inverse Method）［11－12］采用控制容積法，在控制體上選擇一些離散的測點，采用熱電偶測溫，通過測得的溫度值實現整個溫度場的求解，即導熱反問題（Inverse Problem of Heat Conduction）求解［13－14］.采用反演解法求解大型高溫高壓設備溫度場不需要進行直接解法中的假設，僅需要知道高溫高壓設備外壁的溫度，即可快捷準確地計算出該設備的溫度場.計算汽包的溫度場時，汽包外壁的溫度可以通過在汽包外壁布置熱電偶進行測量，比較準確和方便.該方法克服了直接解法中的缺陷，不需要知道汽包內壁的傳熱系數便可求解汽包溫度場.

1 反演解法

應用反演解法實現汽包瞬態溫度場的在線監測，首先在汽包的外壁布置測點，安裝熱電偶測取外壁溫度，然后根據測點對汽包橫截面進行網格劃分，最后利用控制容積法對導熱微分方程進行離散，將局部熱傳導方程轉化為常微分方程，由外向內逐次內推，求解得到汽包橫截面的溫度場.

汽包橫截面示意圖見圖1，圖中kw、ks分別表示汽包內飽和水.飽和水蒸氣與汽包內壁的對流傳熱系數，W／（m2·K）.

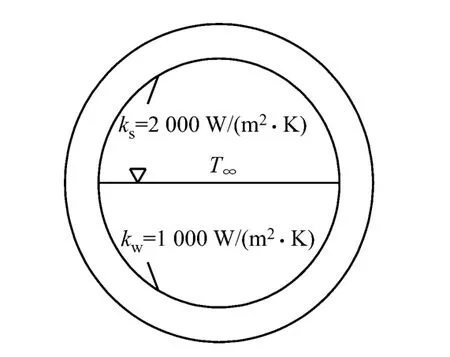
圖1 汽包橫截面示意圖Fig.1 Sectional view of the boiler drum

汽包模型相關參數如下：內徑r1為0.400m，外徑r5為0.426m；汽包材料的物性參數：導熱系數λ為36.0W／（m·K），密度ρ為7 850kg／m3，比熱容c為468J／（kg·K）.

1.1 網格劃分

根據汽包橫截面外壁熱電偶的布置情況，結合反演解法的思想對其進行網格劃分，見圖2.圖中，r1和r5分別為內徑和外徑，m；r2、r3和r4分別表示中間各層半徑，m.由于汽包橫截面的對稱性，只繪制右半部分.沿著半徑方向由內向外劃分為三層，分別為內層、中間層和外層，沿圓周方向劃分為13個節點.

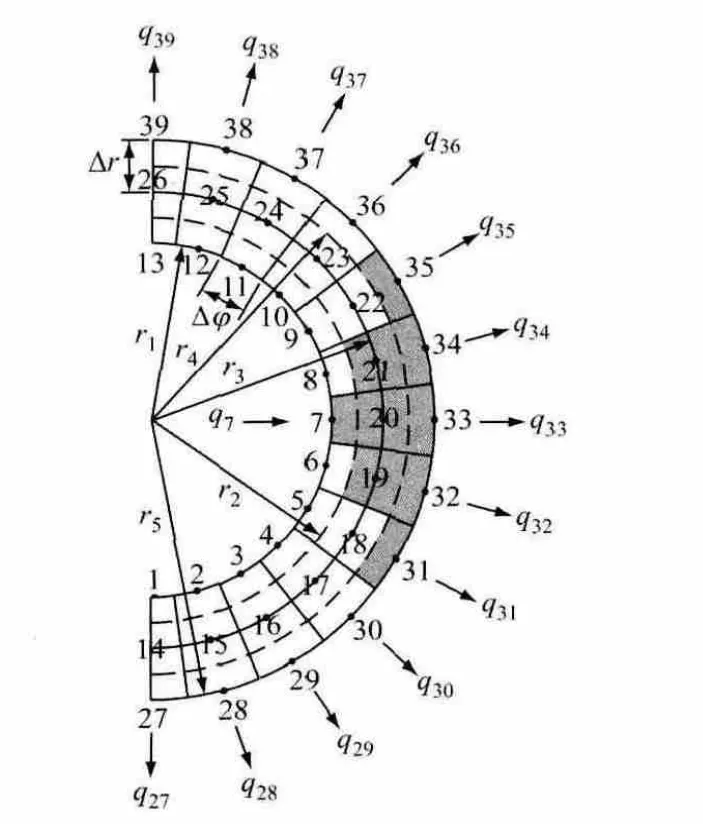
圖2 反演解法網格劃分示意圖Fig.2 Grid division of inverse method

1.2 反演解法

根據已知的外壁溫度和熱流密度，按照導熱問題數值解法的思想，采用熱平衡法，對汽包外壁每個節點所代表的控制容積用傅里葉定律列出能量守恒表達式.外層節點32、節點33和節點34的能量守恒表達式如下：

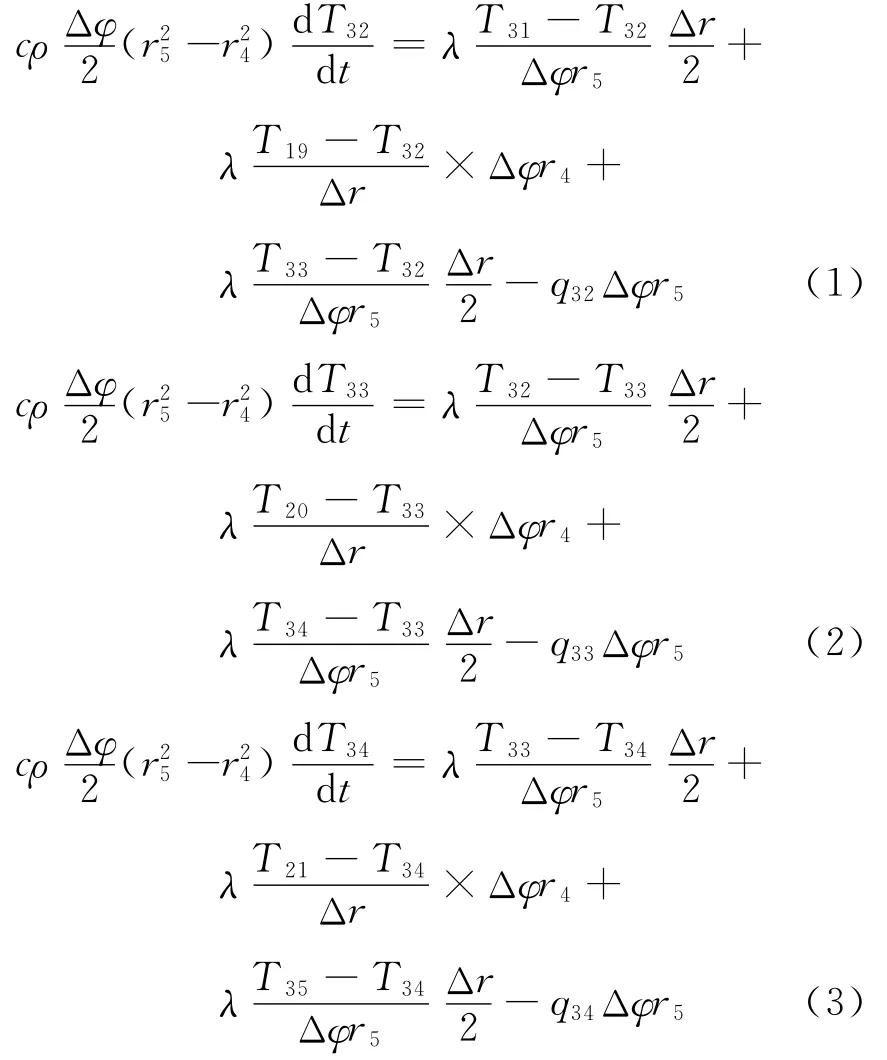
式中：Δφ為容積角度變化量，rad；Δr為容積徑向變化量，m；Ti為節點i的溫度，℃；qi為節點i處的熱流密度，W／m2.

根據式（1）、式（2）和式（3）可以得出中間層節點19、節點20和節點21的溫度表達式：

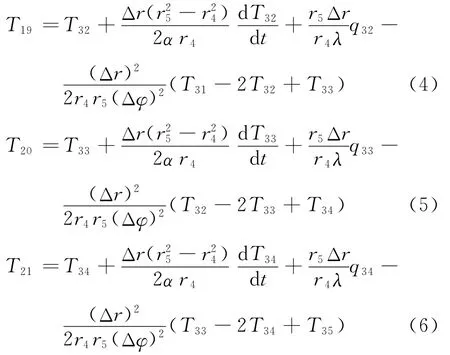
同理，根據圖2，對中間層節點20列出能量守恒表達式，得到內層節點7的溫度表達式：

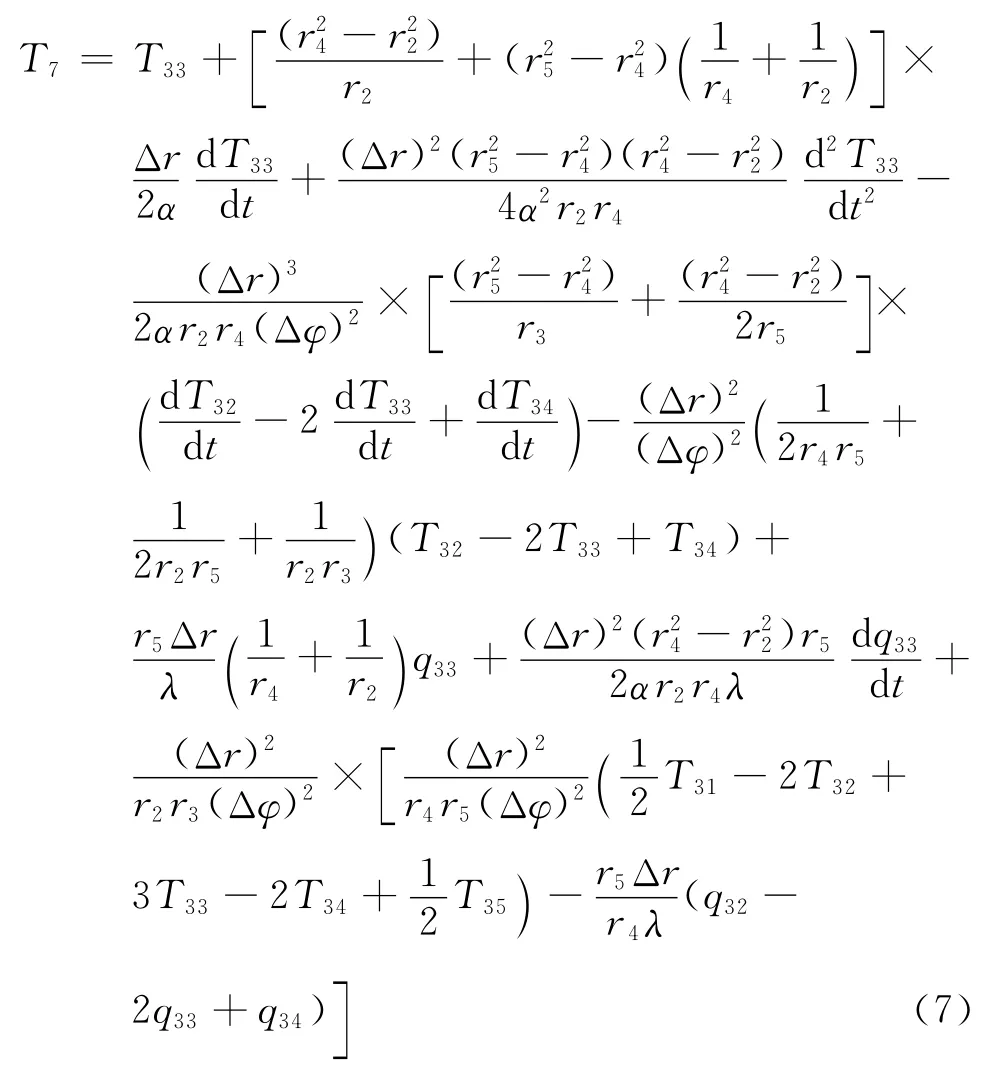
將外層節點的溫度逐次反演求解得到內層節點的溫度，改變外層節點位置可求解得到整個內層節點的溫度，從而得到整個汽包橫截面的瞬態溫度場.

2 Ansys分析驗證

由于采用反演解法求解溫度場需要知道求解區域外邊界的溫度及其邊界換熱條件，因此采用Ansys數值模擬計算結果進行相關驗證.

根據導熱微分方程、求解區域的邊界條件以及初始條件，采用Ansys進行數值求解，將求解得到的外邊界的溫度作為反演解法的已知條件，通過反演解法求解得到內層節點溫度，再與Ansys數值模擬得到的內層節點溫度進行比較.

2.1 Ansys數值模擬數學模型的建立

導熱微分方程：

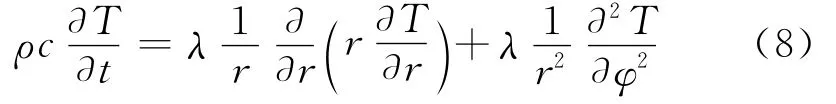
邊界條件：

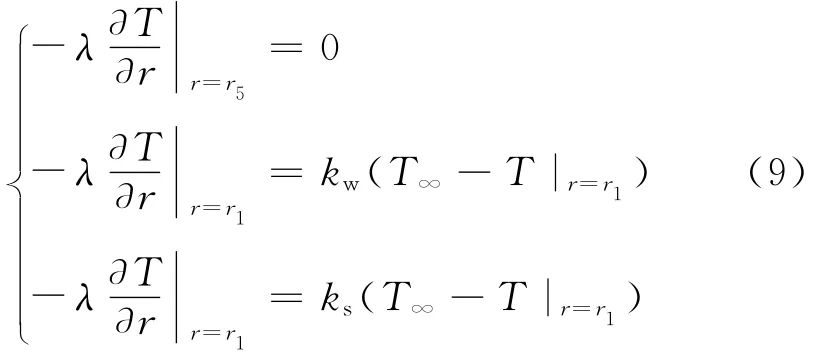
初始溫度：

汽包內飽和水（或飽和水蒸氣）的溫度隨時間的變化關系如下：

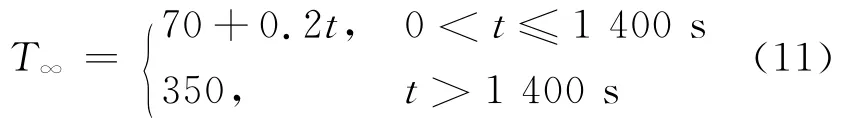
式中：t為時間，s；T∞為流體溫度，℃.

Ansys數值模擬的網格劃分如圖3所示.由于對象具有對稱性，故取其右半部分進行分析.沿徑向劃分為5個節點，周向25個節點，共計96個單元，125個節點.

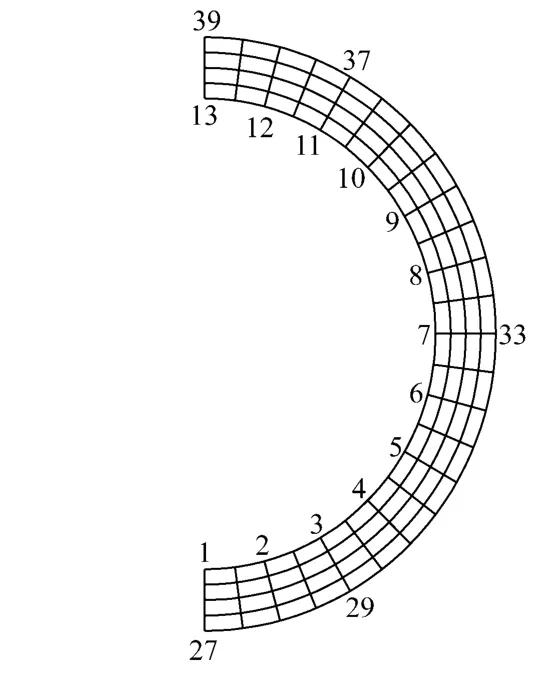
圖3 Ansys數值模擬網格劃分Fig.3 Grid division of Ansys numerical simulation

2.2 數值模擬

按照上述模型對汽包橫截面瞬態溫度場進行數值模擬，截面的初始溫度為70℃，模擬的時間步長為10s，終止時刻為3 000s，得到汽包橫截面的節點溫度隨時間的變化曲線如圖4所示.圖中節點29、節點33和節點37為外層節點，節點3和節點11為內層節點.

2.3 結果驗證

將上述Ansys數值模擬得到的外層節點溫度作為反演解法的已知條件（即測量外壁溫度），時間步長同樣取10s，逐漸內推得到相應的內層節點溫度，并與Ansys模擬所得的內層節點溫度進行比較驗證.

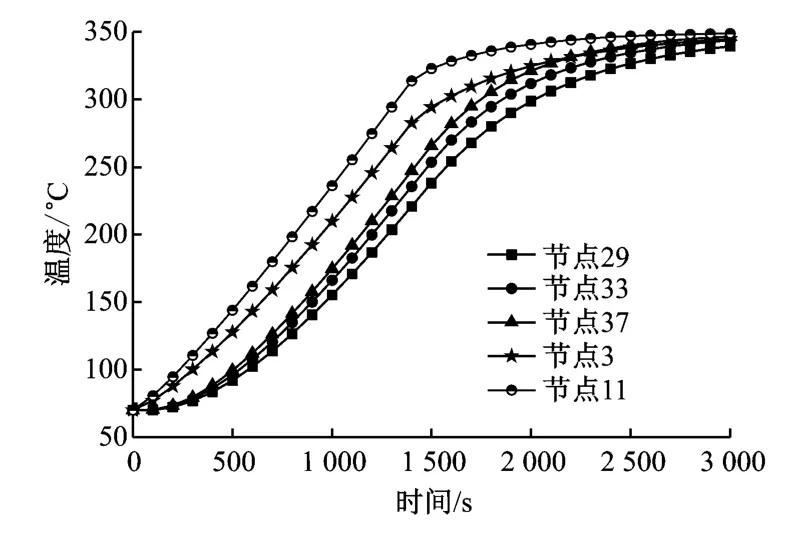
圖4 Ansys數值模擬所得汽包橫截面的節點溫度隨時間的變化Fig.4 Variation of node temperature with time obtained by Ansys numerical simulation

由于采用反演解法求解溫度值時需用到溫度對時間的高階導數，且測量的外邊界的溫度對時間的變化非常敏感，在逐層推進的過程中，溫度值隨時間的變化產生的誤差被逐層放大，因此，為減小誤差，在計算前對外壁絕熱層的溫度測量值及外壁溫度對時間的導數進行修正，采用局部多項式方法對外層溫度值進行空間和時間的平滑后再進行計算［8］.

Ansys模擬所得外層節點溫度經過相應的平滑后，得到的外層節點溫度隨時間的變化曲線如圖5所示.

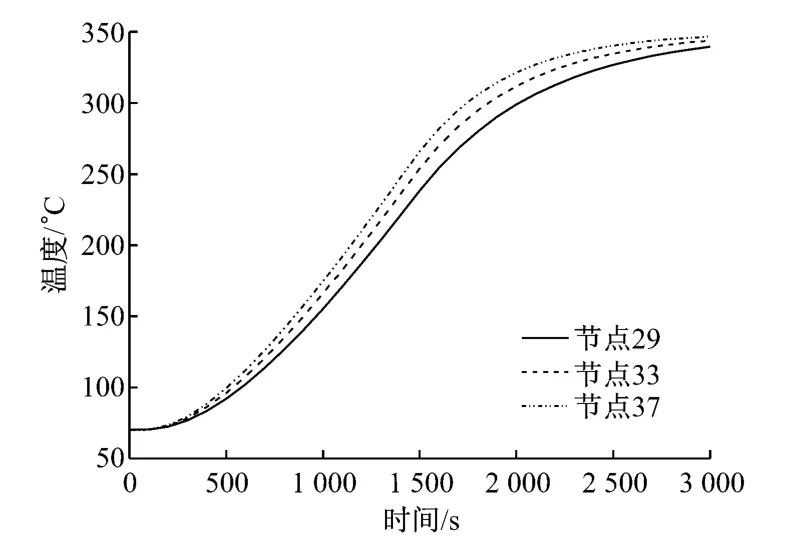
圖5 經空間、時間平滑后的外層節點29、節點33和節點37的溫度Fig.5 Space－time averaged value of temperature at outer nodes 29，33and 37

根據圖1，以汽包橫截面幾何中心線作為汽水分界面，下部飽和水（上部飽和水蒸氣）與內壁發生對流傳熱，各點處溫差相對比較小，因此在進行反演解法驗證時，中心線以下、中心線處以及中心線以上三部分分別采用節點29、節點33和節點37的溫度作為相應的外層溫度.

反演解法的計算結果與Ansys數值模擬結果的對比如圖6所示，2種算法計算所得的t＝1 000s和t＝2 000s時部分節點的溫度值如表1和表2所示.由圖6、表1和表2可以看出，反演解法的計算結果與Ansys數值模擬結果具有較高的吻合度，說明反演解法具有較高的精確度.

圖6 反演解法和Ansys模擬所得內層節點3和節點11溫度值的對比Fig.6 Comparison of temperature changes at internal nodes 3and 11by inverse method and Ansys numerical simulation

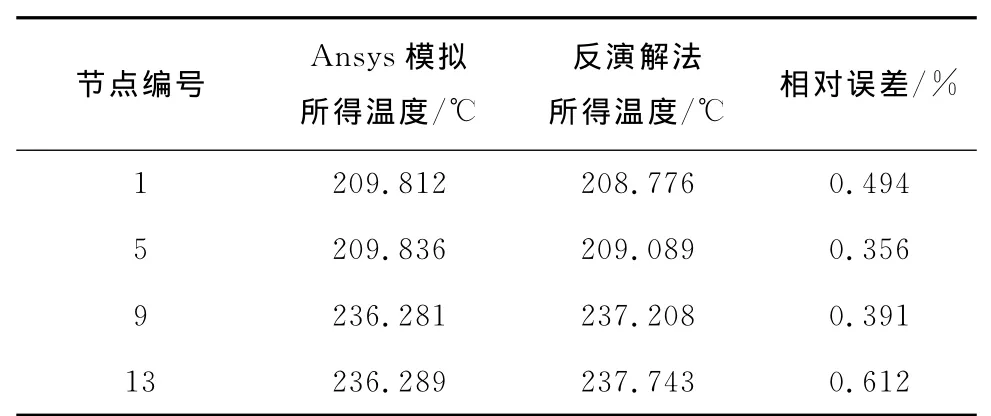
表1 t＝1 000s時2種算法計算所得部分節點的溫度值Tab.1 Comparison of temperature changes at partial nodes obtained by two methods at t＝1 000s

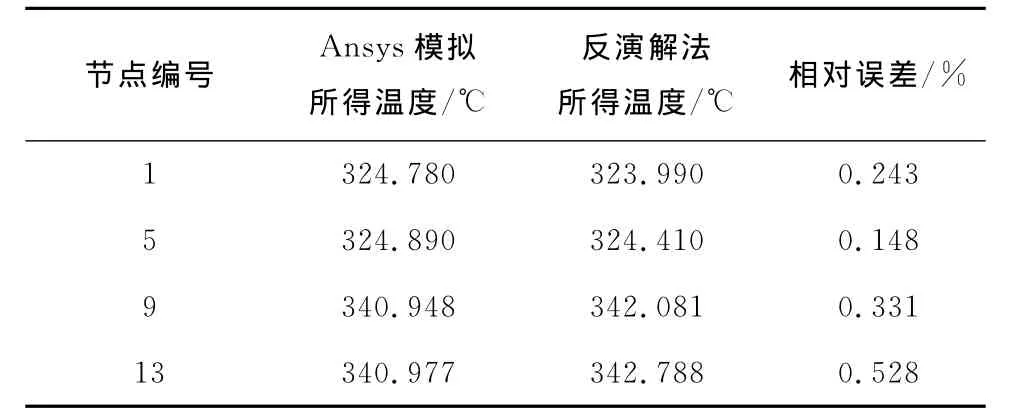
表2 t＝2 000s時2種算法計算所得部分節點的溫度值Tab.2 Comparison of temperature changes at partial nodes obtained by two methods at t＝2 000s

3 無限長圓柱理論解驗證

3.1 模型的建立

半徑為R的實心圓柱，其材料的導熱系數為λ，熱擴散率α為常數，初始溫度為T0，將其放在溫度為Tf并保持不變的流體中發生對流傳熱，流體與圓柱表面間的表面傳熱系數k為常數.其模型簡化示意圖如圖7所示.

3.2 理論解析解

圓柱的無量綱過余溫度解析解為

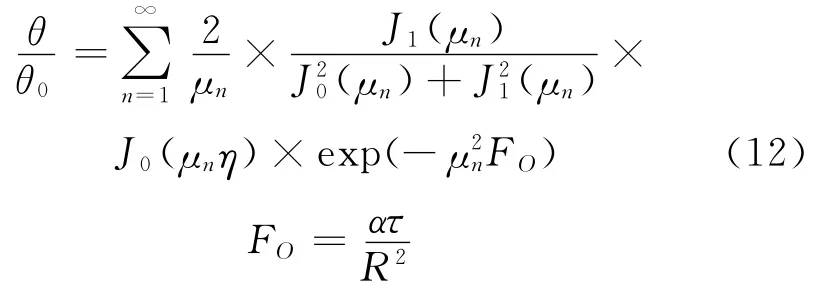
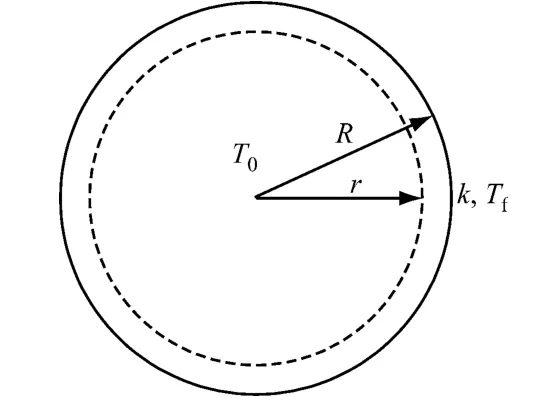
圖7 理論解模型示意圖Fig.7 Model for analytical solution

式中：FO為傅里葉數；η為半徑比；τ為時間，s；r為計算半徑，m；θ為過余溫度，K；θ0為初始時刻過余溫度，K；J0、J1分別為零階和一階的第一類貝塞爾（Bessel）函數；μn為超越方程的特征值；k為對流傳熱系數，W／（m2·K）；λ為材料導熱系數，W／（m·K）；

選取初始溫度為500℃，流體溫度為20℃，計算時間步長為1s，對流傳熱系數為845W／（m2·K），根據理論解析解得到r＝r1和r＝r5處的溫度值，如圖8所示.

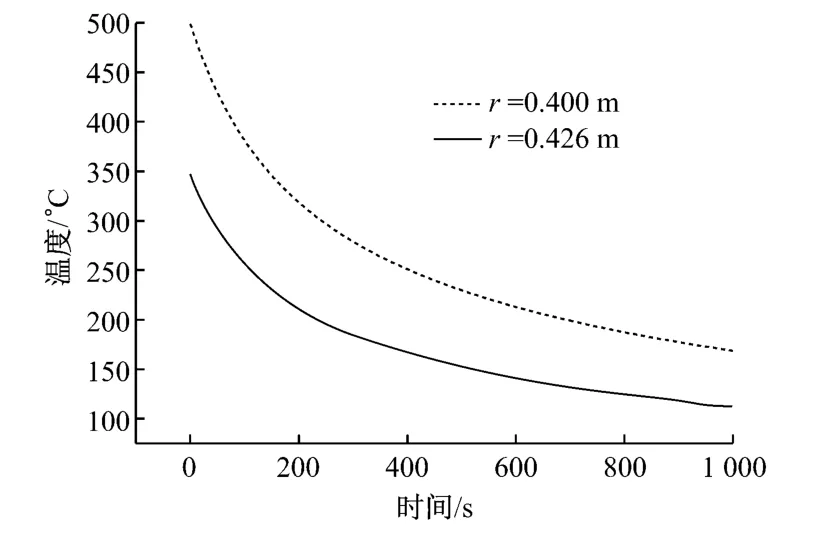
圖8 無限長圓柱r＝r1和r＝r5處的理論解析解Fig.8 Analytical solution for infinitely long cylinder in the case of r＝r1and r＝r5

3.3 結果驗證

將無限長圓柱r＝r5（即外層）處的理論解析解作為“測量外層溫度”，用作反演解法的已知條件進行反演計算.將求解得到的結果與無限長圓柱r＝r1（即內層）處的理論解析解進行對比分析驗證，如圖9所示.

相對于實際熱電偶測量的外層數據而言，理論解析解波動或者誤差更小，因此為了驗證應用測量數據進行反演解法計算的正確性，在外層理論解析解的基礎上增加一個隨機誤差－0.5～0.5K，再作為“測量外層溫度”進行反演解法計算.帶擾動情況下內層理論解析解與反演解法結果的對比見圖10.

由圖9和圖10可知，反演解法結果與理論解析解很接近，吻合度高，同時外加擾動情況下結果也比較接近，可以驗證反演解法具有較高的精確度.

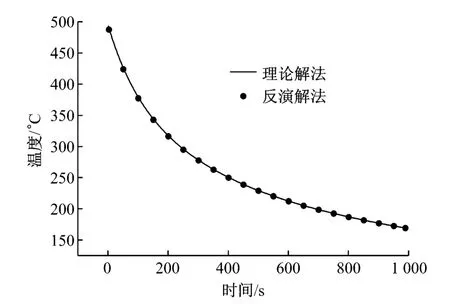
圖9 內層反演解法結果與理論解析解的對比Fig.9 Comparison of temperature changes respectively obtained by inverse method and analytical solution

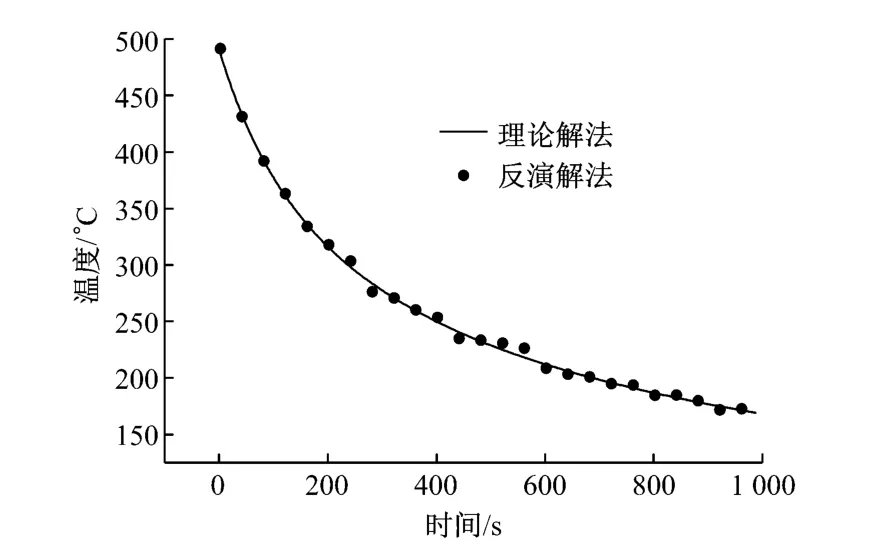
圖10 帶擾動情況下內層理論解析解與反演解法結果的對比Fig.1 0 Comparison of temperature changes respectively obtained by inverse method and analytical solution with disturbances

4 試驗驗證

為了驗證反演解法的計算精度，在某小型鍋爐外壁安裝熱電偶進行實際數據測量，將計算結果與測得的試驗數據進行比較，對該方法進行驗證.

選擇鍋爐的某一段工況，在鍋爐外壁選擇適當的位置布置相應的熱電偶，布置的外壁測點編號為35～39，內壁測點編號為11，如圖2所示.

由于實際現場測量數據存在較大的波動，首先將鍋爐外壁的測量數據按照反演解法的步驟進行時間和空間的平滑處理，然后進行計算，即可求解得到內壁測點11的溫度隨時間的變化.再將計算結果與實際熱電偶測量結果進行對比分析，如圖11所示.

由于實際運行工況的復雜性，實際測量結果存在一定的波動，另外熱電偶測量數據本身存在一定的誤差，但是由圖11可知，反演解法的計算結果與熱電偶的實際測量結果吻合度較高.

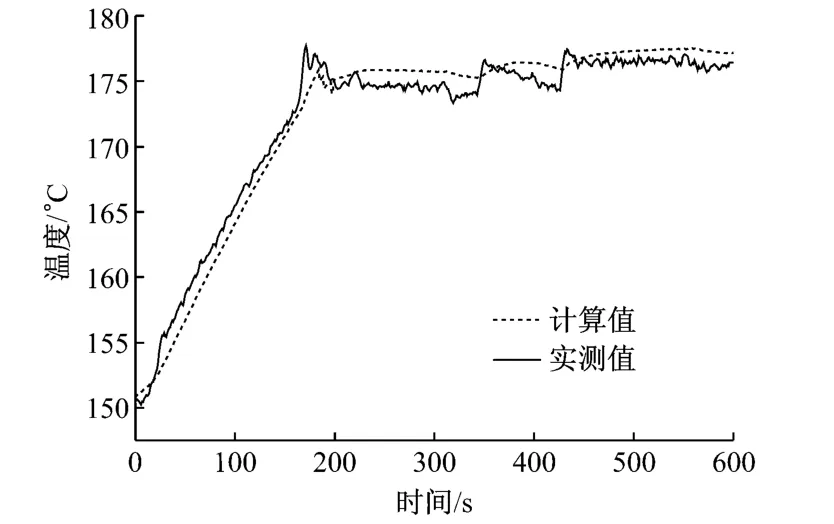
圖11 內壁測點11溫度的計算結果與實測結果的對比分析Fig.1 1 Comparison of temperature changes at node 11obtained by inverse method and experimental test

5 結 論

（1）反演解法思路簡單明了，求解過程不需要迭代，計算精度高，相對于直接解法而言，求解網格相對較少，但是精度卻一致.另外計算不需要已知內壁換熱條件，只需知道外層節點的溫度即可反演得到內層節點溫度，從而得到整個汽包的瞬態溫度場分布.同時也避免了打孔對壓力容器造成的設備壽命損耗，提高了設備的使用壽命.

（2）通過Ansys數值模擬，取汽包外壁邊界換熱條件為絕熱，從二維瞬態的角度來驗證反演解法的計算結果，證明該方法計算精度高，二者具有很好的吻合度.

（3）采用無限長圓柱理論解析解，圓柱體外壁邊界與流體對流傳熱，從一維瞬態的角度驗證反演解法的適用范圍，同時驗證了其計算的準確性；另外在附加擾動的情況下同樣得到很好的吻合度.

（4）通過與實際試驗數據的對比分析，驗證了反演解法具有較高的計算精度，與實際試驗數據具有很好的吻合度，滿足工程應用的要求.

［1］管德清，莫江春，張學綸，等.電站鍋爐汽包壽命在線監測系統［J］.動力工程，2002，22（6）：2044－2047.GUAN Deqing，MO Jiangchun，ZHANG Xuelun，et al.Life on－line monitoring system for boiler drum of power station［J］.Power Engineering，2002，22（6）：2044－2047.

［2］劉彤，徐鋼，龐力平，等.鍋爐爐內承壓部件的蠕變分析及壽命計算［J］.動力工程，2004，24（5）：631－635.LIU Tong，XU Gang，PANG Liping，et al.Creep analysis and life calculation of the pressure components inside boiler［J］.Power Engineering，2004，24（5）：631－635.

［3］李立人，陳瑋，盛建國，等.鍋爐受壓元件的高溫蠕變－疲勞壽命設計計算方法［J］.動力工程，2009，29（5）：409－416.LI Liren，CHEN Wei，SHENG Jianguo，et al.Creepfatigue life design and calculation method for boiler pressure elements under elevated temperature［J］.Journal of Power Engineering，2009，29（5）：409－416.

［4］鄭心偉，孫瑜，王曉軍.增壓鍋爐汽包低周疲勞壽命計算方法研究［J］.熱能動力工程，2010，25（2）：184－189.ZHENG Xinwei，SUN Yu，WANG Xiaojun.Study of the methods for calculating the low－cycle fatigue life of a supercharged boiler drum ［J］.Journal of Engineering for Thermal Energy and Power，2010，25（2）：184－189.

［5］張健.超臨界鍋爐爐外承壓部件的壽命分析及在線檢測［D］.北京：華北電力大學，2008.

［6］趙鐵成，沈月芬，朱國楨，等.電站鍋爐鍋筒溫度場計算——三維非穩態變物性材料不均勻導熱問題有限元分析［J］.中國電機工程學報，1997，17（4）：217－220.ZHAO Tiecheng，SHEN Yuefen，ZHU Guozhen，et al.Temperature field calculation of boiler drum—finite element analysis of 3－D unsteady variable character uneven material heat conduction problem［J］.Proceedings of the CSEE，1997，17（4）：217－220.

［7］HàO D N，THANH P X，LESNIC D.Determination of the heat transfer coefficients in transient heat conduction［J］.Inverse Problems，2013，29（9）：095020.

［8］TALER J.Determination of local heat transfer coefficient from the solution of the inverse heat conduction problem ［J］.Forschung im Ingenieurwesen，2007，71（2）：69－78.

［9］CEBULA A，TALER J.Determination of transient temperature and heat flux on the surface of a reactor control rod based on temperature measurements at the interior points ［J］.Applied Thermal Engineering，2014，63（1）：158－169.

［10］HU Wensen，LI Bin，CAO Zidong，et al.An inverse method for online stress monitoring and fatigue life analysis of boiler drums［J］.Journal of Chongqing University：English Edition，2009，8（2）：89－96.

［11］JAREMKIEWICZ M，TALER D，SOBOTA T.Measuring transient temperature of the medium in power engineering machines and installations［J］.Applied Thermal Engineering，2009，29（16）：3374－3379.

［12］TALER J.A new space marching method for solving inverse heat conditions problems ［J］.Forschung im Ingenieurwesen，1999，64（11）：296－306.

［13］TALER J，ZIMA W.Solution of inverse heat conduction problems using control volume approach［J］.International Journal of Heat and Mass Transfer，1999，42（6）：1123－1140.

［14］WANG Peng，LI Bin，WANG Songling.An On－line fatigue life monitoring system for boiler drums based on the inverse problem of heat conduction method［J］.Advanced Materials Research，2012，413：361－366.