基于NSS模型的利率期限結構影響因子的時間序列分析

張啟坤

（安徽財經大學 金融學院，安徽 蚌埠 233030）

1 引言

利率期限結構是指同等風險水平、不同期限下的債券即期利率與剩余期限的關系，又被稱為收益率曲線.研究利率期限結構首先要解決的問題是估計不同期限的即期利率，國內外學者提出了很多估計方法.不少實證分析表明，NS模型及其擴展模型擬合效果穩健，預測能力較強.國際清算銀行（BIS）2005年的資料顯示，世界主要發達國家的中央銀行也多用NS模型或NSS模型估算利率期限結構.NS模型類似于描述利率動態變化的微分方程解的形式，NSS模型是在NS模型基礎上增加了一個擴展項，允許收益率曲線有兩個極值點，解決了NS模型不能反映收益率曲線復雜形狀的問題.NSS模型中即期利率函數為：

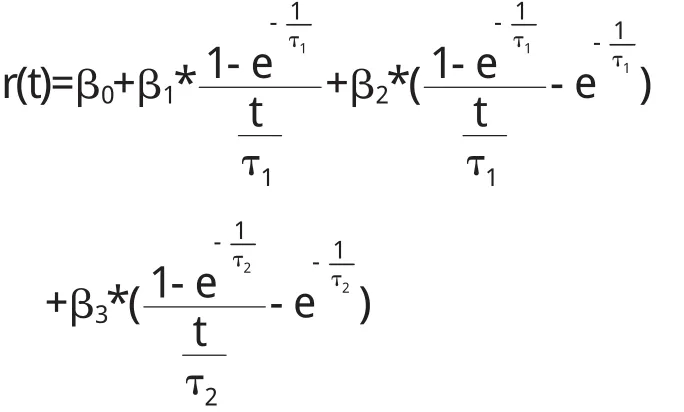
其中 t是剩余期限，β0、β1、β2、β3、τ1、τ2是待估參數，τ1、τ2需要事先設定初始值.NSS模型具有很強的經濟含義：β0反映了收益率曲線的長期水平，被稱為水平因子；β1反映了收益率曲線的傾斜程度，被稱為斜度因子；β2反映了收益率曲線的彎曲程度，被稱為曲度因子；β3對彎曲程度起著微調作用，被稱為曲度調整因子；τ1、τ2控制收益率曲線極值點出現的位置.很多主成分分析的實證研究也證實了四個因子足夠解釋國債收益率變動.利率期限結構的研究不能只是關注模型的構造，還應該討論相關的時間序列分析，本文作者認為由于NSS模型的四個參數 β0、β1、β2、β3從不同方面描述了收益率曲線的特征，故它們包含的經濟信息具有很強的時間序列相關性，分析這四個參數對認識和應用利率期限結構有著重要的研究意義.目前一些文獻用時間序列模型分析利率期限結構的影響因子與宏觀經濟變量、貨幣政策變量之間的關系，還有一些文獻用利率期限結構影響因子的時間序列模型擬合樣本外的收益率曲線，本文的研究過程基本參照后者的思路：建立NSS模型中利率期限結構影響因子的VAR模型，分析各影響因子的動態特征，并嘗試對樣本外各影響因子進行預測.

2 數據說明與模型的建立

由于歷史的原因，我國的國債市場分離為銀行間國債市場和交易所國債市場.銀行間國債市場交易量大，而交易所國債市場流通性強，兩個市場都有學者研究.通過前期的數據分析，本文作者發現用交易所國債市場的樣本得出的β序列有的平穩，有的二階差分仍不平穩，無法進行Johansen協整和向量自回歸，調整樣本區間仍然不能解決問題.為了研究的方便，本文選取2004年11月至2012年10月每月最后一個交易日的銀行間國債數據作為研究對象.由于我國處于利率市場化改革時期，過早的數據可能不適宜做擬合，故時間跨度沒有選擇更長.以上數據分為兩部分，2004年11月至2011年10月的數據用作樣本內擬合，2011年11月至2012年10月的數據用作樣本外預測.從銳思數據庫可以查到NSS模型每一天的參數值，以下將使用Eviews軟件對2004年11月至2011年10月的數據進行VAR模型的擬合.

2.1 相關性檢驗

相關性矩陣如下所示：

相關性矩陣顯示 β0、β1、β2、β3之間具有高度的相關性，尤其是β0與β1、β2與β3之間相關性超過90%.

2.2 單位根檢驗

由于是月度數據，滯后期可以選擇12，使用的信息準則為AIC準則.

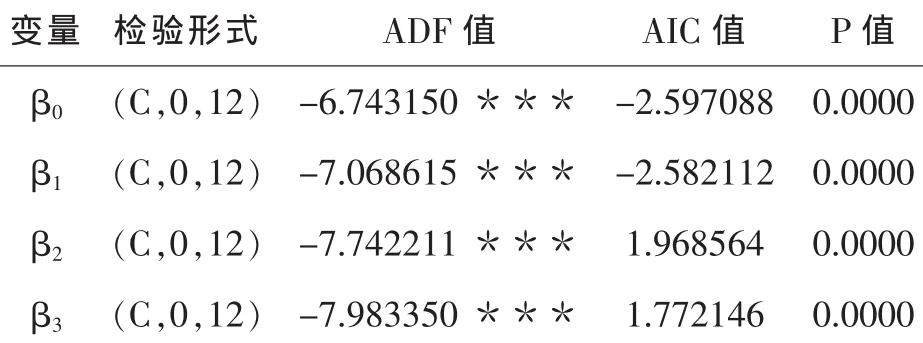
表1 變量ADF檢驗結果

從表 1可以看出變量 β0、β1、β2、β3都是平穩序列，不需要進行協整以及誤差修正.

2.3 建立VAR模型

由表2可以看出幾乎各準則都取滯后階數為1，故VAR模型滯后階數可以定為1.由此得到的VAR模型為：

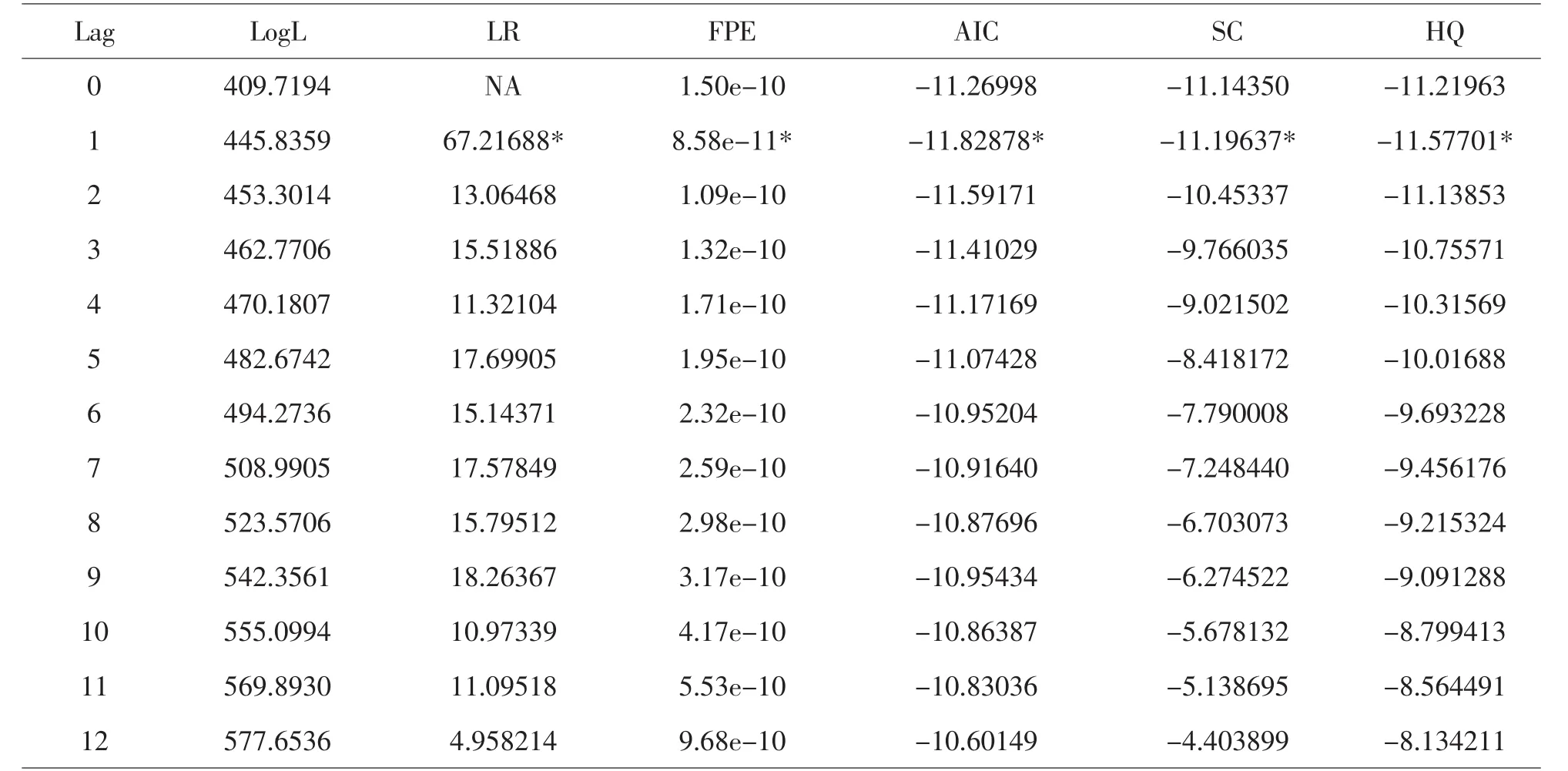
表2 不同滯后階數的信息準則

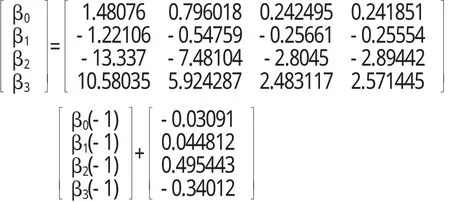
但是四個方程的擬合優度都不超過12%，模型擬合效果很差.

2.4 VAR模型穩定性檢驗

由圖1可以看出：所有根模的倒數都落在單位圓內，說明所建立的VAR模型是穩定的.

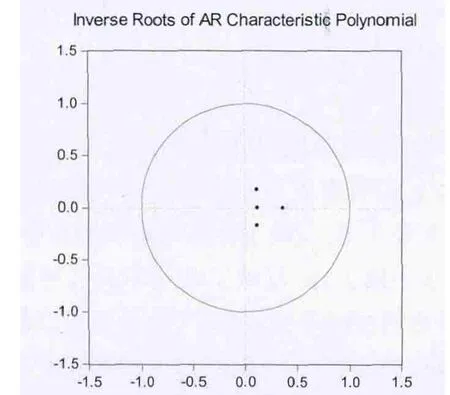
圖1 VAR模型穩定性檢驗

3 模型的檢驗

3.1 脈沖響應

從圖2可以看出：對于β0的一個Cholesky標準差新息的沖擊，β1、β2、β3都沒有立即反應，之后β1、β2、β3都有正向反應.β1、β2微弱上升，β3在開始2個月小幅上升，3個月之后 β1、β2、β3均下降.對于β1的一個Cholesky標準差新息的沖擊，β0立即有非常顯著的逆向反應，之后不斷減弱.β2、β3逆向反應，β2反應微弱.對于β2的一個Cholesky標準差新息的沖擊，β0、β1立即有逆向反應，β0的逆向反應非常顯著，之后不斷減弱.β3逆向反應持續增強至2個月，之后不斷減弱.對于β3的一個Cholesky標準差新息的沖擊，β0立即有正向反應，β1、β2立即有逆向反應，β2反應非常顯著，之后不斷減弱.β3在開始2個月上升，之后不斷減弱.

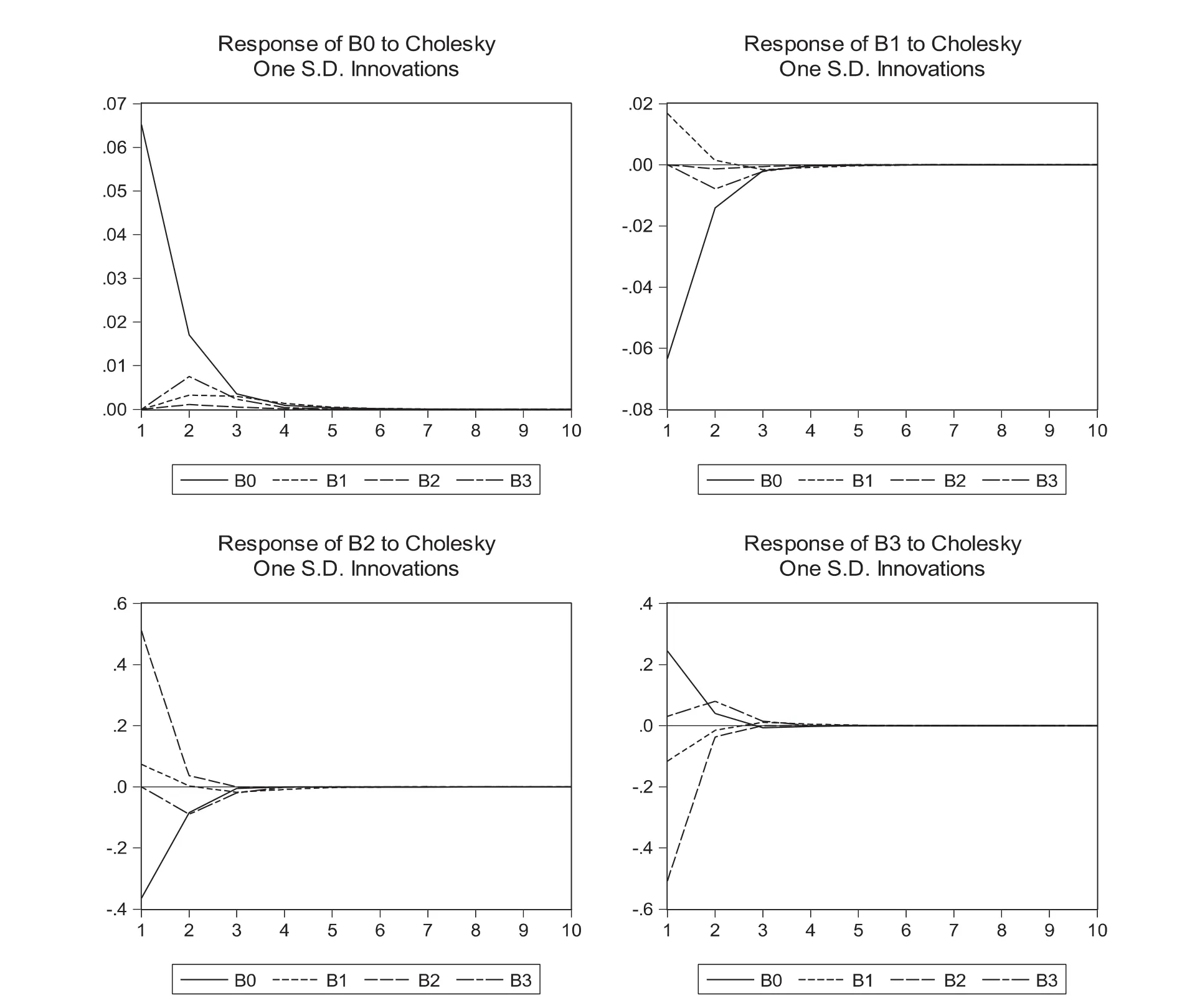
圖2 脈沖響應結果

3.2 方差分解

從圖 3可以看出：總體上 β0、β1、β2、β3變動的影響隨步長的增加處于基本穩定的狀態.β0的變動主要受自身沖擊的影響.β1的變動受β0的影響很大，比重占92%以上，受自身影響的比重僅僅占6%.β2的變動受自身影響的比重占63%以上，受β0的影響占 33%.β3的變動主要受 β2、β0的影響，比重分別占75%和18%以上.

4 模型的預測

根據胡志強、王婷①對NS模型三個因子的研究，β0、β2未來30天及60天的預測值與估計值相差僅為幾個百分比，說明預測較為準確；β1則產生比較明顯的偏差，三期以后的偏差都比較大，已經不具有參考價值.本文利用建立的VAR方程對2011年11月至2012年10月的參數值進行預測，結果顯示：第一期預測除β2擬合值接近NSS模型的 β2估計值外，β0、β1、β3預測偏差過大，β3的符號甚至預測相反，以后各期更無參考價值，故本文通過建立VAR模型來預測未來利率期限結構是不可行的.原因可能是NS模型更簡潔，參數含義更明確，而NSS模型中β2、β3均是中期利率的影響因素，而VAR模型同等地對待β2、β3與經濟含義相對獨立的β0、β1.相關性矩陣表明β0與β1相關性很強，β2與 β3相關性很強，本文嘗試將 β0、β1和 β2、β3分開進行向量自回歸.對β0、β1進行向量自回歸，根據信息準則判斷滯后階數為1，由此得到的VAR方程為：

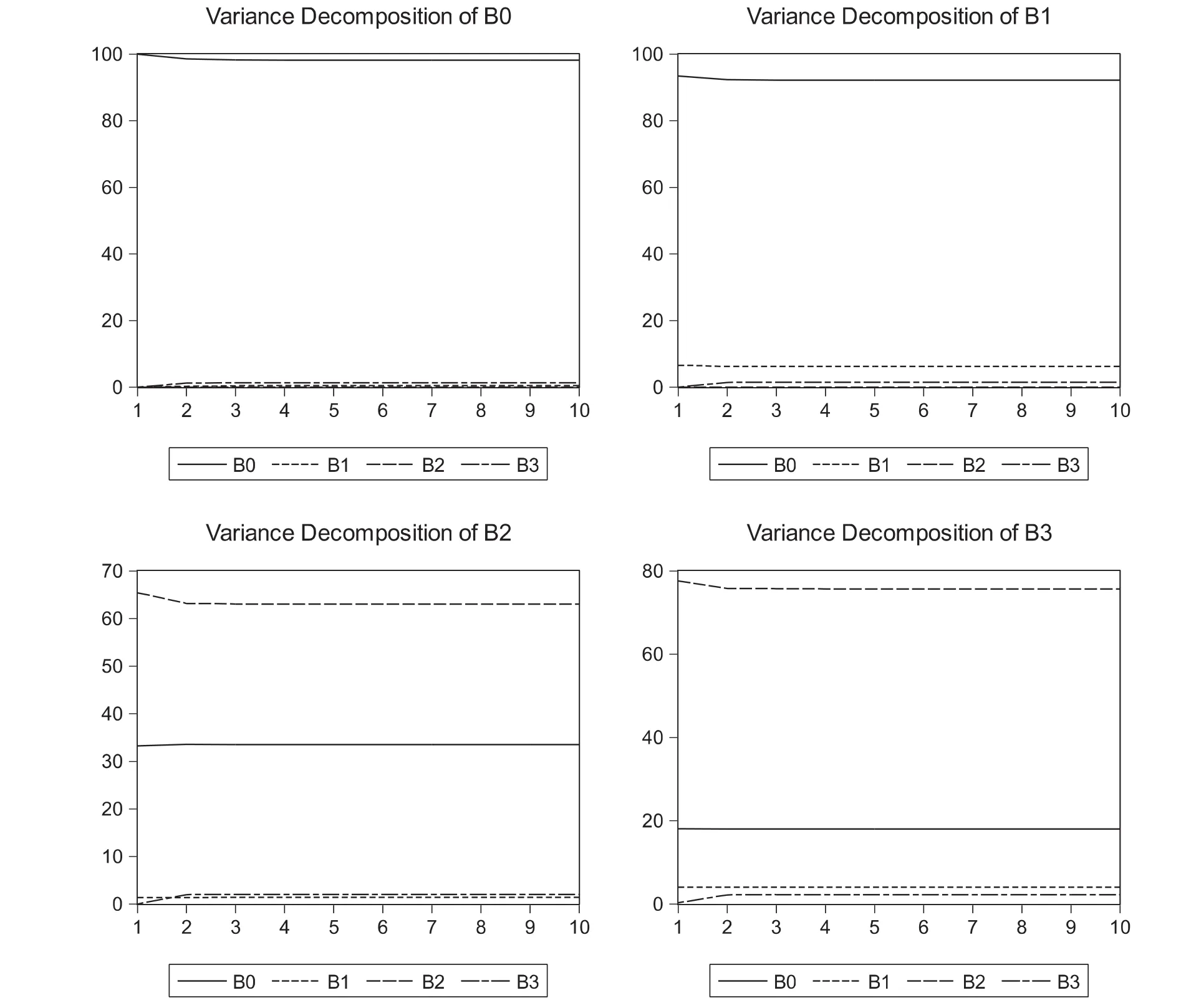
圖3 方差分解結果

對β2、β3進行向量自回歸，根據信息準則判斷滯后階數為0（AIC準則選取的是1）.如果按照滯后1階得到的VAR方程為：

再用新的VAR方程對2011年11月至2012年10月的參數值進行預測，該結果與四維向量自回歸的結果相比，β0、β1、β3預測偏差減小，β2預測偏差增大，預測符號都是正確的，但在第一期之后沒有根本性的改良.

鑒于VAR模型無法準確預測樣本外參數，本文進一步推測 β0、β1、β2、β3之間或許某些因子只受自身影響，而某些只受其他因子影響.陳芳菲、沈長征②對 β 序列采用 AR（1）模型，對1天、30天、60天的步長預測較為接近，90天步長預測效果稍好；康書隆、王志強③的研究顯示β序列均服從一個一階分布滯后過程.本文試圖改用ARMA模型或分布滯后模型對 β0、β1、β2、β3進行預測.由圖 4確定p=1、q=1，對 ARMA（1，1）模型進行估計.擬合優度很低，R=0.082795，調整的擬合優度更低，R=0.059865，并且系數 t統計量都通不過檢驗.β1、β2、β3的自相關、偏自相關圖都表明沒有顯著的截尾現象，故不適合建立ARMA模型.對相關性高的變量進行Granger因果檢驗，檢驗結果表明變量兩兩之間都沒有顯著的因果關系，故也不適合建立分布滯后模型.

圖4 的自相關、偏自相關圖

5 總結

本文研究了NSS模型中影響利率期限結構的水平因子β0、斜度因子β1、曲度因子β2和曲度調整因子β3的聯系，研究發現：交易所國債四個參數β0、β1、β2、β3的時間序列很難協整，銀行間國債四個參數的時間序列容易呈現平穩性，使用銀行間國債數據更能方便地分析時間序列的動態特征；樣本內 β0、β1、β2、β3序列間相關性非常高，β0序列內存在一階自相關，而β1、β2、β3序列內無自相關性；可以用VAR（1）建立時間序列模型，但是模型擬合優度非常低；脈沖響應檢驗表明β0對β1、β2的沖擊反應顯著，β2對β3的沖擊反應顯著；方差分解檢驗表明β0的變動基本不受其他參數影響，β1的變動主要受 β0的影響，β3的變動主要受 β2的影響；但Granger因果檢驗表明變量兩兩之間都沒有顯著的因果關系；在本文中，VAR（1）模型不適合樣本外預測.從理論上講，β0可以代表長期利率、-β1可以代表長短期利差，β1受 β0的影響較大，β2、β3均與中期利率有關，由于中長期利率受短期利率的直接影響，β0、β2、β3應該會受到 β1的影響.脈沖響應檢驗、方差分解檢驗與Granger因果檢驗得出的結論互相矛盾，原因可能是VAR（1）模型的擬合優度過低，沒有真實反映樣本數據的性質，而且也導致了預測結果幾乎沒有可信度.

注釋：

①胡志強，王婷.基于Nelson-Siege模型的國債利率期限結構預測[J].經濟評論，2009（6）.

②陳芳菲，沈長征.Nelson-Siege模型與國債收益率曲線的預測[J].統計與決策，2006（2）.

③康書隆，王志強.中國國債利率期限結構的風險特征及其內含信息研究[J].世界經濟，2010年（7）.

〔1〕陳芳菲，沈長征.Nelson-Siege模型與國債收益率曲線的預測[J].統計與決策，2006(2):133-135.

〔2〕胡志強，王婷.基于Nelson-Siege模型的國債利率期限結構預測[J].經濟評論，2009(6):57-66.

〔3〕康書隆，王志強.中國國債利率期限結構的風險特征及其內含信息研究 [J].世界經濟，2010(7):121-143.

〔4〕楊展，樊勝.貨幣政策對我國銀行間國債市場利率期限結構的影響——基于Nelson-Siege模型的實證分析[J].武漢金融，2012(8):18-21.

〔5〕胡永宏，李麗，常紅旭.利率期限結構與宏觀經濟變量的相互關系研究 [J].數理統計與管理，2012(9):871-879.