基于模糊學(xué)分析框架的翻譯標(biāo)準(zhǔn)研究

李 平

(安徽冶金科技職業(yè)學(xué)院 安徽馬鞍山 243000)

“忠實或信”是翻譯中的最重要的標(biāo)準(zhǔn)(當(dāng)然，表述翻譯標(biāo)準(zhǔn)的還有其他術(shù)語，如“化境”、“功能對等”等等)，它既是譯者在具體翻譯過程中時時要面對的問題，也是翻譯研究者們經(jīng)常探討和引起爭論的問題，也正是有這樣的問題才不斷地推動著翻譯的發(fā)展和翻譯理論的建設(shè)。漫長的翻譯歷史和同樣漫長的翻譯研究史使得圍繞“忠實或信”的話語綿延不斷，尤其是以經(jīng)驗和思辨為特點的傳統(tǒng)翻譯和譯論幾乎就很自然地把“忠實或信”當(dāng)作翻譯的出發(fā)點和歸宿點。

隨著翻譯研究的跨學(xué)科發(fā)展以及譯學(xué)本身的縱深發(fā)展，使得翻譯研究中的各種學(xué)科知識和各種研究方法的運用愈加廣泛，其中就包括以數(shù)理邏輯和觀察實驗為基礎(chǔ)的科學(xué)實證方法。本文嘗試將“忠實或信”中的主觀定義、描述模糊和寬泛納入模糊數(shù)學(xué)或模糊學(xué)(Fuzzy Mathematics)數(shù)理邏輯分析框架中，嘗試給出具有客觀性的定義和描述。希望拋磚引玉，賜教與各位同仁。

1 關(guān)于“忠實”、“信”標(biāo)準(zhǔn)的模糊性問題

我們在運用模糊數(shù)學(xué)討論忠實、信的模糊性之前，先介紹一下模糊數(shù)學(xué)和模糊性。

以精確數(shù)學(xué)及隨機數(shù)學(xué)為基礎(chǔ)的近代和現(xiàn)代科學(xué)技術(shù)最顯著的特點之一就是能非常有效地定義和描述客觀世界中那些界限分明的清晰事物，并能作出非此即彼的判斷和進行精確測量。但是，在客觀世界中還普遍存在著大量的模糊現(xiàn)象。比如，在日常生活中，經(jīng)常遇到許多模糊事物，沒有分明的數(shù)量界限，要使用一些模糊的詞句來形容、描述。如比較年輕、高個、大胖子、好、漂亮、善、熱、遠……。再如在翻譯學(xué)這樣的人文學(xué)科中的一些術(shù)語概念往往是非數(shù)值的，象“忠實”、“通順”、“信、達、雅”本質(zhì)上不能象物理量那樣實地測量。所以，以精確數(shù)學(xué)及隨機數(shù)學(xué)為主的傳統(tǒng)數(shù)學(xué)無法滿足人文、社會學(xué)科及其它“軟科學(xué)”的數(shù)學(xué)化、定量化趨向。

模糊數(shù)學(xué)作為專門描述和處理模糊性的理論和方法，我們首先要理解的一個基本概念，就是模糊性這個概念。為了識別事物，人們總要依據(jù)一定的標(biāo)準(zhǔn)對它們進行分類。在現(xiàn)實世界中，有許多事物可以依據(jù)精確的標(biāo)準(zhǔn)把事物分為彼此界限分明的類別，每個事物要么屬于某一類，要么不屬于該類，非此即彼，明確肯定，如“地球是行星”，“石頭不是食物”，“翻譯學(xué)是一門既包含藝術(shù)又包含科學(xué)的學(xué)科”，“這一句是直譯”，都是關(guān)于事物類屬的明確斷言，我們通常把這類事物稱為清晰事物。但是現(xiàn)實世界中還有許多事物和現(xiàn)象我們無法找到精確的分類標(biāo)準(zhǔn)，很難對某一事物是否屬于某一類作出明確肯定的斷言，如高山、大河，如譯論中的忠實、叛逆、通順、直譯、意譯、歸化、異化等。由于這些事物和現(xiàn)象從屬于某一類到不屬于該類是逐步過渡而非突然改變的，不同類別之間不存在截然分明的界限，因而不同的人對同一事物或現(xiàn)象可能作出不同的歸類。我們把事物或現(xiàn)象具有這種類屬的不清晰性稱為模糊性。

了解了模糊性，我們就可以來討論翻譯標(biāo)準(zhǔn)里的“忠實或信”的模糊性問題。我們知道翻譯就是把用一種語言文字表達的思想、內(nèi)容用另一種語言文字傳遞和表達出來。按照今天的人文學(xué)話語，傳遞和表達必須要做到“忠實而流暢地傳遞表達”或“取信于原文的傳遞和表達”。那么，做到如何“忠實”、“信”?這就大有文章可做了，從古人到今天，我們一直在絞盡腦汁，窮盡皓首地做這樣的文章，可一直做不到百分之百的“忠實”、“信”。我們無論是翻譯還是教授翻譯時，都會自覺或不自覺地使用到“忠實”、“信”這樣的標(biāo)準(zhǔn)，否則就不能稱之為翻譯了或翻譯學(xué)了。

根據(jù)王東風(fēng)看法(王東風(fēng)，2004/6:9)，“忠實”、“信”在本質(zhì)上是一個倫理二元對立的概念，要么忠，要么不忠，要么信，要么不信，不存在模糊的中間狀態(tài)，其實，從模糊學(xué)看，“忠實”、“信”就象“漂亮女人類”一樣缺乏明確的類別隸屬判據(jù)，到底什么才算“忠實”，什么才算“信”沒有明確、清晰的界限，在類別隸屬判據(jù)上存在著中間狀態(tài)、區(qū)別程度、等級對象等，也就是說“忠實”、“信”具有模糊性。“忠實”、“信”這種模糊性是來自事物性態(tài)和類屬的不確定性、不清晰性和漸變性，而這恰恰反映了世界的多樣性、多元性和差異性。“忠實”、“信”在譯學(xué)研究中缺乏觀察、描述和解釋的充分性就在于把“忠實”、“信”當(dāng)作了要么忠，要么不忠，要么信，要么不信這樣一個二值邏輯看待。我們知道，傳統(tǒng)的思維邏輯基礎(chǔ)是二值邏輯，要求對每個命題做出要么真、要么假的明確斷定。這是適于處理清晰概念和命題的邏輯模式。當(dāng)它用于處理模糊概念和命題時，理論上將導(dǎo)致邏輯悖論。根據(jù)邏輯學(xué)中最著名的禿頭悖論［1］，忠實與不忠實，信與不信同禿與不禿，年輕與年老一樣，這些概念都有模糊性，用精確的二值邏輯描述這類概念和用這類概念構(gòu)成的判斷和推理，必然導(dǎo)致忠實是不忠實、不忠實是忠實、信是不信、不信是信的悖論。

作為一個概念和術(shù)語，“忠實或信”的模糊性源于其考察對象在性態(tài)和類屬方面的亦此亦彼性，即具有中介過度性，也就是說“忠實或信”不再象以前那樣具有清晰性，即不是忠就是不忠那樣的非此即彼性，而是忠和不忠之間存在著許多中介過度態(tài)，即存在著許多程度不同，資格不同忠，而這許多忠的類屬是不確定的，在翻譯的某一方面、某一階段表現(xiàn)為不忠，但到了另一方面、另一階段就表現(xiàn)為忠。因此，原來對立的兩極“忠”與“不忠”變成互相滲透、互相貫通，由一極到另一極之間呈現(xiàn)出一系列中介過度狀態(tài)、環(huán)節(jié)或階段。由此看到，所謂清晰性是相對的，而模糊性卻是絕對的。我們以前用“忠實或信”標(biāo)準(zhǔn)來考察翻譯研究中的對象，是把考察對象所包含的差異忽略不計就可能成為清晰，而現(xiàn)在用“忠實或信”來考察時，其對象所包含的差異就不能忽略不計，這時就可能形成模糊性，我們要通過了解“忠實或信”的這種差異和變化來把握所考察對象自身的同一性，比如，把“舉筷”譯為“to take up the chopsticks to eat”或譯為“to take up a knife and fork”，把“firewall”譯為“網(wǎng)絡(luò)安全通路”或譯為“防火墻”，都屬于忠實或信，即譯論里常講的異化、歸化以及直譯、意譯，或者更嚴(yán)格講就是屬于“忠實或信”的模糊性。

2 “忠實”或“信”的一個模糊學(xué)分析框架

要給“忠實”或“信”以適當(dāng)?shù)哪：龑W(xué)描述，首先需要介紹一下集合的概念，通俗地說，所謂集合，就是把一些事物匯集到一起組成一個整體，匯集在一起的事物就是這個集合的元素或成員，例如教室內(nèi)的桌椅，圖書館的全部藏書的集合。通常集合用大寫字母A、B、X、Y等來表示，元素用小寫字母a、b、x、y等來表示。x屬于A，記為x∈A;y不屬于A，記為y?A。由于在經(jīng)典集合論中，集合被理解為人們直觀上或思想上的那些確定的、能夠彼此區(qū)分的事物匯集在一起形成的整體，所以集合也常用特征函數(shù)來表示。設(shè)集合A的特征函數(shù)，記為fA(x)，定義為:

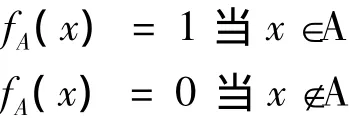
顯然我們可以用集合論的數(shù)學(xué)模型來描述我們精確二值邏輯:對于任一元素x和集合A，要么x∈A，要么x?A，二者必居其一且只居其一。這就是經(jīng)典集合論對清晰事物類屬關(guān)系的二值的、絕對的規(guī)定，如傳統(tǒng)譯論中的不是忠實就是不忠實這樣非此即彼的二值邏輯思維。然而，經(jīng)典集合論卻無法描述類屬不分明的模糊事物，于是就有了查德(Zedeh)把經(jīng)典集合推廣到模糊集合，這意味著把元素屬于集合的概念模糊化，承認(rèn)所考察的對象存在既非完全屬于某集合，又非完全不屬于該集合的元素，變絕對的屬于概念為相對的屬于概念。這樣，不同元素對同一集合有不同的隸屬程度。所以，在模糊集合中，給定范圍內(nèi)元素對它的隸屬關(guān)系不一定只有“是”或“否”兩種情況，而是用介于0和1之間的實數(shù)來表示隸屬程度，存在許多中間過渡狀態(tài)。比如“老人”是個模糊概念，70歲的肯定屬于老人，它的從屬程度是1，40歲的人肯定不算老人，它的從屬程度為0，按照查德給出的公式，55歲屬于“老”的程度為0.5，即“半老”，60歲屬于“老”的程度0.8。查德認(rèn)為，指明各個元素的隸屬集合，就等于指定了一個集合。當(dāng)隸屬于0和1之間值時，就是模糊集合。

有了模糊集合，我們可以對“忠實”或“信”作出描述和解釋。根據(jù)模糊學(xué)，翻譯研究中的“忠實”或“信”實際上可以看作是一個模糊集合:完全忠、十分忠、很忠、忠、相當(dāng)忠、有些忠、有點忠、不太忠、不很忠、不忠、根本不忠等等，當(dāng)然這是比較通俗說法。對忠實或信的模糊集合比較嚴(yán)格的描述如下:

設(shè)A是論域U上的模糊集合(所謂論域是指討論涉及的對象范圍)，也就是在“忠實”或“信”這個翻譯標(biāo)準(zhǔn)論域上，“忠實或信”的模糊集合是用A來表示的，在論域中百分之百的忠實或信屬于A的元素對A的隸屬度為μ=1，百分之百的不忠實或信不屬于A的元素對A的隸屬度為μ=0，其余的元素對A的隸屬度用介于0和1之間的實數(shù)μ來表示，較大的μ值表示較高的忠實或信的隸屬度，這樣，“忠實或信”的模糊集合A就得到一種定量的描述。

以“～”作為模糊化記號，模糊集合記為A、B、C、等。我們給出如下定義:譯論域U上的“忠實”或“信”的模糊集合A是用一個從U到實區(qū)間［0，1］的函數(shù)μA來描述的，μA叫做模糊集合A的隸屬函數(shù)②，函數(shù)值μA(x)代表元素x對集合A的隸屬度。

對照經(jīng)典集合，可以看到經(jīng)典集合用特征函數(shù)描述，那么“忠實”或“信”特征函數(shù)值域為集合{0，1}這樣的要么忠實，要么叛逆的二值或二元對立邏輯推理，而模糊集合是用隸屬函數(shù)來描述的，隸屬函數(shù)的值域為區(qū)間［0，1］，也就是存在著不同資格、不同程度的連續(xù)過度的“忠實”或“信”，例如，把“轉(zhuǎn)首肯為搖頭”(邵志洪、岳俊，2005/1:74)譯為:

如果設(shè)U為該句的“忠實”或“信”，設(shè)A為U上的把“轉(zhuǎn)首肯為搖頭”譯成英語時“忠實”或“信”的模糊集合，我們得到如下隸屬函數(shù)或隸屬度μA(x):

x (1) (2) (3) (4)μA(x)1 0.8 0.7 0.5

所以，從“忠實”到“叛逆”之間存在著許多資格不同的忠實和叛逆這樣的元素，它們從屬于集合到不屬于集合的漸變過程，亦即忠實或信的隸屬度在“忠實”或“信”上存在著分布，這種分布反映出人們對“忠實”或“信”因不同原因或不同翻譯策略而有不同的認(rèn)知和理解，這不僅說明“忠實或信”的隸屬度具有客觀性和實證性，而且還有主觀性，因為“忠實或信”的隸屬度是一種非數(shù)值的量的規(guī)定性，不能象物理量那樣實地測量，要求象測量長度、高度那樣找到隸屬度的客觀標(biāo)準(zhǔn)，是不現(xiàn)實的，實際給出的隸屬度總有一定的主觀成分，不同的人對同一事物隸屬度的指定常有差別，令μA((1))=0.9而不是1也未嘗不可，即認(rèn)為(1)不是百分之百的忠實而是百分之九十的忠實，因為可能存在比“Nodding approval will give way to head-shaking.”忠實或信隸屬度更高的譯文;同樣，令μA((4))=0.3而不是0.5也意味著人們可能認(rèn)為“Positive views will give way to negative views.”忠實不足，而叛逆有余，即(4)不是百分之五十的忠實而是有百分之七十的叛逆。可見，隸屬度的這種不唯一性，是模糊性的一個特點，隸屬度中包含一定主觀成分給譯者、譯論者發(fā)揮主觀能動性提供了條件，這恰恰也是傳統(tǒng)譯論里常講到的翻譯需要創(chuàng)造性、藝術(shù)性、豐富的經(jīng)驗、熟練的技巧和靈活的策略的源泉，有了這些，才能給出切合實際的隸屬函數(shù)，才能應(yīng)用模糊學(xué)方法嘗試在科學(xué)上對“忠實”或“信”作具體的定量分析和實證研究，我們的主觀性就有了客觀依據(jù)，從這種意義上講，翻譯研究也有了實證研究的意義。

3 結(jié)語

長期以來，“忠實”或“信”作為譯學(xué)中的術(shù)語和標(biāo)準(zhǔn)，一直用于譯學(xué)研究和探討，隨著譯學(xué)研究和探討的不斷發(fā)展，人們對“忠實”或“信”內(nèi)涵和外延認(rèn)識也在深入，把“忠實或信”放入模糊學(xué)分析框架，運用模糊集合對“忠實”或“信”作出定量分析，是我們的一個嘗試，通過這一嘗試，我們希望能對“忠實或信”這樣的標(biāo)準(zhǔn)上有更多的客觀的和實證的描述，隸屬函數(shù)的定量實證分析使得“忠實或信”這樣翻譯標(biāo)準(zhǔn)的主觀性、人文性的描述具備量化實證的客觀依據(jù)，從而有可能對翻譯標(biāo)準(zhǔn)作出科學(xué)的解釋和探索。

注釋:

①禿頭悖論:日常生活中，某人是否禿頭是容易判斷的。要給禿和不禿下精確定義，卻難乎其難。按照傳統(tǒng)邏輯，有兩種方案可供選擇:(1)承認(rèn)存在一個作為界限的頭發(fā)根數(shù)n 0，n即實際的頭發(fā)根數(shù)，規(guī)定n≤n 0時為禿頭，n＞n 0時為不禿。但一發(fā)之差便分禿與不禿，為常識所不容，這樣的n 0不存在。(2)承認(rèn)一發(fā)之差不改變禿與不禿，這似乎合乎常識。從常識看，命題A“比禿頭多一根頭發(fā)還是禿頭”，命題B“比非禿頭少一根頭發(fā)者還是非禿頭”，都是真命題。命題α“一發(fā)皆無(n=0)者是禿頭”，命題β“滿頭烏發(fā)者(例如n=1000000)是非禿頭”，顯然也都是真命題。但是，從命題A和命題α出發(fā)，按傳統(tǒng)邏輯的推理規(guī)則作連鎖推理，可以得出顯然為假的命題δ“滿頭烏發(fā)者是禿頭”;從命題B和命題β出發(fā)，又可推出顯然為假的命題ε“一發(fā)皆無者是非禿頭。這就導(dǎo)致了悖論。同樣可以出現(xiàn)年齡悖論:由顯然為真的命題“20歲的人是年輕人”和“比年輕人早生一日的人還是年輕人”可以推出顯然為假的命題“百歲老人是年輕人”。

②如讀者熟悉現(xiàn)代數(shù)學(xué)映射概念，就有以下更為嚴(yán)格的定義:

論域U到實區(qū)間［0，1］的任一映射

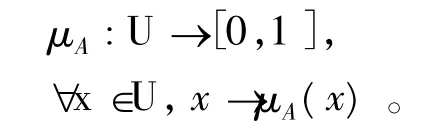
都確定U上的一個模糊集合A，μA叫做A的隸屬函數(shù)，μA(x)叫做x對A的隸屬度。

［1］樓世博，孫章，陳化成.模糊數(shù)學(xué)［M］.北京:科學(xué)出版社，1983

［2］左孝凌.離散數(shù)學(xué)［M］.北京:經(jīng)濟科學(xué)出版社，2000

［3］苗東升.模糊學(xué)導(dǎo)引［M］.北京:中國人民大學(xué)出版社，1987

［4］賀仲雄.模糊數(shù)學(xué)及其應(yīng)用［M］.天津:天津科學(xué)技術(shù)出版社，1983

［5］王東方.解構(gòu)“忠實“——翻譯神化的終結(jié)［J］.中國翻譯，2004.6

［6］司顯柱.譯作一定要忠實原作嗎?——翻譯本質(zhì)的再認(rèn)識［J］.上海科技翻譯，2002.4

［7］邵志洪，岳俊.英漢語篇銜接對比與翻譯策略［J］.中國翻譯，2005.1

［8］李平.翻譯學(xué)信息范式研究［J］.中國科技翻譯，2000.3

［9］Zadeh，L.A.Fuzzy Sets［J］Inf.Control，8(1965).

［10］Zadeh，L.A.Fuzzy Algorithms［J］Inf.Control，12(1968).

［11］Zadeh，L.A.A New Approach to System Analysis in Man and Computer［M］North-Holland，Amsterdam，1974.