圖像壓縮中基于分形維數的小波基選取

唐國維,王苫社,張 巖

(1.東北石油大學 計算機與信息技術學院,黑龍江 大慶 163318; 2.哈爾濱工業大學 計算機科學與技術學院,黑龍江 哈爾濱 150001)

圖像壓縮中基于分形維數的小波基選取

唐國維1,王苫社2,張 巖1

(1.東北石油大學 計算機與信息技術學院,黑龍江 大慶 163318; 2.哈爾濱工業大學 計算機科學與技術學院,黑龍江 哈爾濱 150001)

小波函數具有多樣性,采用不同的小波基對圖像進行壓縮后,重構圖像的質量有一定差別.為了選取合適的小波基對圖像進行小波變換編碼,提出一種基于分形維數的小波基選取的圖像壓縮方法.通過差分計盒法計算相關圖像的分形維數,將圖像按照分形維數數值的不同劃分為不同類別.選取每類中的代表圖像,采用多種小波基,分別用SPECK算法對其壓縮處理.根據重構圖像峰值信噪比的數值,得出每類圖像適合的小波基.實例分析表明,該方法可以在一定程度上提高小波圖像編碼的峰值信噪比.

圖像壓縮;小波基選取;小波變換;分形維數;編碼

0 引言

小波變換因其特有的與人眼視覺相符的多分辨率分析能力及方向選擇能力而被廣泛應用于圖像壓縮領域[1-4].在JPEG 2000標準中,將基于小波變換的EBCOT(可擴展圖像壓縮編碼)算法作為核心算法,表明小波變換已取代DCT(離散余弦變換)成為新一代圖像編碼的主要變換工具[5].由于不同的小波函數時頻局域特性不同,選用不同小波基將影響算法的編碼性能,因此選擇小波基是圖像壓縮中首要考慮問題.選擇小波基需要考慮小波函數的緊支集性、正交性、正則性和消失矩等方面,在實際應用中,編碼的壓縮比和恢復圖像質量更為重要.李戰明等[6]研究Daubechies正交和雙正交小波基,通過比較變換圖像的增益、熵、能量比和峰值信噪比等指標,認為雙正交小波基D9/7是一種較好的小波基,但沒有考慮不同類型圖像性質.Thakkar Falgun等[7]基于均方根誤差、相關系數和峰值信噪比,研究Haar、db4、bior6.8和sym2四種小波基的壓縮性能,認為Haar小波對醫學圖像壓縮具有優勢,而Sym2更適合自然圖像的壓縮,但其方法只根據圖像應用領域,而不是圖像自身特性研究適合的小波基,同時對圖像類型也考慮較少.Chopra Sanjeev[8]提出一種在5級小波分級下,根據壓縮比、能量比、均方誤差和峰值信噪比等性能參數確定最優小波基的算法,考慮壓縮圖像的各項參數,選取的小波基較為合理,但計算量過大,且只針對固定的5級分解進行.

鑒于分形與圖像灰度表示之間有一定對應關系,且是獨立于圖像一定范圍內分辨率比例而穩定存在的量,筆者將分形用于小波基選取,通過實驗分析分形維數和圖像灰度特性之間的內在聯系,確定適合對圖像進行壓縮處理的小波基.實驗結果表明,可以提高小波圖像編碼的整體效率.

1 圖像的分形維數

分形維數即分數維,是定量描述分形的基本參量,且為標度變換下的不變量.常用的分形維數包括豪斯多夫維、盒維及相似維等.其中,豪斯多夫維對任何集F都有定義,最為常用,但對其值的計算和估計有一定困難;盒維的計算和估計較為簡單,且與圖像紋理結構有密切關系,因此在實際應用中較為廣泛[9-10].

1.1 盒維

盒維由Bouligand于1929年引入,又稱Bouligand維.

定義1 設集合F?Rn,記Nε(F)是可以覆蓋F的、邊長為ε的n維立方體的最少個數,則F的盒維DB定義為

如果集F具有“自相似”的子集,而這些子集又依次具有相同比例的子子集.設母集F有N 個子集,而每一個子集中各點間的距離按因子1/r增大時,都恒等于該母集.如果規定初始尺度為1,并取邊長ε=rk,則覆蓋F所需的立方體的個數Nε(F)=Nk,可知:

式中:N為由前一個母集按r比例縮小后的子集個數.

1.2 圖像的分形維數

二維灰度圖像可以被看作是1個三維空間中的曲面,圖像的灰度變化表示該曲面的崎嶇程度,當用不同尺度測量該曲面時,得到的維數就是圖像的分形維數.計算分形維數的方法包括ε-毯子法、差分計盒法、基于數學形態學的方法等,其中差分計盒法[11]對粗糙度小的紋理比較敏感,且計算簡單,因此采用該方法計算圖像的分形維數.

對于一幅N×N的二維灰度圖像,將其劃分為s×s的子塊(1＜s＜N/2,s∈Z+).令r=s/N,并假定圖像灰度在第(i,j)網格中的最小值和最大值分別落在第k和第l個盒子中,nr(i,j)是覆蓋第(i,j)網格中的圖像所需的盒子數,Nr是覆蓋整個圖像所需的盒子數,則圖像的分形維數Df可表示為

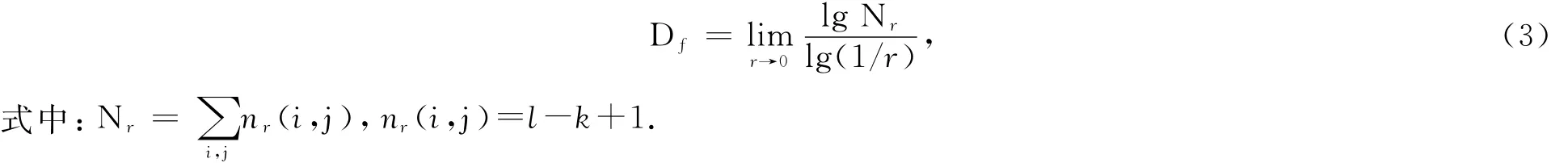
針對不同的r計算Nr,應用最小二乘法即可求得圖像的分形維數.

2 基于分形維數的小波基選取

分形維數具有標度變換下的不變性,即不同圖像的分形維數不同,相似圖像的分形維數值必然接近.選取若干幅在圖像編碼中常用的典型圖像[12],按文中方法分別計算分形維數,結果見表1.

表1 不同圖像的分形維數Table 1 The fractal dimension of different images

由表1可以看出,不同圖像的分形維數不同,主要反映圖像紋理/邊緣等灰度特性的差異.結合圖像本身特性,將圖像按照分形維數值分為5類(見表2).

表2 基于分形維數的圖像分類Table 2 Based on the fractal dimension of image classification

為研究5類圖像在不同小波基下的壓縮效果,文中選用SPECK(Set Partitioned Embedded Block Co-der,集合分裂嵌入塊編碼)圖像壓縮算法[13-14],分別進行圖像壓縮實驗.SPECK算法是一種基于塊結構的編碼方法,與其他編碼算法相比有獨特優勢:(1)塊間可以獨立編碼,所需動態存儲空間更小;(2)該算法容錯性更高,當傳輸發生誤碼時,只有誤碼的塊會受到影響,不會影響其他塊.

在基于小波的圖像壓縮中,常用的小波函數包括Haar、db系列、sym系列、coif系列、bior系列等[12].從5類圖像中各選取1幅代表圖像,基于不同的小波基,采用SPECK算法進行壓縮和解壓縮實驗,碼率為0.2 bpp時,PSNR(Peak Signal to Noise Ratio,峰值信噪比)見表3.

表3 不同小波基下各類圖像的PSNRTable 3 All kinds of image PSNR under different wavelet base

由表3可以看出,采用不同的小波基,同一幅圖像的PSNR相差很大,表明對不同類型圖像,應選取不同的小波基進行壓縮以獲得更好的壓縮性能.因此,基于PSNR最大化原則,根據表3歸納出適合不同類型圖像壓縮的小波基(見表4).

表4 基于分形維數的小波基選擇Table 4 Based on the fractal dimension of wavelet base selection

3 小波基選取實例

按照式(3)計算待壓縮圖像的分形維數,然后根據計算結果查表4,選取適合對該圖像壓縮的小波基,進而選擇相應壓縮算法對圖像進行壓縮處理.為驗證文中基于分形維數小波基選擇的有效性,選取2幅樣本以外的圖像進行實驗,大小為512×512(見圖1).

經計算得到2幅圖像的分形維數分別為0.866 0和0.874 2,分別屬于class 3和class 4類圖像(見表2).根據表4,分別選擇bior 4.4和coif 5小波基.為進一步說明算法的性能,采用SPECK算法對圖像進行壓縮處理,并將壓縮后的PSNR與基于sym 8小波基的進行比較(見表5).由表5可以看出,采用文中算法選取的小波基進行壓縮,獲得更好的壓縮性能.碼率為0.25 bpp時重構圖像的效果見圖2.由圖2可以看出,在壓縮比為32倍時,圖像壓縮效果較為滿意.

圖1 小波基選取示例圖像Fig.1 The selection of wavelet base sample image

表5 不同小波基下2幅示例圖像的PSNRTable 5 Under different wavelet base 2 sample images PSNR

圖2 2幅示例圖像壓縮后的重構效果Fig.2 2 after the example images compression effect of refactoring

4 結束語

在基于小波變換的圖像編碼壓縮中,采用一種小波基不能滿足任意圖像的壓縮效果,需要根據圖像本身特性選擇合適的小波基.通過分析分形維數和圖像紋理/邊緣特性之間的關系,基于盒維并采用差分計盒法計算圖像的分形維數,進而提出一種基于分形維數的小波基選取算法:對于任意一幅圖像,計算得到該圖像的分形維數,按照圖像自身特征和分形維數選擇合適的小波基,并對圖像進行壓縮處理.該算法降低小波基選取的盲目性,具有一定的實用價值.

[1] Cui Yueli,Chen Zhigang,Chen Aihua.Research and progress of image compression coding based on wavelet[C]//ICMENS2011.USA:TTP Publisher,2011:1352-1355.

[2] Beladgham M,Bessaid A,Taleb-Ahmed A.Medical image compression using quincunx wavelets and SPIHT coding[J].Journal of E-lectrical Engineering and Technology,2012,7(2):264-272.

[3] Elamaran V,Praveen A.Comparison of DCT and wavelets in image coding[C]//ICCCI 2012.USA:IEEE Publisher,2012:1-4.

[4] Liu Weidong,Feng Guiliang,Li Zhonghua.Optimization on wavelet SPECK image coding algorithm[C]//IBI 2011.Berlin Heidel-berg:Springer-Verlag Publisher,2011:693-699.

[5] Taubman D S,Marcellin M W.JPEG2000 Image Compression Fundamentals,Standards and Practice[M].Boston:Kluwer Academic Publisher,2002:231-235.

[6] 李戰明,遲洋.圖像壓縮中小波基的選擇研究[J].機械與電子,2009,9(24):18-21.

Li Zhanming,Chi Yang.Research on wavelet bases selection for image compression[J].Machinery&Electronics,2009,9(24):18-21.

[7] Thakkar Falgun,Kher Rahul,Modi Chintan.Selecting most favorable basis function for compressing natural and medical images using wavelet transform coding[C]//IPCV 2009.Las Vegas:CSREA Press,2009:1042-1058.

[8] Chopra Sanjeev,Kaur Harmanp,Kaur Amandeep.Selection of best wavelet basis for image compression at decomposition level 5[C]//ICCTD 2010.USA:IEEE Publisher,2010:442-445.

[9] Falconer K J.Fractal Geometry:Mathematical foundations and applications[M].曾文曲,等譯.沈陽:東北工學院出版社,1991:102-140.

[10] 陳守吉,張立明.分形與圖像壓縮[M].上海:上海科技教育出版社,1998:45-90.

Chen Shoujie,Zhang Liming.Fractal and image compression[M].Shanghai:Shanghai Scientific and Technological Education Publishing House,1998:45-90.

[11] Harrouni S.New method for estimating the fractal dimension of discrete temporal signals[J].IEEE International Symposium on Industrial Electronics,2008:2497-2502.

[12] 王苫社.基于小波及分形的嵌入式圖像編碼算法研究[D].大慶:大慶石油學院,2010.

Wang Shanshe.Research on embedded image coding algorithm based on wavelet and fractal[D].Daqing:Daqing Petroleum Institute,2010.

[13] Islam A,Pearlman W A.An embedded and efficient low-complexity hierarchical image coder[A].Visual Communications and Image Processing'99[C].San Jose:SPIE Publisher,1999:294-305.

[14] Pearlman W A,Islam A,Nagaraj N.Efficient,low-complexity image coding with a set-partitioning embedded block coder[J].IEEE Transactions on Circuits and Systems for Video Technology,2004,14(11):1219-1235.

TP391.41

A

2095- 4107(2014)01- 0112- 04

2013- 12- 19;編輯:張兆虹

黑龍江省教育廳科學技術研究項目(12521050);中國石油科技創新基金研究項目(2012D-5006-0609)

唐國維(1966-),男,博士,教授,主要從事圖像與視頻編碼、焊縫缺陷檢測與識別等方面的研究.

DOI 10.3969/j.issn.2095-4107.2014.01.017