鋼框架十字型剛性節點滯回性能分析與設計

計 靜,邢 菲,武英杰,張文福,袁朝慶,張 丹,杜 娟

(1.黑龍江省防災減災工程與防護工程高校重點實驗室 東北石油大學土木建筑工程學院,黑龍江 大慶 163318; 2.大慶石化工程有限公司,黑龍江 大慶 163714)

鋼框架十字型剛性節點滯回性能分析與設計

計 靜1,邢 菲1,武英杰2,張文福1,袁朝慶1,張 丹1,杜 娟1

(1.黑龍江省防災減災工程與防護工程高校重點實驗室 東北石油大學土木建筑工程學院,黑龍江 大慶 163318; 2.大慶石化工程有限公司,黑龍江 大慶 163714)

為研究鋼框架十字型剛性節點構件的滯回性能,以軸壓比、H型鋼柱腹板厚度、鋼梁截面形式及加勁肋為參數,設計8組鋼框架十字型剛性節點和1組T型剛性節點;基于簡化的力學模型和材料的本構關系,利用ABAQUS軟件建立有限元模型,分析節點試件的滯回性能;通過與已有的T型剛性節點試驗結果對比,兩者吻合較好,驗證有限元模型的合理性.開展十字型節點仿真分析,提取節點荷載—位移滯回曲線、包絡圖、骨架曲線和應力云圖,獲得柱軸壓比、H型鋼柱腹板厚度、鋼梁截面形式及加勁肋對該類節點抗震性能的影響規律,并對軸壓比、柱腹板與翼緣厚度比提出設計建議.結果表明:柱軸壓比設計限值建議取為0.5,柱腹板與翼緣厚度比設計限值建議取為0.75.當截面形式為H型鋼時,十字型剛性節點的抗震性能良好,并且優于截面形式為鋼管的,節點域設置橫向加勁肋可有效提高節點的抗震性能.

十字型剛性節點;滯回性能;有限元分析;T型節點;抗震性能;橫向加勁肋;抗震設計

0 引言

鋼結構以自重輕、強度高、延性好、抗震性能優越和布局靈活等優點在土木工程結構中被廣泛應用[1-5].近年來,鋼框架與壓型鋼板混凝土組合樓板的結合使鋼結構在高層建筑中應用的越來越多,已成為主要的建筑結構體系.鋼結構本身具有一定的特殊性,鋼框架節點的力學性能直接影響鋼結構的安全性和適用性,因此確保結構節點有較好的抗震能力是鋼結構設計的關鍵.

人們對不同的節點形式開展試驗研究和理論分析,劉燕[6]等通過在梁腹板上開洞,分析削弱型節點的滯回性能,結果表明梁腹板削弱型節點塑性變形能力較好,能有效減小梁翼緣處的應力.戴紹斌[7]等對翼緣削弱型剛性連接節點進行低周反復荷載作用下試驗研究和非線性有限元分析,結果表明翼緣削弱型剛性連接節點具有較大的連接剛度和理想的耗能性能,梁翼緣處的焊縫強度是影響翼緣削弱型剛性連接節點性能的主要因素.王秀麗等對鋼框架梁腹板開孔型連接節點力學性能開展試驗研究,探討梁柱節點域滯回性能,利用ABAQUS有限元軟件探討不同塑性鉸位置對結構延性的影響,結果表明可降低連接焊縫脆性破壞的可能性,有效控制塑性鉸的位置,從而改善框架結構的整體延性[8].陳宏等針對4種構造形式的鋼框架梁柱節點進行非線性有限元分析,將節點的力學性能與試驗結果進行對比,結果表明吻合良好,并提出改進型節點形式[9].人們也開展樓板和墻體對剛性節點力學性能的影響分析研究,考慮組合效應后節點的剛度和承載力得到提高,滯回性能和抗震能力得到改善[10-15].

為研究不同構造對鋼框架端板連接半剛性節點受力性能的影響,石永久等[13]開展鋼框架端板連接半剛性節點受力性能分析,探討鋼框架端板連接半剛性節點的受力性能,結果表明平齊式端板連接的特性更接近于鉸接節點,承載力和剛度降低近50%,而外伸端板采用加勁肋后,可以使節點獲得良好受力性能.Jun Jin[14]開展T型剛性節點擬靜力試驗研究,得到T型節點彎矩—轉角關系曲線,提出節點的抗震設計方法,結論具有一定的局限性.

盡管對不同節點的研究較多,但對實際工程提出可操作性的設計建議較少,針對軸壓比、H型鋼柱腹板厚度、鋼梁截面形式及加勁肋對鋼框架十字型剛性節點滯回性能的數值分析尚未見報道.筆者采用ABAQUS有限元軟件[15-16]開展8組鋼框架十字型剛性節點和1組T型節點的滯回性能分析,考察不同參數對十字型節點力學性能的影響,探索試件的剛度退化、耗能能力、承載力和延性等抗震性能指標,提出對實際工程具有可操作性的設計建議,為該類節點的設計提供依據,為開展鋼混凝土組合結構節點的抗震性能試驗提供指導.

1 試件設計

為考察軸壓比、H型鋼柱腹板厚度、鋼梁截面形式及加勁肋參數對十字型節點抗震性能的影響,基于GB 50017-2012《鋼結構設計規范》,設計8組不同參數控制下的十字型剛性焊接節點,試件參數見表1.

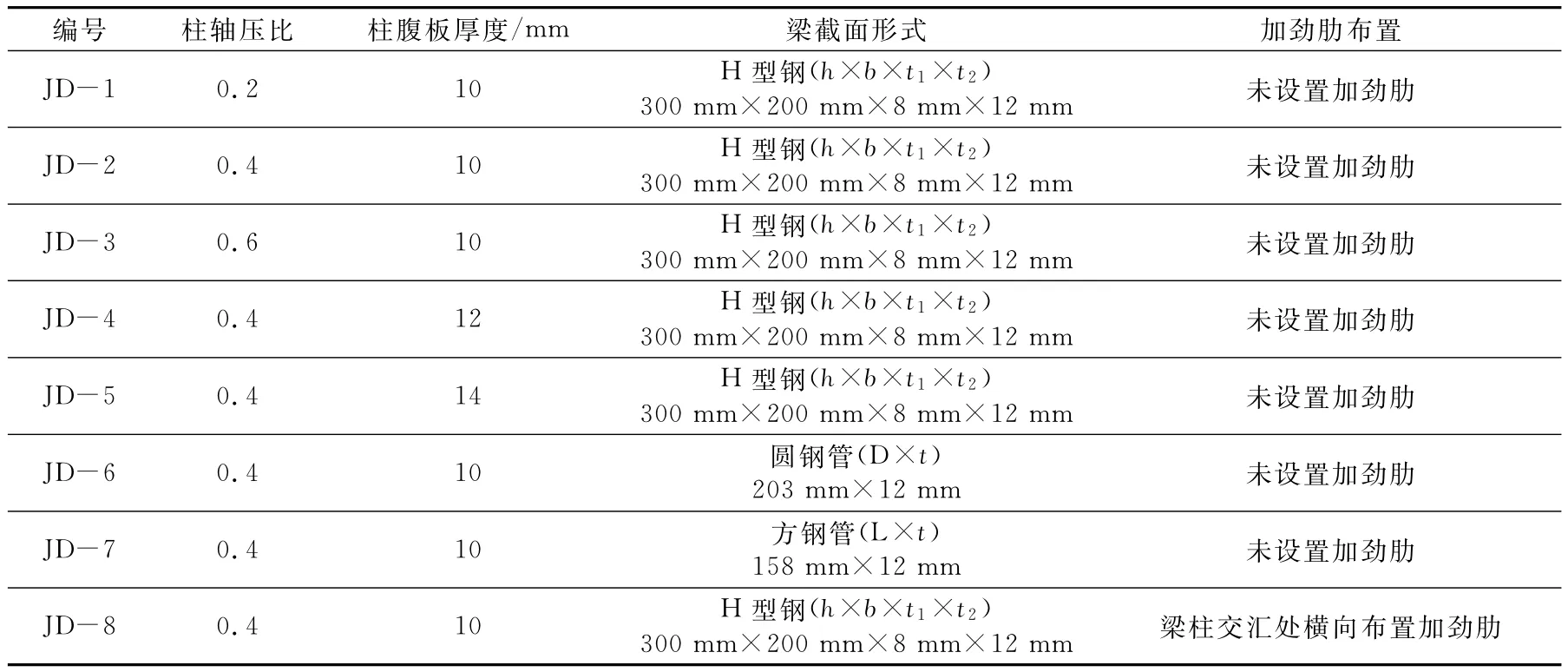
表1 試件主要參數Table 1 The main parameters of specimens

以節點試件JD-2作為標準試件,柱截面尺寸為400 mm×300 mm×10 mm×16 mm,高度為3 000 mm;H型鋼梁截面尺寸為300 mm×200 mm×8 mm×12 mm,長度為1 500 mm.試件變化參數為軸壓比、H型鋼柱腹板厚度、鋼梁截面形式及有無加勁肋.軸壓比分別為0.2、0.4、0.6,H型鋼柱腹板厚度分別為10、12、14 mm;以梁柱接觸面積為定值,改變梁截面形式,梁截面分別取為H型鋼、圓鋼管、方鋼管;柱腹板橫向加勁肋設置在梁柱交匯處,尺寸為368 mm×145 mm×12 mm.部分試件三維幾何模型見圖1.同時,設計一組T型剛性節點試件,編號為EERC-PN1,尺寸和力學性能見表2,其中尺寸、截面形式與文獻[14]的試驗節點完全相同,用于驗證有限元模型分析的正確性.為方便應用和計算,將文獻[14]采用的英制單位轉換為國際單位制.

圖1 節點三維幾何實體模型Fig.1 Three-dimensional geometry entity model of nodes

表2 EERC—PN1試件尺寸及力學性能Table 2 EERC—PN1 component size and mechanical properties

2 ABAQUS有限元建模

2.1 簡化力學模型

十字型和T型節點簡化力學模型見圖2,其中N為作用在柱上的恒定軸力;P為施加在梁端的反復低周荷載.框架梁柱交匯形成節點,節點受力比較復雜,將框架柱取上下柱各一半,兩端形成鉸支座,下端約束水平X、豎向Y方向的位移,上端約束水平X方向位移,構件可以轉動,在柱頂施加恒定軸力.框架梁兩端各取一半,形成自由端,施加反復荷載.

圖2 節點簡化力學模型Fig.2 Simplified mechanical model of nodes

2.2 鋼材本構模型

鋼材采用Q345鋼,力學性能見表3.考慮節點滯回分析發生的位移較大,鋼材屈服后進入強化階段,應力隨著應變的增加而增大,因此鋼材本構模型采用雙線性隨動強化模型,強化階段斜率取為0.05Es(Es為彈性模量),簡化的應力—應變關系曲線見圖3,其中fy為屈服強度.

表3 鋼材力學性能Table 3 Mechanical index of steel

2.3 有限元模型

2.3.1 單元選取與整體節點形成

采用ABAQUS有限元軟件[15-16]進行節點滯回非線性分析,其中H型鋼柱、H型鋼梁、圓鋼管、方鋼管、加勁肋及墊板采用8節點線性減縮積分格式的三維實體單元C3D8R建立,為使鋼管受力均勻,在圓鋼管梁端部布置剛性墊板.在裝配功能模塊中創建梁、柱、墊板部件,將各部件裝配起來,各部件間采用“綁定”的方式接觸;該類約束允許綁定兩個網格劃分完全不同的區域,且綁定后的部件間不發生相對運動.

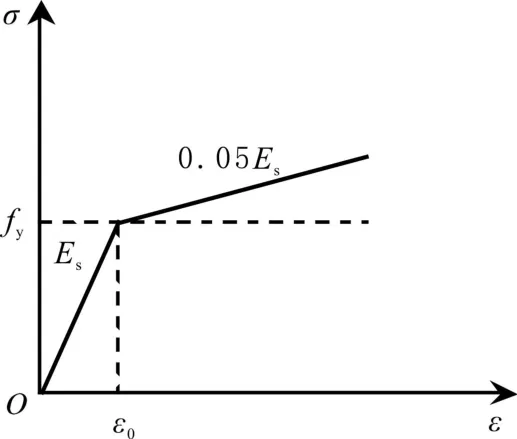
圖3 鋼材應力—應變關系曲線Fig.3 The stress-strain curve of steel

2.3.2 節點網格劃分

結合十字型節點模型的特點,采用掃掠網格劃分技術對建立的非獨立實體相對應的部件進行網格劃分,得到相對較容易收斂的六面體單元.不同截面形式的梁構成的節點劃分網格后的有限元模型見圖4.

圖4 節點有限元模型Fig.4 Finite element models of nodes

2.3.3 邊界約束與荷載施加

結合十字型節點的受力特點,將節點有限元模型柱底和柱頂的U1、U2、UR2、UR3自由度進行約束,即形成鉸接約束.加載方式采用擬靜力加載方式,首先根據軸壓比計算軸向壓力,將軸向壓力以面荷載的形式施加在柱頂,在后續分析中保持軸向壓力不變;然后采用位移約束方式分別在梁端施加反復位移荷載,加載方案見圖5,其中δ為位移加載量,n為加載循環次數.施加邊界約束與荷載后的有限元模型見圖6.

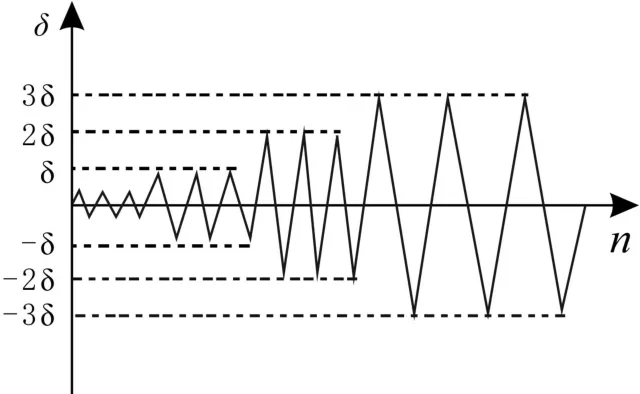
圖5 循環加載方案Fig.5 Cyclic loading program

圖6 施加邊界約束與荷載后的有限元模型Fig.6 Finite element models after constraining and loading

3 數值結果分析

3.1 有限元模型驗證

通過文獻[14]獲得試驗節點荷載—位移滯回曲線,轉化成彎矩—轉角滯回曲線(見圖7(b)的虛線).對ABAQUS有限元軟件建立的EERC-PN1節點有限元模型進行非線性分析,試件參數及加載方案與試驗相同,提取EERC-PN1試件的荷載—位移滯回曲線(見圖7(a)).通過轉化獲得彎矩—轉角滯回曲線[13](見圖7(b)的實線),由圖7可見,兩者吻合良好,表明有限元模型建立方法正確.

3.2 試件滯回曲線

利用ABAQUS有限元軟件開展8組試件的滯回分析,從Visualization模塊中提取試件的荷載—位移滯回曲線數據,利用excel軟件繪制荷載—位移滯回曲線(見圖8),不同試件提取包絡圖的結果見圖9.

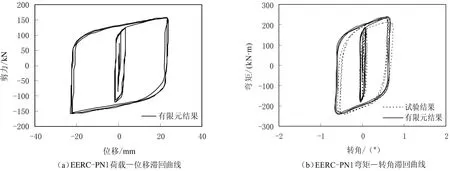
圖7 EERC-PN1試件有限元結果Fig.7 Finite element results of EERC-PN1

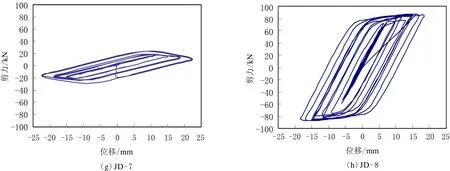
圖8 不同試件的荷載—位移滯回曲線Fig.8 Load-displacement hysteresis curves of different specimens

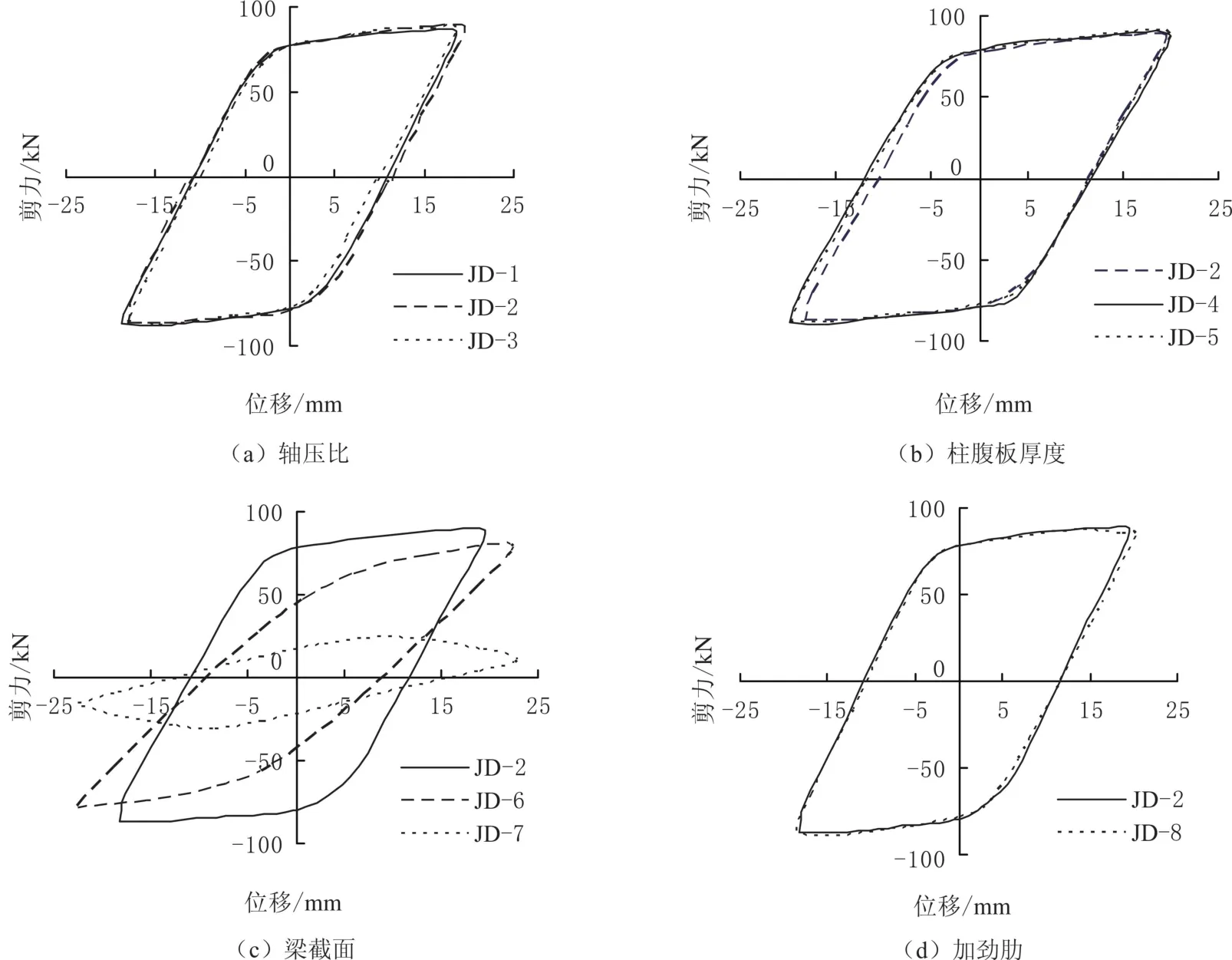
圖9 不同試件的包絡圖Fig.9 Envelope diagram of different specimens

由圖8可見,8組試件的荷載—位移滯回曲線比較飽滿,表現較好的塑性性能.由圖9(a)可見,試件JD-1、JD-2和JD-3包絡面積分別為3 501.4、3 681.5和3 376.2 k N·mm;由圖9(b)可見,試件JD-2、JD-4和JD-5包絡面積分別為3 681.5、3 956.5和3 898.3 k N·mm;由圖9(c)可見,試件JD-2、JD-6和JD-7包絡面積分別為3 681.5、2 324.1和1 161.3 k N·mm;由圖9(d)可見,試件JD-2和JD-8包絡面積分別為3 681.5和3 702.9 k N·mm.8組試件的滯回曲線呈紡錘形,滯回環飽滿,試件JD-1—JD-5、JD-8具有良好的耗能能力,試件JD-6和JD-7包絡面積較小,耗能能力相對較差.

由圖8和圖9可見:當軸壓比為0.2～0.4時,隨著軸壓比的增大,滯回環包絡面積增加,節點耗能能力增大;當軸壓比為0.4～0.6時,隨著軸壓比的增大,包絡圖面積減小,節點耗能能力降低.隨著柱腹板厚度的增加,滯回環越飽滿,節點耗能能力增大,延性增加;當腹板厚度過厚時,滯回環包絡面積略有減小,節點耗能能力稍有下降.當梁截面形式為H型鋼時滯回環最飽滿,包絡面積最大,節點耗能能力最強,延性最大,承載力最高;當梁截面形式為圓鋼管時,各項指標與H型鋼梁相比均有下降;當梁截面形式為方鋼管時,節點承載力最低,耗能能力和延性最差;設置加勁肋的節點滯回環更加飽滿,包絡面積增大,延性增加.

3.3 骨架曲線

試件滯回環最大值的連線形成骨架曲線,8組試件的骨架曲線見圖10.由圖10(a)可見,當軸壓比分別為0.2、0.4和0.6時,隨著軸壓比的增大,試件JD-1、JD-2和JD-3的節點承載力先增大后減小,節點初始剛度變化不明顯.由圖10(b)可見,當柱腹板與翼緣厚度比為0.625～0.750時,隨柱腹板厚度增加,試件JD-2、JD-4和JD-5的節點承載力及初始剛度變化不明顯;當柱腹板與翼緣厚度比為0.750～0.875時,節點承載力及初始剛度隨柱腹板厚度增加有減小趨勢.整體上,柱腹板厚度對十字型節點的影響不大,主要原因是“強柱弱梁”型節點的承載力及剛度主要是由鋼梁控制的.由圖10(c)可見,改變梁截面形式對節點的承載力及初始剛度影響較大,當梁截面形式為H型鋼時,試件JD-2、JD-6和JD-7的節點承載力和初始剛度最高;當梁截面形式為圓鋼管時,各項指標與H型鋼梁相比均有下降;當梁截面形式為方鋼管時,節點承載力及初始剛度最低.由圖10(d)可見,在節點處設置加勁肋,可有效提高試件JD-2和JD-8的節點初始剛度,節點屈服承載力明顯增大.

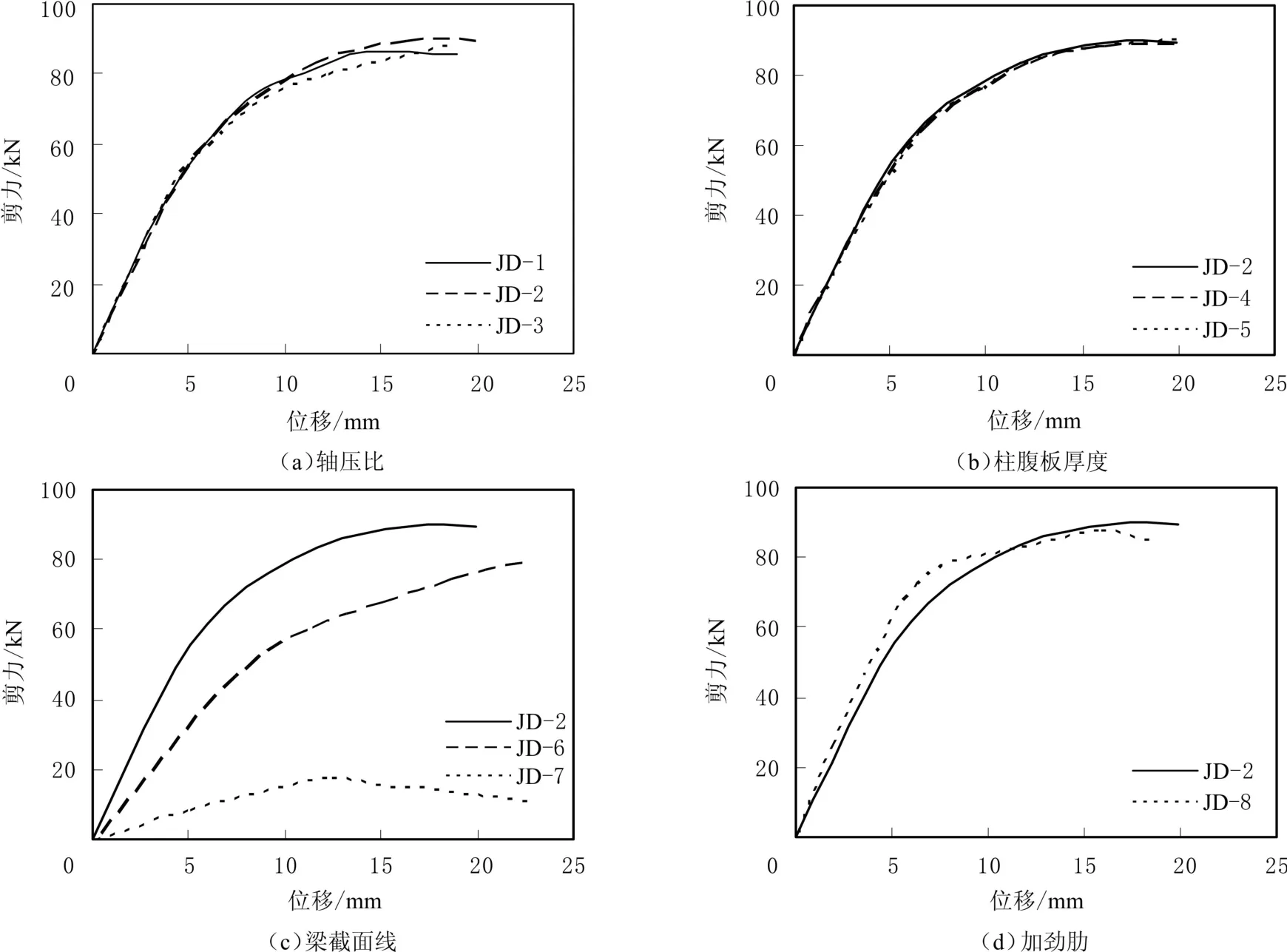
圖10 試件骨架曲線Fig.10 The skeleton curves of specimens

3.4 應力分析

利用ABAQUS有限元軟件的Visualization模塊,查看試件節點的應力云圖(見圖11).由圖11可見,試件節點最大應力均出現在梁上下翼緣與柱相接處,即彎矩最大處,材料已進入屈服階段,可見節點梁柱連接處最容易發生破壞.各試件梁翼緣與柱相接處最大應力見表4.由表4可見,隨著軸壓比的增大,梁翼緣與柱連接處最大應力先增大后減小;隨著柱腹板厚度增加,最大應力減小;試件JD-8節點梁柱連接處最大應力明顯降低,僅為285.33 MPa,可見設置橫向加勁肋可有效降低節點連接處的應力,耗能能力強,表現出較好的抗震性能;試件JD-6、JD-7節點處最大應力已達到鋼材的極限強度,節點發生破壞,說明圓鋼管或方鋼管構成的節點抗震性能是較差的.

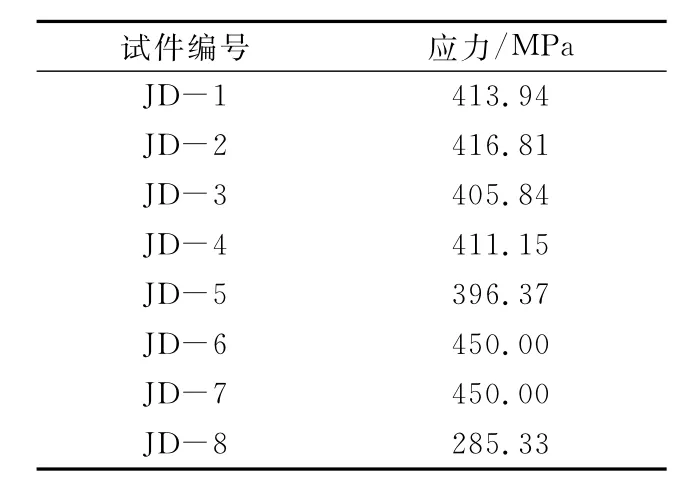
表4 梁翼緣與柱相接處應力Table 4 The stress for at the connection position of beam flange and column

4 設計建議

(1)分析時,在采用的軸壓比中軸力和材料強度是標準值,在工程中進行鋼結構設計時采用軸壓比設計值,兩者之間換算關系為

式中:N為軸向壓力;Nk為軸向壓力標準值;fy為鋼材抗拉強度設計值;fyk為鋼材抗拉強度標準值;A為型鋼截面面積.

圖11 不同試件的節點應力云圖Fig.11 Node stress nephogram for different specimens

對于梁柱截面為H型鋼的節點形式,節點柱的軸壓比小于0.4時,節點承載力、耗能能力隨著軸壓比的增大而增大;當軸壓比為0.4～0.6時,節點承載力、耗能能力隨著軸壓比的增大而減小,但延性降低不明顯,說明軸壓比為0.4是節點抗震承載力的限值.通過式(1)換算軸壓比為0.4對應的軸壓比設計值為0.53,因此為確保節點抗震承載力滿足要求,柱軸壓比設計限值建議取為0.5.

(2)鋼框架十字型剛性節點鋼梁截面形式為H型鋼時,節點在反復荷載作用下的滯回曲線相當飽滿,節點抗震性能良好,且遠遠優于圓鋼管及方鋼管的截面形式,因此在設計時梁柱宜采用H型截面形式.GB 50017-2012《鋼結構設計規范》在梁的受壓和受拉翼緣處,給出柱腹板厚度tw和柱翼緣板厚度tc相應規定,在地震作用下,鋼框架梁端將反復經歷拉壓過程,因此建議節點域柱腹板、翼緣板厚度保持不變,避免在節點域對柱進行焊接.

(3)柱腹板與翼緣厚度比不宜過大,當比值小于0.75時,節點承載力隨比值增大變化不明顯,但節點的耗能能力明顯增加;當比值大于0.75時,節點承載力、耗能能力隨著比值的增大而減小,因此柱腹板與翼緣厚度比限值取為0.75.

(4)設置橫向加勁肋的試件承載能力強,同等位移下與未設置橫向加勁肋的試件相比,節點材料應力偏小,說明通過在節點處設置橫向加勁肋能夠提高節點的抗震性能.橫向加勁肋能夠傳遞梁翼緣傳來的集中力,為增強抗剪能力,可在節點域布置斜向加勁肋,以傳遞節點域承擔剪力之外的剪力.節點域的抗剪強度應滿足:

式中:Mb1、Mb2分別為梁兩端彎矩;Vp為節點域剪力;fv為節點域抗剪強度.

5 結論

(1)利用ABAQUS有限元軟件,對鋼框架十字型剛性節點的抗震性能進行分析,以軸壓比、H型鋼柱腹板厚度、鋼梁截面形式及加勁肋為參數,設計8組鋼框架十字型剛性節點和1組T型剛性節點,給出簡化的力學模型和材料的本構關系,建立相應的有限元模型.

(2)基于T型節點分析,開展十字型節點仿真分析,獲得節點荷載—位移滯回曲線,提取包絡圖、骨架曲線和應力云圖并進行對比,分析軸壓比、H型鋼柱腹板厚度、梁截面形式及加勁肋對該類節點抗震性能的影響規律.

(3)對軸壓比、柱腹板與翼緣厚度比提出設計建議,柱軸壓比設計限值建議取為0.5,柱腹板與翼緣厚度比限值取為0.75.當截面形式為H型鋼時,該類節點的抗震性能良好,遠遠優于鋼管截面的,設置橫向加勁肋可有效提高節點的抗震性能.

[1] 張文福,趙文艷,李文,等.方鋼管混凝土偏心受壓構件承載力計算[J].大慶石油學院學報,2001,25(2):98-99.

Zhang Wenfu,Zhao Wenyan,Li Wen,et al.Calculation of on flexural stiffness of concrete-filled steel tube and its affecting factors[J].Journal of Daqing Petroleum Institute,2001,25(2):98-99.

[2] 張文福,郝進鋒,薛景宏,等.循環加載條件下鋼管混凝土應力—應變關系模型[J].大慶石油學院學報,2010,34(3):104-108.

Zhang Wenfu,Hao Jinfeng,Xue Jinghong,et al.Constitutive model of concrete filled circular steel tube brace members under cyclic load[J].Journal of Daqing Petroleum Institute,2010,34(3):104-108.

[3] 詹界東,張文福,王娜,等.預應力組合梁的彈性性能分析[J].大慶石油學院學報,2004,28(1):112-114.

Zhan Jiedong,Zhang Wenfu,Wang Na,et al.Elastic behavior analysis of prestressed composite beam[J].Journal of Daqing Petroleum Institute,2004,28(1):112-114.

[4] 張文福,郝進鋒,薛景宏,等.圓鋼管混凝土支撐滯回性能分析[J].大慶石油學院學報,2010,34(3):109-114.

Zhang Wenfu,Hao Jinfeng,Xue Jinghong,et al.Analysis of hysteretic performance of concrete filled circular steel tube brace members[J].Journal of Daqing Petroleum Institute,2010,34(3):109-114.

[5] 趙文艷.斜向受力方鋼管混凝土框架柱滯回性能分析[J].大慶石油學院學報,2003,27(2):114-116.

Zhao Wenyan.Analysis for hysteretic behavior of concrete-filled square steel tubular frame columns[J].Journal of Daqing Petroleum Institute,2003,27(2):114-116.

[6] 劉燕,郭成喜.梁腹板矩形洞口削弱型節點的滯回性能[J].鋼結構,2006,21(3):66-68.

Liu Yan,Guo Chengxi.Comparison between reduced beam section with rectangular openings on web and unreduced beam section connections[J].Steel Construction,2006,21(3):66-68.

[7] 戴紹斌,黃俊,朱健.翼緣削弱型剛性連接節點的受力性能研究[J].華中科技大學學報:自然科學版,2005,22(3):18-20.

Dai Shaobin,Huang Jun,Zhu Jian.Mechanical performance of flange weakening type rigid connection joint[J].Journal of Huazhong University of Science and Technology:Natural Science Edition,2005,22(3):18-20.

[8] 王秀麗,沈世釗,段占忠,等.鋼框架梁腹板開孔型連接節點力學性能試驗研究[J].工程力學,2006,23(6):65-76.

Wang Xiuli,Shen Shizhao,Duan Zhanzhong,et al.Experimental research on mechanical behavior of beam-column connections with openings on beam webs in steel frames[J].Engineering Mechanics,2006,23(6):65-76.

[9] 陳宏,石永久,王元清,等.鋼框架梁柱節點受力性能的非線性分析[J].工業建筑,2001,31(5):56-58.

Chen Hong,Shi Yongjiu,Wang Yuanqing,et al.Research on stressing properties of steel beam-column connections by nonlinear analysis[J].Industrial Construction,2001,31(5):56-58.

[10] 石永久,王萌,王元清,等.鋼框架梁柱組合節點滯回性能有限元分析[J].土木建筑與環境工程,2010,32(3):1-7.

Shi Yongjiu,Wang Meng,Wang Yuanqing,et al.FEM analysis on cyclic behavior of steel frame-composite connections[J].Journal of Civil,Architectural&Environmental Engineering,2010,32(3):1-7.

[11] 侯和濤,邱燦星,李國強.鋼框架結構與墻體(板)共同作用的研究[J].鋼結構,2010,25(4):25-28.

Hou Hetao,Qiu Canxing,Li Guoqiang.Research on the interaction between the steel frames and the infilled walls(panels)[J].Steel Construction,2010,25(4):25-28.

[12] 劉洪波,徐龍軍,張慶國,等.考慮樓板影響的鋼框架結構節點域數學模型[J].哈爾濱工業大學學報,2012,44(2):28-32.

Liu Hongbo,Xu longjun,Zhang Qingguo,et al.Models for panel zones in steel moment frame structures with composite action[J].Journal of Harbin Institute of Technology,2012,44(2):28-32.

[13] 石永久,王萌,王元清,等.鋼框架端板連接半剛性節點受力性能分析[J].工程力學,2011,28(9):21-58.

Shi Yongjiu,Wang Meng,Wang Yuanqing,et al.Analysis on the behavior of steel frame end-plate connections[J].Engineering Mechanics,2011,28(9):21-58.

[14] Jun Jin.Seismic performance of steel reduced beam section moment frame buildings[D].Orlando:Dissertation for Doctor Degree at the University of Central Florida,2002:95-107.

[15] 王玉鐲,傅傳國.ABAQUS結構工程分析及實例詳解[M].北京:中國建筑工業出版社,2010.

Wang Yuzhuo,Fu Chuanguo.ABAQUS analysis and detailed examples of structural engineering[M].Beijing:China Building Industry Press,2010.

[16] 石亦平,周玉蓉.ABAQUS有限元分析實例詳解[M].北京:機械工業出版社,2006.

Shi Yiping,Zhou Yurong.ABAQUS finite element analysis and detailed examples[M].Beijing:Machinery Industry Press,2006.

TU324.5

A

2095- 4107(2014)01- 0102- 10

2013- 10- 18;編輯:任志平

教育部高等學校博士學科點專項科研基金項目(新教師類:20122322120004);黑龍江省自然科學基金面上項目(E201336);國家自然科學基金項目(51178087)

計 靜(1977-),男,博士,教授,主要從事土木結構工程方面的研究.

DOI 10.3969/j.issn.2095-4107.2014.01.016