A Survey on the Sharp Blow-up Criteria for a Class of Nonlinear Schr?dinger Equations

ZHANG Jian, ZHU Shihui

(College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan)

1 Introduction

In this paper,we consider the following Cauchy problem of nonlinear Schr?dinger equations

In fact,equation(1)is proposed by Davey and Stewartson in 1974 and is also called Davey-Stewartson system(see[1]).In fluid mechanics,Davey-Stewartson system models the evolution of weakly nonlinear water wave having one predominant direction of travel,and the wave amplitude is modulated slowly in two horizontal directions.

When the singular integral operatorEis replaced by the harmonic potential,i.e.E=-|x|2,equation(1)is called the nonlinear Schr?dinger equation with a harmonic potential.This equation models the remarkable Bose-Einstein condensate with attractive inter-particle interactions under a magnetic trap(see[2-4]).Physicists and mathematicians are very interested in studying dynamics of this equation(see[2,4-5]).Oh[6]established the local well-posedness in the corresponding energy fieldΣ={u∈H1(RN)||x|u∈L2(RN)}.Cazenave[5],Zhang[3,7],Shu and Zhang[8],Chen and Zhang[9],Carles[10]studied the existence of blow-up solutions and sharp thresholds of blow-up and global existence.Carles[10]also gave the transformation which reveals the relationship between the nonlinear Schr?dinger equation with and without a harmonic potential.Recently,Merle and Rapha?l[11-13]obtained a large body of breakthrough work for the super-critical mass blow-up solutions with the help of the Spectral Properties[12],such as sharp blow-up rates,profiles of blow-up solutions,etc.Then,using this transformation proposed by Carles[10],Zhang,Li and Wu[14-16]obtained some dynamical properties of blowup solutions such as sharp blow-up rates,L2-concentration and rate ofL2-concentration etc.Zhu,Zhang and Li[17]obtained the limiting profile of blow-up solutions in the natural energy fieldΣ={u∈H1(RN)||x|u∈L2(RN)}.

For the Cauchy problem(1)～(2),Ghidaglia and Saut[18],Guo and Wang[19]established the local well-posedness in the energy spaceH1(RN)forN=2 andN=3 respectively(see[5,20]for a review).Cipolatti[21],Zhang and Zhu[22]studied the existence of the standing waves.Cipolatti[23],Ohta[24-25],Gan and Zhang[26]investigated the stability and instability of standing waves.Ghidaglia and Saut[18],Guo and Wang[19]studied the existence of blow-up solutions,and Wang and Guo[27]further discussed the scattering of global solutions.Ozawa[28]constructed some exact blow-up solutions.Richards[29], Papanicolaou et al[30],Gan and Zhang[26,31], Shu and Zhang[32],Zhang and Zhu[22]studied the sharp conditions of blow-up and global existence for the Cauchy problem(1)～(2).Li et al[33],Richards[29]obtained the mass-concentration properties of the blow-up solutions inL2-critical case whenN=2.

In the present paper,we are focusing on the sharp criteria of blow-up and global existence for the Cauchy problem(1)～(2).First,whenN=2,3,by constructing a type of cross-constrained variational problem and establishing so-called cross-constraint manifolds of the evolution flow,a sharp threshold for blow-up and global existence of the solutions to the Cauchy problemis given.Secondly,forN=2,by using the profile decomposition of bounded sequences inH1,a precisely sharp criterion of the blow-up solutions for the Cauchy problem(1)～(2)with 3≤p＜+∞ is given.Thirdly,forN=3,by using the profile decomposition of bounded sequences inH1,a precisely sharp threshold of the blow-up solutions for the Cauchy problem(1)～(2)withis given.We should point out that most of the above results has been published.There are two main aims of this survey.One is to give a collection about the sharp criteria of blow-up and global existence for equation(1),and it is convenient for readers to refer.The other is to give main sketch to obtain the above sharp criteria,and it may be quite useful for students to handle this method.

2 Preliminaries

The functionalH(u(t))is well-defined according to the Sobolev embedding theorem and the properties of the singular operatorE.Ghidaglia and Saut[18],Guo and Wang[19]established the local well-posedness of the Cauchy problem(1)～(2)in energy spaceH1.

Proposition 2.1LetN∈{2,3}andu0∈H1.There exists a unique solutionu(t,x)of the Cauchy problem(1)～(2)on the maximal time[0,T)such thatu(t,x)∈C([0,T)；H1)and eitherT=+∞(global existence),orT＜+∞and=+∞ (blow-up).Furthermore,for allt∈[0,T),u(t,x)satisfies the following conservation laws.

(i)Conservation of mass‖u(t)‖2=‖u0‖2.

(ii)Conservation of energyH(u(t))=H(u0).

By some basic calculations,we have the following proposition(see Ohta[25]).

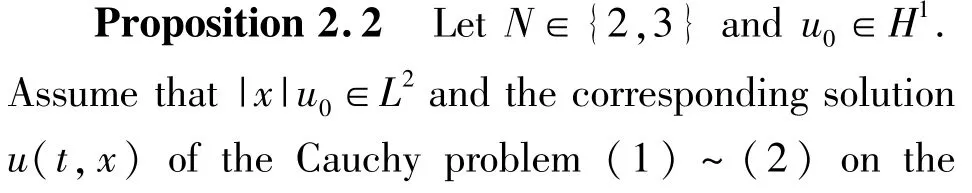
3 Cross-constrained Variational Methods and Sharp Criteria

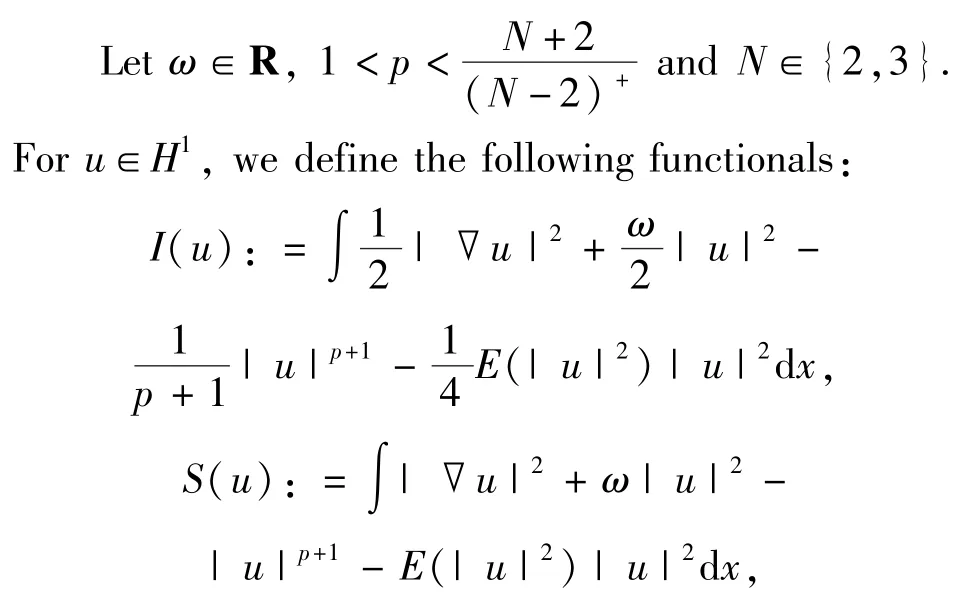
4 Profile Decomposition and Sharp Criteria for N=2

5 Profile Decomposition and Sharp Criteria for N=3

First,using the profile decomposition of bounded sequence inH1,we compute the best constant of a generalized Gagliardo-Nirenberg inequality in dimension three.More precisely,we have the following theorems.

(i)If‖?u0‖2＜y0,then the solutionu(t,x)of the Cauchy problem(1)～(2)exists globally.Moreover,for all timet,u(t,x)satisfies

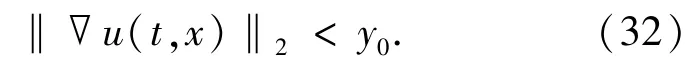
(ii)If‖?u0‖2＞y0and|x|u0∈L2,then the solutionu(t,x)of the Cauchy problem(1)～(2)blows up in finite timeT＜+∞,wherey0is the unique positive solution of the equationg(y)=0 andg(y)is defined in(27).

[1]Davey A,Stewartson K.On three-dimensional packets of surfaces waves[J].Proc Royal Soc,1974,A338:101-110.

[2]Wadati M,Tsurumi T.Critical number of atoms for the magnetically trapped Bose-Einstein condensate with negative s-wave scattering length[J].Phys Lett,1998,A247:287-293.

[3]Zhang J.Stability of attractive Bose-Einstein condensate[J].J Stat Phys,2000,10(1):731-746.

[4]Bradley C C,Sackett C A,Hulet R G.Bose-Einstein condensation of lithium:Observation of limited condensate number[J].Phys Rev Lett,1997,78:985-989.

[5]Cazenave T.Semilinear Schr?dinger equations[C]//Courant Lecture Notes in Mathematics,10.NYU:CIMS,AMS,2003.

[6]Oh Y G.Cauchy problem and Ehrenfest's law of nonlinear Schr?dinger equations with potentials[J].J Diff Eqns,1989,81:255-274.

[7]Zhang J.Sharp threshold for blowup and global existence in nonlinear Schr?dinger equations under a harmonic potential[J].Commun PDE,2005,30:1429-1443.

[8]Shu J,Zhang J.Nonlinear Schr?dinger equation with harmonic potential[J].J Math Phys,2006,47:063503-1-6.

[9]Chen G G,Zhang J.Sharp threshold of global existence for nonlinear Gross-Pitaevskii equation in RN[J].IMA J Appl Math,2006,71:232-240.

[10]Carles R.Critical nonlinear Schr?dinger equations with and without harmonic potential[J].Math Models Methods Appl Sci,2002,12:1513-1523.

[11]Merle F,Rapha?l P.On universality of blow-up profile forL2critical nonlinear Schr?dinger equation[J].Invent Math,2004,156:565-672.

[12]Merle F,Rapha?l P.Blow-up dynamic and upper bound on the blow-up rate for critical nonlinear Schr?dinger equation[J].Ann Math,2005,16:157-222.

[13]Merle F,Rapha?l P.On a sharp lower bound on the blow-up rate for theL2-critical nonlinear Schr?dinger equation[J].J Amer Math Soc,2006,19:37-90.

[14]Li X G,Zhang J.Limit behavior of blow-up solutions for critical nonlinear Schr?dinger equation with harmonic potential[J].Diff Integral Eqns,2006,19:761-771.

[15]Li X G,Zhang J,Wu Y H.Mathematical analysis of the collapse in Bose-Einstein Condensate[J].Acta Math Sci,2009,B29:56-64.

[16]Zhang J,Li X G,Wu Y H.Remarks on the blow-up rate for critical nonlinear Schr?dinger equation with harmonic potential[J].Appl Math Comput,2009,208:389-396.

[17]Zhu S H,Zhang J,Li X G.Limiting profile of blow-up solutions for the Gross-Pitaevskii equation[J].Sci China:Math,2009,A52:1017-1030.

[18]Ghidaglia J M,Saut J C.On the initial value problem for the Davey-Stewartson systems[J].Nonlinearity,1990,3:475-506.

[19]Guo B L,Wang B X.The Cauchy problem for Davey-Stewartson systems[J].Commun Pure Appl Math,1999,52:1477-1490.

[20]Sulem C,Sulem P L.The nonlinear Schr?dinger equation:Self-focusing and wave collapse[C]//Appl Math Sci,139.New York:Springer-Verlag,1999.

[21]Cipolatti R.On the existence of standing waves for a Davey-Stewartson system[J].Commun PDE,1992,17:967-988.

[22]Zhang J,Zhu S H.Sharp blow-up criteria for the Davey-Stewartson system in R3[J].Dynamics PDE,2011,8:239-260.

[23]Cipolatti R.On the instability of ground states for a Davey-Stewartson system[J].Ann Inst Henri Poincaré:Phys Theor,1993,58:85-104.

[24]Ohta M.Stability of standing waves for the generalized Davey-Stewartson system[J].J Dynam Diff Eqns,1994,6:325-334.

[25]Ohta M.Instability of standing waves the generalized Davey-Stewartson systems[J].Ann Inst Henri Poincare:Phys Theor,1995,63:69-80.

[26]Gan Z H,Zhang J.Sharp threshold of global existence and instability of standing wave for a Davey-Stewartson system[J].Commun Math Phys,2008,283:93-125.

[27]Wang B X,Guo B L.On the initial value problem and scattering of solutions for the generalized Davey-Stewartson systems[J].Sci China:Math,2001,A44:994-1002.

[28]Ozawa T.Exact blow-up solutions to the Cauchy problem for the Davey-Stewartson systems[J].Proc Roy Soc London,1992,A436:345-349.

[29]Richards G.Mass concentration for the Davey-Stewartson system[J].Diff Integral Eqns,2011,24:261-280.

[30]Papanicolaou G C,Sulem C,Sulem P L,et al.The focusing singularity of the Davey-Stewartson equations for gravity-capillary surface waves[J].Physica,1994,D72:61-86.

[31]Gan Z H,Zhang J.Sharp conditions of global existence for the generalized Davey-Stewartson system in three dimensional space[J].Acta Math Scientia,2006,A26:87-92.

[32]Shu J,Zhang J.Sharp conditions of global existence for the generalized Davey-Stewartson system[J].IMA J Appl Math,2007,72:36-42.

[33]Li X G,Zhang J,Lai S Y,et al.The sharp threshold and limiting profile of blow-up solutions for a Davey-Stewartson system[J].J Diff Eqns,2011,250:2197-2226.

[34]Gérard P.Description du defaut de compacite de l'injection de Sobolev[J].ESAIM Control Optim Calc Var,1998,3:213-233.

[35]Hmidi T,Keraani S.Blowup theory for the critical nonlinear Schr?dinger equations revisited[J].Internat Math Res Notices,2005,46:2815-2828.

[36]Weinstein M I.Nonlinear Schr?dinger equations and sharp interpolation estimates[J].Commun Math Phys,1983,87:567-576.

[37]Zhang J.Cross-constrained variational problem and nonlinear Schr?dinger equation[C]//Cucker F,Rojas J M.Proc Smalefest 2000.Found Comput Math.New Jersey:World Scientific,2002.

[38]Zhang J.Sharp conditions of global existence for nonlinear Schr?dinger and Klein-Gordon equations[J].Nonlinear Anal,2002,48:191-207.

[39]Holmer J,Roudenko S.On blow-up solutions to the 3D cubic nonlinear Schr?dinger equation[J].Appl Math Research Express,2007,2007:4.

[40]Kwong M K.Uniqueness of positive solutions of Δu-u+up=0 in Rn[J].Arch Rational Mech Anal,1989,105:243-266.

[41]Strauss W A.Existence of solitary waves in higher dimensions[J].Commun Math Phys,1977,55:149-162.