Q0-SM環及其w-全局變換環

周德川, 王芳貴

（四川師范大學數學與軟件科學學院,四川成都610066）

乘法理想理論為整環的刻畫提供了許多方法,人們希望這樣的做法能用于一般的交換環上.傳統上,通過用交換環的完全分式環T（R）來替換整環的商域,也獲得了一些對應的結果（參見文獻［1-3］）.但這樣的做法最終未能普及,其原因是關于整環的許多經典結果在一般交換環上未能有一個對應描述.例如,當R是整環時,R是整閉整環當且僅當多項式環R［X］是整閉整環.盡管可以借助T（R）定義一般交換環的整閉包和在T（R）中的整閉整環,但1979年J.W.Brewer等［4］指出,R是在T（R）中約化的整閉環,未必有R［X］在T（R［X］）中整閉.因此,用T（R）替代整環的商域未必是最好的方法.T.G.Lucas［5］嘗試用Q0（R）來替代整環的商域,用于研究一般交換環上可能展開的乘法理想理論；1989年他證明了R是在Q0（R）中整閉的約化環當且僅當R［X］在Q0（R［X］）中是整閉的.于是2004年,T.G.Lucas［6］借助Q0（R）與半正則理想把Mori整環推廣到一般交換環上,定義了Q0-Mori環,并對其進行了很多的討論.在此基礎上,本文定義了Q0-SM環,即交換環R滿足半正則w-理想的升鏈條件,且若｛In｝是R的半正則v-理想的降鏈,∩In是半正則理想,則｛In｝穩定,并對其基本性質進行了討論.已知SM整環是Mori整環、Mori整環是TV整環、TV整環是H整環,本文相應地定義了Q0-H環、Q0-TV環,并證明了此關系依然存在.證明了若R是Q0-TV環,則R的半正則t-理想只包含在有限多個極大w-理想中.若R是Q0-SM環,則R的半正則理想只包含在有限多個半正則極大w-理想中.然后定義了一般交換環R的w-全局變換環Rw*,并證明了R是Q0-SM環,則Rw*也是Q0-SM環且

t-dim（Rw*）＝t-dim（R）-1.

1 Q0-SM環

設R是交換環,J是R的有限生成理想,如果自然同態φ:M→J*＝HomR（J,R）是同構,則J稱為R的GV-理想,用GV（R）表示R的GV-理想全體.I是R的理想,若I中包含R的一個正則元,則I稱為R的正則理想；若存在I的有限生成子理想I0,使得ann（I0）＝0,則I稱為R的半正則理想.用S0表示R的所有有限生成半正則理想的集合,T（R）表示R的完全分式環,Q0（R）＝｛u∈T（R［X］）｜存在I∈S0,使得Iu?R｝.設

α＝∑aiXi/∑biXi∈T（R［X］）,

則α∈Q0（R）當且僅當對任何i、j有aibj＝ajbi.R-模B?Q0（R）是R的分式理想是指存在R的半正則理想I,使得IB?R.若B包含一個Q0（R）的非零因子,且存在R的正則元r,使得rB?R,則B稱為R的正則分式理想；若B包含一個沒有非零零化子的有限生成分式理想,且存在R的有限生成半正則理想I,使得IB?R,則B稱為R的半正則分式理想.R-模M是w-模是指:M是GV-無撓模,且對任何J∈GV（R）,定義模M的包絡,Mw＝｛x∈E（M）｜存在J∈GV（R）,使得Jx?M｝,M是w-模當且僅當Mw＝M.若A是Q0（R）中的R-子模,記

A-1＝（R∶A）＝｛t∈Q0（R）｜tA?R｝.

I是R的分式理想,當（I（R∶I））w＝R時,則I稱為w-可逆分式理想.當I是半正則分式理想時,（R∶I）也是半正則分式理想；當I是正則分式理想時,（R∶I）也是正則分式理想.且對任何半正則分式理想I,有（R∶I）＝（R∶I）v,由（R∶I）w?（R∶I）v知,有（R∶I）＝（R∶I）w.并且有It＝∪｛（I0）v｜其中I0取遍I的所有有限生成半正則子分式理想｝［6］.

下面來看半正則理想及其包絡的一些性質.

定理1.1設I是R的有限生成半正則理想,則I是GV-理想當且僅當I-1＝R.

定理1.2設I是R的半正則理想,則Iw＝R當且僅當It＝R.

證明設It＝R.則有I的有限生成子理想B,使得1∈Bv.于是有B-1＝R.不妨設B就是半正則理想,由定理1.1知,B∈GV（R）.從而有R＝Bw?Iw?R,即有Iw＝R.反之顯然成立.

引理1.31）設I,J是環R的半正則分式理想,則（IJ）w＝（IJw）w＝（IwJw）w；

2）設I是R的真w-理想,則存在R的極大w-理想m,使得I?m.因此,R一定有極大w-理想,且極大w-理想都是素理想；

3）設m是R的半正則素理想,則m是極大w-理想當且僅當m是極大t-理想.

證明1）、2）驗證是常規的.

4）設m是極大t-理想,若m不是極大w-理想,則存在R的極大w-理想p,使得m?p.于是pt＝R,由于p是半正則的,由定理1.2,pw＝R,矛盾.

反之,設m是極大w-理想.若m不是極大t-理想,則mt＝R,有mw＝R,矛盾.

為了得到Q0-SM環的定義,需先回顧一下R的有限型模的相關概念.

定義1.4設f:M→N是R-模同態,若對R的任何極大w-理想m,fm:Mm→Nm是單同態（滿同態或同構）,則f稱為w-單同態（w-滿同態或w-同構）.

定理1.5設M是R-模,若存在有限生成自由模F及w-滿同態g:F→M,則M稱為有限型的R-模.

命題1.6設M是R-模.

1）M是有限型的當且僅當存在M的有限生成子模B,使得對R的任何極大w-理想m,Mm＝Bm.

2）若M是GV-無撓模,則M是有限型的當且僅當存在M的有限生成子模B,使得Mw＝Bw,從而M是有限型的當且僅當Mw是有限型的.

相應可以給出t-有限型,v-有限型的概念.Q0（R）是GV-無撓模,故R的分式理想都是GV-無撓模.若R的一個分式理想A是t-有限型的,當且僅當存在A的有限生成子分式理想I,使得At＝It；若R的一個分式理想A是v-有限型的,當且僅當存在A的有限生成子分式理想I,使得Av＝Iv.

定理1.7設P是R的半正則非有限型的w-理想集合的極大元,則P是R的素w-理想.

證明顯然有P是w-理想且P≠R.對r,x∈R,rx∈P,若r,x?P,來推出矛盾.令B＝｛z∈R｜rz∈P｝.于是（P+rR）w與B是半正則w-理想且都真包含P,從而是有限型的.不妨設

這與假設矛盾,因此有P是素w-理想.

已知整環R是SM整環是指整環R滿足w-理想的升鏈條件,環R是SM環是指環R滿足正則w-理想的升鏈條件,相應地來定義弱Q0-SM環.

定義1.8環R稱為弱Q0-SM環是指R滿足半正則w-理想的升鏈條件.

定理1.9對環R,以下等價:

1）R是弱Q0-SM環；

2）R的每一半正則w-理想是有限型的；

3）R的每一半正則w-理想的非空集合有極大元；

4）R的每一半正則素w-理想是有限型的；

5）R的每一半正則理想是有限型的.

證明1）?2） 設I是R的半正則w-理想,則存在I的有限生成子理想I0,使得ann（I0）＝0,故I0是I的有限生成半正則子理想.若I不是有限型的,可取0≠x1∈I-I0,及n＞1時,

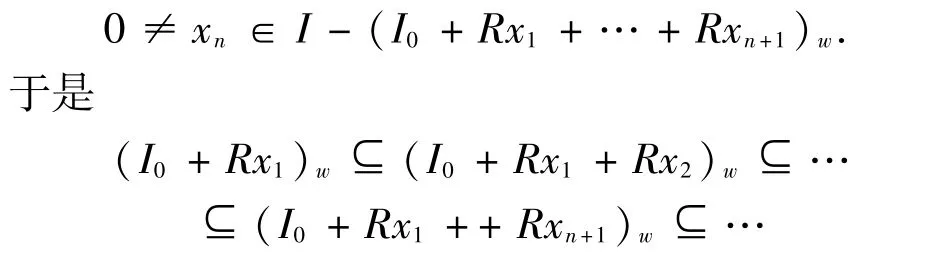
是R的半正則w-理想升鏈,但不是穩定的,矛盾.故I是有限型的.

2）?3） 設Γ是R的半正則w-理想的非空集合.設｛Ii｝是Γ中的一個全序子集.令I＝∪iIi,容易驗證I是R的半正則w-理想.由已知I是有限型的,由命題1.6知,存在I的有限生成子理想I0＝（a1,a2,…,an）,使得Iw＝（I0）w.由于Ii是全序子集,存在Ik∈｛Ii｝,使得I0?Ik,故I?Iw＝（I0）w?（Ik）w＝Ik?Iw＝I,因此有I＝Ik.于是I是該全序子集的上界.由Zorn引理知,Γ中有極大元.

3）?1） 設I1?I2?…?In?…是R的半正則w-理想升鏈.由條件,Γ＝｛In｝中有極大元素In.于是當m≥n時,Im＝In.因此,該鏈是穩定的,故R是弱Q0-SM環.

2）?4） 顯然.

4）?2） 若不然,則有R的半正則非有限型的w-理想的集合S是非空集.由Zorn引理知,S中有極大元,設為p,由定理1.7知,p是素w-理想,從而p是有限型的,矛盾.

2）?5） 由命題1.6的2）即知.

定理1.10設環R,以下等價:

1）R是弱Q0-SM環；

2）對每個有限生成半正則理想Im的升鏈,存在正整數n,k≥n時,有（Ik）w＝（In）w.

證明1）?2） ｛Im｝是有限生成半正則理想升鏈,則｛（Im）w｝是半正則w-理想的升鏈,由于R是弱Q0-SM環,故此升鏈穩定,即存在正整數n,k≥n時,有（Ik）w＝（In）w.

2）?1） 由定理1.9知,只需證R的半正則理想是有限型的.反證法,假設存在R的半正則理想I不是有限型的.設J1是I的有限生成半正則理想,則（J1）wIw,因此存在a2∈I-J1,使得J2＝J1+a2R是R的有限生成半正則理想,且（J1）w（J2）wIw.又存在a3∈I-J2,使得J3＝J2+a3R是R的有限生成半正則理想,且

依次類推,有一個升鏈｛（Jm）w｝,由2）知,存在正整數n,k≥n時,有（Jk）w＝（Jn）w,與假設矛盾.故1）成立.

定義1.11環R稱為Q0-SM環是指R是弱Q0-SM環且若｛In｝是R的半正則v-理想的降鏈,∩In是半正則理想,則｛In｝有降鏈條件.

定義1.12環R稱為Q0-Mori環是指R滿足半正則v-理想的升鏈條件且若｛In｝是R的半正則v-理想的降鏈,∩In是半正則理想,則｛In｝有降鏈條件.

定理1.13Q0-SM環是Q0-Mori環.

證明由半正則v-理想是半正則w-理想即知.

定理1.14若R是Q0-SM環,則R的半正則分式理想是v-有限型的.

證明由定理1.13及文獻［6］定理2.5及定理2.7即知.

2 Q0-H環及Q0-TV環

已知SM整環是Mori整環,Mori整環是TV整環,TV整環是H整環,本文相應地定義了Q0-H環,Q0-TV環,并證明了此關系依然存在,并且對于Q0-SM環的討論,很多時候都會用到Q0-H環,Q0-TV環的相關性質,故本文就Q0-H環,Q0-TV環進行了定義,并對他們進行了淺顯的討論.證明了若R是Q0-TV環,則R的半正則t-理想只包含在有限多個半正則極大w-理想中.若R是Q0-SM環,則R的半正則理想只包含在有限多個半正則極大w-理想中.

定義2.1對環R的任何半正則理想I,只要I-1＝R,就有一個J∈GV（R）,使得J?I,則R稱為Q0-H環.

定理2.2設R是交換環,以下各條等價:

1）R是Q0-H環；

2）R的每個半正則極大w-理想是v-理想；

3）設I是R的半正則理想,若I-1＝R,則Iw＝R.

證明1）?2） 設R是Q0-H環,m是R的半正則極大w-理想,若mv＝R,則m-1＝R,于是有J∈GV（R）,使得J?m,這與m是w-理想矛盾,因此mv≠R,由m的極大性有mv＝m.

2）?3） 設I是R的半正則理想,若I-1＝R,則Iv＝R.若Iw≠R,由引理1.3知存在R的極大w-理想m,使得I?m,由條件Iv?mv＝m,矛盾.因此有Iw＝R.

3）?1） 顯然.

定義2.3若環R的半正則t-分式理想都是v-分式理想,則R稱為Q0-TV環.

定理2.4Q0-TV環是Q0-H環.

證明設R是Q0-TV環,m是R的半正則極大w-理想,由引理1.3知m也是R的極大t-理想,因此m是v-理想,由定理2.2知,R是Q0-H環.

引理2.5設I是R的半正則v-理想,｛Bi｝是R的一簇包含I的v-理想,則

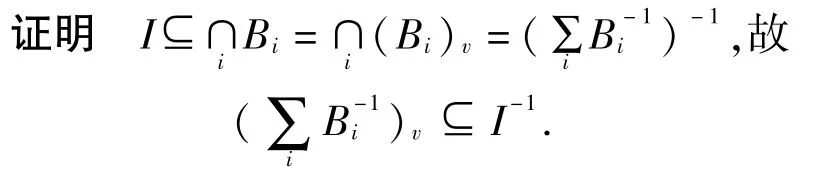
定理2.6設R是Q0-TV環,I是R的半正則t-理想,m是包含I的極大w-理想,設｛Bi｝是R的包含I,但不包含于m的半正則t-理想的集合,則∩iBim.

證明對任何B∈｛Bi｝,Bm,由定理2.4知,m是極大v-理想.故（m+B）v＝R,這推出m-1∩B-1＝R.選擇x∈m-1-R,對任何B∈｛Bi｝,x?B-1.由引理2.5,,故可取I的有限生成半正則理想I0,使得

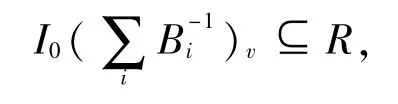
定理2.7設R是Q0-TV環,I是R的半正則t-理想,則I只包含在有限多個極大w-理想中.

證明設｛mi｝表示R的包含I的極大w-理想的集合.注意,每一mi是半正則理想.對任意i,令由定理2.6知,所有包含I但不包含于mi的t-理想的交不包含于mi,從而Timi,因此對任何i,Tmi.由于I?T,故對任何半正則極大w-理想m,Tm,于是有Tt＝R,從而1∈Tt.故存在有限多個T1,T2,…,Tn,使得

設對應的極大w-理想為m1,m2,…,mn,則m1,m2,…,mn就是包含I的全部極大w-理想.事實上,若還有極大w-理想mj,使得I?mj,則Ti?mj,i＝1,2,…,n,因此?mj,矛盾.

定理2.8Q0-Mori環是Q0-TV環.

證明若R是Q0-Mori環,I是R的半正則t-分式理想,由參考文獻［6］定理2.5及2.7知,存在I的有限生成半正則分式理想J,使得Iv＝Jv有

I＝It?Iv＝Jv＝Jt?It＝I,

故I＝Iv,所以I是v-分式理想,故Q0-Mori環是Q0-TV環.

定理2.9設R是Q0-TV環,則R的半正則極大w-理想是半正則極大v-理想.

證明由引理1.3知.

定理2.10設R是Q0-Mori環,則R的半正則極大w-理想是極大v-理想,且對R的任何半正則理想I,只有有限多個半正則極大w-理想包含I.

證明由定理2.8及定理2.9即知R的半正則極大w-理想是極大v-理想.

注意到包含I的半正則極大w-理想必然包含It,故包含I,It的半正則極大w-理想是一樣的.由定理2.7知,It只包含在有限多個極大w-理想中,故I只包含在有限多個半正則極大w-理想中.

推論2.11R是Q0-SM環,則R的半正則極大w-理想是極大v-理想,且R的半正則理想只包含在有限多個半正則極大w-理想中.

證明 由定理1.13及定理2.10知.

3 Q0-SM環的w-全局變換環

設p是R的半正則素t-理想,稱

pn?pn-1?pn-2?…?p1＝p0＝p

為R中長度為n的半正則素t-理想鏈,其中每個pi是R的半正則素t-理想,這樣的n的上確界稱為半正則素t-理想p的t-高度,記為t-htp＝n.且定義t-dim（R）＝sup｛t-htp｜p取遍R的所有半正則素t-理想｝.與整環的全局變換環相對應,來定義交換環的w-全局變換環Rw*.Rw*＝｛x∈Q0（R）｜存在R的半正則極大w-理想p1,p2,…,pn,使得p1p2…pnx?R｝.下面用w*-Max（R）來表示R的所有半正則極大w-理想的集合.對任何GV-無撓的Rw*-模B,用BW表示其作為Rw*-模的w-包絡,以便與其作為R-模的w-包絡相區別.

定義3.1設R?T是環擴張,其中T作為R-模是GV-無撓模.如果T作為R-模是w-模,即Tw＝T,則T叫做R上的w-linked擴張.當T?Q0（R）時,也稱T是R的w-linked擴環.

引理3.2Rw*是R的w-linked擴環.

致謝四川師范大學研究生優秀論文培育基金（校研字20131434）對本文給予了資助,謹致謝意.

［1］ Yin H Y,Wang F G,Zhu X S,et al.w-Modules over commutative rings［J］.J Korean Math Soc,2011,48（1）:207-222.

［2］ Rotman J J.An Introduction to Homological Algebra［M］.New York:Academic Press,1979.

［3］ Xie L,Wang F G,Yang T.On w-linked overrings［J］.J Math Research ＆ Exposition,2011,31（2）:337-346.

［4］Brewer J W,Costa D L,McCrimmon K.Seminormality and root closure in polynomial rings and algebraic curves［J］.J Algebra,1979,58:217-226.

［5］ Lucas T G.Characterizing when R［X］ is integrally closed［J］.Proc Am Math Soc,1989,105:861-867.

［6］ Lucas T G.The Mori property in rings with zero divisors［J］.Lecture Notes Pure Appl Math,2004,236:379-400.

［7］王芳貴.交換環與星型算子理論［M］.北京:科學出版社,2006.

［8］王芳貴.有限表現型模與w-凝聚環［J］.四川師范大學學報:自然科學版,2010,33（1）:1-9.

［9］趙松泉,王芳貴,陳翰林.交換環上的w-模是平坦模［J］.四川師范大學學報:自然科學版,2010,35（3）:364-366.

［10］ Huckaba J A.Commutative Rings with Zero Divisors［M］.New York:Marcel Dekker Inc,1979.

［11］ Dessagnes N.Intersections d'anneaux de Mori-exemples［J］.Port Math,1987,44:379-392.

［12］ Wang F G,McCasland R L.On strong Mori domains［J］.Pure Appl Algebra,1999,135:155-165.

［13］熊濤,王芳貴,胡葵.余純投射模與CPH環［J］.四川師范大學學報:自然科學版,2013,36（2）:198-201.

［14］ Badawi A,Lucas T G.On phi-Mori rings［J］.Houston J Math,2006,32:1-32.

［15］ Chang G W.Strong Mori domains and the ring D［X］Nv［J］.J Pure Appl Algebra,2005,197:293-304.

［16］ Doering S,Lequain Y.Chains of prime ideals in polynomial rings［J］.J Algebra,1982,78:163-180.