基于無裂紋直耳片接頭接觸問題的非線性分析
徐 丹,李朝光,王學強,朱親強
(中航工業洪都,江西南昌330024)
0 引言
耳片型接頭是飛機結構中常用的連接型主要構件,其使用環境較惡劣,極易造成疲勞損傷,引起失效,是飛機結構中最具斷裂危險的原件之一。關于耳片損傷容限設計,需要在新結構的危險部位存在小的初始缺陷時,進行預計結構的疲勞裂紋擴展壽命和剩余強度。而在含有初始裂紋連接耳片的分析中,普偏關心的基本項目是無裂紋狀態下的應力分布[1]。
無裂紋耳片結構形式雖然簡單,但耳孔周圍的應力狀態卻較復雜。耳片連接件主要通過螺栓給耳片傳遞載荷,隨著載荷的增加,耳孔與螺栓的接觸由線接觸變化到半個螺栓面的接觸。螺栓和耳孔內表面傳力過程屬于接觸應力問題,是典型非線性問題,采用常規的彈性力學的解析方法很難確定邊界形狀及接觸狀態,因此對于耳孔周圍的應力狀態也很難分析。
目前已有一些文獻[2],給出了一些特定參數下規則的直耳片的應力強度因子。本文從有限元分析的方法出發,采用彈簧元來模擬螺栓和耳片的接觸形式,調節彈簧元的接觸剛度,分析計算了耳片的孔邊應力。給出了規律性的結果,為含初始裂紋連接耳片分析提供了探討性研究,為耳片損傷容限設計做鋪墊。
1 有限元模型及方法
接觸問題屬于典型非線性問題,接觸問題所特有的接觸截面非線性有兩個方面的原因[3]:其一,接觸區域截面大小和位置以及接觸狀態不僅事先都是未知的,而且隨著時間的變化,需要在求解過程中確定;其二,接觸條件的非線性,即接觸物體的不可相互侵入、接觸力的法向分量只能是壓力、切向接觸的摩擦條件。
接觸問題的關鍵與難點在于接觸界面條件的定義。彈性接觸理論方法都是通過一些簡單的數學公式來解決接觸問題,對于一些接觸形狀復雜的問題很難用解析公式表示。有限元法將接觸截面劃分為一系列的單元,單元之間以節點連接。這些單元結構形狀簡單,易于用平衡關系或能量關系建立節點之間的邊界條件,為求解工程中的復雜接觸問題提供了有利手段。
1.1 有限元模型
為了使結構具有代表性,模型選擇了飛機耳片接頭中典型對稱的直耳片進行分析。螺栓和耳片均采用六面體單元,分別取不同的R0/Ri值,螺栓載荷作用在0°方向。本文給定耳片與螺栓的初始間隙均為0.01mm。
1.2 接觸邊界處理
采用彈簧元來處理螺栓和耳片接觸點間的位移協調問題,假設螺栓和耳片之間是光滑凈配合,不考慮摩擦力。
借助于賦予彈簧元在壓縮時很高的剛度和在拉伸時很低的剛度,通過迭代,使接觸點對之間滿足法向接觸協調條件。
假設任一可能接觸點對為i、j[4],見圖1,法向位移分別為δni、δnj,接觸間隙為ΔXij,初始間隙為ΔX0ij,法向節點彈簧力為Pi,則接觸判定條件表示為:
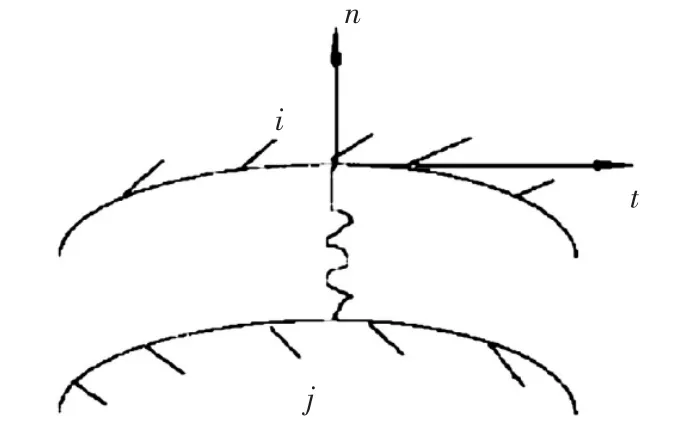
圖1 接觸點對示意圖

通過接觸的判定條件,判別耳片與螺栓的接觸面。由于模型選擇在0°方向加載,接觸面積為耳片與螺栓接觸的半圓周上。因此有限元模型中定義了半個圓周上的彈簧元。
1.3 耳片外載荷分配
耳片通過與螺栓的相互擠壓來傳遞載荷,應力分析時,假設載荷和應力沿耳片厚度方向保持不變,載荷按余弦規律分布[2]在螺栓和耳片相互作用的擠壓面上,見圖2。

圖2 沿耳孔擠壓面上的載荷示意圖
擠壓面上i的徑向載荷為:

徑向沿x,y方向的載荷為:
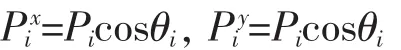
因此,沿0°加載的總合力為:
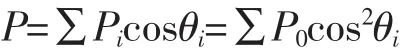
式中:Pi為外載荷P作用線通過擠壓面上A單元分配的載荷;θi為耳孔擠壓面上i點偏離外載荷方向的角度。
因此可根據外載荷來獲得沿耳孔擠壓面上每個彈簧元分配的載荷,進而調節彈簧元的剛度來協調位移。
1.4 彈簧元剛度的定義
假設螺栓移動微小位移ΔX,即整個耳片向載荷加載的方向平移ΔX,見圖3。那么在螺栓和耳片相互作用的擠壓面i點的徑向位移為:

則,在螺栓與耳片相互作用的擠壓面i上的彈簧元剛度應為:

2 有限元計算結果及分析
2.1 應力集中系數的理論算法
根據文獻[2]提供直耳片孔邊應力集中系數的計算的經驗公式為:
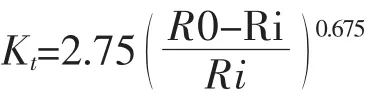
注:Kt為孔邊最大切向應力按平均擠壓應力正則化所得。
依據上式,現給出不同R0/Ri情況下的孔邊應力集中系數,見表1。
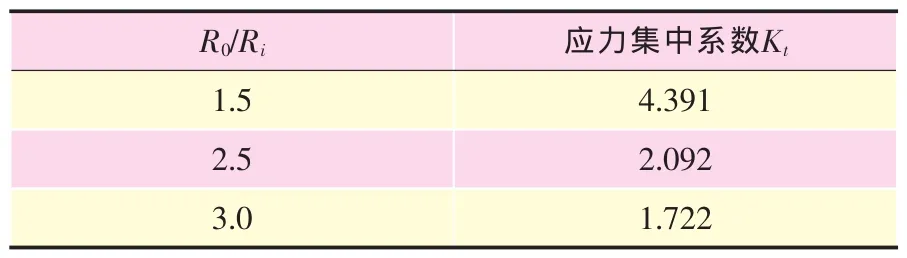
表1 不同耳片對應的應力集中系數
2.2 有限元計算結果與理論結果比較
選取三種不同半徑的接頭耳片進行計算分析,三種計算模型的幾何尺寸如表2所示。
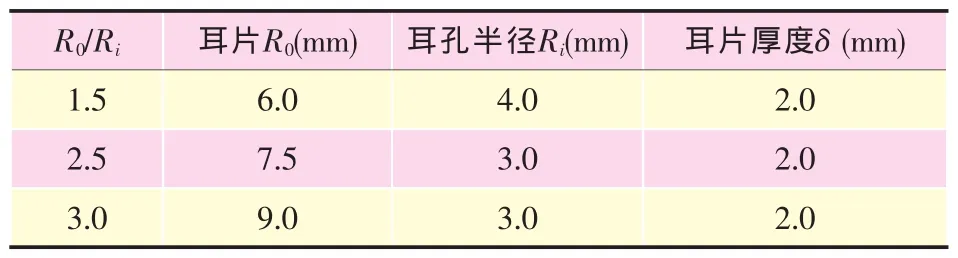
表2 兩種情況計算模型幾何參數
計算結果見圖3、圖4、圖5,圖中所示為最大剪切應力云圖。
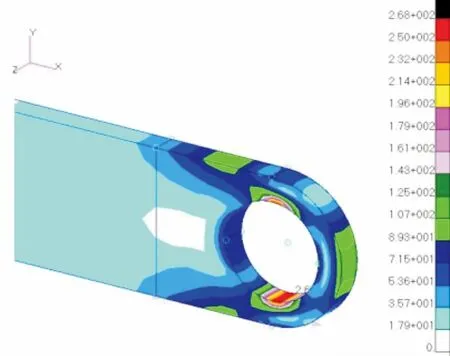
圖3 R0/Ri=1.5有限元應力云圖
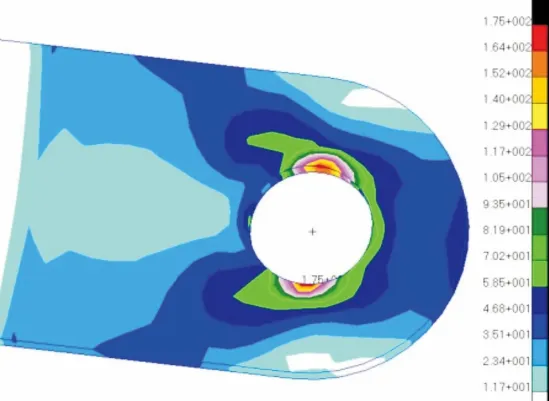
圖4 R0/Ri=2.5有限元應力云圖

圖5 R0/Ri=3有限元應力云圖
比較有限元計算結果與理論計算結果對應的孔邊應力集中系數,見表3。
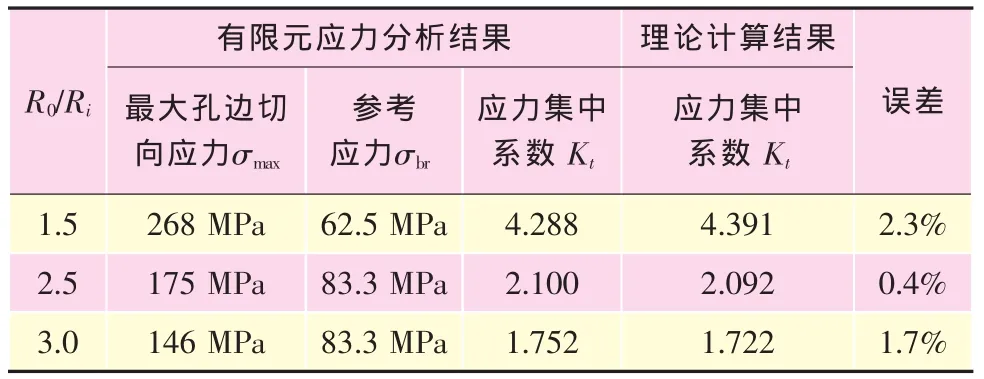
表3 有限元應力分析結果與理論計算結果比較
從表3中數據可以看出:有限元應力分析結果與理論計算的結果相近,說明運用彈簧元能夠較真實地模擬耳片與螺栓之間的接觸問題。
2.3 幾何尺寸對應力集中系數的影響
1)相同 R0/Ri情況比較
相同R0/Ri情況下兩種耳片的幾何參數與對應的計算結果見表4。
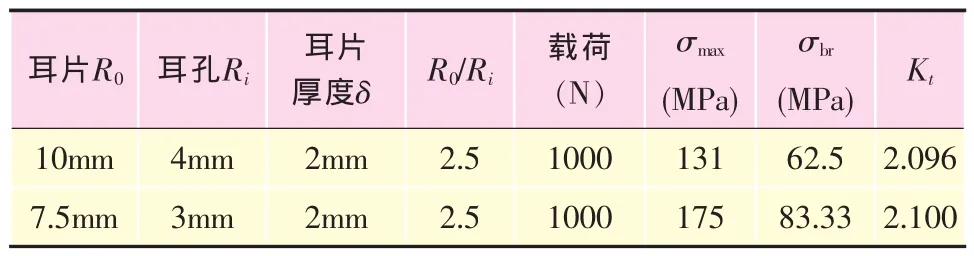
表4 兩種耳片幾何參數及加載結果比較
根據表4比較結果可以看出,具有相同值的不同耳片,其孔邊最大剪切應力集中系數一致。
2)厚度對應力集中系數的影響
根據表5比較結果可以看出,不同厚度耳片,其孔邊最大剪切應力集中系數趨于一致,說明耳片的厚度對耳片的應力集中系數不影響。
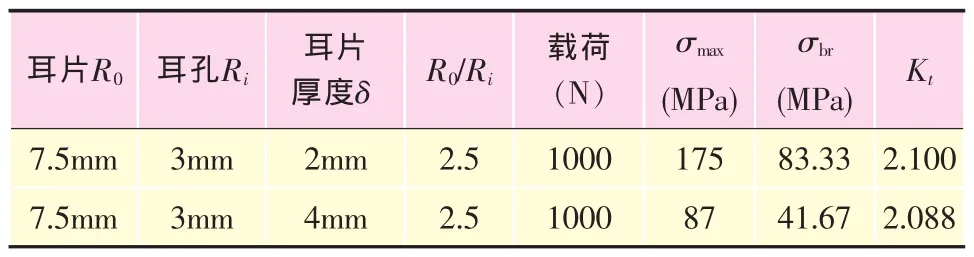
表5 兩種耳片幾何參數及加載結果比較
3 結語
1)本文采用彈簧元處理螺栓和耳片接觸點間的位移協調問題。通過外載荷獲得沿耳孔擠壓面上每個彈簧元分配的載荷,調節彈簧元的剛度來協調位移。
2)通過有限元方法建立了三種不同大小的耳片,計算得到危險點的應力集中系數與理論計算結果較一致的應力集中系數和耳片應力分布情況,能夠較真實地模擬無裂紋直耳片與螺栓之間的接觸問題。
3)具有相同值的不同耳片,有相同的應力集中系數和應力分布情況;耳片厚度不影響耳片的應力集中系數,與理論經驗公式相符合。
[1]吳富民.結構疲勞強度[M].西安:西北工業大學出版社,1985.
[2]樊東黎.熱處理工程師手冊.北京:機械工業出版社,2004,9.
[3]飛機結構強度研究所.航空結構連接件疲勞分析手冊.南京:飛機結構強度研究所,1985.
[4]黃其青.對稱與非對稱斜削耳片危險部位及應力強度因子的有限元分析.航空學報,1998,19(4).

