艦空導彈對空火力分配研究

周榮坤，張永利，計文平

（中國電子科技集團公司電子科學研究院，北京100041）

0 引 言

對空目標威脅估計是艦艇編隊防空作戰過程進行火力分配的重要理論依據。現代海戰中，空襲的主要模式是多層次、多批次、多類型的飽和攻擊，所以威脅估計需要針對不同類型的來襲目標，并把來襲目標各評估要素關聯起來。本文建立了適于防空系統的威脅評估模型，得到目標的威脅度并實現評估結果排序，同時根據評估結果，結合艦空導彈毀傷概率對目標實行火力分配。

1 威脅估計

防空作戰中，及時準確地判斷來襲目標的威脅程度，是合理進行防空火力分配的重要前提。關于目標威脅評估的研究有很多［1－6］。通常情況下，根據來襲目標的屬性，建立威脅評估模型可以分為4個層次：

（1）確定威脅評估要素；

（2）建立各評估要素的數學表達式；

（3）綜合各因素求取目標威脅度；

（4）確定來襲目標威脅等級。

1.1 空中目標威脅評估影響因素

選擇來襲目標威脅評估因素不僅要反映目標的威脅程度，而且要便于量化。威脅評估影響因素既包含定性因子，也包含定量因子。

本文將來襲目標類型、高度、距離、速度作為威脅評估的主要影響因素，其中目標類型為定性指標，具有模糊集特征，由專家根據作戰經驗等實際情況用語言變量描述給出；高度、距離、速度為定量指標，由傳感器測得參數并進行數據處理得到。

1.2 目標威脅評估模型

1.2.1 定性指標的Vague值表示方法

目標類型對于目標威脅度的影響，很難通過具體公式進行處理。本文通過Vague值11級語言變量表示，將指標變量轉換成Vague值，取值在［0，1］之間，如表1所示。

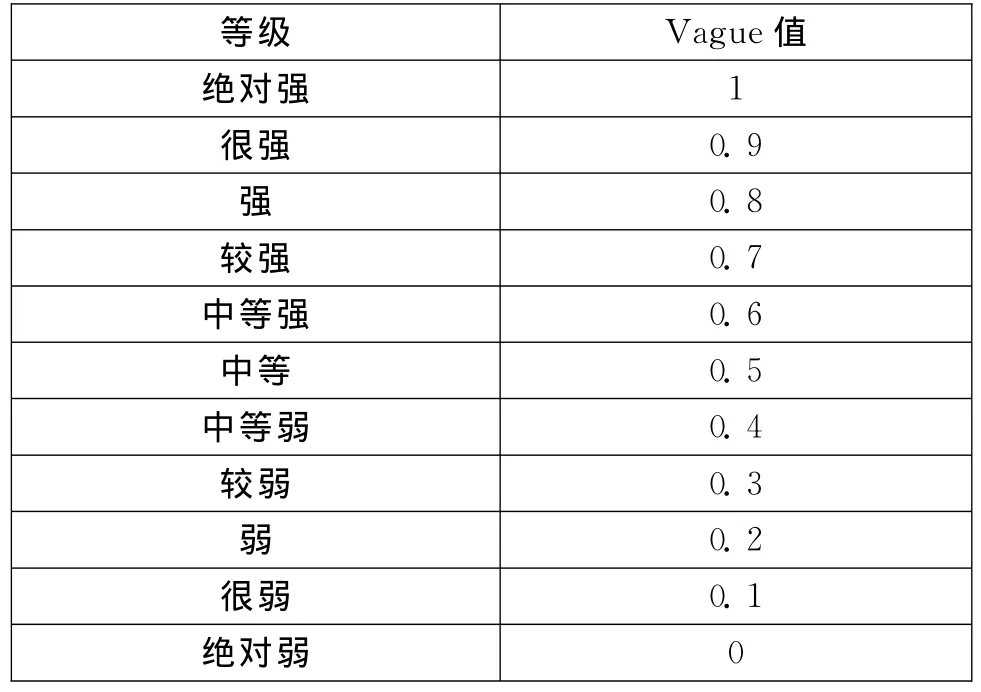
表1 Vague值表示的11級語言變量

1.2.2 定量指標的數學表達式

1.2.2.1 目標與艦艇編隊的距離

目標距離是指來襲目標到達艦艇編隊的距離。按距離因素計算目標威脅度的數學表達式為：

式中：r1，r2為目標威脅的最近距離和最遠距離。

當目標與艦艇編隊的距離逼近到一定范圍內，即r≤r1時，來襲目標對艦艇編隊造成毀滅性的打擊，即其威脅計算結果為最大值1；當來襲目標與艦艇編隊遠離到一定程度，即r≥r2時，對艦艇編隊基本不造成威脅，可認為其威脅計算結果為最小值0。

1.2.2.2 目標距艦艇編隊的高度

來襲目標的高度是指目標所在位置到水平航路的距離。威脅目標離艦艇編隊的高度越低，攻擊意圖越明顯，對艦艇編隊的威脅也越大；目標高度越高，威脅程度越小。按高度因素計算目標威脅度的數學表達式為：

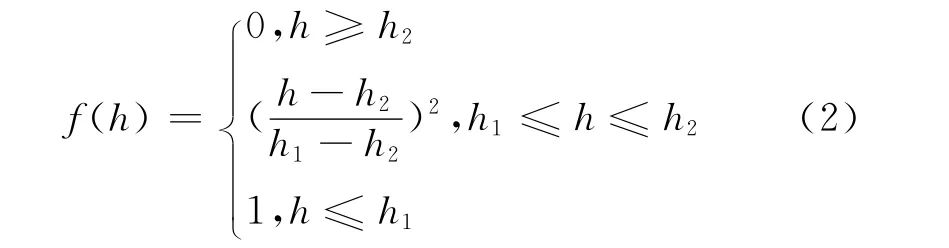
式中：h1，h2分別為目標威脅的最低高度和最高高度。

1.2.2.3 目標的速度

當目標速度達到其最大值的時候，認為該目標對艦艇編隊的威脅達到最大值1，當目標以最小速度飛行時，認為其對艦艇編隊的威脅為較弱的值，可定義為0.3。目標威脅度與目標速度的數學表達式為：

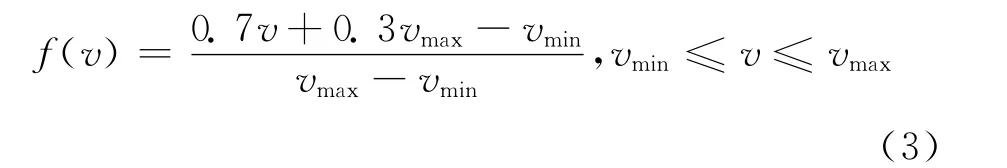
式中：vmax，vmin為目標飛行速度的最大值和最小值。

1.3 艦艇編隊目標威脅估計

1.3.1 數據源描述數據源描述如表2所示。

表2 數據源描述

根據Vague值表示以及公式（1）～（3），得到目 標定性和定量指標威脅屬性值μij，如表3所示。

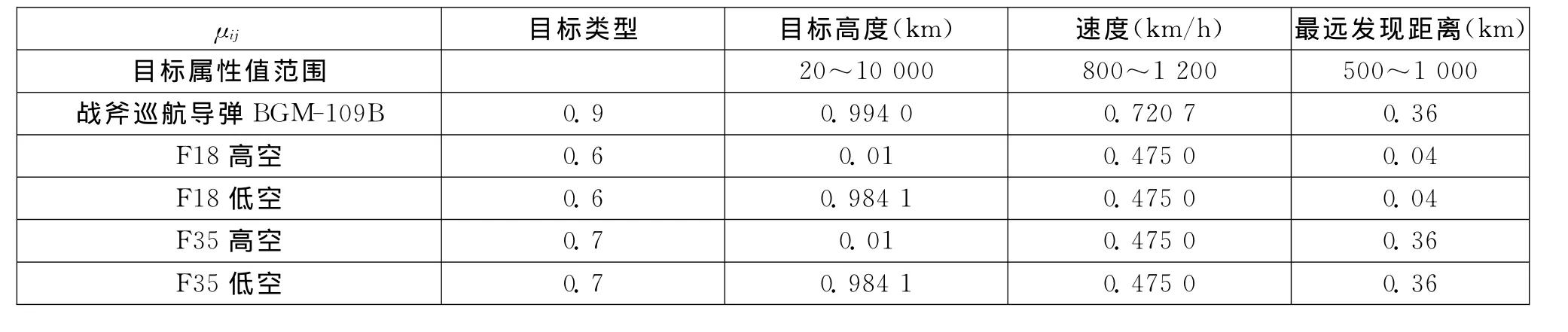
表3 目標影響因素的威脅屬性值

1.3.2 各威脅評估因素的權重設置

對來襲目標進行威脅評估，不同的評估影響因子具有不同的權重系數。文中利用層次分析法確定威脅目標影響因子的權重值。

計算判斷矩陣每行所有元素的幾何平均值：

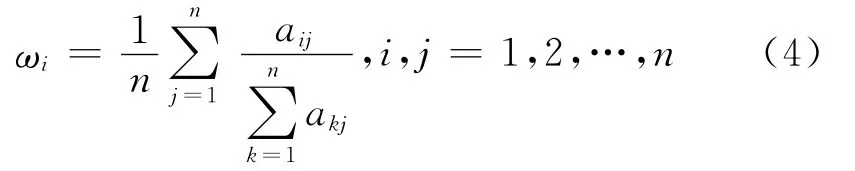
于是得到W ＝ （ω1，ω2，…，ωi）T。

計算判斷矩陣的最大特征根：

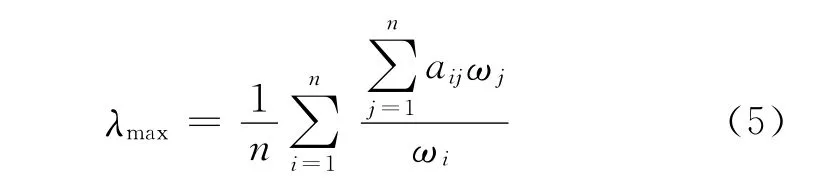
為了避免由于估計誤差引起特征值和特征向量產生偏差，導致判斷不一致，需要求出一個判斷矩陣一致性的指標IC，即：

隨著n的增加，判斷誤差就會增加，因此應當考慮到n的影響，使用隨機性一致性比值：

式中：IR為平均隨機一致性指標，如表4所示。

當RC＜0.1時，判斷矩陣的一致性是可以接受的。

表4 平均隨機一致性指標

采用層次分析法確定來襲目標影響因子的權重向量為：W＝（0.387 3，0.139 7，0.274 8，0.198 1）T，其中λmax＝4.121 7，IC＝0.040 6，IR＝0.89，RC＝0.045 6＜0.1，判斷矩陣的一致性是可以接受的。

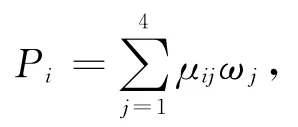
表5 GAMILLER量化理論

將各目標的威脅度轉換為5個威脅等級，如表6所示。

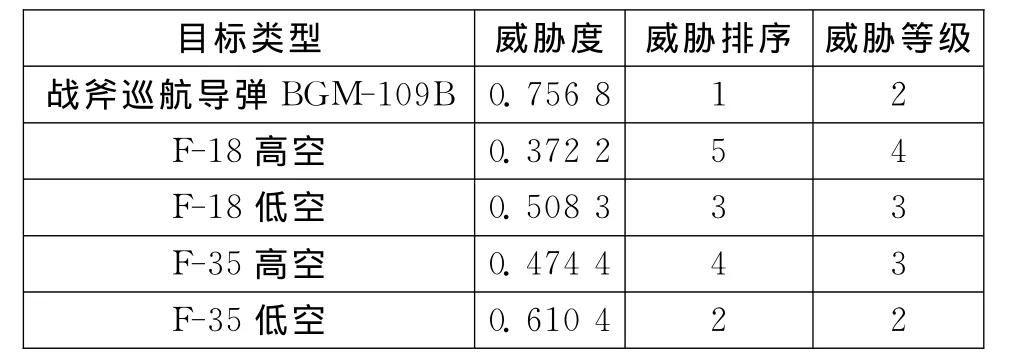
表6 各目標相當于艦艇編隊威脅計算結果

通過表6可知，敵巡航導彈的威脅程度最大，威脅等級最高，應首先對其實施射擊。其他依次為F－35低空、F－18低空、F－35高空和F－18高空。

2 火力分配的數學模型

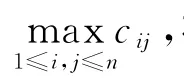
假設一個編隊具有m組不同類型的武器系統（也可以理解為m個導彈武器發控中心），編隊通過其偵察預警系統發現有n個敵來襲目標。第i組武器系統由mi（i＝1，2，…，m）個單位組成。空中來襲目標的威脅度系數為ωj，易損性系數為eij。其中eij（i＝1，2，…，m；j＝1，2，…，n）為第i組武器系統對第j個目標的單位毀傷概率。導彈武器的火力分配可用矩陣X＝（xij）m×n來描述，其中xij是用于第j個目標的第i組導彈武器的數量。

最優分配的目標函數是使對目標的毀傷效能指標達到最大。通常一定數量的第i類武器毀傷第j個目標的概率可表示為：

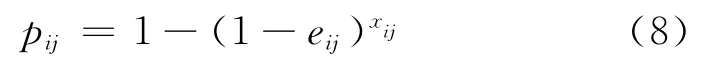
因而，所有m類武器對目標j的毀傷概率：

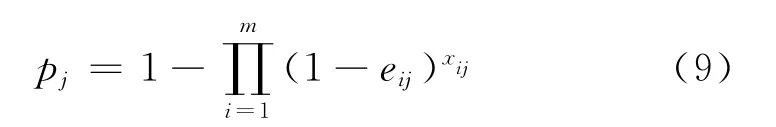
毀傷目標數的數學期望值M為：

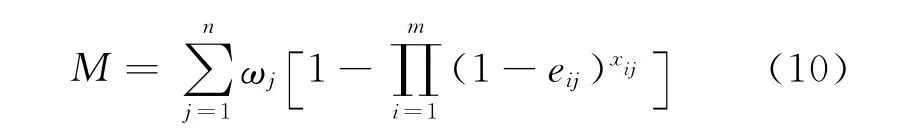
所以，最優化火力分配模型為：

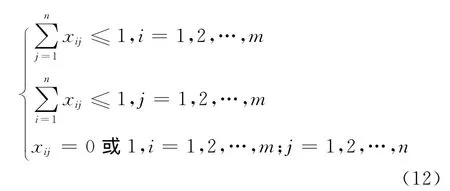
將上述非線性的整數規劃問題轉化為能夠用匈牙利算法求解的線性整數規劃問題：

式中：cij＝ωjeij。

3 艦空導彈火力分配

假設我艦艇編隊某型導彈驅逐艦具有2種不同類型的艦空導彈，攻擊敵威脅目標，第1種導彈具有3個單位，第2種導彈的數量為2個單位。目標的威脅度和每種導彈毀傷各個目標的概率如表7所示，要求攻擊每個目標的導彈數不超過2個，研究艦空導彈分配方案，使得目標毀傷效能指標達到最大。

根據上節可得各威脅目標的威脅度，結合2型艦空導彈對各威脅目標的毀傷概率（見表7），設xij為第i（i＝1，2）種導彈分配給第j（j＝1，2，…，5）個目標的數量，則目標函數為：

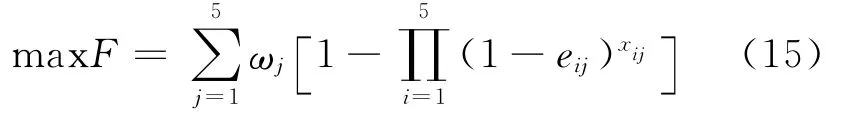
表7 目標的重要程度和導彈毀傷概率

同時，還應滿足下列約束條件：

目標威脅度ωj＝（0.756 8，0.372 2，0.508 3，0.474 4，0.610 4）

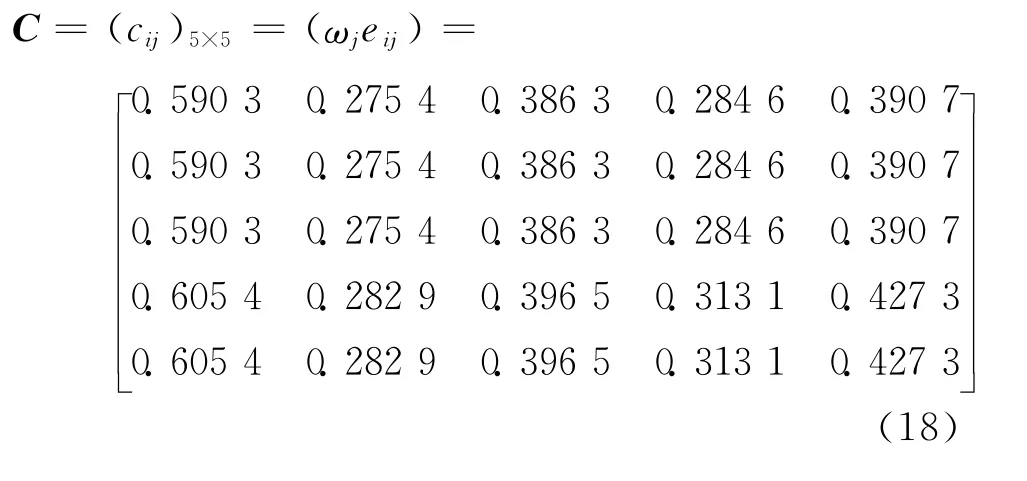
矩陣R運用匈牙利算法［10－12］得到最優解矩陣：

艦艇編隊艦空導彈最優火力分配方案見表8。

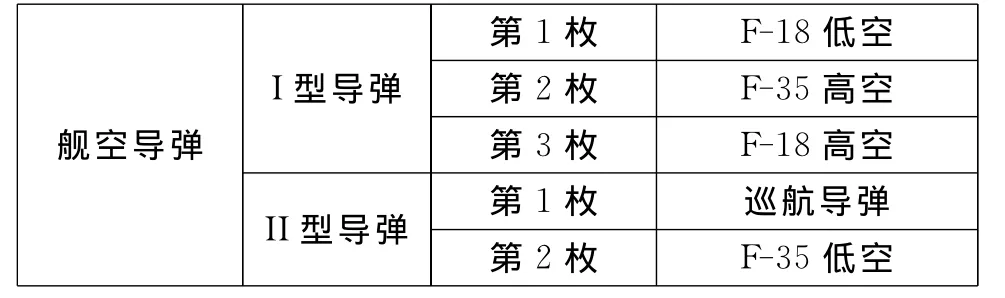
表8 艦空導彈火力分配方案

4 結束語

空中多目標對艦艇編隊攻擊的威脅評估和排序是目標分配和火力分配的基礎。本文針對艦艇編隊的空中多目標威脅因素進行分析，對來襲目標威脅程度進行了評估，并根據目標的威脅度和艦空導彈對各目標的毀傷概率，得到艦空導彈對威脅目標的最優火力分配方案。

［1］蘇曼，康鳳舉，謝攀.艦艇多目標威脅評估及可視化方法綜合 研 究 ［J］.科 學 技 術 與 工 程，2010，10（8）：1893－1897.

［2］曹睿婷，章衛國，李廣文.基于多層次分析方法的目標威脅估計研究［J］.彈箭與制導學報，2011，31（2）：30－32.

［3］郭輝，徐浩軍，周莉.基于區間數TOPSIS法的空襲目標威脅評估［J］.空軍工程大學學報，2011，12（1）：40－45.

［4］王小藝，劉載文，侯朝楨.基于模糊多屬性決策的目標威脅估計方法［J］.控制與決策，2007，22（8）：859－32.

［5］耿濤，盧廣山，張安.基于Vague集的空中目標威脅評估群決策方法［J］.系統工程與電子技術，2011，33（12）：2686－2690.

［6］尹高揚，周紹磊，張文廣.艦艇對來襲反艦導彈威脅評估算法［J］.兵工自動化，2011，30（12）：1－4.

［7］張年春，沈培華.編隊導彈攻擊的火力分配研究［J］.戰術導彈技術，2007（3）：36－39.

［8］依鳴.中國艦艇編隊編隊中的驅逐艦［J］.兵工科技，2013（S0）：27－35.

［9］張洋.多目標防空火力分配技術研究［D］.大連：大連大學，2012.

［10］黃力偉，許品剛，王勤.基于匈牙利算法求解的火力分配問題［J］.火力與指揮控制，2007，32（6）：25－28.

［11］柳毅，佟明安.匈牙利算法在多目標分配中的應用［J］.火力與指揮控制，2002，27（4）：34－37.

［12］王勇，吳梅，侯俊，潘泉.基于匈牙利算法的協同作戰排序問題最優解［J］.彈箭與制導學報，2005，25（3）：209－211.