Runge-Kutta法在微分方程初值問題中的應用

郭志萍

（浙江工業大學化材學院，浙江 杭州 310014；山西水利職業技術學院，山西 運城 044004）

Runge-Kutta法在微分方程初值問題中的應用

郭志萍

（浙江工業大學化材學院，浙江 杭州 310014；山西水利職業技術學院，山西 運城 044004）

本文利用Taylor級數推導了二階Runge-Kutta算法，并得到了經典的四階Runge-Kutta法。結合Matlab語言，在微分方程的初值問題中應用Runge-Kutta法數值計算了一階微分方程和高階微分方程組。Runge-Kutta法能夠較高精度地數值模擬數學建模所建立的微分方程。

Runge-Kutta法；Matlab；微分方程；數值計算

一、引言

微分方程是自然科學和社會科學研究中非常重要且十分實用的一種數學工具。Runge-Kutta法是一類具有相當實用價值的方法，也是最常用的一種數值方法。在數值求解微分方程初值問題中應用廣泛,張鵬利對兩空泡的共振頻率,共振振幅及空化噪聲聲壓利用Runge-Kutta法進行了數值求解；Runge-Kutta法在振蕩電路求解中的應用；淹沒磨料射流的運動分析，等等。應用Runge-Kutta法來數值求解，能夠較高精度地數值模擬數學建模所建立的微分方程，其計算與實驗結果吻合較好。這種方法能夠解決的問題越來越多，越來越復雜，在微分方程數值求解方法中扮演著非常重要的角色。

Matlab的基本單位是矩陣，它的表達式與數學、工程計算中常用的形式十分相似，極大地方便了人們學習和使用。利用Matlab提供各種數學工具，可以避免做繁瑣的數學推導和計算，方便地解決了很多數學問題。

本文從理論上對Runge-Kutta法進行了推導，運用Matlab語言，在具體的微分方程初值問題算例中詳細地給以求解。

二、初值問題數值解

除常系數線性微分方程可用特征根求解，少數特殊方程可用初等積分法求解外，大部分微分方程無顯式解，應用中主要靠數值解。考慮一階常微分方程組初值問題：

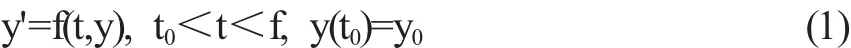
其中 y=(y1,y2,L,ym)T，f=(f1,f2,L,fm)T，y0=(y10,y20,L,ym0)T，這里表示轉置。所謂數值解，就是尋求y(t)在一系列離散節點t0＜t1＜L＜tn〈tf上的近似值 yk(k=0,1,L,n)。稱 hk=tk+1-tk為步長，通常取為常量h。

高階的常微分方程初值問題可以化為一階常微分方程組，已給一個n階方程：y(n)=f(t,y,y',L,y(n-1))T

設y1-y,y2=y',y1-y,L,yn=y(n-1),式(9)化為一階方程組：

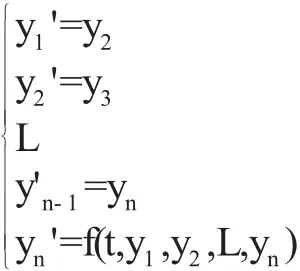
三、Runge-kutta法推理過程

Runge-kutta方法是一種單步法，是用函數f在tk和tk-1之間值的有限差分近似代替高階導數。下面以二階為例來推導：Taylor級數

中多保留一項，可得到二階Taylor級數法

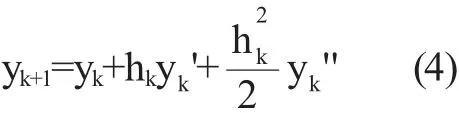
通過鏈式法對求導，即

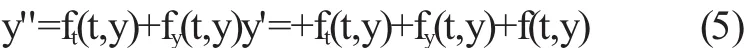
其中的下標表示的是給定變量求偏導。

由此得到

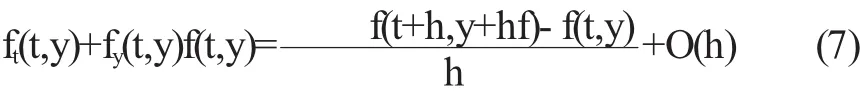
用上式近似二階導數，得到Runge-Kutta法

其中 k1=f(tk,yk)，k2=f(tk+hk,yk+hkk1)

Runge-kutta方法優點：計算tk+1時刻的值時，并不需要tk時刻以前的值。

最著名的是四階經典的Runge-kutta格式

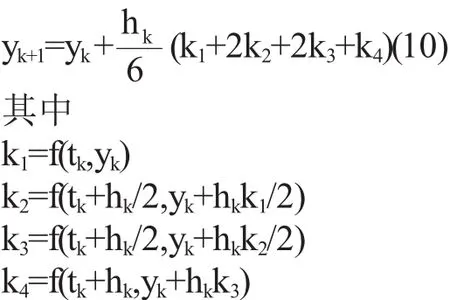
四、Runge-Kutta方法在Matlab語言中的應用

下面以常用的ode45為例講解：

其調用格式為：[t,y]=ode45(odefun,tspan,y0)其中，odefun為用以表示的函數句，為標量，y為標量或向量；tspan如果是二維向量[t0,tf]，表示自變量初值和終值；如果是高維向量[t0,t1,…,tn]，則表示輸出節點列向量；y0表示節點列向量t=(t0,t1,L,tn)T；y表示數值解矩陣，每一列對應y的一個分量；若無輸出參數，則作出圖形。

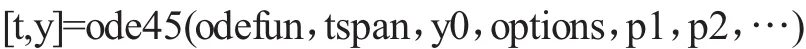
其中，options為計算參數，默認可用空矩陣[]表示；p1,p2,…為附加傳遞參數，這時odefun的表示為f(t,y,pl,p2,L)。

運行程序輸出和的關系。

Runge-kutta法有利于解決數學中的許多實際微分初值問題，方便、易操作，而且圖像處理清晰明了。Runge-kutta法是聯系數學與實際問題的橋梁，能夠較高精度地數值模擬數學建模所建立的微分方程，其計算與實驗結果吻合較好。這種方法能夠解決的問題越來越多，越來越復雜，在微分方程數值求解方法中扮演著非常重要的角色。

五、Runge-kutta法的意義

［1］戴嘉尊，邱建賢.微分方程數值解法［M］.南京:南京出版社，2002.

［2］何強，何英.MATLAB擴展編程［M］.北京：清華大學出版社，2002.

［3］趙靜，但琦.數學建模與數學實驗（第2版）［M］.北京：高等教育出版社，2003.

［4］江世宏.MATLAB語言與數學實驗［M］.北京：科學出版社，2006.

［5］董振海.精通MATLAB 7編程與數據庫應用［M］.北京：電子工業出版社，2007.

O1

A

1673-0046（2011）01-0189-02