用尋找“最小單元”的方法解答2014年江蘇高考第14題

高 尚

（天祝一中，甘肅 天祝 733299）

題目.某裝置用磁場控制帶電粒子的運動，工作原理如圖1所示，裝置的長為L，上下兩個相同的矩形區域內存在勻強磁場，磁感應強度的大小為B，方向與紙面垂直且相反，兩磁場的間距為d.裝置右端有一收集板，M、N、P為板上3點，M位于軸線OO′上，N、P分別位于下方磁場的上下邊界上，在紙面內，質量為m，電荷量為-q的粒子以某一速度從裝置左端中點射入，方向與軸線成30°角，經過上方的磁場區域一次，恰好到達P點，改變粒子入射速度的大小，可以控制粒子到達收集板上的位置，不計粒子的重力.

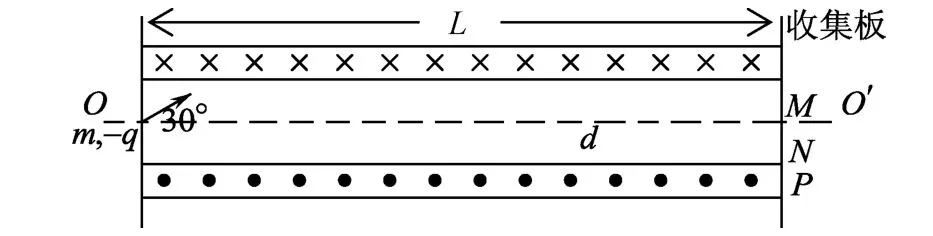
圖1

（1）求磁場區域的寬度；

（2）欲使粒子到達收集板的位置從P點移到N 點，求粒子入射速度的最小變化量Δv；

（3）欲使粒子到達M點，求粒子入射速度大小的可能值.

解析：帶電粒子在勻強磁場做圓周運動時，洛倫茲力提供向心力，物理關系非常簡單，難在幾何構圖和幾何圖形的動態變化.

（1）如圖2所示，粒子從左端中點A射入，先沿直線運動到上方磁場的下邊界B點，進入上方磁場后沿圓弧經最高點C從D點離開上方磁場，然后又沿直線經過與軸線的交點E進入下方磁場的上邊界F點，在下方磁場中沿圓弧到達收集板上的P點.由于對稱性，粒子在運動中表現出“反反復復，繞來繞去”的特點，這就啟發我們去尋找一個“最小單元”，把粒子整體的運動看成是對“最小單元”的多次“復制”或“循環”.

圖2

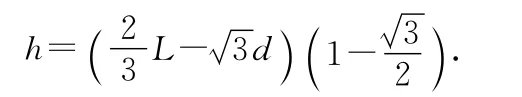
（2）如圖3所示，當粒子的速度略微減小時，它在磁場中的弧長相應減少，就能使其到達收集板的位置從P點移到N 點.設此時粒子在磁場中軌道半徑為r′，“最小單元”沿軸線方向的長度相應變為（dcos30°＋r′sin30°），整體要經過3.5個“最小單元”，據此列出方程L＝3.5（dcos30°＋r′sin30°）.比較圖2和圖3可知運動路線的直線部分沒有變化，而圓弧部發生變化，即圓弧沿軸線方向長度由3rsin30°變為4r′sin30°，列出更簡單的方程 3rsin30°＝4r′sin30°，解出r′后，結合和，解得

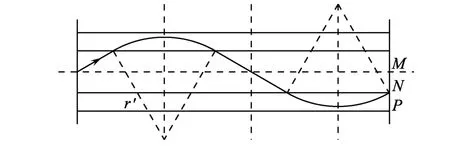
圖3

（3）當粒子的速度進一步減小，但仍然能夠到達M點時，分為兩種情況：一為粒子從下方磁場射向M，如圖4所示；一為粒子從上方磁場射向M，如圖5所示.將兩種情況合并起來，設粒子經過磁場n次，第n次所對應的半徑和速度分別為rn和vn，此時“最小單元”沿軸線方向的長度變為（dcos30°＋rnsin30°），且每經過兩次“最小單元”就一定到達軸線上，因而幾何關系變為L＝n×2（dcos30°＋rnsin30°）.隨著rn越來越小，粒子在磁場中運動的回合越來越多，由于v＝而粒子不能靜止，因此，r只能大nn于0而不能等于0.當rn＞0時，L＞n×2dcos30°，即n＜.所以入射速度的可能值為，n 取整數 ）.當n為奇數時，粒子離開上方磁場射向M；當n為偶數時，粒子離開下方磁場射向M.

感悟：本題沒有過多的數學運算，卻有濃郁的物理氣息，意境深遠，耐人尋味.三問的設置有一種漸入佳境，曲徑通幽之感.考生只要做到準確作圖，步步推進，是能夠完成的.帶電粒子在勻強磁場中的圓周運動與多過程和對稱性相結合的題目，往往存在一個“最小單元”.通過尋找和確定“最小單元”能將這類題目化整為零，從而以小見大，在有效降低難度的同時，更能培養學生解題過程中 “大處著眼，小處著手”的良好習慣.

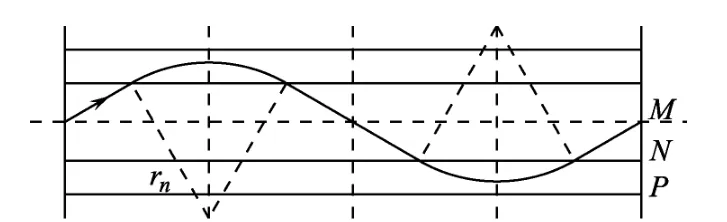
圖4

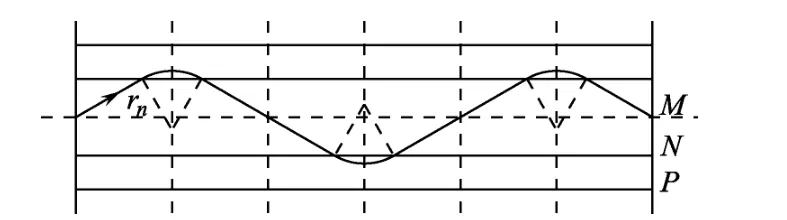
圖5