數學課堂中小組學習的反思

蔣斌

葉圣陶先生說：“教，是為了不教。”這句話既指明了教學的目的，也道出了學生掌握學習方法后的一種理想的學習境界。要做到無師自悟、無師自通，小組學習無疑是一個很好的途徑。學習的方法、學習的內容和討論的時機，這些問題如果處理不當，小組學習就可能失去意義，收效甚微。下面就本人的一些教學實踐，結合課堂教學，談一點膚淺的體會。

小組學習的方法

小組合作學習是在承認課堂教學為基本教學組織形式的前提下，教師以學習小組為重要的教學組織手段，通過指導小組成員展開合作，發揮群體的積極功能，提高個體的學習動力和能力，達到完成特定的教學任務的一種教學方式。素質教育提倡學生主動獲取知識、合作交流，勤于動手，這就必然要求推行“小組合作學習”教學模式。

小組學習的內容

一是安排易混、易錯、易忘概念的小組學習。比如，對易混的概念，像三角形的中位線和中線；易錯的知識點，在解一元一次不等式系數化為1這一步，兩邊都乘以或除以一個負數時，不等號方向忘記改變或結果出錯；對易忘的地方，分式方程應用題的檢驗等。所有這些，教師在講解或讓學生練習時，都可以安排小組進行討論，各抒己見，指出這些地方如何區分，需要注意什么，讓學生自己找出異同，糾正平時作業中的錯誤之處，這樣才能加深學生對數學知識的掌握。

二是完成競爭性作業的小組學習。學生每達到一個要求，教師要有相應的激勵。比如，筆者在講授有理數的加法、乘法和冪的運算時，設置了相關的訓練題，讓每一個小組進行比賽，看誰用的時間短，結果發現，各個小組相當起勁，小組中每個人也毫不示弱，爭先恐后地搶著回答。不僅鞏固了所學的知識，而且也有效地調動了學生的學習積極性。

小組討論的時機

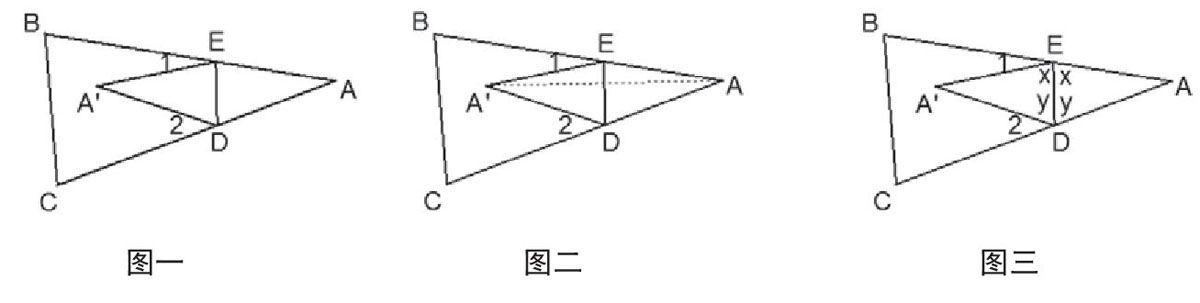
即在學生思考出現困難時進行小組學習。在討論過程中，要展示思維的過程，掌握原理，可消除對數學知識的陌生感，有效激發學生的興趣。以七年級下冊《平面圖形的認識（二）》中復習鞏固第18題的教學情況為例。原題：如圖（1），將△ABC紙片沿DE折疊，使點A落在四邊形BCDE內點A′的位置，探索∠A與∠1+∠2之間的數量關系，并說明理由。

筆者在講解本題時，先叫學生獨立思考，之后再提問，結果發現好多學生都不知如何入手。由于∠1、∠2與∠A不在同一個三角形中，不知道如何聯系起來，這時筆者采取了分組討論，結果好幾個小組很快就把結果探索出來了，歸結起來，有以下三種。

第一種：如圖一，因為四邊形A′DAE的內角和是360°，于是可得∠A′+∠A=360°-（∠A′EA+∠A′DA），根據∠1+∠AEA′=180°，∠2+∠A′DA=180°有∠1=180°-∠AEA′，∠2=180°-∠A′DA，故有∠1+∠2=360°-（∠AEA′+∠A′DA），由等量代換可得∠A′+∠A=∠1+∠2，利用圖像翻折有：∠A′=∠A，因此得到2∠A=∠1+∠2。

第二種：如圖二，連接AA′，根據圖像翻折得：∠EA′A=∠EA A′，由三角形的外角∠1=∠EA′A+∠EA A′，故∠1=2∠EA A′，同樣道理可得到∠2=2∠A′AD， 因此有∠1+∠2=2（∠EAA′+∠A′AD）=2∠EAD。

第三種：如圖三，設∠AED=x，∠ADE=y，根據圖像翻折得：∠A′ED=x，∠A′DE=y，所以∠1=180°-2x，∠2=180°-2y，于是有∠1+∠2=360°-（2x+2y）=360°-2（x+y），另外在△ADE中， x + y =180°-∠A，故有∠1+∠2=2∠A。

通過小組學習，使學生體會了數學試題的解答方法的多樣性，就以上試題來說，第一種是采用三角形內角和與補角知識，第二種采用三角形外角知識，第三種用方程思想，借助整體代換來解決。這三種方法一講出，不僅能從他人的回答中增加自己的見識，而且也讓很多學生體會到了解決數學問題的思考過程，有效地提高了教學效果。

實踐與反思

在實踐過程中，小組學習帶來的優點很多。其一，學生的課堂學習方式明顯改變，學習積極性也在不斷加強，學生能夠根據自己的特點充分發揮自己的優點，在學習數學的過程中感受并體現自己的價值，進而提高了學習數學的積極性。其二，以“優”幫“差”。在小組合作學習過程中，學習成績好的學生會在小組評價的客觀要求下主動幫助那些學習成績差的學生。同時，成績好的學生在小組合作學習中可能會經常扮演教師的角色，充當小先生，角色的轉變要求這些小先生更加深刻地理解所要掌握的教學內容，同樣也是受益匪淺。

（作者單位：江蘇省昆山市玉山中學）