完全信息多目標(biāo)博弈均衡解的存在性

張 杰，李 晗，胡 鼎

（東北電力大學(xué) 理學(xué)院，吉林 吉林132012）

多目標(biāo)博弈也稱為具有向量支付的博弈［1］.現(xiàn)實生活中大部分多目標(biāo)決策問題都存在相互取舍的關(guān)系，因此，多目標(biāo)博弈的研究已成為解決現(xiàn)實博弈問題的主要方法，而均衡解［2］的存在性是多目標(biāo)博弈研究的熱點問題之一［3－5］，目前已受到人們廣泛關(guān)注.文獻(xiàn)［6］討論了相互沖突的多目標(biāo)決策和非合作博弈問題；文獻(xiàn)［7］應(yīng)用集值理論討論了以兩個局中人對抗為主體、多個局中人間接參與的一類特殊微分對策，給出了其極小極大控制的存在性定理；李金澤等［8］將求解單目標(biāo)博弈平衡點的Fan－Glicksberg不動點定理應(yīng)用到對多目標(biāo)博弈平衡點存在性的研究中；文獻(xiàn)［9］對博弈實例進(jìn)行了均衡解的求解；文獻(xiàn)［10－11］分別討論了支付函數(shù)為向量形式的n人非合作多目標(biāo)博弈及不確定參數(shù)變化范圍假設(shè)下的弱Pareto－Nash平衡點的存在性問題，其中后者減弱了多目標(biāo)博弈平衡點存在性定理中策略空間的緊性和支付函數(shù)的凸性等條件.本文通過建立多目標(biāo)博弈模型，給出相應(yīng)的博弈均衡解概念，并對完全信息下多目標(biāo)博弈均衡解的存在性及其性質(zhì)進(jìn)行了研究.

1 完全信息下的多目標(biāo)博弈模型及均衡解

1.1 完全信息下的多目標(biāo)博弈模型

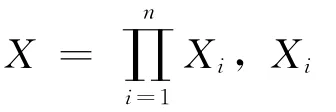
本文基于字典序?qū)δＰ停∕P）進(jìn)行研究.為此，需要對每個支付目標(biāo)函數(shù)確定期望值.

下面不妨將K個支付目標(biāo)函數(shù)劃分為K個優(yōu)先等級，其中第k個支付函數(shù)fik（x）為第k個優(yōu)先級.

1.1.3 基于字典序的整個博弈系統(tǒng)多目標(biāo)博弈模型 對于整個博弈系統(tǒng)，包含n個局中人以及n×K個支付函數(shù)，其字典序極小化的多目標(biāo)博弈模型（P0）如下：求x∈X，使得

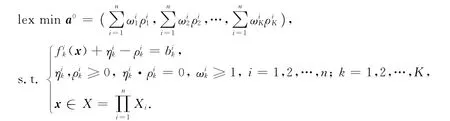
1.1.4 每個局中人的多目標(biāo)博弈模型 對于局中人i，有K個支付函數(shù)，則描述其決策過程的字典序極小化多目標(biāo)博弈模型（Pi）（i＝1，2，…，n）為：求x∈X，使得

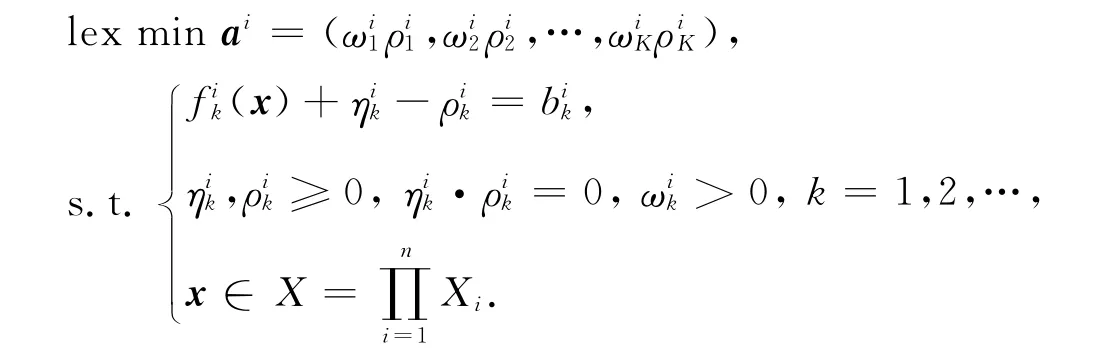
1.1.5 n個局中人合作的多目標(biāo)博弈模型 若n個局中人合作，則表明風(fēng)險共擔(dān)，資源、利益共享.此時，相當(dāng)于整個博弈系統(tǒng)只有一個局中人，其字典序極小化的多目標(biāo)博弈模型（P）為：求x∈X，使得

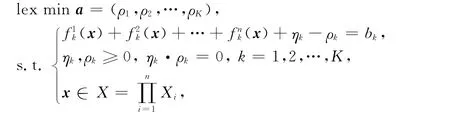
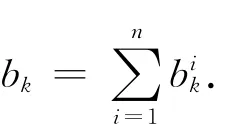
1.2 完全信息下多目標(biāo)博弈均衡解的概念

定義1［12］設(shè)有K 維有序非負(fù)向量a（1），a（2）和a，其中：模型（Pi）和（P）可知，

定義3 模型（P0）的最優(yōu)解稱為完全信息下n個局中人多目標(biāo)博弈系統(tǒng)的偏好均衡解，偏好均衡集記為A（P0）.

定義4 模型（P）的最優(yōu)解稱為完全信息下n個局中人多目標(biāo)博弈系統(tǒng)的合作均衡解，合作均衡集記為A（P）.

2 完全信息下n人多目標(biāo)博弈系統(tǒng)字典序均衡解存在的充分條件

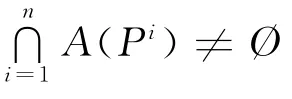
引理1 AL（Pi）＝A（Pi）.

由定義2易證引理1的結(jié)論，故略.

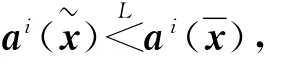
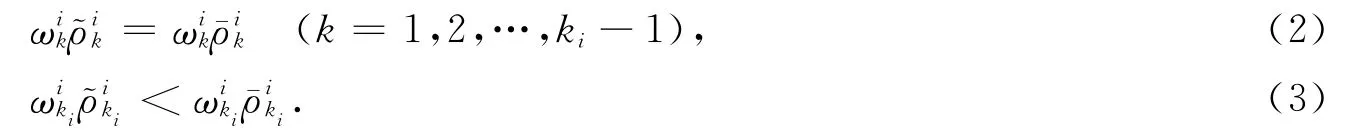
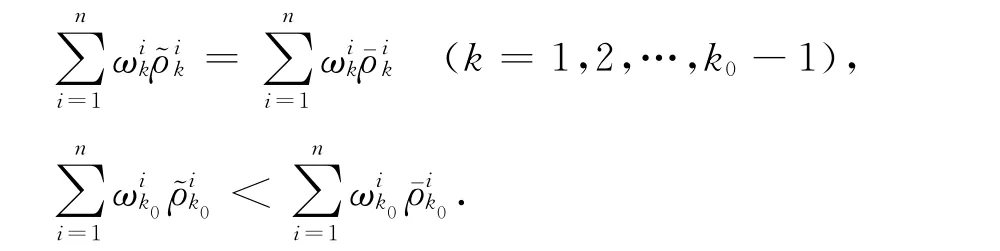
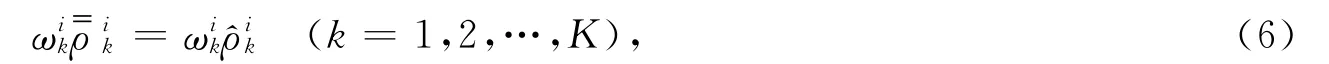
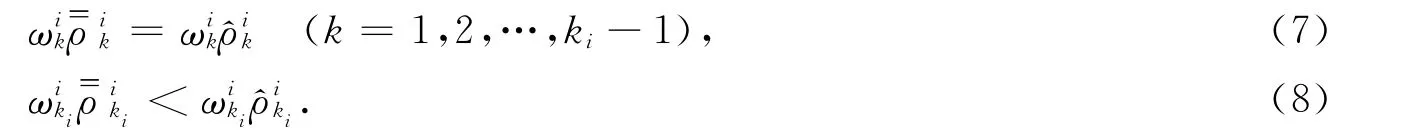
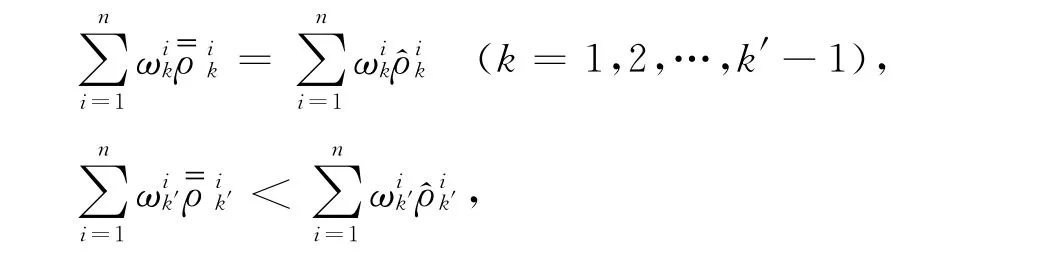
引理2表明，如果每個局中人的多目標(biāo)博弈最優(yōu)策略集的交集非空，則交集中的解即為n個局中人多目標(biāo)博弈模型的偏好均衡解.

定理1表明，如果每個局中人多目標(biāo)博弈最優(yōu)策略集的交集非空，則偏好均衡解即為完全信息下多目標(biāo)博弈系統(tǒng)的字典序均衡解.

3 完全信息下n個局中人多目標(biāo)博弈系統(tǒng)偏好均衡解的性質(zhì)

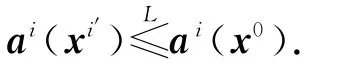
若ai（xi′）＝ai（x0），則有

因此xi′∈A（P0），所以A（Pi′）∩A（P0）≠?，與已知矛盾.若ai（xi′）＜Lai（x0），則有

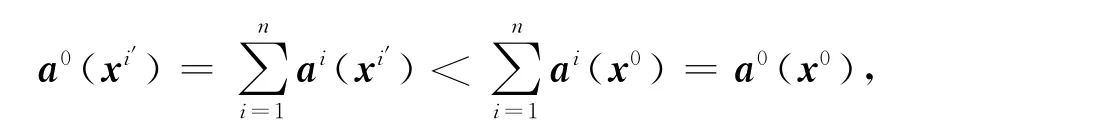
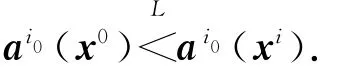
定理2表明，如果模型（P0）中的偏好均衡解不是任意局中人i的字典序均衡解，則對每個局中人i，必存在局中人i0（i0≠i），i0更傾向于選擇系統(tǒng)的偏好均衡解，而不愿選擇局中人i的字典序均衡解.

4 偏好均衡解與合作均衡解的關(guān)系

引理3表明字典序具有傳遞性.

由模型（P）可知

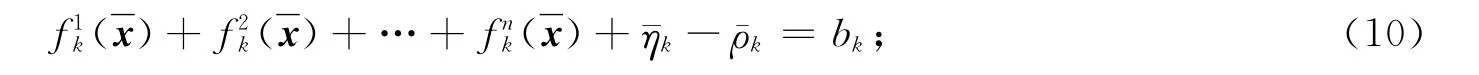
由模型（P0）可知

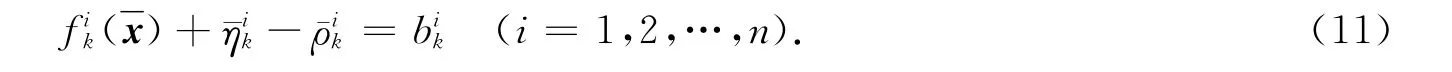
從而由式（11）有

且

由式（10），（12），得

從而由式（13），（14），（16），有

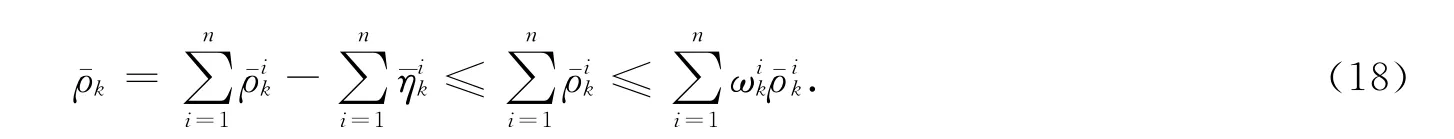
又由式（13），（14），（18），得

定理3表明，若從n個局中人總體利益出發(fā)，選擇合作多目標(biāo)模型（P）所得到的合作均衡解將不劣于選擇n個局中人多目標(biāo)博弈模型（P0）所得到的偏好均衡解.

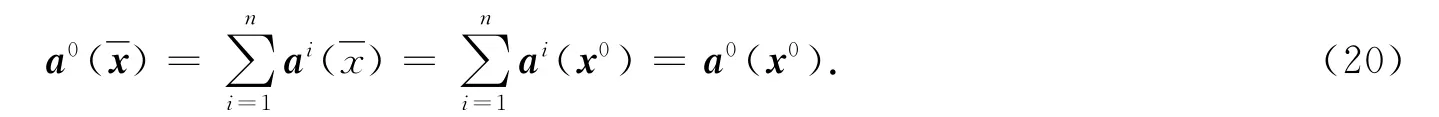
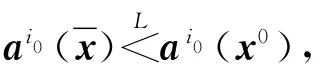
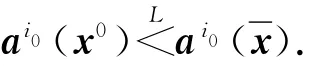
定理4表明，若偏好均衡解集與合作均衡解集不交，則存在局中人i0，他選擇模型（P0）得到的偏好均衡解將不劣于選擇模型（P）中的合作均衡解，即i0更傾向于選擇偏好均衡解.

［1］肖條軍.博弈論及其應(yīng)用 ［M］.上海：上海三聯(lián)書店，2005：17－18.

［2］Shapley C U，Mandayam N B，Goodman D J.Efficient Power Control via Pricing in Wireless Data Networks［J］.IEEE Transactions on Communications，2002，50（2）：291－303.

［3］Ansari Q H，Khan Z.On Existence of Pareto Equilibria for Constrained Multiobjective Games［J］.Southeast Asian Bulletin of Mathematics，2004，27（9）：937－982.

［4］YANG Hui，YU Jian.Unified Approaches to Well－Posedness with Some Applications［J］.Journal of Global Optimization，2005，31（3）：371－381.

［5］Novak A J，F(xiàn)eichtinger G，Leitmann G.A Differential Game Related to Terrorism：Nash and Stackelberg Strategies［J］.J Optim Theory Appl，2010，144（3）：533－555.

［6］DONG Yu，HU Xing－xiang，CHEN Jing－xiong.Game Theory Analysis on Multi－objective Decision ［J］.Operations Research and Management Science，2003，12（6）：35－39.（董雨，胡興祥，陳景雄.多目標(biāo)決策問題的博弈論方法初探 ［J］.運籌與管理，2003，12（6）：35－39.）

［7］WANG Jun，YANG Xue.Multi－participant Differential Games［J］.Journal of Jilin University：Science Edition，2011，49（2）：233－234.（王珺，楊雪.多方參與下的微分對策 ［J］.吉林大學(xué)學(xué)報：理學(xué)版，2011，49（2）：233－234.）

［8］LI Jin－ze，WANG Xun－xiao.Existence Result of Nash Equilibrium Points for Multi－objective Game［J］.Journal of Southwest University for Nationalities：Natural Science Edition，2010，36（4）：547－550.（李金澤，汪訓(xùn)孝.多目標(biāo)博弈Nash平衡點的存在性 ［J］.西南民族大學(xué)學(xué)報：自然科學(xué)版，2010，36（4）：547－550.）

［9］LIN Ci－yun，GONG Bo－wen，ZHAO Ding－xuan，et al.Interregional Traffic Signal Coordination Control under Sudden Disaster Based on Game Theory［J］.Journal of Jilin University：Engineering and Technology Edition，2011，41（5）：1257－1261.（林賜云，龔勃文，趙丁選，等.基于博弈論的突發(fā)災(zāi)害下區(qū)域間交通信號協(xié)調(diào)控制技術(shù) ［J］.吉林大學(xué)學(xué)報：工學(xué)版，2011，41（5）：1257－1261.）

［10］ZHAO Wei，JIANG Lan－xiang.Generalization of the Existence Theorem of Equilibrium Points for Multiobjective Games［J］.Mathematics in Practice and Theory，2011，41（4）：241－246.（趙薇，蔣嵐翔.多目標(biāo)博弈平衡點存在性定理的推廣 ［J］.數(shù)學(xué)的實踐與認(rèn)識，2011，41（4）：241－246.）

［11］YANG Zhe，PU Yong－jian，GUO Xin－yi.On the Existence of Weakly Pareto－NS Equilibrium Points in Multi－objective Games under Uncertainty［J］.Systems Engineering：Theory ＆ Practice，2013，33（3）：660－665.（楊哲，蒲勇健，郭心毅.不確定性下多目標(biāo)博弈中弱Pareto－NS均衡的存在性 ［J］.系統(tǒng)工程理論與實踐，2013，33（3）：660－665.）

［12］張杰，郭麗杰，周碩，等.運籌學(xué)模型及其應(yīng)用 ［M］.北京：清華大學(xué)出版社，2012.