一類具分數階積分條件的分數階微分方程組解的存在唯一性

李耀紅，張海燕

（宿州學院 智能信息處理實驗室，安徽 宿州234000）

0 引 言

分數階微積分理論廣泛應用于自然科學和工程技術等領域，目前已成為許多數學工作者的研究熱點［1－6］.分數階微分方程組邊值問題也受到廣泛關注［7－12］.特別地，文獻［7－8］利用Schauder不動點定理分別研究了分數階方程組兩點和三點邊值問題正解的存在性；文獻［9］利用錐拉伸和壓縮不動點定理研究了混合分數階方程組兩點邊值問題正解的存在性；文獻［10］利用重合度理論研究了振動情形下分數階方程組多點邊值問題的可解性.基于此，本文考慮一類具分數階積分邊值條件且包含Caputo型分數階導數的分數階微分方程組邊值問題：

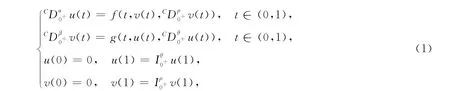
其中：CD0＋是Caputo分數階導數；1＜α，β＜2；0＜ρ，θ＜1；f，g：［0，1］×?×?→?.

與已有結果不同，本文積分邊值條件依賴Riemann－Liouville分數階積分，包含整數積分條件和局部多點邊值條件，因此本文研究的邊值問題（1）更具有一般性.具積分邊值條件的常微分邊值問題廣泛應用于種群動態模型、血液流動模型、熱傳導、化學化工和等離子物理等領域［11－12］.本文首先將問題（1）轉化為等價的積分方程組，獲得了相應的格林函數，然后利用Banach壓縮映射原理，得到了該問題存在唯一解的充分條件，并給出了應用實例.

1 預備知識

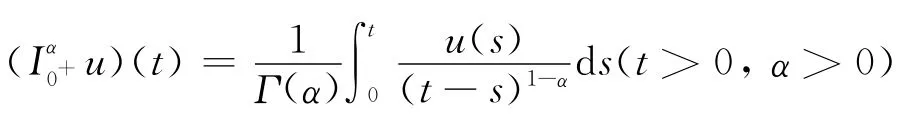
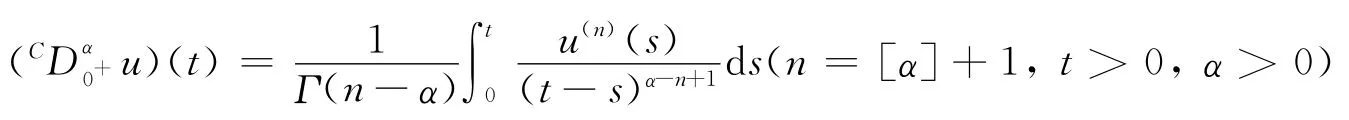
引理1［1］設α＞0，u（t）∈C（0，1），則齊次分數階微分方程u（t）＝0有一般解

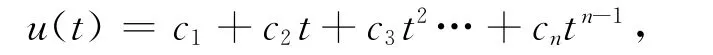
其中ci∈?，i＝1，2，…，n，n＝［α］＋1，［α］表示α的整數部分.

引理2［1］設p＞q＞0，f∈L［a，b］，則對?t∈［a，b］，有

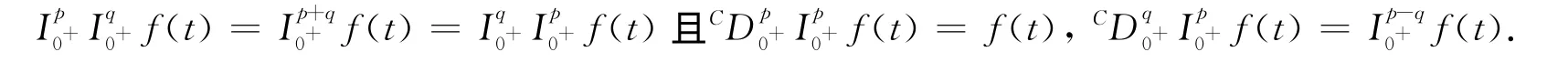
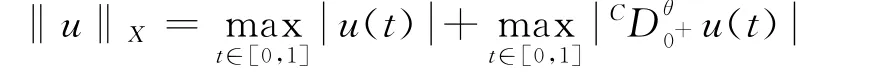
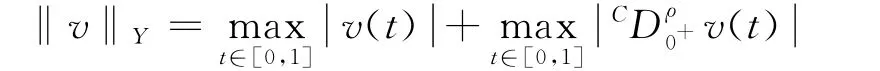
下也是一個Banach空間.顯然，（X×Y，‖·‖X×Y）在范數‖·‖X×Y＝max｛‖u‖X，‖v‖Y｝下是一個Banach空間.

引理3 設1＜α＜2，0＜θ＜1，u（t）∈C（0，1），則分數階微分方程積分邊值問題：

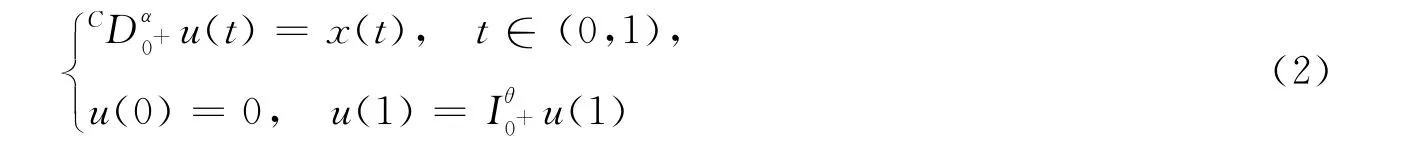
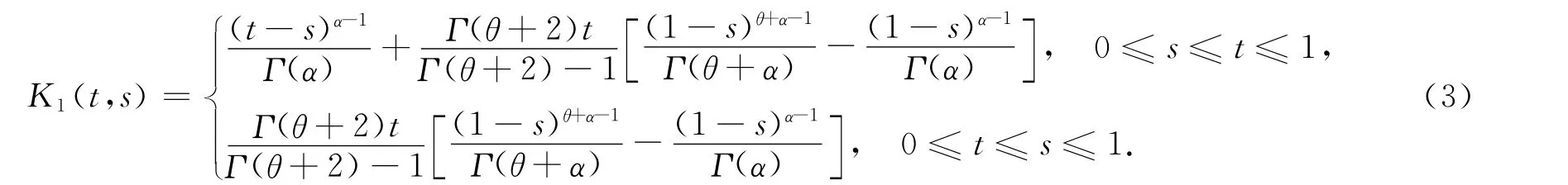
進一步由引理2有

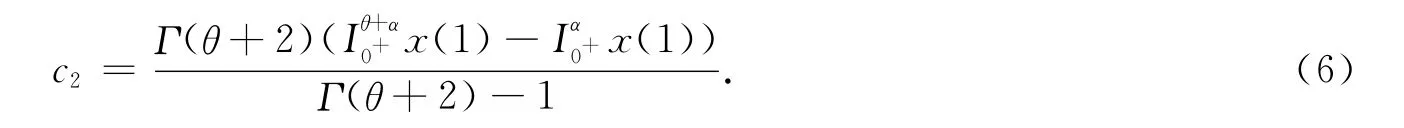
將式（6）代入式（4），有

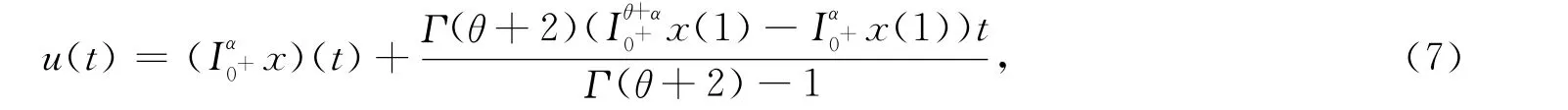
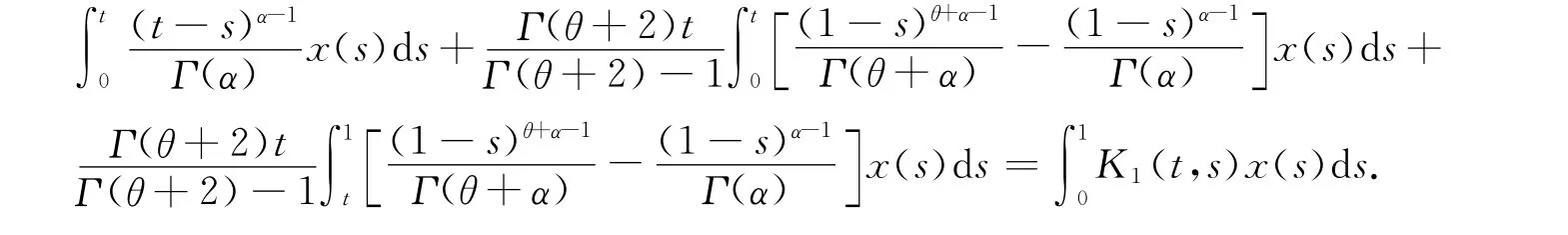
證畢.

同理，邊值問題CDv（t）＝y（t），v（0）＝0，v（1）＝v（1）也有唯一解

其中K2（t，s）通過將K1（t，s）中α置換為β，θ置換為ρ得到.

定義積分算子T：X×Y→X×Y 如下：T（u，v）（t）＝（T1v（t），T2u（t）），其中：

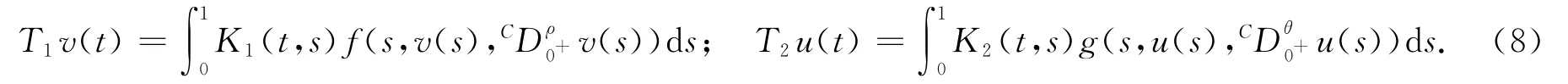
引理4 設f，g∈C（［0，1］×?×?，?），則（u，v）∈X×Y 是分數階微分方程組邊值問題（1）的解當且僅當T（u，v）（t）＝（u，v）（t），?t∈［0，1］.

證明：設（u，v）是邊值問題（1）的解，且令

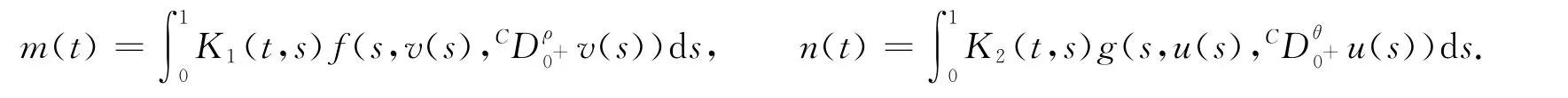
由式（7）知

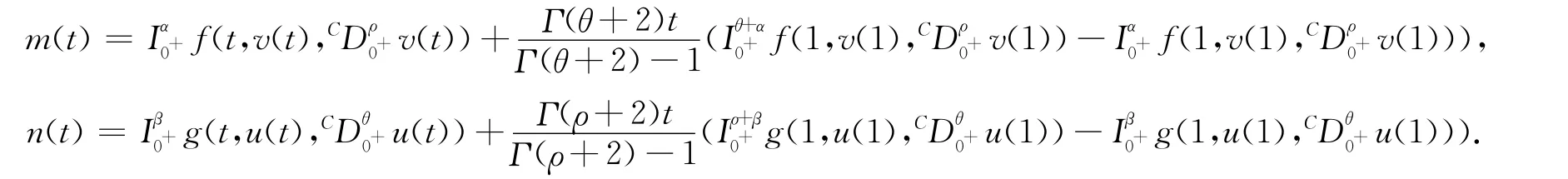
由引理2知

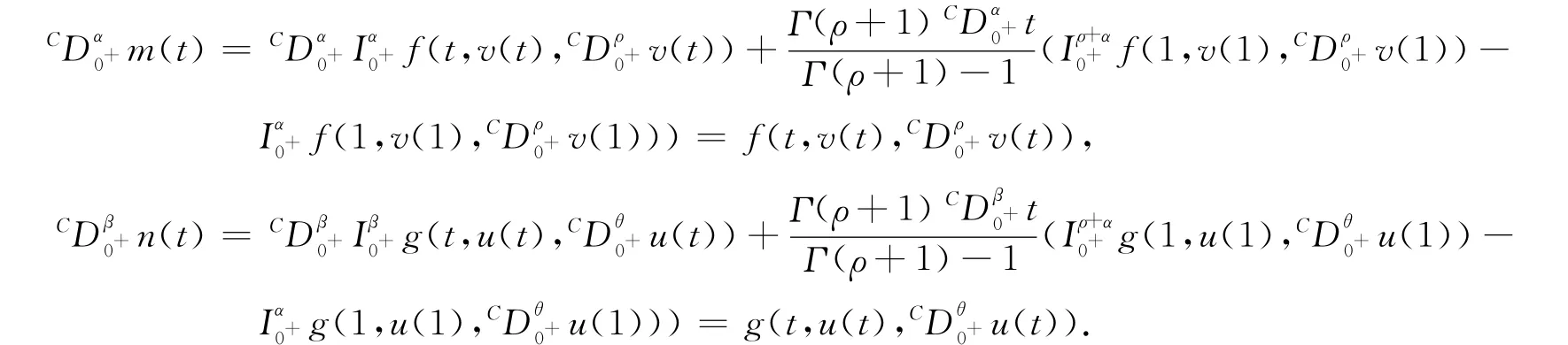
易證（m，n）滿足邊值問題（1）的邊值條件，則（m，n）是邊值問題（1）的解，且（m，n）＝（u，v）.

2 主要結果

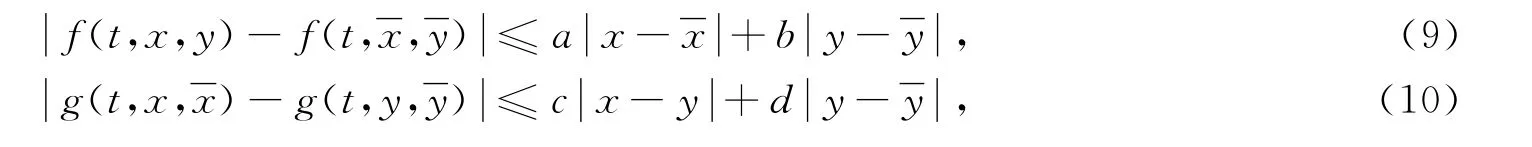
且

則分數階微分方程組邊值問題（1）在X×Y中存在唯一解，其中：

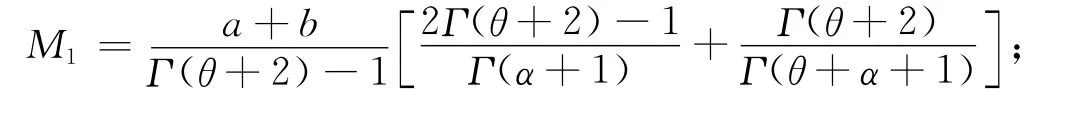
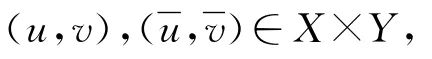
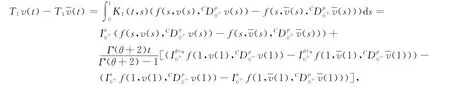
于是，結合條件（9）有

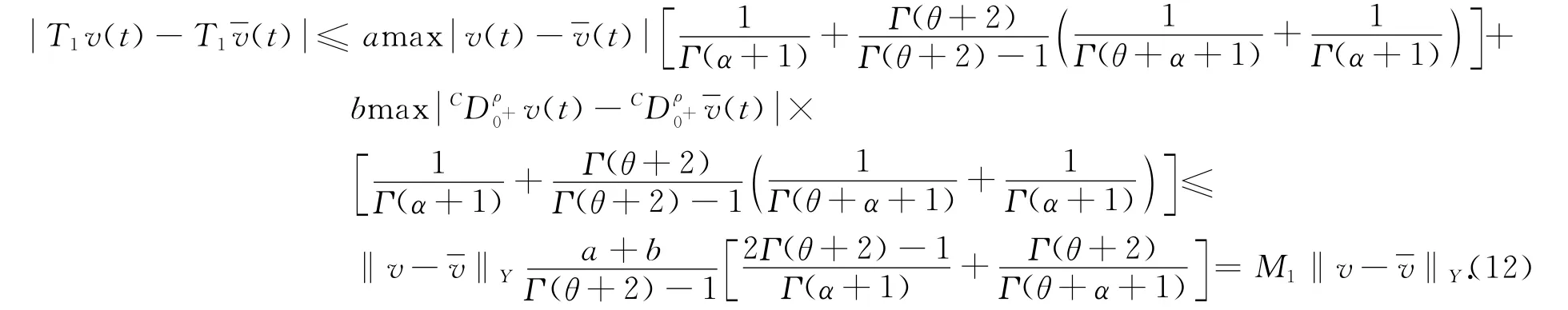
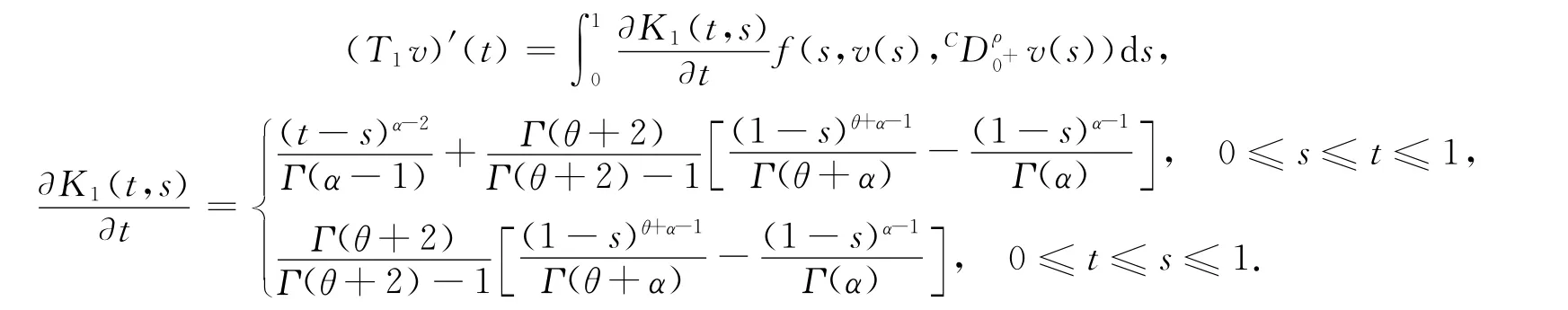
因此

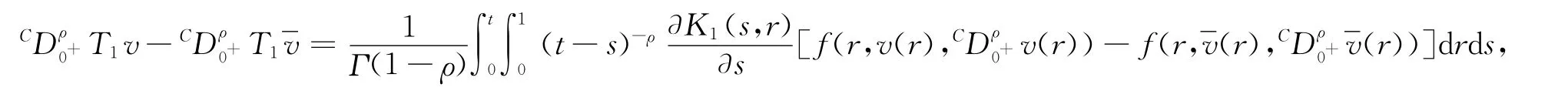
于是，利用假設條件（9）可知

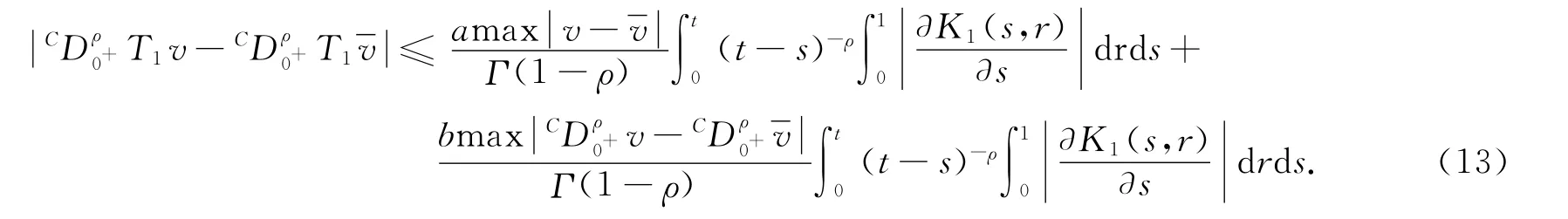
再注意到

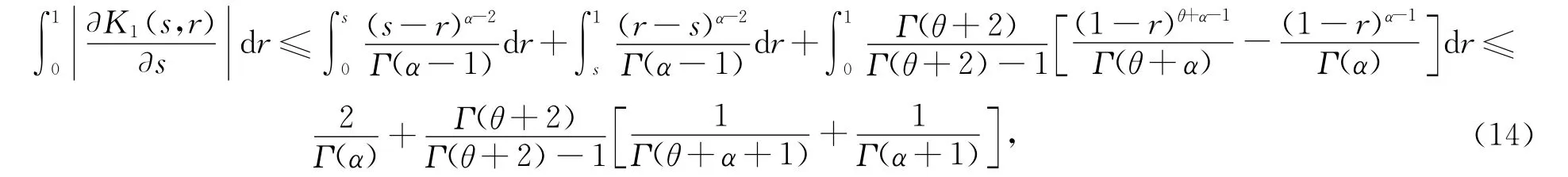
將式（14）代入式（13），則有

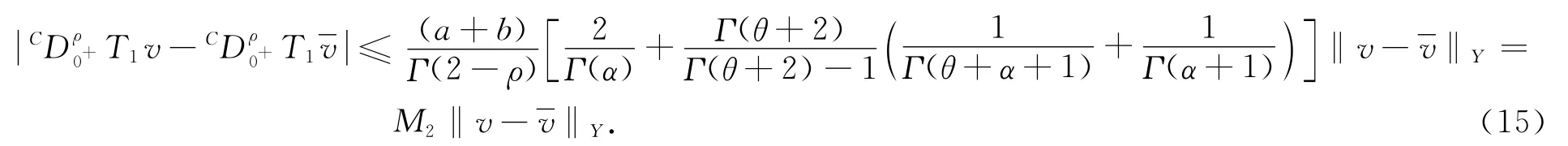
由范數的定義，并結合式（12），（15）知

同理，有

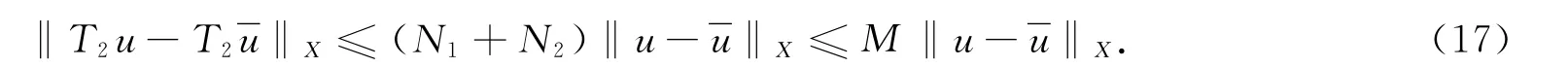
從而由式（16），（17）知

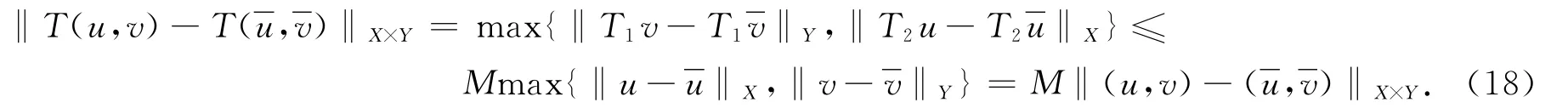
故由式（18）并結合式（11）可知，算子T是一個壓縮映射，因此算子T在X×Y中有一個唯一不動點，即分數階微分方程組邊值問題（1）在X×Y中存在唯一解.

3 應用實例

例1 考慮如下分數階微分方程組邊值問題：

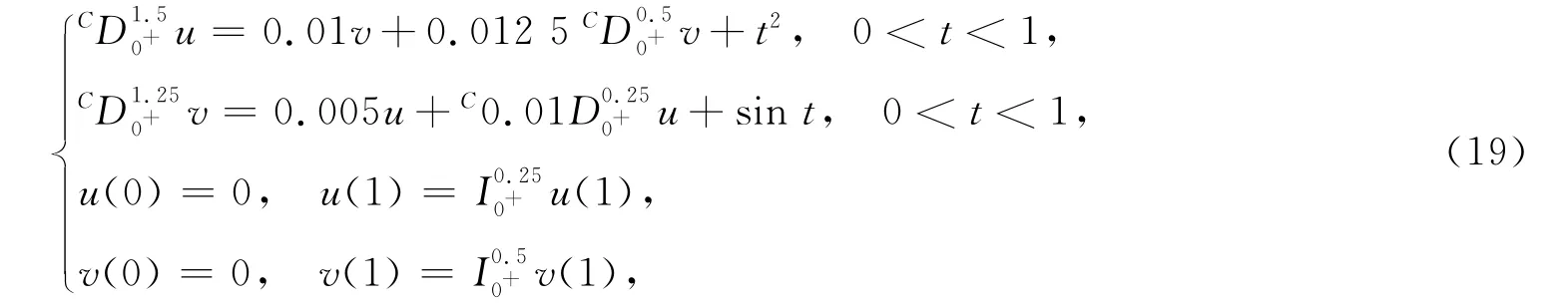
于是f（t，x，y）＝0.01x＋0.012 5y＋t2，g（t，x，y）＝0.005x＋0.01y＋sin t，1＜α＝1.5＜2，1＜β＝1.25＜2，0＜ρ＝0.5＜1，0＜θ＝0.25＜1，則易知a＝0.01，b＝0.012 5，c＝0.005，d＝0.01，從而通過直接計算可得：M1＝0.280 280，M2＝0.354 460，N1＝0.104 323，N2＝0.135 117，M1＋M2＜1，N1＋N2＜1.因此，由定理1可知方程組邊值問題（19）在X×Y中存在唯一解.

［1］Kilbas A A，Srivastava H M，Trujillo J J.Theory and Applications of Fractional Differential Equations［M］.Amsterdam：Elsevier，2006.

［2］Lakshmikantham V，Leela S，Devi J V.Theory of Fractional Dynamic Systems［M］.New York：Cambridge Scientific Publishers，2009.

［3］ZHANG Shu－qin.Positive Solution for Boundary Value Problem of Nonlinear Frctional Differential Equations［J］.Electron J Differ Eq，2006，2006（36）：1－12.

［4］WEI Zhong－li，LI Qing－dong，CHE Jun－ling.Initial Value Problems for Fractional Differential Eequations Involving Riemann－Liouville Sequential Fractional Derivative［J］.J Math Anal Appl，2010，367（1）：260－272.

［5］BAI Zhan－bing.Solvability for a Class of Fractional m－Point Boundary Value Problem at Resonance［J］.Comput Math Appl，2011，62（3）：1292－1302.

［6］YANG Xiong，WEI Zhong－li，WEI Dong.Existence of Positive Solutions for the Boundary Value Problem of Nonlinear Fractional Differential Equations［J］.Commun Nonlinear Sci Numer Simul，2012，17（1）：85－92.

［7］SU Xin－wei.Boundary Value Problem for a Coupled System of Nonlinear Fractional Differential Equations［J］.Appl Math Lett，2009，22（1）：64－69.

［8］Ahmada Bashir，Nieto J J.Existence Results for a Coupled System of Nonlinear Fractional Differential Equations with Three－Point Boundary Conditions［J］.Comput Math Appl，2009，58（9）：1838－1843.

［9］ZHAO Yi－ge，SUN Shu－rong，HAN Zhen－lai，et al.Positive Solutions for a Coupled System of Nonlinear Differential Equations of Mixed Fractional Orders［J］.Advances in Difference Equations，2011，2011（1）：64－69.

［10］JIANG Wei－hua.Solvability for a Coupled System of Fractional Differential Equations at Resonance［J］.Nonlinear Anal，2012，13（5）：2285－2292.

［11］YANG Wen－gui.Positive Solutions for a Coupled System of Nonlinear Fractional Differential Equations with Integral Boundary Conditions［J］.Comput Math Appl，2012，63（1）：288－297.

［12］JIANG Ji－qiang，LIU Li－shan，WU Yong－hong.Multiple Positive Solutions of Singular Fractional Differential System Involving Stieltjes Integral Conditions［J］.Electron J Qual Theory Differ Eq，2012，2012（43）：1－18.