一種基于全變差正則化與小波包變換的圖像去噪算法

左 平，王 洋，申延成

（1.空軍航空大學 基礎部，長春130022；2.吉林大學 計算機科學與技術學院，長春130012；3.吉林大學 公共計算機教學與研究中心，長春130012）

圖像去噪是指利用各種方法從已知的含噪圖像中去除噪聲部分，同時盡可能保留圖像邊緣等細節特征.傳統的圖像去噪方法主要有小波變換算法［1］、基于小波變換的軟閾值圖像去噪算法［2］和小波包分析［3］方法等.但上述方法都存在一定的缺陷.

Rudin等［4］基于全變差（TV）極小化的思想，提出一種具有很好去噪效果的方法，即經典的ROF方法，該方法在去除噪聲的同時能很好地保護圖像的邊緣.Marquina等［5］對TV去噪模型提出了進一步的改進方法.Chan等［6］提出將偏微分方程方法應用于基于小波的圖像處理中，使得經小波硬閾值處理后的圖像在邊緣處產生的振蕩得到抑制，但紋理也被作為噪聲平滑掉了.同時，全變差極小化的方法也用于解決 Ridgelet復原［7］、Curvelet復原［8－9］和 Tetrolet復原［10］中的邊緣保持問題.

1 去噪算法的數學模型

由于噪聲和圖像的細節特征主要集中于圖像高頻部分，因此在對圖像進行去噪過程中，常會使圖像的某些重要特征（如邊緣、細小紋理等）受到破壞.對于加性噪聲模型：

基于全變差極小化的思想，提出以下去噪模型：

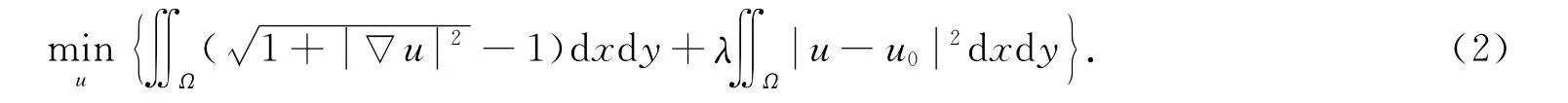
式（2）中第一項稱為正則項，它通過控制TV范數保護圖像的邊緣特征，有平滑圖像的作用；第二項稱為逼近項，它控制圖像u（x，y）和u0（x，y）的逼近程度，有使圖像去噪前后差別不大的作用；正則化參數λ有調節逼近項的作用，當λ充分大時，可知模型中第二項起決定作用，而當λ→0時，第一項控制整個目標函數，此時u（x，y）趨于一常值.因此在求解時參數λ的選取十分重要.

利用變分法得到式（2）相應的Euler－Lagrange方程為

對方程（3）可采用固定點迭代方法［11］或時間演化法［4］求解.若采用時間演化法，則相應的偏微分方程為

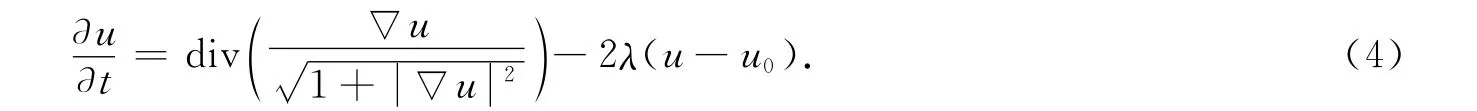
在Rudin等［4］提出的ROF去噪模型中，正則化參數λ的選取與初始加入的噪聲方差有關，相應的λ表達式為

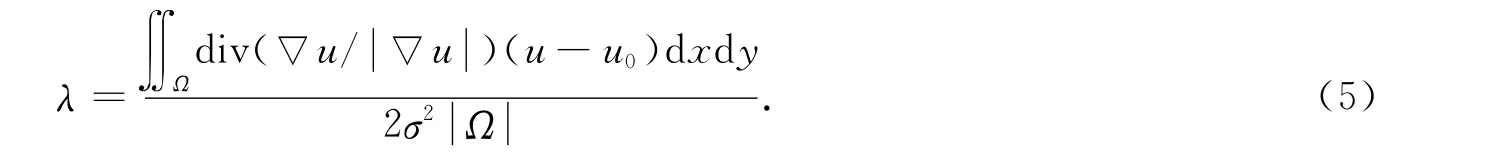
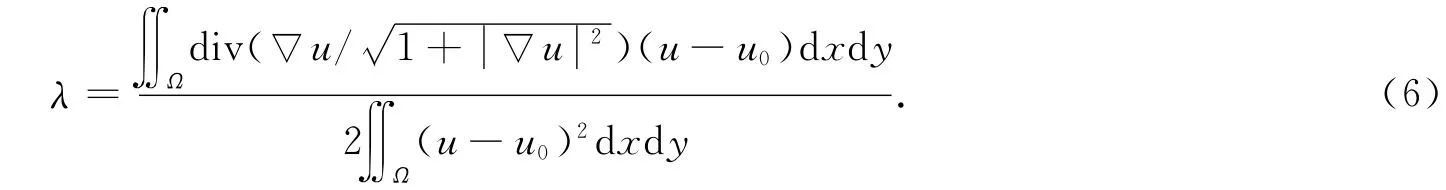
從而可適當避免參數λ取值偏小導致模型（2）中的正則項作用過大，進而導致圖像中某些細微邊緣被平滑處理掉.

2 去噪模型的數值解法

根據建立的數學模型，下面給出基于小波包與全變差模型的圖像去噪算法.步驟如下：

1）先利用小波包變換，對含噪圖像u0（x，y）進行4層分解；再根據選定的信息代價函數尋找最優小波包基并對最優小波包基下對應的小波包系數進行軟閾值［3］處理；利用處理后的系數重構圖像，得到初步去噪后的圖像u1（x，y）；

2）根據式（6）選取正則化參數λ；

3）將方程（4）進行展開并化簡：

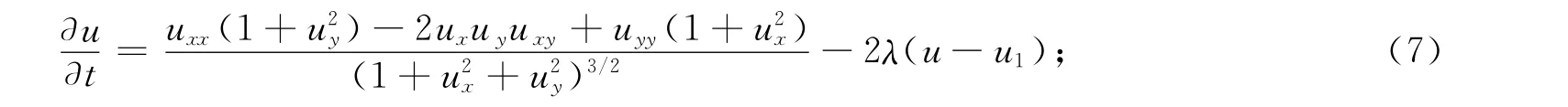
4）給出方程（6），（7）的離散格式，并進行迭代求解：

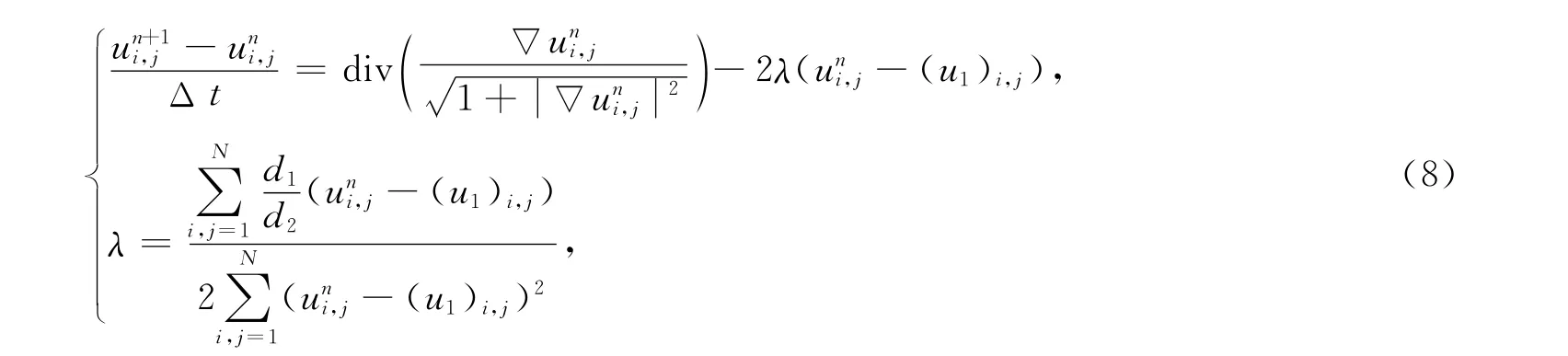
其中

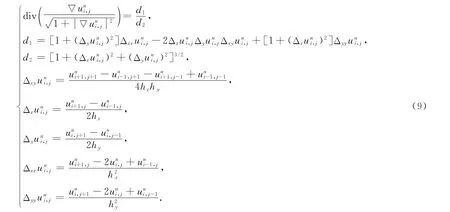
算法根據去噪前后圖像的能量差確定迭代停止時刻：

其中：un為第n次迭代結果；ε0為一任意小的常數.把滿足上述條件的時刻作為迭代停止時刻.

3 實驗結果分析

本文仿真平臺軟件環境為Matlab 7.14；硬件環境為Intel i7－2630QM＠2.0GHz，內存4Gb.為驗證去噪算法的有效性，將本文方法（total variation based on wavelet packet，TVWP）與TV小波閾值去噪法（total variation based on wavelet thresholding，TVW）［6］、小波軟閾值去噪法（wavelet soft thresholding，WST）［2］和 ROF去噪法［4］進行對比實驗，以峰值信噪比（peak signal to noise ratio，PSNR）、結構相似性指數（structural simiiarity index，SSIM）［12］和算法運行時間（單位：s）作為衡量指標.實驗選取256×256的灰度標準測試圖像Lena，Cameraman，Woman和Fruits.噪聲類型為加性高斯白噪聲，噪聲標準差σ＝15.實驗中時間步長Δt＝0.1，閾值ε＝15，網格步長hx＝hy＝1.為定量比較各種不同去噪算法的效果，表1列出了各種去噪算法去噪的定量對比結果.

表1 不同算法在標準測試圖像上的去噪結果Table 1 Results of denoising via different algorithm on standard test images

圖1～圖4分別為不同算法在不同測試圖像上的去噪結果.由圖1～圖4可見，ROF方法去噪結果中存在塊效應，且圖像中的細節信息被破壞了.表明將ROF方法直接應用于噪聲圖像，易發生誤將噪聲作為圖像的邊緣處理，從而導致圖像的平坦區域出現塊效應現象.在算法運行過程中，λ取為定值，導致隨著算法迭代次數的增加，圖像的細節信息被破壞，不能達到較好的去噪效果.而本文方法利用小波包變換的優點，對含噪圖像進行預處理，避免了去噪后圖像產生塊效應的現象；又因小波包變換可以對圖像高頻信息進行更精細的劃分，使得在去噪過程中更好地保護了圖像中的細節信息，之后再對預處理后的圖像使用全變差方法去噪，可以得到更好的視覺效果.由表1可見，小波軟閾值方法與TV小波閾值方法的PSNR值相當，本文算法的PSNR值有所提高，約提高1dB.

圖1 不同算法在Lena圖像上的去噪結果Fig.1 Results of denoising via different algorithm on Lena image

圖2 不同算法在Cameraman圖像上的去噪結果Fig.2 Results of denoising via different algorithm on Cameraman image

圖3 不同算法在Woman圖像上的去噪結果Fig.3 Results of denoising via different algorithm on Woman image

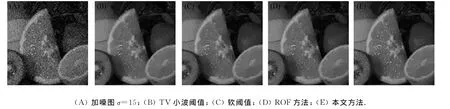
圖4 不同算法在Fruits圖像上的去噪結果Fig.4 Results of denoising via different algorithm on Fruits image

綜上，小波包變換和全變差極小化是近年來較廣泛使用的兩種去噪方法，本文通過分析二者各自的特點，提出了一種基于小波包分析和全變差模型的圖像去噪算法，并給出一種改進的正則化參數選擇方法.實驗結果表明，該算法克服了原有方法的不足，在有效抑制圖像噪聲的同時較好地保留了圖像的邊緣和紋理等細節信息.

［1］Mallat S G.A Theory for Multiresolution Signal Decomposition：The Wavelet Representation ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11（7）：674－693.

［2］Donoho D L.De－noising by Soft－Thresholding ［J］.IEEE Transactions on Information Theory，1995，41（3）：613－627.

［3］Ramchandran K，Vetterli M.Best Wavelet Packet Bases in a Rate－Distortion Sense［J］.IEEE Transactions on Image Processing，1993，2（2）：160－175.

［4］Rudin L I，Osher S，Fatemi E.Nonlinear Total Variation Based Noise Removal Algorithms［J］.Physica D，1992，60（1／2／3／4）：259－268.

［5］Marquina A，Osher S J.Image Super－Resolution by TV－Regularization and Bregman Iteration［J］.J Sci Comput，2008，37（3）：367－382.

［6］Chan T F，ZHOU Hao－min.Total Variation Wavelet Thresholding［J］.Journal of Scientific Computing，2007，32（2）：315－341.

［7］MA Jian－wei，Fenn M.Combined Complex Ridgelet Shrinkage and Total Variation Minimization［J］.SIAM J Sci Comput，2006，28（3）：984－1000.

［8］TANG Gang，MA Jian－wei.Application of Total－Variation－Based Curvelet Shrinkage for Three－Dimensional Seismic Data Denoising［J］.IEEE Geosci Remote Sensing Lett，2011，8（1）：103－107.

［9］XIAO Liang，HUANG Li－li，Roysam B.Image Variational Denoising Using Gradient Fidelity on Curvelet Shrinkage［J］.EURASIP Journal on Advances in Signal Processing，2010，2010：398410.

［10］Krommweh J， MA Jian－wei.Tetrolet Shrinkage with Anisotropic Total Variation Minimization for Image Approximation［J］.Signal Processing，2010，90（8）：2529－2539.

［11］Vogel C，Oman M.Iterative Methods for Total Variation Denoising［J］.SIAM J Sci Stat Comput，1996，17：227－238.

［12］WANG Zhou，Bovik A C，Sheikh H R，et al.Image Quality Assessment：From Error Visibility to Structural Similarity［J］.IEEE Trans Image Process，2004，13（4）：600－612.