用條件方程式直接探測多維粗差的方法研究

劉 利，葛永慧

（1.太原市城鄉規劃局 城鄉建設檔案館，太原 030002；2.太原理工大學 礦業工程學院，太原 030024）

粗差是超出觀測值一定限度的誤差，根據偶然誤差的規律性，粗差基本都大于觀測值的三倍中誤差。粗差出現是小概率事件，有時確實也存在，但在觀測值中是極少數的，所以在進行平差計算前，應該進行粗差探測[1]。國內外測量研究人員進行了大量的理論研究，并通過大量實際案例論證，從理論和具體方法上都取得了很多可行的研究成果。通過查閱文獻，這些理論和方法的基本思路一般為兩種情況：一是采用待估參數計算，將粗差作為待估參數直接計算，用擬穩平差的原理解算秩虧問題，然后進行探測粗差；二是將隨機選定含粗差概率小的、有驗證條件的觀測值當成平差計算的起算數據，運用隨機選取的數據進行最小二乘法解算出待估參數，含粗差的概率較大的觀測值，也就是非準觀測值的殘差作為粗差[2]。用第一種思路解決粗差探測問題時，又分為兩種方式，第一是將極少數疑是觀測值（含粗差）和一般觀測值（不含粗差）看成具有相同方差、不同期望的一個基本子樣，即把粗差看作是函數模型的一小部分，用這一方式最早提出一個粗差探測技術的是荷蘭的巴爾達教授（Baarda）[3]；第二是將極少數的疑是觀測值（含粗差）和一般觀測值（不含粗差）看作具有相同方差、不同期望的一個基本子樣，即把粗差當成是隨機模型中的一小部分[4]。研究分析現有粗差探測的方法后不難發現，這些粗差探測的方法一要采用最小二乘法平差原理，進行經典平差解算；二要采用全面搜索、迭代重新平差計算，很多次重復計算后，才能找到粗差。這些方法搜索、迭代的次數比較多，相對運行的時間也比較長。最小二乘法原理存在均攤性的算法缺陷，直接對含有粗差的觀測值進行最小二乘法計算，就會對所有觀測值造成影響，達不到粗差探測的效果。為了避免最小二乘法原理的先天缺陷，筆者提出了一種新思路：將條件方程作為觀測值中粗差探測的起點，把條件方程式閉合差（W）作為是否存在粗差的信號，不再做最小二乘法平差。本方法從思路、實現過程都相對簡單，操作性比較強。

1 條件平差理論下的閉合差協因數陣

按照條件平差原理的數學模型，必要觀測個數為t，觀測值個數為n，多余觀測個數為r＝n-t，列出r個條件方程式，條件平差的數學模型為：

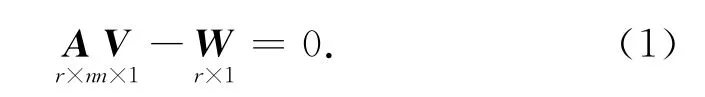
運用最小二乘法原理VΤPV＝min，解算得觀測值的改正數向量V。

由W＝-AL-A0計算出QWW協因數陣是：

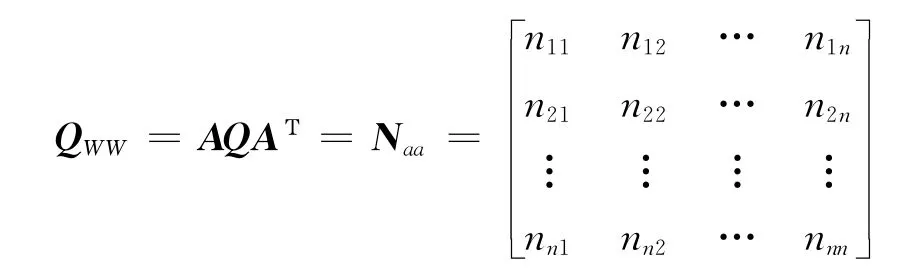
式中：QWW為閉合差W 的協因數陣；Naa為方程系數陣；Q為觀測值的協因數；V為改正數向量；P為權陣；W 為閉合差向量；L為觀測值向量；A0為條件式的常數列向量。

根據偶然誤差理論，閉合差W可取偶然誤差的極限誤差，即2、3倍中誤差。假設W＝2倍的中誤差時，其W限差列向量為：

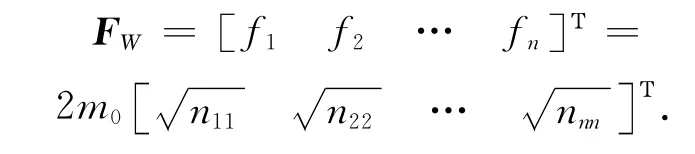
m0表示驗后單位權中誤差。

在相同觀測條件下，在不考慮粗差、系統誤差的情況下，W限差列向量根據偶然誤差理論應服從N（0，m02Qww），即正態分布，即對i都滿足

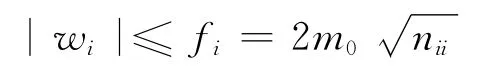
得：W可作為檢驗數學模型（1）成立與否的一個可靠統計值[5]。

2 條件方程式探測多維粗差法

2.1 基本原理

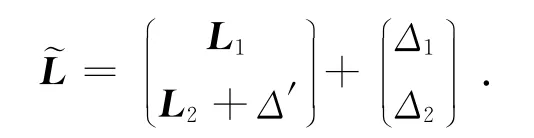
式中：L1，L2為觀測值表示觀測真值；Δ1，Δ2表示真誤差。根據已知數據條件列出解算條件方程為：

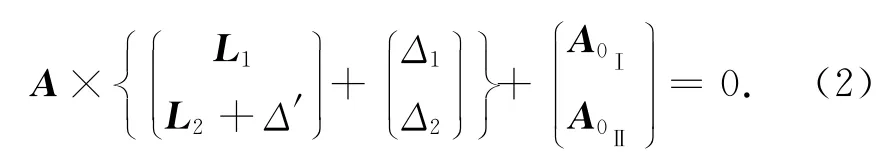
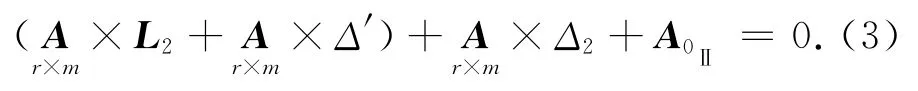
式中：WⅡ為含有粗差閉合差向量，

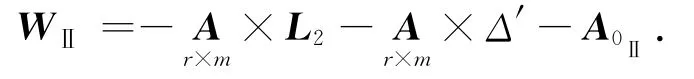
根據平差模型，得出WⅡ中含有粗差的結論。即能夠推斷出，與涉及該閉合差的某些觀測值中含有粗差。而且，粗差也體現在所有含有該觀測值的條件方程的閉合差上。條件方程式探測多維粗差法就是根據這一總結提出來的。

2.2 實現過程

1）根據（1）式建立基礎條件方程式，保存其系數陣A1。

2）根據基礎條件方程式，建立完全條件方程式，保存其系數陣A2。建立完全條件方程式的基本要求為，保證觀測值組成的路線在圖形上是有組合意義的，即保證其路線的閉合性。

3）根據上一步的結果，搜尋閉合差

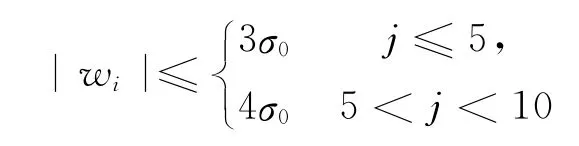
方程式，保存其系數陣A3。j為組成條件方程式的觀測值個數。

4）對A3進行列變換，計算出Z的秩。含有粗差的觀測值數為b＝r-Z.根據A3的秩Z≥1，推斷出b≤r-1，得最多探測出r-1個粗差項。

5）計算A4，為A3的任意一組最大行線性無關組。

6）根據含有粗差的觀測值在A4中的所有列向量為零，確定含有粗差觀測值。

3 算例

1）有一水準網（如圖1所示），高差觀測值個數為n＝6，必要觀測值個數為t＝3，多余觀測值個數為r＝3.分別隨機模擬兩組含有粗差的數據見表1所示。

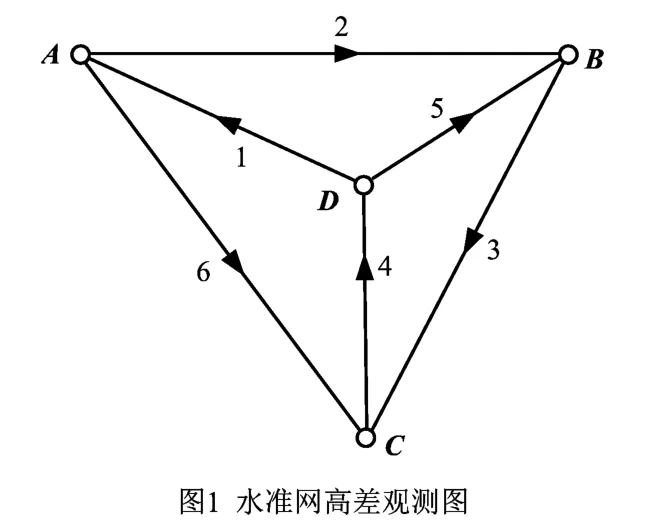
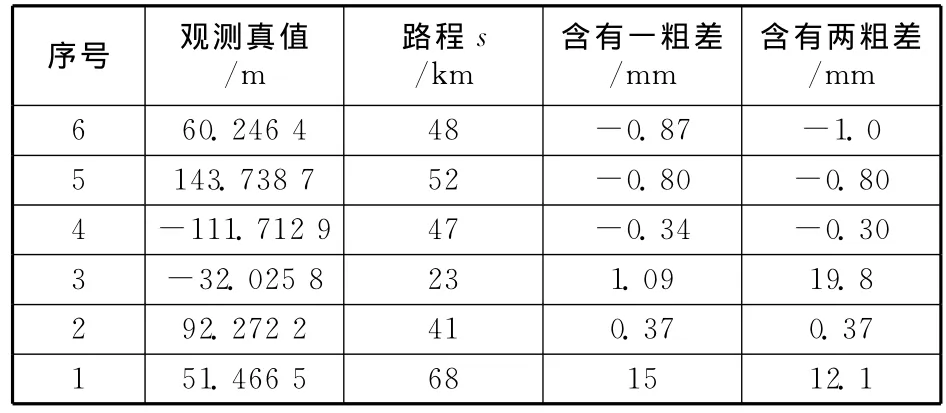
表1 模擬觀測值的基本數據

采用本文方法步驟，首先由計算機自動生成觀測值的偶然誤差，再由

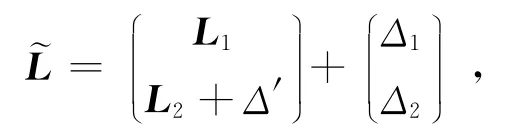
模擬出高差觀測值。對含有一個粗差，且該粗差放在第一條變化的觀測值上的情況進行分析，說明其解算過程。

根據上述方法，首先，計算出A1和A2，再根據

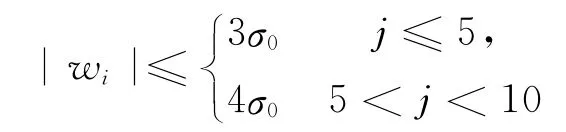
計算出A3，求A3的秩Z＝2。解算粗差個數b＝r-Z＝1。最后得出計算探測結果為第一條邊含有粗差。本次算例的結果完全驗證了筆者提出方法的可靠性。

將模擬粗差放在第一、第三邊的觀測值上，根據該方法的判斷標準，檢驗其模擬結果也完全正確。

綜上所述，筆者所驗證的粗差探測方法，其原理容易理解、計算高效、實現過程簡單，計算次數少、探測粗差效率高，避免了平差計算，也不需要進行反復多次迭代、搜索計算，一次計算就能夠確定出觀測數據中的所有粗差項。

按上述模擬數據方法，僅含一個粗差在各邊上的情況，每種情況做了1000次模擬計算，其計算結果如表2所示；含兩個粗差在各邊上的情況，每種情況做了1000次模擬計算，其計算結果如表3（先驗中誤差為±3mm）。

表2 僅含有一個粗差在各邊上的1000次模擬計算結果

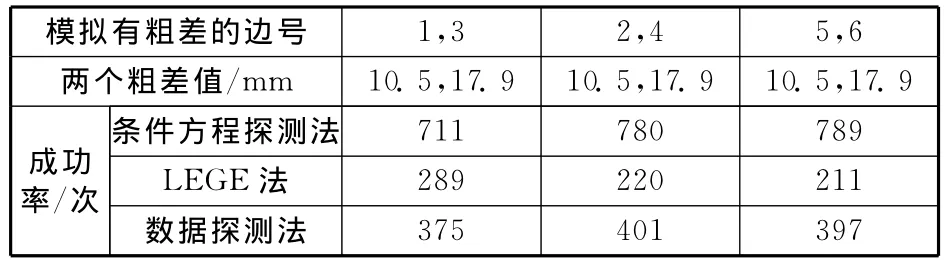
表3 含有兩個粗差在各邊上的1000次模擬計算結果

比較表2的數據得出，本文提出的方法能直接有效地找出粗差所在的觀測值，而且成功率更高。

2）此算例來源于於宗儔教授的論文[6]，一水準網，高差觀測數n＝19，必要觀測數t＝10，多余觀測數r＝n-t＝9，分別模擬1，2，3，4，5，6個粗差的情況（如圖2所示）。

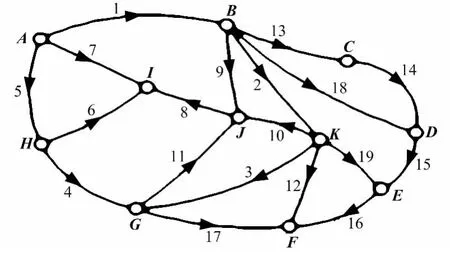
圖2 模擬6個粗差觀測結果

按上述方法自動生成的隨機誤差加入到真值，模擬出觀測值，同時用LEGE法和數據探測法進行相同模擬計算，其對比如表4所示。

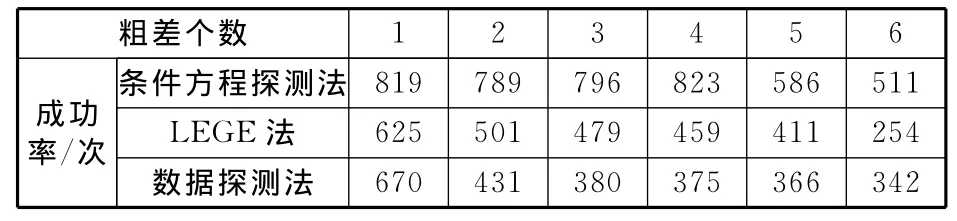
表4 增加粗差個數和高差觀測數的數據模擬計算結果

對于LEGE法，0次搜索并沒有進行，只進行最小二乘平差計算。而以后的搜索都會增加，當第k次時，共有個組合，并將組合的平差結果來修正原觀測值后再進行下一次平差計算，然后一次一次迭代、搜索。此方法原理理解比較難，實現過程比較繁瑣，效率也不太高。對比來看，本文提出的方法簡便快捷，不必進行搜索迭代計算，也不必進行每次的平差計算，大大簡化了粗差探測的步驟，而且定位效率也較高。

4 可靠性試驗

由算例1，僅對含一個粗差的情況做如下試驗。把一個粗差放在同一個位置上，用不同大小的粗差模擬出觀測值。同樣，每改變一次粗差大小，做1000次模擬測試計算，得到如表5所示的結果（先驗中誤差為±3mm）。

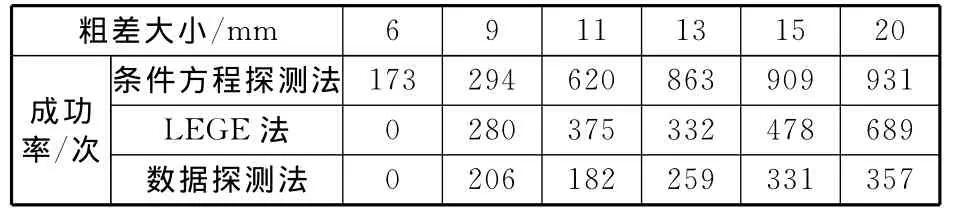
表5 用條件方程式直接探測多維粗差的方法探測最小粗差的能力

根據試驗結果顯示，隨著粗差的增大，3種方法探測粗差的能力在增加，粗差探測的成功率也在提高；在探測確定接近極限誤差附近的粗差值上，本文所提出的方法的探測能力更強。

5 結論和建議

1）因條件方程式的閉合差能真實反映出觀測值中粗差的存在，所以用條件方程式直接探測多維粗差的方法是可行的。從基本的條件方程式計算閉合差，并運用其閉合差作為粗差的判斷依據，該方法的原理簡單易懂、步驟簡便易實現、計算效率高、探測的準確性高、對粗差大小的靈敏度高。運用該方法進行計算，避免了反復進行平差和權陣計算，避免了反復多次迭代、搜索計算，完全可以一次計算，找出所有粗差項。

2）表2、表3說明了本方法能夠準確可靠地探測粗差。和其他兩方法比較說明，在相同條件下，本文提出的方法探測粗差的成功率更高。由表4證明了當觀測邊數增加時，也不會影響探測粗差的成功率，但隨著粗差個數的增加，成功率在降低；從表5中得出，隨著粗差值的增大，對這3種方法來說，成功找出粗差的幾率就更大，也說明了該方法的探測接近極限誤差附近的粗差的能力更強，其對粗差大小的靈敏度更高。

[1]歐吉坤.粗差的擬準檢定法（QUAD法）[J].測繪學報，1999，28（1）：25-20.

[2]劉根友.粗差檢定的兩種途徑[J].大地測量與地球動力學，2005，25（3）：29-33.

[3]Baarda W.Statistical Concepts in Geodesy[J].Neth Comm，1967，2（4）：74.

[4]李德仁，袁修孝.誤差處理與可靠性理論[M].2002：236-249.

[5]范東明.測量平差模型誤差的驗后檢驗[J].西南交通大學學報，2004，39（3）：349-351.

[6]於宗儔，李明峰.多維粗差的同時定位與定值[J].武漢測繪科技大學學報，1996，21（4）：323-329.

[7]劉大杰，陶本藻.實用測量數據處理方法[M].北京：測繪出版社，2000：67-71.