基于環形對稱Gabor多通道紋理加權的人臉識別

王昱蓉，白 靜，張雪英

（太原理工大學 信息工程學院，太原 030024）

人臉識別技術作為多學科領域的具有挑戰性的難題，覆蓋了數字圖像處理、模式識別、計算機視覺、心理學、數學等諸多學科的內容，同時也廣泛地應用于國家安全、軍事以及家庭生活等方面[1]。人臉識別算法的優劣，很大程度上取決于人臉的特征提取及其精準表示，良好的人臉表示可以使最簡單的分類器達到最好的識別效果。Gabor變換（Gabor Transform，GT）不僅可以獲取時間和頻率的最小不確定性，而且與人的視網膜神經細胞的接受場模型具有驚人的相似性[2]，是一種經典的人臉特征提取方法。但是目前普遍采用的GT至少存在兩方面的缺陷：

1）GT通常取5尺度，8方向的基函數，變換后的特征維數是變換前的40倍，致使系統冗余增加。

2）旋轉不變性對圖像識別非常重要，而GT的方向選擇性使其不具備旋轉不變性，在人臉圖像的平面旋轉時性能下降。

為解決上述問題，首先采用一種變形的GT，即環形對稱Gabor變換（Circularly Symmetrical Gabor Transform，CSGT）[3-5]，用于提取人臉的多通道特征，它可以有效地克服GT的上述缺陷，并對各種干擾具有一定的魯棒性。然后，為了充分利用CSGT的特性，進一步提高特征提取的準確性以及實際應用的靈活性，本文對CSGT提取的多通道特征進行了優化選擇和融合，有效地結合了紋理圖像檢索的紋理統計特征提取算法[6]和自適應加權算法[7]，提出了一種基于CSGT的人臉特征提取改進算法——CSGT多通道紋理加權（Weighted Multichannel Texture of Circularly Symmetrical Gabor，CSGT-WMT）算法，該算法充分獲取了CSGT的魯棒局部紋理特征，有效解決了識別的“誤配準問題”[8]，提取出鑒別能力強的特征，減少數據冗余。最后，采用PCA加權算法降維，使用簡單的歐氏距離得到分類識別結果，實現人臉識別。

分別在ORL，Yale和FERET人臉庫上進行實驗，相比于GT和其它傳統算法，以及CSGT和其改進算法，本文算法識別率高，數據量小，可行性高，對光照、姿態、表情、局部形變等干擾具有很好的魯棒性，且靈活適應于不同的人臉庫，具有很好的分類性能和實際應用能力。

1 環形對稱Gabor變換

傳統Gabor濾波器核函數定義如下：

將式中與方向有關的頻率向量kuv加以修改，忽略補償直流成份，得到CSGT核函數，定義為：

可見，CSGT是一個高斯函數約束的平面波。

σ決定窗口的寬度和波長的比例關系，

式中：φ為濾波器倍頻程帶寬；σ一般取2π。

對于一幅人臉圖像，經過CSGT變換，即人臉圖像I（x，y）與CSGT核函數ψv的卷積，定義為：

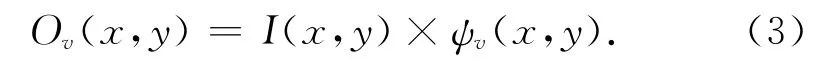
Ov（x，y）為復數，其幅值 Mv（x，y）為：

式中：Re（Ov（x，y））和Im（Ov（x，y））分別為 Ov（x，y）的實部和虛部。

因此，得到v（v＝1，2，…，5）個尺度的幅度響應Mv（x，y），因其比較穩定，通常作為人臉圖像的CSGT多尺度特征[5]，如圖1所示。

圖1 人臉圖像的CSGT多尺度特征

CSGT具有傳統GT的突顯局部紋理、多尺度分析等性質，還具有兩個重要性質：

1）冗余降低。CSGT的基函數明顯比傳統GT減小。傳統GT得到40個變換結果，而CSGT僅保留5個尺度上的變換結果，冗余量是傳統GT的1／8。

2）嚴格的旋轉不變性。旋轉不變性對圖像識別非常重要，而在實際應用中，圖像的旋轉是任意的。GT的方向選擇是離散的，使其不具備旋轉不變性。如圖2，圖3所示。對于傳統GT，圖像先變換再旋轉，與圖像先旋轉再變換，有所差別；而CSGT則不同，具有嚴格旋轉不變性。

圖2 傳統GT的旋轉敏感性測試

圖3 CSGT的旋轉不變性測試

2 基于CSGT的人臉特征提取改進算法

2.1 算法描述

人臉特征提取算法流程如圖4所示，在得到CSGT多尺度特征之后進行改進，提出了一種基于CSGT的人臉特征提取改進算法，具有兩點重要改進。

2.1.1 CSGT特征優選

CSGT變換后的幅度圖像突顯出了局部的紋理信息，但數據量是變換前圖像的5倍。因此，有必要對CSGT特征進行優選，減少冗余，提取重要的且利于識別的紋理信息。本文將紋理圖像檢索的紋理統計特征（Texture Statistical Feature，TSF）提取方法[6]與CSGT相結合，構成了算法CSGT-TSF。該算法使用統計特征提取方法，有效解決識別的“誤配準問題”；并結合子圖像的處理方式，充分獲取CSGT的魯棒局部紋理特征，減少數據冗余。由此構建了人臉圖像的CSGT多通道紋理特征。

2.1.2 自適應加權融合

在CSGT-TSF算法的基礎上，為了區分不同通道紋理統計特征的重要性，讓鑒別能力強的特征占主導地位，減少干擾因素的影響，提出了一種基于CSGT的人臉特征提取改進算法——CSGT多通道紋理加權算法。該算法采用自適應加權融合，動態調整不同通道特征的權值w（1，2，…，10），融合得到最具鑒別能力的特征，即自適應加權的CSGT紋理特征。該特征靈活適應于不同的干擾變化。

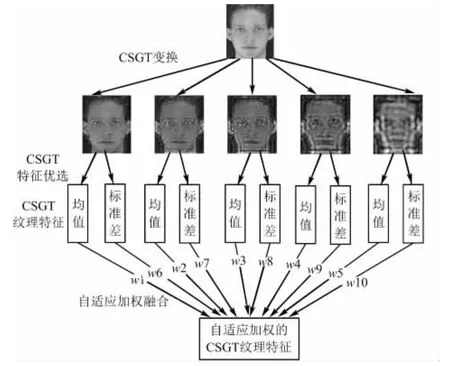
圖4 CSGT-WMT人臉特征提取算法流程示意圖

2.2 CSGT-TSF算法

CSGT-TSF算法首先將得到的人臉圖像的CSGT多尺度特征劃分子圖像，然后分別對每個子圖像進行紋理統計特征提取，最后分別在各尺度上級聯子圖像紋理統計特征提取結果。

對于人臉圖像I，在CSGT多尺度特征圖像Mv（x，y）上劃分大小相同的子圖像，假設子圖像大小為m×n，個數為K，每個子圖像Ik（k＝0，1，…K-1）的紋理統計特征均值μv，k和標準差σv，k分別為：

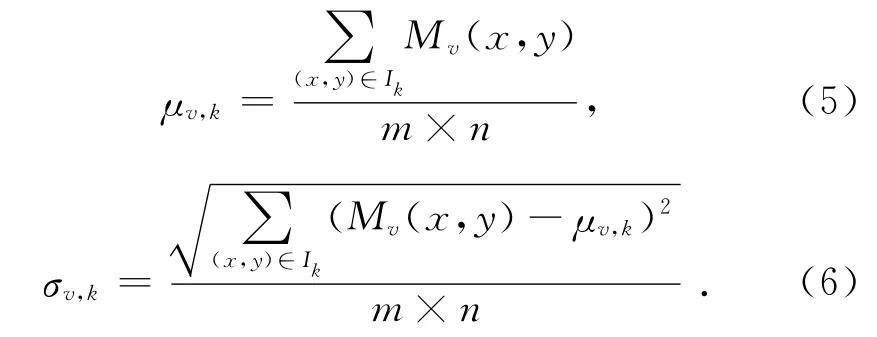
然后，在各尺度上分別級聯其子圖像的紋理統計特征均值μv，k和標準差σv，k，分別得到各尺度的均值紋理特征μv和標準差紋理特征σv，由它們構成了人臉圖像I的多通道CSGT紋理特征（CSGT Texture Features，GTF），GTF用G表示，定義為：

CSGT-TSF算法得到的統計特征GTF克服了先前點對點識別的“誤配準問題”，數據量為紋理統計前的2／（m×n）。

2.3 CSGT多通道紋理加權（CSGT-WMT）算法

人臉圖像的每一個尺度信息在人臉識別中的貢獻大小是不同的，如果直接將得到的所有尺度的紋理統計特征直接級聯勢必會造成冗余及降低識別率[9]。因此，有必要區分不同通道的紋理統計特征的重要性，然后根據重要程度進行特征的融合。

自適應加權融合算法，靈活適應于光照、姿態、表情、局部形變等干擾及人臉庫的變化，CSGTWMT算法在CSGT-TSF算法基礎上采用線性判別分析的優化思想[10]，得到訓練樣本各個通道的紋理統計特征GTF在不同類別樣本的集中和離散程度，動態調整不同通道GTF的權值大小，融合得到最具鑒別能力的特征。

首先分別計算GTF在第l（l＝1，2，…，10）通道上的類內方差和類間方差，定義為：

Gi，j，l為第i類第j樣本在第l通道上的GTF矢量。Gi，j，l（q）是特征矢量的第q個元素標量。εi，l（q）是第i類訓練樣本Gi，j，l（q）的均值，εl（q）是全部訓練樣本Gi，j，l（q）的均值。N 為訓練樣本總數，k為樣本類別數，ni為第i類樣本數。

式中：q∈｛1，2，…，d｝；d為 GTF矢量長度。

因此，得到通道l的權值wl：

于是，可以根據wl（l＝1，2，…，10）衡量每個通道的GTF的鑒別能力，進一步，將所有通道的GTF加權求和，得到自適應加權的CSGT紋理特征（A-daptive Weighted CSGT Texture Features，WGTF），WGTF用W 表示，定義為：

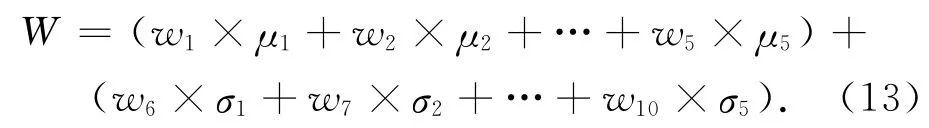
人臉樣本經過CSGT-WMT算法，進行CSGT特征優化選擇和融合得到的樣本特征WGTF，提取并融合了最具鑒別能力的特征，削弱了鑒別能力不強的特征，以及減少光照、姿態等干擾，并且數據量減少為原始樣本的1／（m×n）。

3 PCA加權降維及空間分類

為進一步降低樣本維數實現空間分類，在沒有足夠的先驗知識情況下，應該平等的看待PCA的特征向量的每一個獨立分量，每個分量應具有相同方差，因此本文采用PCA加權（Weighted PCA，WPCA）[11]，對 CSGT-WMT 得到的人臉特征 WGTF進行降維，經過WPCA，訓練和測試樣本分別得到其對應的投影向量。最后，采用簡單的歐氏距離進行分類器設計，實現最終的人臉識別。

4 實驗結果與分析

實驗分別在ORL、Yale和FERET 3個人臉庫上進行，采用5尺度CSGT，5尺度8方向GT，下采樣和TSF分塊大小均為4×4，WPCA降維方式和歐氏距離分類器。首先，在ORL人臉庫上，對降維算法PCA和WPCA進行對比，將GT＋WPCA、CSGT＋WPCA、CSGT-TSF＋WPCA 和 CSGTWMT＋WPCA進行對比實驗。然后，在Yale和FERET人臉庫上分別進行CSGT基礎上的改進實驗及其對比。

ORL人臉庫包括40組人臉樣本，每組10張，共400張。每組是一個人包括姿態、表情和面部飾物等變化圖像，大小為112×92。表1給出了每種算法分別取不同數目訓練樣本對應得到的識別率結果，在訓練樣本數為2～8時，分別隨機選取訓練樣本進行30次實驗，實驗結果取平均；訓練樣本數為9時使用排一法得到結果。表2給出了各算法在取不同數目的訓練樣本下分別使用排一法識別的CPU運行時間。從表1和表2可以看出，降維算法WPCA的識別率優于PCA，且識別時間有所減少；CSGT＋WPCA相比GT＋WPCA的平均識別率有所提高，且數據量減少，識別時間明顯降低；改進的CSGT-WMT＋WPCA算法相比CSGT＋WPCA，不僅識別率提高了，最高識別率可達到98.47%，而且數據量及運行時間也有大幅度的減少。通過實驗驗證了CSGT優于GT以及本文算法CSGT-WMT的有效性和可行性。

表1 ORL人臉庫上各種算法識別率 %

表2 ORL人臉庫各種算法識別時間 s

Yale人臉庫包括15個志愿者，每人11幅，共165幅人臉圖像，圖像大小為100×100。本文選擇每人前6張圖像作為訓練樣本，其余作為測試樣本進行實驗。實驗包括表情和光照的變化，對比了CSGT＋WPCA和其改進實驗：CSGT-TSF＋WPCA和CSGTWMT＋WPCA。實驗結果如圖5所示。

圖5 CSGT及其改進算法在Yale上的實驗比較

FERET人臉庫包括200個志愿者，每人7幅圖像，圖像大小為128×128。本文選取其中60個人的圖像，每人前4幅作為訓練樣本，其余作為測試樣本進行實驗。實驗包括豐富的表情、光照和姿態等變化，對比了CSGT和其改進算法。實驗結果如圖6所示。

圖6 CSGT及其改進算法在FERET的實驗比較

由圖5、圖6可見，CSGT-TSF識別率相比CSGT有所改進，算法CSGT-WMT識別率在CSGT-TSF基礎上有很大提高，自適應加權融合了最具鑒別能力的人臉特征，使之能降低不同干擾（光照，姿態，表情）對其影響，其識別率在FERET人臉庫干擾增多的情況下與Yale人臉庫中的相比減小幅度不大，因此可以靈活適用于不同的人臉庫，具有很好的實際應用能力。

5 結論

提出的CSGT-WMT算法，識別率高，對光照、姿態、表情等影響具有很好的魯棒性，靈活適應于不同的人臉庫，并且數據量小識別時間短可行性強，相比CSGT和GT等方法具有明顯的優勢，具有很高的實用價值。但隨著不同人臉庫干擾因素的增多，影響了識別率，因此有必要進一步對各種干擾因素進行綜合分析深入研究，使用復雜的分類器進一步提高識別效果。

[1]張翠平，蘇光大.人臉識別技術綜述[J].中國圖象圖形學報，2000，5（11）：885.

[2]張國云，郭龍源，吳健輝，胡文靜.計算機視覺與圖像識別[M].北京：科學出版社，2012.

[3]Zhu Zhenfeng，Tang Ming，Lu Hanqing.A New Robust Circular Gabor Based Object Matching by Using Weighted Hausdorff Distance[J].Pattern Recognition Letters，2004，25（4）：515-523.

[4]Wang Huiyuan.Face Recognition Approaches Based on Linear Subspace and Circularly Symmetrical Gabor Transforms[D].Jinan，China：School of Information Science and Engineering，Shandong University，2007（in Chinese）.

[5]王進軍，王匯源，吳曉娟.基于環形對稱Gabor變換和PCA加權的人臉識別算法[J].模式識別與人工智能，2009，22（4）：635-638.

[6]Manjunath B S，Ma W Y.Texture features for browsing and retrieval of image date[J].IEEE Trans.on PAMI，1996，18（8）：837-842.

[7]楊青山，郭成安，金明錄.基于Gabor多通道加權優化與系數表征的人臉識別方法[J].電子與信息學報，2011，33（7）：1620-1621.

[8]余磊，何中市.Gabor小波變換在人臉識別中的應用研究[D].重慶大學計算機學院，2009.

[9]Amin M A，Yan H.An empirical study on the characteristics of Gabor representations for face recognition[J].International Journal of Pattern Recognition and Artificial Intelligence，2009，23（3）：401-431.

[10]李文輝，高璐，林逸峰.特征選擇模糊加權多通道Gabor人臉識別[J].湖南大學學報（自然科學版），2013，40（4）：87-93.

[11]Wang Huiyuan，Wu Xiaojuan.Weighted PCA Space and Its Application in Face Recognition[C]／／Proc of the 5thInternational Conference on Machine Learning and Cybernetics，Guangzhou，China，2005，Ⅶ：4522-4527.