例談多物體周期性運動時間與空間的統一
王松濤
(中山市華僑中學,廣東 中山 528400)
多物體周期性運動的問題是高中物理中最為復雜的內容之一,由于同時運動的物體多、過程多,許多學生在分析時往往顧此失彼,不知所措.而從功和能的角度去分析就更加霧里看花,難辨是非了.
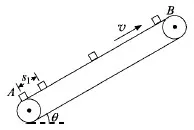
圖1
例題.一傳送帶裝置如圖1所示,傳送帶在AB區域是傾斜的,傾角θ=30°.工作時傳送帶向上運行的速度保持v=2m/s不變.現將質量均為m=2kg的小貨箱(可視為質點)一個一個在A處放到傳送帶上,放置小貨箱的時間間隔均為T=1s,放置時初速度為零,小貨箱一到達B處立即被取走.已知小貨箱剛放在A處時,前方相鄰的小貨箱還處于勻加速運動階段,此時兩者相距為s1=0.5m.傳送帶裝置由電動機帶動,傳送帶與輪子間無相對滑動,不計輪軸處的摩擦,取g=10m/s2.除了剛釋放貨箱的時刻,若其他時間內總有4個貨箱在傳送帶上運動,求每運送一個小貨箱電動機對外所做的功,并求電動機的平均輸出功率P.
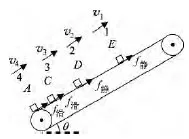
圖2
解法1:小貨箱剛放在A處時,前方相鄰的小貨箱已經運動了時間T.如圖1有代入數據解得加速度大小a=1m/s2.傳送帶上總共有4個貨箱在運動,說明貨箱1在A處釋放后經過t=4T的時間運動至B處.此時,第5個貨箱恰要放入A處,如圖3,圖2為T=1s前的情景.
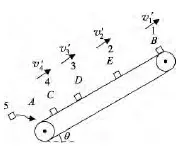
圖3
貨箱在位置D處速度與傳送帶速度相等,此刻,貨箱所受滑動摩擦力突變為靜摩擦力,貨箱在此后的時間內隨傳送帶做勻速運動,f靜=mgsinθ.傳送帶克服該貨箱的靜摩擦力做的功為W2=f靜v(t-t1),代入數據解得W2=40J.
每運送一個小貨箱電動機對外做的功為W=W1+W2=88J.
放置小貨箱的時間間隔為T,則每隔時間T就有一個小貨箱到達B處,因此電動機的平均輸出功率為88W.
對于解法1,很多學生感到迷惑.貨箱1從A處運動到B處的4s時間內,電動機不是同時在對貨箱2、3、4做功嗎?為什么解答中只計算了電動機對貨箱1做的功,而并未計算對貨箱2、3、4做的功呢?另外,運送一個貨箱的時間明明是4s,即電動機對一個貨箱做功的時間為4s,為什么計算電動機輸出功率時這個時間卻又取1s呢?
分析:首先,運送一個貨箱對應的時間是1s而非4s.因為觀察者在B處每隔1s就可取得1個貨箱,這與該貨箱是何時放上去的并無關系.其次,電動機對貨箱1做功的同時,很明顯對貨箱2、3、4也做了功.題目中要求每運送一個小貨箱的過程中電動機對外所做的功,顯然,更直接地看應是求在1s的時間內,電動機對貨箱1、2、3、4所做的總功.那么,為何答案中卻是求電動機對一個貨箱在4s內所做的功呢?
現在,我們來分析4個貨箱同時做周期性運動的特點.貨箱1在4個連續的1s內的運動分別經歷了A→C、C→D、D→E和E→B等4個過程,而貨箱1、2、3、4在1s內的運動為貨箱4經歷了A→C,貨箱3經歷了C→D,貨箱2經歷了D→E,和貨箱1經歷了E→B的4個過程.即貨箱1在4s內的運動恰好是經歷了貨箱1、2、3、4在1s內所經歷的過程.故電動機對貨箱1在連續4s內所做的功應等于電動機在1s內對連續4個貨箱所做的功.因此用電動機在1s內對4個貨箱所做的功來驗證.
解法2:在從圖2到圖3的1s內,貨箱1和2受靜摩擦力作用,而貨箱3和4受滑動摩擦力作用.電動機克服4個貨箱的摩擦力做功為W=(2f滑+2f靜)vT=88J.
結論:解法1和解法2的一致性正好說明了多物體周期性運動時間和空間的統一.
以上從摩擦力做功的角度驗證了多物體周期性運動時間和空間的統一,還可以變換角度,從功是能量轉化的量度出發,用能量轉化這個更本質的視角來探討這一問題.
貨箱放到傳送帶上,電動機多做的功對應于多消耗的電能,而電動機多消耗的電能使得貨箱的機械能增加,同時,貨箱與傳送帶摩擦產生了內能.
解法3:從圖2到圖3的一個T內,電動機對外做的功等于1、2、3、4共4只貨箱動能的增加、重力勢能的增加和貨箱3、4與傳送帶之間滑動摩擦產生內能的總和.
系統增加的動能為ΔEk=Ek′-Ek.
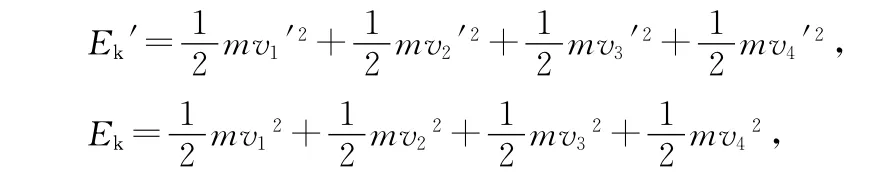
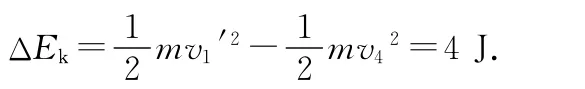
系統增加的重力勢能為ΔEp=Ep′-Ep.
Ep′=mg·AC·sinθ+mg·AD·sinθ+mg·AE·sinθ+mg·AB·sinθ,
Ep=mg·AC·sinθ+mg·AD·sinθ+mg·AE·sinθ.故ΔEp=mg·AB·sinθ=mg(·2T+v·2T )sinθ=60J.
由圖2到圖3的一個T內,貨箱1和2勻速運動,不會摩擦生熱.
貨箱3與傳送帶相對滑動的路程為
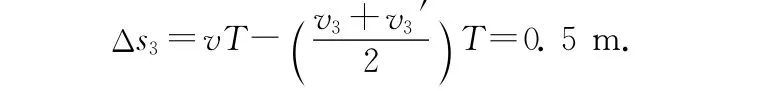
貨箱4與傳送帶相對滑動的路程為
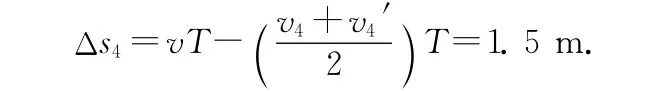
故ΔE內=f滑·Δs3+f滑·Δs4=24J.
圖2到圖3的一個T內,4個貨箱和傳送帶總的能量變化為ΔE=ΔEk+ΔEp+ΔE內=88J.故電動機對外做功為88J.
那么一只貨箱在從A處運動到B處的4s時間內,能量變化又如何呢?
解法4:一只貨箱在從A處運動到B處過程中其能量變化為
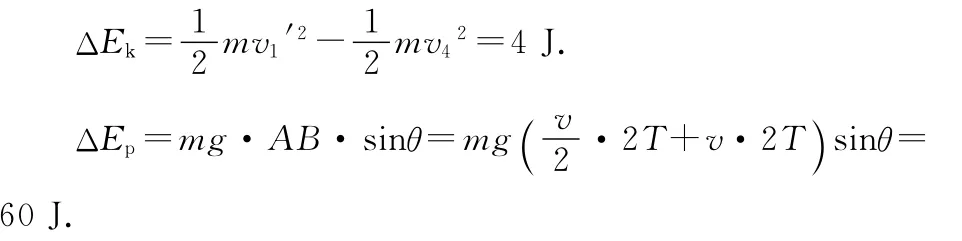
貨箱在前2s內相對于傳送帶滑動的路程為
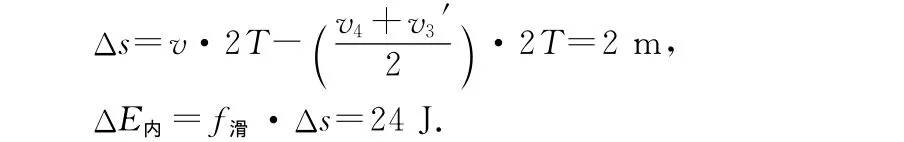
可得ΔE=ΔEk+ΔEp+ΔE內=88J.故電動機對外做功為88J.
從能量轉化的角度我們再次驗證了多物體周期性運動時間與空間的統一性.
結論:多物體周期性運動具有物體多、過程多等復雜性,但卻具有空間與時間周期性統一的規律.以上4種解法都體現了這一特點,如果能很好地利用這一點,就能化繁為簡,舉重若輕.例如本題中解法2和解法4相對于解法1和解法3就更為簡單明了.

