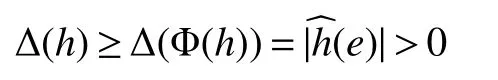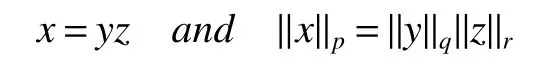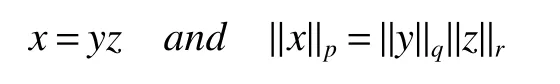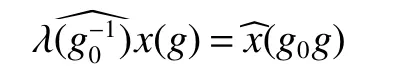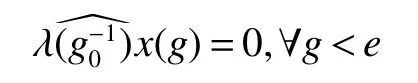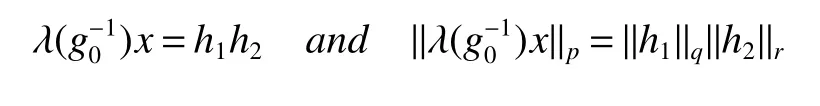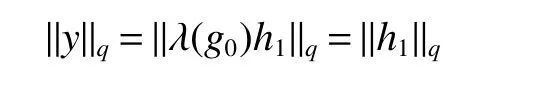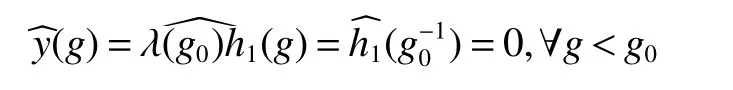Group von Neumann Algebra?
Ahmetniyaz Ahmetjan,Turdebek N Bekjan
(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)
Abstract: Let G be a discrete group with a left regular representation λ,VN(G)is a group von Neumann algebra generated by λ(g).We characterize the Hardy space on the group von Neumann Algebra.
Key words:group von Neumann algebra,Fourier series,Hardy space,outer operators
0 Introduction
LetGis a discrete group,l2(G)is a Hilbert space.Let(δg)g∈Gbe the canonical basis ofl2(G),i.e.,δgis the function on G that takes value 1 atgand zero elsewhere.Let λ :G→B(l2(G))be the left regular representation.Namely,for anyg∈G,λ(g)is the unitary operator onl2(G)de fined by
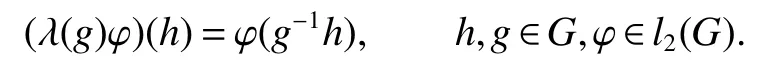
Note that λ(g)δh=δghfor allg,h∈G.The reducedC??algebra(G)and the group von Neumann algebraVN(G)ofGare respectively theC??subalgebra and von Neumann subalgebra ofB(l2(G))generated by{λ(g):g∈G}.Let C(G)be the family of all finite sums Σα(g)λ(g)with α(g)∈C.Then it’s norm closure and w*-closure are(G)andVN(G)respectively.
Givenx∈VN(G),we consider the vector state τG(x)=<δe,xδe>whereedenotes the identity element ofG.Thus τ is a faithful normal tracial state onVN(G).
Thus(VN(G),τG)is noncommutative probability space,we called noncommutative group von Neumann Algebra.LetLp(VN(G),τG)denoted theLpspace over the noncommutative measure space(VN(G),τG)-so called noncommutativeLpspace.
In general for anyx∈Lp(VN(G,τG)(forp≥1)has a Fourier series
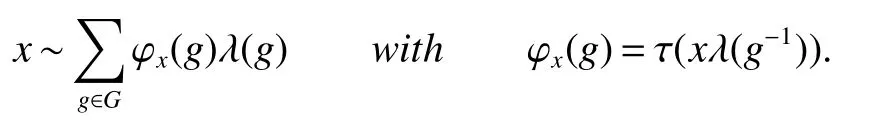
In the section 3 we consider the convergence of this Fourier series and properties of the Fourier coefficients.
In the section 4 we characterize the specific form of the Hardy space on the group von Neumann Algebra mentioned above.To this end we recall de finition of the finite subdiagonal algebra in Arveson’s[1]sense.LetMbe a finite von Neumann algebra equipped with a normal faithful tracial state τ.
De finition 1LetDbe a von Neumann subalgebra of M,and let Φ :M→Dbe the unique normal faithful conditional expectation such that τ?Φ=τ.A finite subdiagonal algebra ofMsatisfying following conditions
(i)A+A?is w*-dense inM;
(ii)Φ is multiplicative onA,i.e.,Φ(ab)=Φ(a)Φ(b)for alla,b∈A;
(iii)ATA?=D.whereA?is the family of the adjoints of the elements ofA,i.e.,A?={a?:a∈A}.
The algebraDis called thediagonalofA.It’s proved by Exel[2]that a finite subdiagonal algebraAis automatically maximal.This maximality yields the following useful characterization ofA

whereA0=ATkerΦ(see[1]).We will use the following notation:IfSis a subset ofLp(M),[S]pwill denote the closure ofSinLp(M)(with respect to thetopology in the case ofp=∞).Forp<∞we de fineHp(A)to be the closure ofAinLp(M).ThusHp(A)=[A]p.Formula(1)admits the followingHp(A)analogue proved by Saito[3]
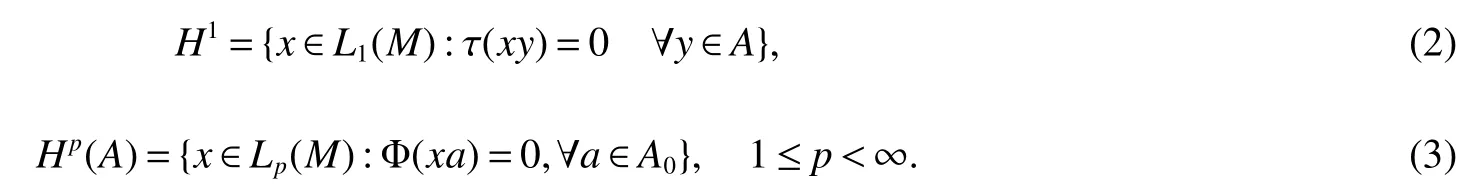
Starting with the Arveson’s pioneer work these noncommutative Hardy spaces have received a lot of attention,Most results on the classical hardy spaces on the torus have been established in this noncommutative settings,and achieved outstanding progress on it(see[4~7]for some recent works).In this paper we give the specific form of the Hardy space on the group von Neumann Algebra.The last section contains some results in outer operators on this hardy space.We improved the Riesz type factorization(Theorem 3).
1 Preliminaries
Previous section we give de finition of C(G),VN(G)andLp(VN(G))there is some elementary results about those spaces.Besides some other conclusions will be used in section 3 and 4.
Theorem 1Let 1 ≤p< ∞,and let C(G)be the family of all finite sumsPα(g)λ(g)with α(g)∈ C,then C(G)dense inLp(VN(G)),wherep≥1.
ProofSince C(G)?Lp(VN(G)),we get[C(G)]p?Lp(VN(G)).
If[C(G)]p,Lp(VN(G))then?x0∈Lp(VN(G)),butx0 We will describeVN(G)as the left convolution algebra ofl2(G).Recall that for every ?,ψ ∈l2(G),their convolution is de fined by ??ψ is a bounded function onG.In general,it does not belongs tol2(G).Letx∈VN(G)and let ?=xδe,the symbol ofx,then ?∈l2(G)andxψ=??ψ(see[8]157). Proposition 1x∈VN(G)i ffthere exists ?∈l2(G)such thatxψ=??ψ for every ψ∈l2(G). Proposition 1 allowed us to identify an operatorx∈VN(G)with it’s symbolxδeinl2(G),then this identi fication extends to a unitary operator fromL2(VN(G))tol2(G).This allows us to de fine the symbol of anyx∈L2(VN(G)).In general for anyp≥1 we can de fine the symbol ofx∈Lp(VN(G))as the function ?xonGgiven by Then ?xis a bounded function on G(majorized by kxkp). Indeed,|?x(g)|=|τ(xλ(g?1))|≤kxkpkλ(g?1)kq=kxkp?g∈G,then Therefore,we can symbolically write The sum on the right is the Fourier series ofxin the basis{δg}g∈G.Same as the classical case[9]we denote the Fourier coefficients withg),i.e.,g)=?x(g). Proposition 2We keep the notations above,Fourier coefficients have the following properties ProofThe proof of the(i),(ii),(iv),(v),(vi)is obvious.We only sketch the proof of(iii)and(vii).Since We get(iii). (vii)(1)putx=λ(g),y=λ(h)then (3)In generalx∈Lp(VN(G)),y∈Lq(VN(G)),thenxy∈Lr(VN(G))∞),then From now on(G,≤)will be a countable totally ordered discrete group(order (i)Thepartial sum (ii)Thesquare Fej′er mean Proposition 3The following are valid forx∈L2(VN(G)) (i)(Plancherel’s identity) (ii)The operator x is equal to theL2(VN(G))limit of the sequence (iii)The mapx→ {bx(g)}g∈Gis an isometry fromL2(VN(G))ontol2(G). Proof (ii)Sincex?SN(x)⊥SN(x), We compute that ThereforeSN(x)is a Cauchy sequence,henceSN(x)→y.On the other hand It follows that τ((x?y)λ(g?1))=0,?g∈G,which implies that τ((x?y)λ(g))=0,?g∈G.Thusx=y. (iii)LetT(?x(g)λ(g))=(?x(g))g∈GthenTis a liner map and injective isometry.It remains to show that it is surjective. Indeed,given a sequence(?x(g))g∈G∈l2(G),g∈G|?x(g))|2< ∞. Let ?x(gn),0 forn=1,2,3....,and ?x(g))=0 forg,gn,and xnsupposen>mthen From(ii)Txn→Tx(n→∞).Since ThereforeTxn→(?x(g))g∈GSoTx→(?x(g))g∈G. Lemma 1LetFN(x)is a square Fej′er mean then for everyxinL2(VN(G))we have Proof First consider the case thatx∈C(G)i.e., Therefore In general,note thatFNis a bounded liner operator.Indeed Forx∈Lp(VN(G))there existsxn∈C(G)such that Theorem 2Letx∈L2(VN(G))then the square Fej′er meanFN(x)is converges to x. ProofLetx∈L2(VN(G))then every ε>0,there existsxε∈C(G),such that And kxε?FN(xε)k2→0,(N→∞)i.e.,there existsN0,for everyN>N0 and from Lemma 1 we get following for everyN>N0, i.e.,the square Fej′er meanFN(x)is converges to x. In this section we following the method which was mentioned in Introduction,give specific form of the Hardy space on the group von Neumann Algebra and some ordinary results on this space. LetVN(G)is group von Neumann Algebra with a faithful normal tracial state τG.D={λ·1:λ ∈ C}be von Neumann subalgebra ofVN(G)and let Φ(x)= τ(x)1 which unique normal conditional expectation fromVN(G)toD.then satisfying the following(see[1]) (ii)Φ(ab)=Φ(a)Φ(b),?a,b∈A. (iii)ATA?={λ·1:λ∈C}=D. Therefore by the De finition 1Ais finite subdiagonal algebra ofVN(G)with respect to Φ,and automatically maximal.We characterize theHp(A)by the formula(1)and(2).First we have following easy checking results. Lemma 2Let(G,≤)is a countable ordered discrete group,Ais finite subdiagonal algebra ofVN(G)with respect to Φ mentioned above,then (i)A0= (ii)H1={x|x∈L1(VN(G)):?x(g)=0,?g Proof(i)For everyx∈A,i.e. (ii)H1={x∈L1(VN(G)):τ(xy)=0 ?y∈A}. Letx∈H1,ifg Ify∈A0then there exists Thusx∈H1,i.e.,H1?{x|x∈L1(VN(G)):?x(g)=0,?g By the formula(3)and Lemma 2,we immediately have the following proposition. Proposition 4Let(G,≤)is a countable ordered discrete group,VN(G)is a group von Neumann algebra.Then Hardy space on this algebra have a following form for 1 This section we consider outer operators.All results are due to Blecher and Labuschagne[10]in the case of indices not less than one,and later completeness of casep<1 in[4]by Bekjan-Xu. We starting with the following de finition of outer operators. De finition 2Let 0 Following results bases on the Hardy space on the group von Neumann algebra mentioned in previous section. Proposition 5Let 0 (i)his left outer (ii)his right outer (iii)his bilaterally outer (iv)?(Φ(h))=?(h) ProofSinceis equivalent to ?(h)=?(Φ(h))>0.Moreover A is antisymmetry(i.e.,dimD=1),therefore by the corollary 4.6 in[4]proof is clear. Proposition 6Let 0 ProofBy the Arverson-Labuschagne’s Jensen inequality(cf.[1],[4],[10]), Whence the assertion because of the Corollary 4.9 in[4]. Proposition 7Let 0 ProofThis proof is similar to that of Proposition 6.An immediate consequence of Corollary 4.12 in[4]. Theorem 3Let 0 ProofIfthen by the Proposition 7 result is holds.If=0 then there existg0∈Gsuch thatFrom Proposition 2(iv)we get Since ifg Thereforex=λ(g0)h1h2,lety=λ(g0)h1,z=h2then and Since ifg Remark 1In the paper[4]give the Riesz type factorization on the noncommutative Hardy space under condition?(x)>0.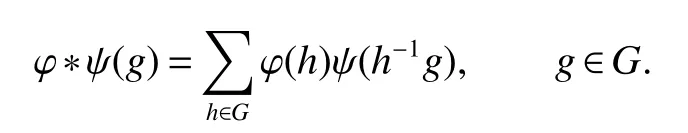
2 Group von Neumann Algebra’s Fourier Theory
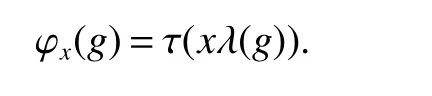
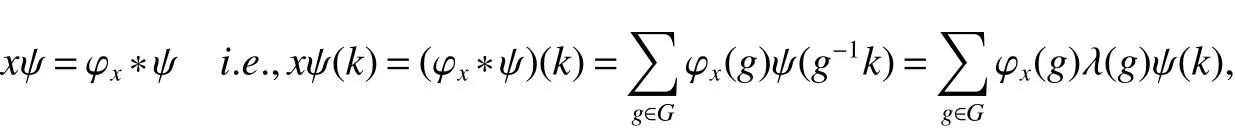
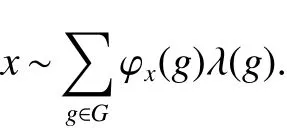
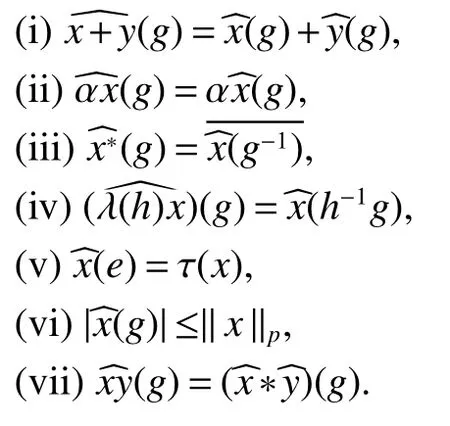
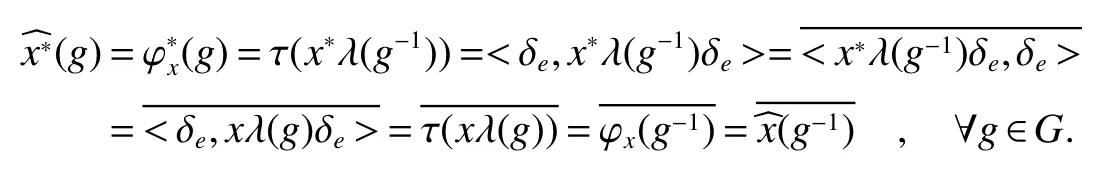
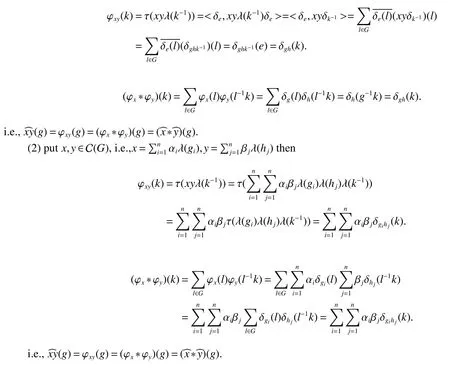
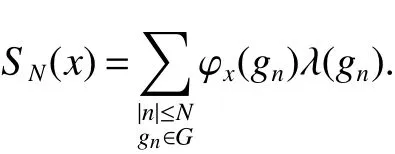
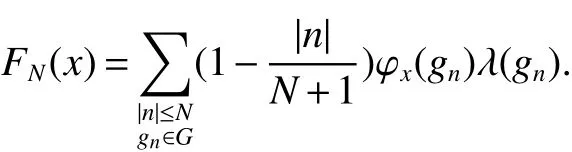
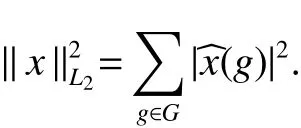
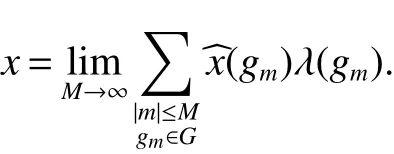
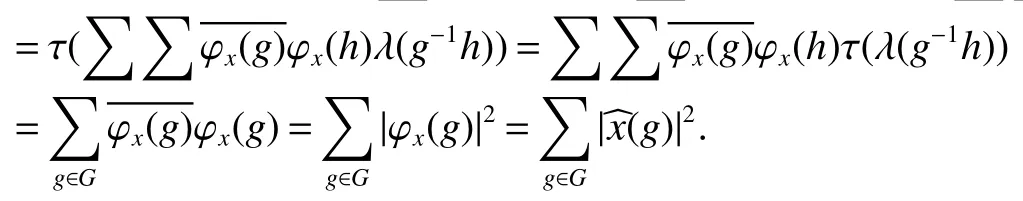
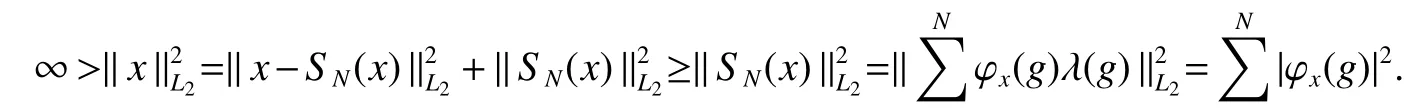
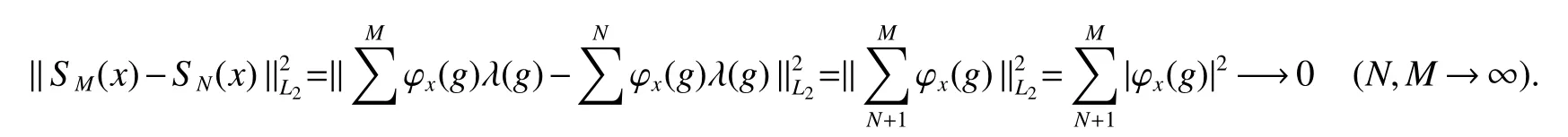
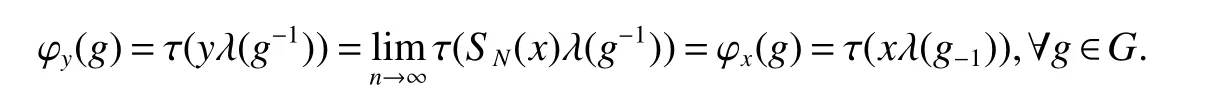
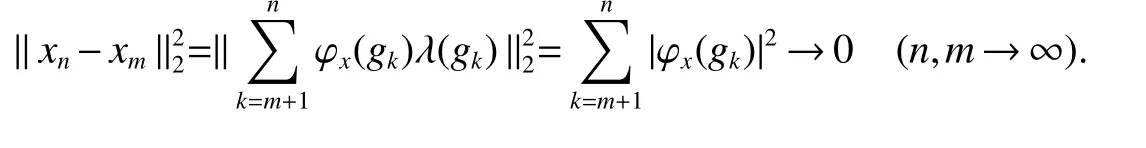
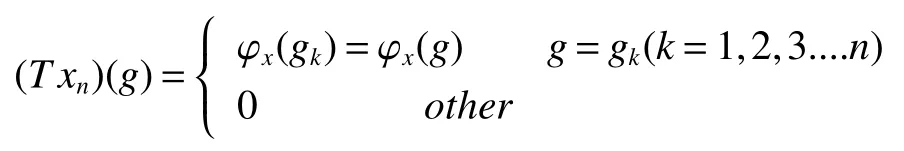
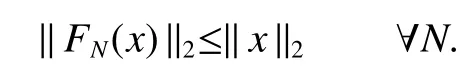
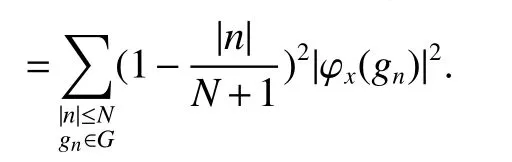
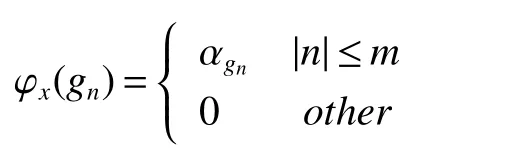
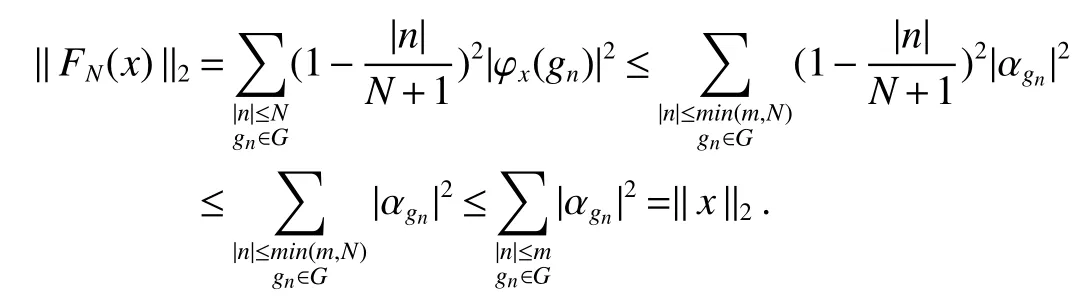
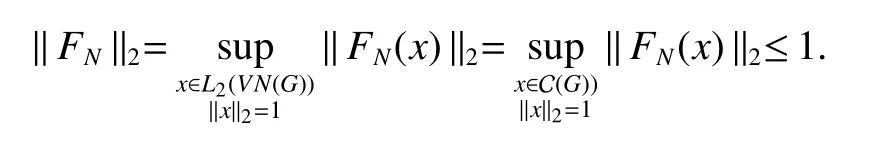
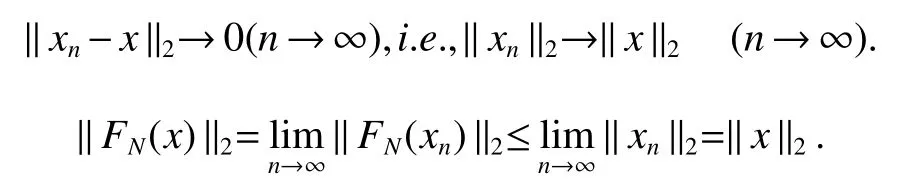
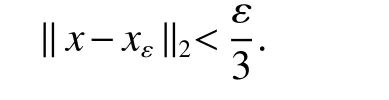
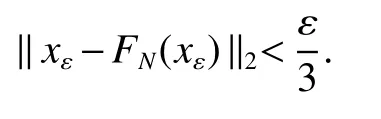
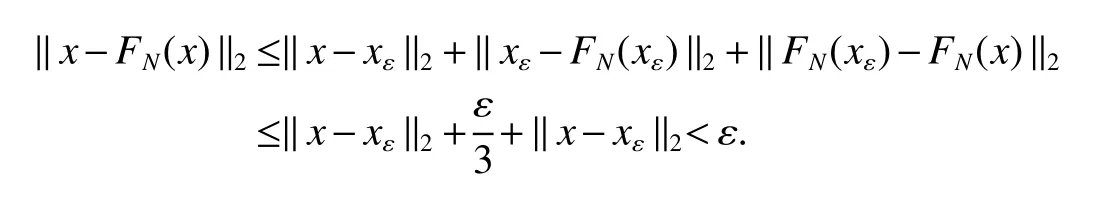
3 Group von Neumann Algebraic HPTheory
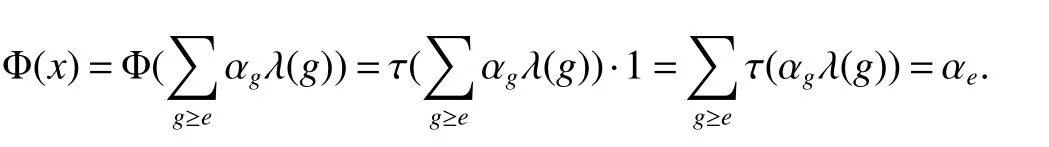
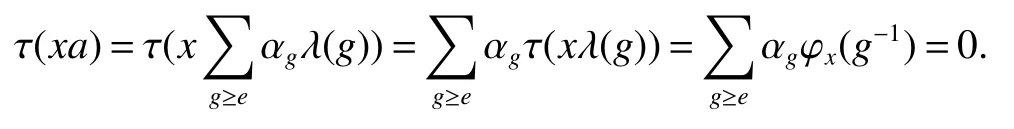

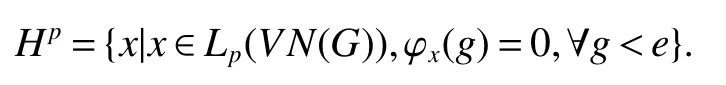
4 Outer Operators