旋翼微多普勒特性實驗分析

王 英 彭堯坤 劉飛亮 黃沛霖 姬金祖

(北京航空航天大學 航空科學與工程學院，北京100191)

當直升機處于懸停狀態時，機身及其他非旋轉部件的回波常淹沒在地海雜波中，而以較高速度旋轉的主旋翼因槳葉的旋轉作用產生的回波將成為目標探測和識別的主要特征[1－2].目標或目標的組成部分的振動或轉動會對雷達回波的頻譜產生調制，這種現象被稱為微多普勒效應(micro-Doppler effect)，并建立了不同微動形式下的數學模型[3－4].直升機主旋翼的轉動也是一種微動，它會對直升機的雷達回波頻譜產生調制，得到的旋翼微多普勒特征反過來又能夠反映目標的電磁特性、幾何結構和運動特征，從而為直升機的分類識別提供新的途徑.

為分析直升機旋翼及其組成部件的微多普勒效應特點，本文首先提出了在微波暗室測試單站微多普勒效應的測試方法，并采用該方法分別對多個直升機旋翼的不同槳葉數目情況下的微多普勒效應進行了實驗測試;在此基礎上，結合直升機可識別特征，采用短時傅里葉變換STFT(Short Fast Fourier Transform)方法對測試數據進行分析[5]，并提取出相應的微多普勒效應，研究了直升機懸停狀態下的旋翼微多普勒特性，從實驗和理論分析出發提出了影響微多普勒特征的多個關鍵因素并進行了詳細分析.

為驗證微多普勒測試方法的正確性，首先研究了不同轉速、片數旋翼微多普勒特性及旋翼微多普勒特性的頻率、極化特性.實驗表明，微多普勒的頻率和極化影響各部件的成像分辨率，而對旋翼的特征參數估算影響不大;研究了微多普勒特性的寬頻帶特性，本身已有的相位調制引起了微多普勒特性的正負頻率不對稱，研究表明通過曲線斜率仍可估算旋翼的特征尺寸.

1 實驗測試方法及數據處理

1.1 旋翼微多普勒特征和不模糊采樣率

旋翼旋轉導致的回波信號的時變多普勒頻移，即為旋翼的微多普勒效應，根據單個槳葉的微多普勒回波公式[6－7]:

式中，L為槳葉長度;λ為入射波對應的波長;ω為槳葉旋轉角頻率，rad/s;β為槳盤與入射波的夾角;N為槳葉片數;k=0，1，…，N－1，為單片槳葉編號.

由式(1)，可以得到主旋翼的微多普勒具有以下幾個特點[5，8]:①旋翼總的回波微多普勒由N個相位等間隔的正弦曲線組成，其間隔為2kπ/N，在得到旋翼微多普勒的時頻圖后，根據圖中正弦曲線的條數，即可確定出旋翼葉片的數目;②微多普勒的幅度與葉片的長度和入射角的余弦值成正比，當這些影響因素發生變化時，微多普勒的峰值和峰谷會發生變化，但對其頻率沒有影響;③微多普勒的頻率直接由旋轉角速度決定.

最大微多普勒頻率由式(2)決定[9－12]:

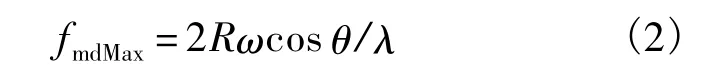
式中，R為槳尖到軸心的距離;ω=2πn/60，n為槳葉轉速;θ為入射方向與槳葉平面的夾角，本實驗為 0°.

1.2 實驗模型及實驗方法

采用兩種不同尺寸的碳纖維槳葉作為測試模型:槳葉a和b，同時制作了金屬槳轂和連接桿，可連接2，3和4片槳葉.槳葉a的槳尖到軸心的距離為0.49m，槳葉 b槳尖到軸心的距離為0.65m，連接桿前端到軸心的距離為0.18m.在微波暗室進行測試，實驗設備為安捷倫公司的矢量網絡分析儀PNA8363B，暗室測試和旋翼實物圖見圖1.

圖1 暗室測試和旋翼實物圖

安裝好旋翼測試模型后，首先設置對應的入射波頻率、極化方式和旋翼轉速.測試頻率方式包含單頻、寬頻帶信號;極化方式分為水平極化和垂直極化;通過調節直流電壓調節旋翼轉速.其次設置采樣點數和采樣頻率，采樣點數越多，STFT處理后的成像分辨率越高，處理時間越長.在滿足Nyquist采樣定律前提下通過設置中頻帶寬設置采樣頻率.最后待旋翼轉速穩定后，開始回波特性測試，需要說明的是，與 RCS(Radar Cross Section)測試不同，無需進行周向旋轉，在測試前也無需進行定標和背景測試，對測量取得的數據進行進一步處理，得到微多普勒相關特性.

1.3 數據處理方法

旋翼的微多普勒頻率是隨時間的變化而變化的，傳統的傅里葉變換缺乏局部時間信息，不能提供復雜的時變頻率調制信息，因此需要使用高分辨的聯合時頻分析方法.常見的時頻變換有短時傅里葉變換、小波分析、Gabor變換、Wigner-Vill分布、偽Wigner-Vill分布、平滑偽Wigner-Vill分布等[10].各種變換手段在使用時各有利弊，短時傅里葉變換能夠很好地區分多分量信號，不會產生交叉干擾項，且相關的算法研究比較成熟，因此本文對主旋翼回波信號進行短時傅里葉變換提取微多普勒特征[13－15]:

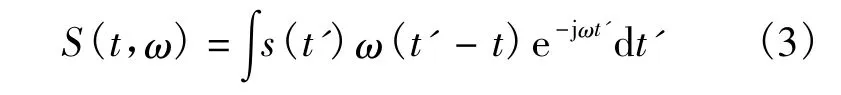
式中ω(t)為短時傅里葉變換的窗函數，這里采用高斯窗函數.通過STFT變換后，可以得到時頻變換圖，顏色深淺反映了目標回波能量的大小，通過在圖上提取正弦曲線的條數和周期，可以求出旋翼的旋轉周期和槳葉片數，然后通過提取幅值及旋翼最大微多普勒頻率，可以通過式(4)估算最小的旋翼半徑.

2 實驗方法驗證

為驗證提出實驗方法的正確性，對槳葉a旋翼進行實驗測試，測試頻率10GHz，采用水平極化，測試點數3201個，其余變化的測試參數見表1.

表1 不同的參數設置(槳葉a)

對測試結果進行STFT變換，得到微多普勒時頻曲線見圖2、圖3，可估算出的參數見表2.

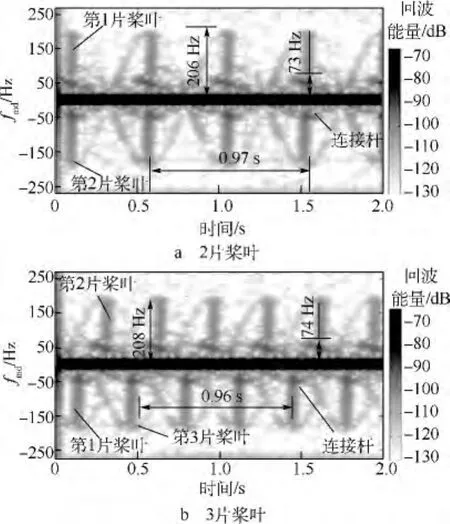
圖2 測試組號為1參數設置

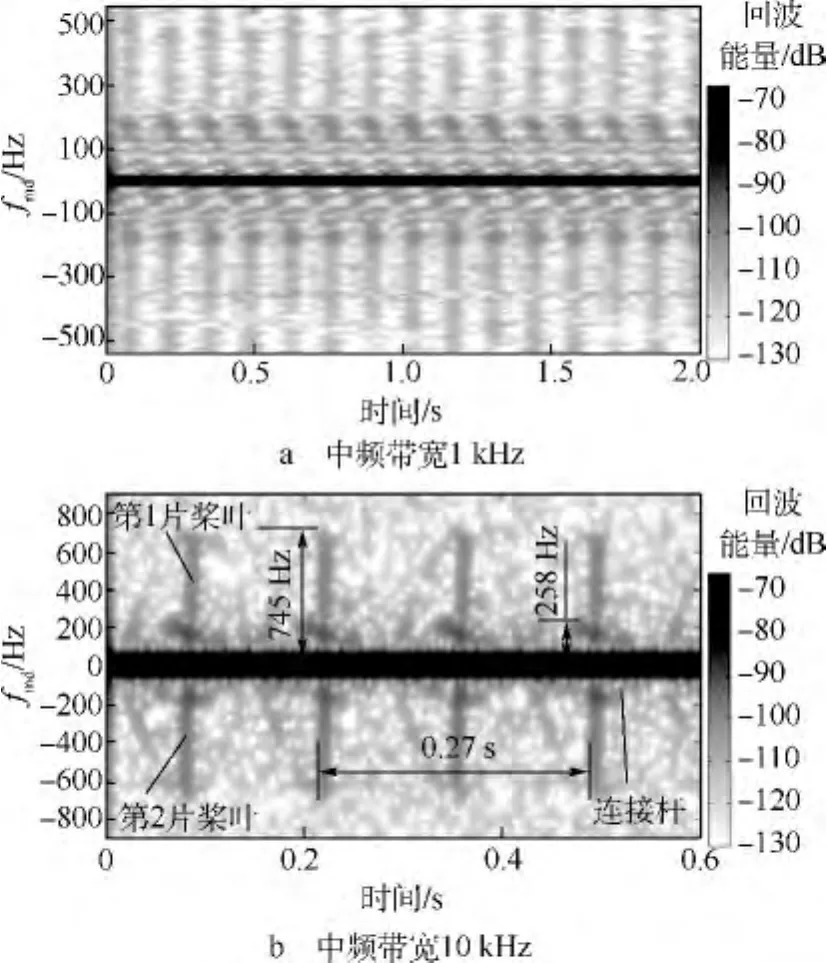
圖3 測試組號為2的參數設置

表2 估算出來的參數(槳葉a)

由表2中的數據可以看出，通過測試后估算的數據和旋翼真實的參數相比，旋翼的轉速大約為1r/s，周期為1s，測試的結果為0.97，0.96s;真實旋翼翼尖到槳轂中心的距離是0.49 m，而1a，1b和2b估算出的結果在0.48 m左右;連接桿真實距離為0.18 m，三者的估算距離在0.17 m左右.可見測試估算和旋翼真實的參數基本一致.在時頻分析中，旋轉周期是在時頻曲線上直接測量的量，所以旋轉周期誤差主要來源為時頻曲線成像分辨率帶來的測量誤差.時頻曲線成像分辨率越低，成像越模糊，旋轉周期測量誤差越大.最小長度是通過式(4)計算出來的，式中最大微多普勒頻率是在時頻曲線上測量的量，槳葉角頻率是和旋轉周期成反比的相關量.估算槳葉長度和實際結果的誤差主要有兩部分:曲線成像分辨率帶來的測量誤差，分辨率越低，長度誤差越大;旋轉周期誤差，長度誤差與旋轉周期誤差成正比.

由圖3a可知，采樣頻率不滿足Nyquist采樣定律，分辨不出旋翼的片數和旋轉周期，不能估算出所需要的參數.通過改變PNA的中頻帶寬來增加采樣率，圖3b是中頻帶寬為10 kHz的時頻圖，估算參數如上分析與真實值一致.從而驗證了實驗測試方法的正確性，同時也說明旋翼的片數和轉速不影響微多普勒特性估算.

微多普勒特性是通過沿雷達照射方向速度不同，從而帶來各個散射源微多普勒頻率不同，把各個部分散射源分開來.由圖2a、圖2b顏色的深淺代表回波能量的大小.由此可以看出，中間的橫條為電機和槳轂回波，相對能量最大，連接桿處比旋翼回波能量大.要想減縮RCS，首先得減縮電機和槳轂的散射.

3 微多普勒的頻率和極化特性

下面研究微多普勒的頻率特性和極化特性，實驗模型為槳葉b模型旋翼，轉速一定，控制在1.8 r/s，中頻帶寬選擇1 kHz，其余參數見表3.

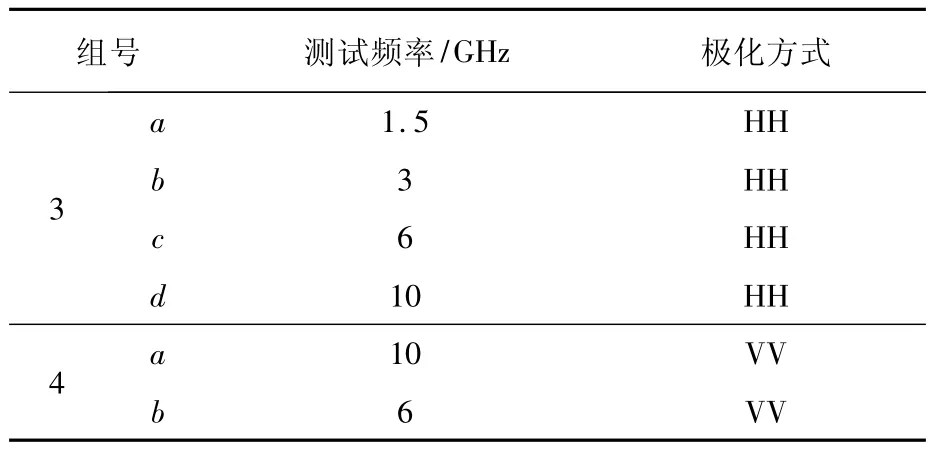
表3 不同的參數設置(槳葉b)

對測試結果進行STFT變換，得到微多普勒時頻曲線見圖4、圖5，可以估算出的參數見表4.

由表4中估算得來的參數與實際參數相比，估算旋轉周期為0.57 s左右，即大約在1.75 r/s左右，與實驗設置參數(1.75 r/s)相同.槳尖到中心點的距離是0.65 m左右，結果表明旋翼的微多普勒特性不會隨著雷達的頻率和極化特性改變，即旋翼的微多普勒特性與旋翼本身運動特性相關，可作為旋翼識別的一種手段.

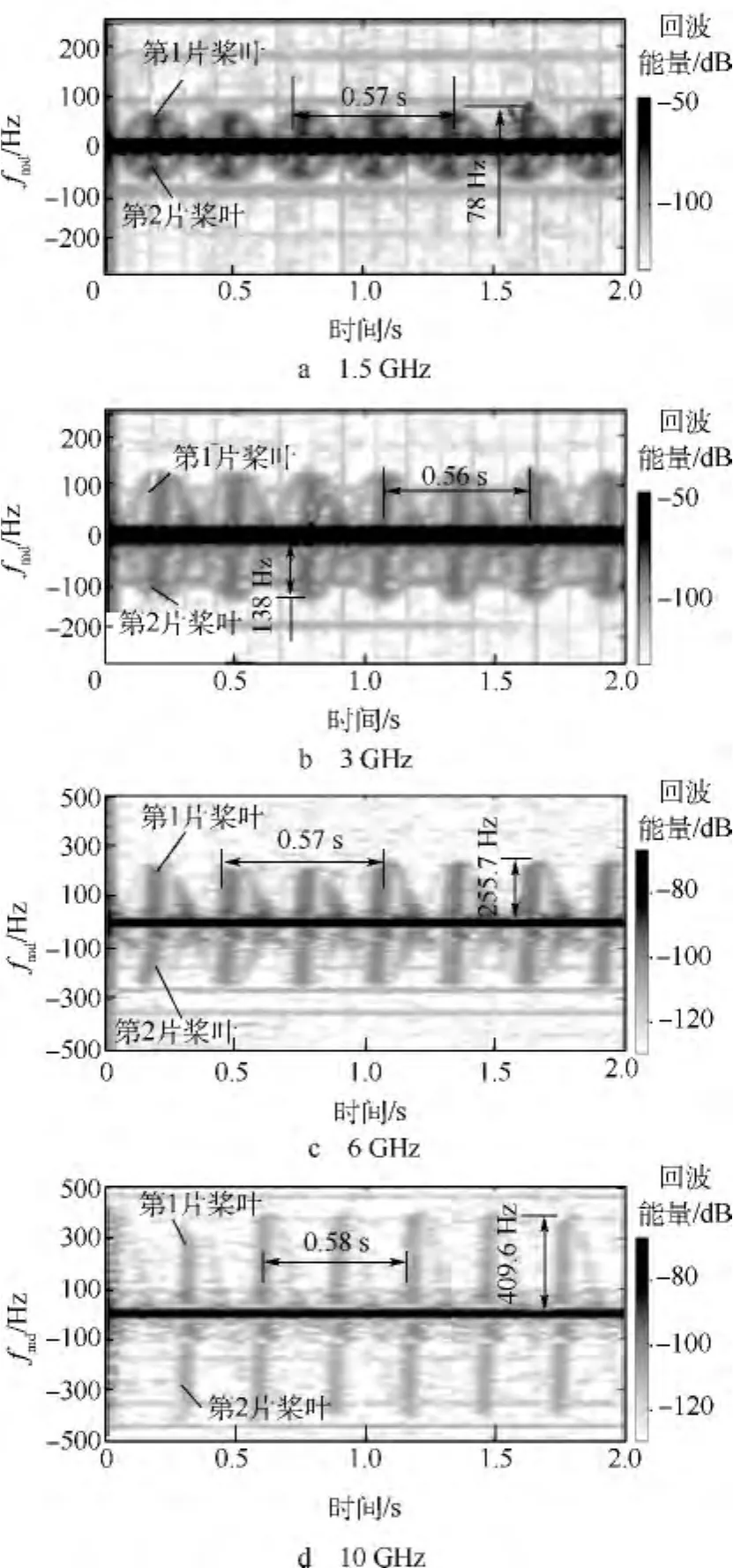
圖4 測試組號為3的參數設置

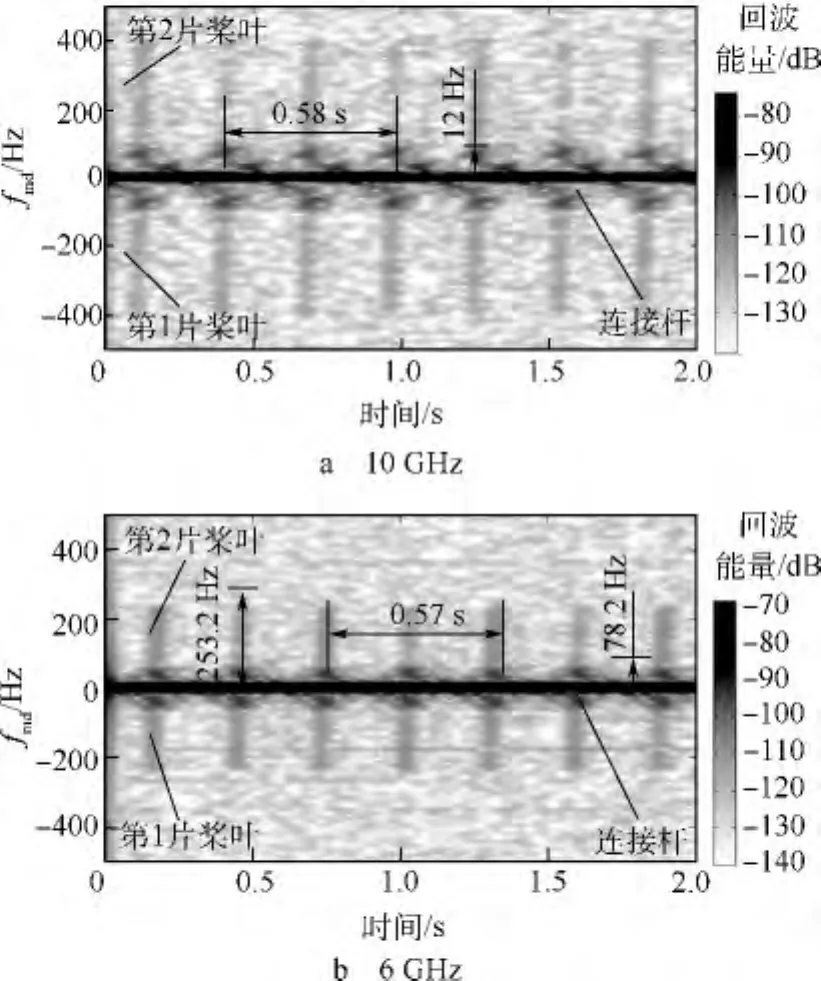
圖5 測試組號為4的參數設置

表4 估算出來的參數(槳葉b)

同時由表4和圖4可以看出，在水平極化時，測試頻率越低估算的旋翼尺寸越接近真實尺寸，如在1.5 GHz(3a)和3 GHz(3b)時估算旋翼尺寸分別為0.67，0.62 m，在實際值 0.65 m 左右，而在6 GHz(3c)和10 GHz(3d)附近估算的參數小于等于0.6 m，與實際值差異逐步變大.由圖4a～圖4d，低頻時，由于回波能量與目標在電場方向上投影尺寸相關性大，因此翼尖成像比較清晰，估算時比較清楚.高頻時，回波能量和目標形狀相關性較大，同時實驗模型的翼尖采用拋物線后掠形式，導致翼尖處的成像比較模糊，使估算尺寸相對變小.同時，由顏色深淺可以看出，低頻時，連接桿和電機槳轂差別比高頻時小，各部件成像分辨率低，不容易區分連接桿和旋翼;高頻時各部件分辨率高.

由圖4、圖5可以看出，水平和垂直極化相比時，槳葉和連接桿的對于極化敏感性不同，槳葉的細長體外形使得它對于極化敏感性比較強，所以使用垂直極化入射波能更好地估算出槳轂和連接桿的微多普勒特征參數，但對于槳葉的微多普勒特性估算能力則相對下降.

4 寬頻帶特性分析

對槳葉b進行微多普勒的寬帶特性研究，槳葉片數2片，槳葉轉速與上述相同，控制在1.75 r/s左右，測試頻率 4 ～8 GHz，中頻帶寬為1 kHz經過STFT處理后的時頻圖如圖6所示.

圖6 測試頻率為4～8 GHz的時頻圖

由圖6可以看出，由于頻寬已經對回波有相位調制作用，使得產生的微多普勒正負頻率不對稱，整體向負頻率方向平移，同時正負微多普勒頻率的斜率基本一致，為49.80附近.本次測試的斜率表征的是在周期為0.58 s，頻率為1 GHz產生的微多普勒頻移，由此可以估算出最小的旋翼半徑為0.66 m，與槳葉b的尺寸0.65 m基本一致，說明可以通過寬帶進行槳葉的半徑特性識別.

5 結論

針對兩種不同參數的旋翼槳葉，采用本文提出的實驗方法進行了深入研究，實驗結果表明，旋翼的微多普勒特性通過頻率把各個散射部件的回波能量分開，可用于指導旋翼的靜態RCS減縮設計.通過系列實驗測試，得到以下結果:①頻率特性，低頻時，翼尖成像清晰，到槳轂中心的距離估算較為精確，但對旋翼的部件特性識別不夠精確，即不容易分辨出槳葉和槳轂及連接桿的各自特征參數;高頻時，特性相反.②極化特性，槳轂、連接桿和槳葉的極化敏感性不同，垂直極化時可以很好地分辨槳轂和連接桿的微多普勒特征，但對槳葉的微多普勒特征估算能力下降.③寬頻帶特性，產生微多普勒特性向負頻率方向平移，但正負的微多普勒的斜率基本一致，同時可由斜率估算出旋翼的特征參數.

References)

[1]蒙志君，呂明云，武哲.動態槳葉RCS特性的實驗研究[J].北京航空航天大學學報，2006，32(9):1003－1006

Meng Zhijun，Lü Mingyun，Wu Zhe.Experimental investigation on RCS characteristics of rotating blades[J].Journal of Beijing University of Aeronautics and Astronautics，2006，32(9):1003－1006(in Chinese)

[2]Rotander C E，Von Sydow H.Classification of helicopters by the L/N-quoutient[C]//Radar System(RARDAR 97).Edinburgh，UK:IEE Publication，1997:629 －633

[3]Setlur P，Amin M，Thayaparan T.Micro-Doppler signal estimation for vibrating and rotating targets[C]//8th International Symposium on Signal Processing and its Applications，ISSPA 2005.Piscataway，NJ:IEEE，2005，2:639 －642

[4]Chen V C.Micro-Doppler effect in radar:phenomenon，model，and simulation study[J].Aerospace and Electronic Systems:IEEE Transactions on，2006，42(1):2 －21

[5]Chen V C.Analysis of radar micro-Doppler with time-frequency transform[C]//Statistical Signal and Array Processing.Pocono Manor，PA:IEEE，2000:463 －466

[6]Chen V C.Radar signatures of rotor blades[C]//Proceedings of SPIE on Radar Processing.Orlando，FL:SPIE，2001:63 －70

[7]Chen V C，Li F，Ho S S，et al.Analysis of micro-Doppler signatures[J].IEE Proceedings-Radar，Sonar and Navigation，2003，150(4):271－276

[8]陳行勇，黎湘，郭桂蓉，等.基于旋翼微動雷達特征的空中目標識別[J].系統工程與電子技術，2006，28(3):372－375

Chen Hangyong，Li Xiang，Guo Guirong，et al.Identification of air-target based on the micro-motion radar signatures of blades[J].Systems Engineering and Electronics，2006，28(3):372 －375(in Chinese)

[9]譚源泉，王厚軍，李良超，等.基于旋翼結構微多普勒特征的目標識別方法[J].電波科學學報，2013，28(1):50 －55

Tan Yuanquan，Wang Houjun，Li Liangchao，et al.Target identification method based on rotor structure micro-Doppler characteristics[J].Chinese Journal of Radio Science，2013，28(1):50 －55(in Chinese)

[10]Chen V C.The micro-Doppler effect in radar[M].Boston:Artech House，2011:110 －126

[11]Li P，Wang D C，Wang L.Separation of micro-Doppler signals based on time frequency filter and Viterbi algorithm[J].Signal，Image and Video Processing，2013，7(3):593 － 605

[12]Chen V C.Doppler signatures of radar backscattering from objects with micro-motions[J].IET Signal Processing，2008，2(3):301－311

[13]Chen V C，Lin C T，Pala W P.Time-varying Doppler analysis of electromagnetic backscattering from rotating objects[C]//The IEEE Radar.Piscataway，NJ:IEEE，2006:807 －812

[14]Thayaparan T，Abrol S，Riseborough E，et al.Analysis of radar micro-Doppler signatures from experimental helicopter and human data[J].IET Radar，Sonar ＆ Navigation，2007，1(4):289－299

[15]Chen V C，Ling H.Time-frequency transforms for radar imaging and signal analysis[M].Boston:Artech House，2002:25 －45