倒圓角直梁型柔性鉸鏈疲勞分析

肖圣龍

（廣東工業(yè)大學機電工程學院，廣東廣州 510006）

0 引言

柔性鉸鏈是柔順機構的重要組成部分。典型柔性鉸鏈在柔順機構中的應用最為廣泛，但也存在著運動空間較窄、強度較弱、適用范圍較小等問題，而復合型柔性鉸鏈不僅解決了上述問題，而且還具有較少的間隙、較高的定位精度和較好的疲勞性能。因此，復合型柔性鉸鏈在精密定位平臺中擁有極好的發(fā)展前景。

近年來，隨著計算機的高速發(fā)展，計算機仿真技術在產(chǎn)品研發(fā)過程中的運用越來越多，其中采用有限元仿真技術對產(chǎn)品機構進行疲勞分析更是一大趨勢。與傳統(tǒng)疲勞分析方法相比，有限元疲勞仿真技術能夠提供零部件表面的疲勞壽命分布，可以在產(chǎn)品的最初設計階段，通過確定零部件表面的疲勞壽命薄弱位置，可以極大的避免不良設計。

本文以一復合型柔性鉸鏈—倒圓角直梁型柔性鉸鏈為基體，通過有限元疲勞仿真實驗，得到倒圓角直梁型柔性鉸鏈表面的疲勞壽命分布，確定其薄弱位置的疲勞壽命，從而掌握了倒圓角直梁型柔性鉸鏈的使用壽命。

1 疲勞分析方法與過程

疲勞，是用來表述材料在循環(huán)載荷作用下的損傷和破壞。國際標準化組織對疲勞所做的定義是：“金屬材料在應力或應變的反復作用下所發(fā)生的性能變化叫做疲勞。”根據(jù)疲勞破壞發(fā)生時，材料的應力循環(huán)次數(shù)，疲勞破壞可以分為低周疲勞和高周疲勞兩種不同的破壞形式，對于不同的疲勞破壞形式，疲勞分析方法各不相同。工程設計中常用的疲勞分析方法有：名義應力法、局部應力應變、應力場強法和能量法。

雖然根據(jù)不同的適用范圍，疲勞分析方法不盡相同，但是疲勞分析方法都要通過以下步驟：（1）對零部件進行結構分析，確定零部件的危險部位；（2）進行材料的S-N疲勞實驗，得到材料的S-N曲線；（3）處理載荷，形成載荷譜；（4）選擇合適的疲勞損傷累積理論，得到零件危險部位的疲勞壽命。

設計人員將通過有限元分析得到的零部件表面的應力分布導入疲勞分析系統(tǒng)；然后在疲勞分析系統(tǒng)中選擇材料的S-N曲線，并輸入載荷譜；在確定合適的疲勞損傷累積規(guī)則后，疲勞分析系統(tǒng)便開始對零部件的危險部位進行疲勞分析，得到零部件危險部位的疲勞壽命，從而掌握整個柔性鉸鏈的疲勞壽命。傳統(tǒng)疲勞分析過程與有限元疲勞分析過程之間的比較如表1所示。

2 基于有限元倒圓角直梁型柔性鉸鏈疲勞分析

2.1 倒圓角直梁型柔性鉸鏈的數(shù)學模型建立

如圖1所示的倒圓角直梁型柔性鉸鏈，其缺口形狀由直梁型和直圓型復合而成。其桿部截面是矩形，鉸鏈由4個垂直于端面的1/4圓柱面和兩個矩形塊對稱切割而成。其結構參數(shù)為：寬度b、高度H、最小厚度t、倒圓角半徑R、直梁部分長度L。考慮到倒圓角直梁型柔性鉸鏈形狀較為復雜。因此，假定倒圓角直梁型柔性鉸鏈為一邊固定，另一邊上端受力。

2.2 倒圓角直梁型柔性鉸鏈的有限元分析

由于倒圓角直梁型柔性鉸鏈薄弱位置的極限載荷與運動范圍要求，選擇一組較為恰當?shù)臄?shù)據(jù)進行疲勞分析，選擇機構的幾何參數(shù)為b=0.2 mm，t=0.4 mm，R=0.8 mm，L=1.6 mm。

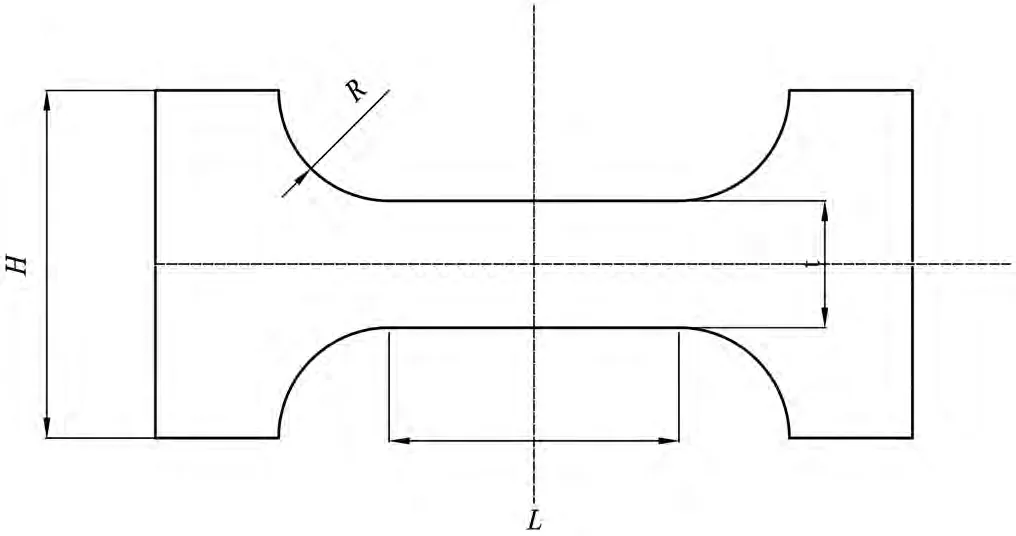
圖1 圓角直梁型柔性鉸鏈的結構圖

2.2.1 建立倒圓角直梁型柔性鉸鏈的有限元模型

有限元分析軟件可對倒圓角直梁型柔性鉸鏈的數(shù)學模型進行應力分析。如圖2所示，作者通過有限元軟件ANSYS建立了倒圓角直梁型柔性鉸鏈的有限元模型，單元數(shù)為8956，節(jié)點數(shù)為27559。

表1 傳統(tǒng)的疲勞分析與基于有限元疲勞分析之間的關系

圖2 倒圓角直梁型柔性鉸鏈的有限元分析

2.2.2 倒圓角直梁型柔性鉸鏈應力的有限元求解

根據(jù)倒圓角直梁型柔性鉸鏈的工作原理，對其添加了約束和外力（邊界條件為左邊固定，右邊上端施加力F），對倒圓角直梁型柔性鉸鏈的彎曲正應力進行數(shù)值求解。

倒圓角直梁型柔性鉸鏈承受100 N正壓力時的計算結果如圖3所示，可以看出最大彎曲正應力位于兩個缺口形狀的連接處。

由分析機構可知倒圓角直梁型柔性鉸鏈的最大彎曲應力小于材料的屈服極限。所以，倒圓角直梁型柔性鉸鏈產(chǎn)生疲勞破壞時，材料仍將處于彈性變形區(qū)。因此，采用名義應力法對倒圓角直梁型柔性鉸鏈進行疲勞分析，分析過程如下。

2.3 倒圓角直梁型柔性鉸鏈疲勞分析

將通過有限元分析得到的倒圓角直梁型柔性鉸鏈表面的應力分布導入疲勞分析系統(tǒng)，然后選擇材料的S-N曲線，并輸入載荷譜；最后，選擇合適的疲勞損傷累積理論，便可以開始對倒圓角直梁型柔性鉸鏈進行疲勞分析。

圖3 倒圓角直梁型柔性鉸鏈的彎曲應力分布圖

2.3.1 倒圓角直梁型柔性鉸鏈的工作情況

在倒圓角直梁型柔性鉸鏈工作過程中，最大應力小于材料的許用應力即可保證倒圓角直梁型柔性鉸鏈正常工作，因此分析倒圓角直梁型柔性鉸鏈應力的疲勞壽命時，只需對受到最大應力破壞的節(jié)點進行討論。利用靜力學進行疲勞分析，根據(jù)提供的材料參數(shù)，選擇材料的S-N曲線如圖4所示。

圖4 材料的S-N曲線

2.3.2 倒圓角直梁型柔性鉸鏈的載荷施加

倒圓角直梁型柔性鉸鏈在F=100 N的作用下做往復運動，其運動軌跡復符合正弦規(guī)律，輸入的載荷譜如圖5所示。

2.3.3 倒圓角直梁型柔性鉸鏈疲勞分析結果

根據(jù)倒圓角直梁型柔性鉸鏈載荷作用下的應力分布，計算其疲勞壽命，求得最大彎曲應力破壞的節(jié)點Node 1342在兩個缺口形狀的連接處，疲勞壽命為循環(huán)次數(shù)617 580次，在1×105～1×107范圍之內，屬于高周疲勞范疇。

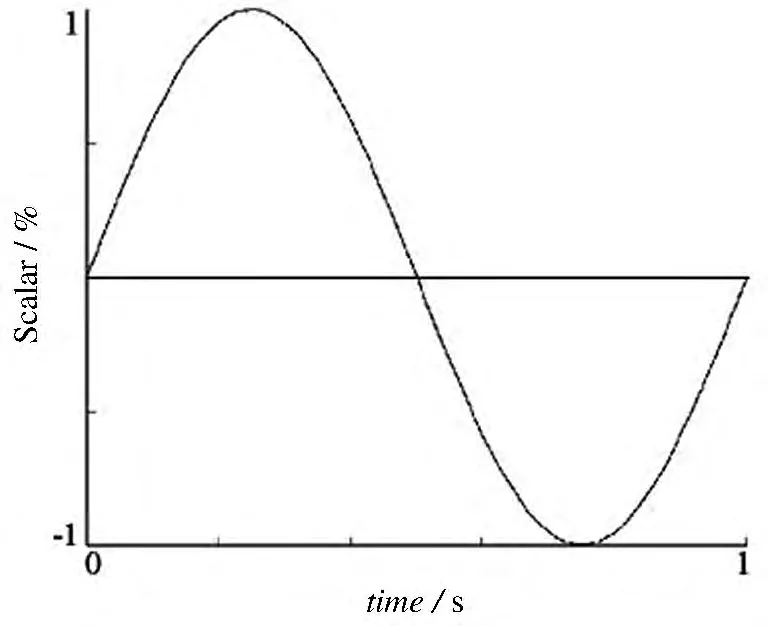
圖5 載荷譜

3 結論

本文通過對倒圓角直梁型柔性鉸鏈疲勞分析可知：

（1）有限元分析表明采用梁單元可準確模擬分析倒圓角直梁型柔性鉸鏈的內部應力；

（2）有限元仿真實驗結果表明：倒圓角直梁型柔性鉸鏈最大彎曲應力破壞點位于兩個缺口形狀的連接處，疲勞壽命循環(huán)次數(shù)為6.18×105次；

（3）倒圓角直梁復合型柔性鉸鏈的抗疲勞強度優(yōu)于直圓型柔性鉸鏈和直梁型柔性鉸鏈；

（4）研究的復合型柔性鉸鏈為倒圓角直梁型，對于雙曲線、橢圓、拋物線等其他曲線復合的柔性鉸鏈并沒有涉及，需要進行后續(xù)的研究。

［1］吳鷹飛，周兆英.柔性鉸鏈的設計計算［J］.工程力學，2002，19（6）：136-140.

［2］L.L.Howell.Compliant Mechanisms［M］.New York：John Wiley and Sons，2001.

［3］張志杰，袁怡寶.典型柔性鉸鏈柔度性能的計算與分析［J］.工程力學，2008，25（4）：106-110.

［4］劉慶玲，翁海珊，邱麗芳.新型單邊復和型柔性鉸鏈的柔度計算及其性能分析［J］.工程設計學報，2009，16（4）：276-280.

［5］姚衛(wèi)星.結構疲勞壽命分析［M］.北京：國防工業(yè)出版社，2003.

［6］Y.L.Lee，J.Pan，R.B.Hathaway，et al.Fatigue Test?ing and Analysis（Theory and Practice）［M］.USA：Elsevier Butterworth-Hernemann，2005.

［7］Y.Liu，S.Mahadevan.Multiaxial High-cycle Fatigue Criterion and Life Prediction for Metals［J］.Internation?al Journal of Fatigue，2005（27）：790-800.