吊車支撐力學計算模型建立及編輯程序處理研究
李 強
(大秦鐵路股份有限公司原平工務段,山西原平 034100)
0 引言
在國內外吊裝施工過程中,經常會發生因吊車支撐失穩而引發的吊車折臂、傾覆等重大安全事故,因此吊車支撐的力學狀態決定著吊車支撐的穩定性,是確保吊裝施工安全非常關鍵的力學參數。然而在實際吊裝施工作業過程中,現場工程技術管理人員存在著對吊車支撐力學計算理論不清楚、計算方法不科學的情況,本文就此問題進行了探討與研究,并引入了利用計算機高級語言編輯程序處理的計算理念,可以在確保計算精度的條件下最大程度的減少計算難度及工作量。
1 吊車支撐力學計算模型及計算難度
1.1 吊車支撐力學計算模型
吊車吊裝施工過程中,一般情況下是通過兩軸(①號軸~②號軸、③號軸~④號軸)、四支撐(1號,2號,3號,4號)的共同作用來保證吊車的穩定性。吊裝過程中的四支撐應力主要表現為豎向應力方向,吊車旋轉吊臂過程中,四支撐(1號,2號,3號,4號)通過豎向應力(T1,T2,T3,T4)的即時變化來平衡吊重彎矩M。
1.2 吊車支撐力學計算難度
吊車支撐力學計算的目標是求解四支撐的豎向應力值:T1,T2,T3,T4,而使用力學靜定平衡公式只能列出三個靜定方程,即:豎向應力平衡方程、X方向彎矩平衡方程、Y方向彎矩平衡方程。因此吊車支撐力學計算是一個空間超靜定問題,需使用工程力學中的“力法”“位移法”或其他工具(如:有限元分析法)等進行計算求解,這樣便導致理論計算難度高、計算工作量大,無法滿足在現場施工條件下使用及進行推廣。
2 吊車支撐力學計算模型的簡化分析
為了解決吊車支撐空間超靜定力學計算難題,在保證基礎理論分析正確及計算精度的前題下,對吊車支撐力學計算模型做了如下簡化與假定:
1)吊重彎矩M分拆。
使用向量分拆的方法將吊重彎矩M分拆為X方向Mx,Y方向My。
2)假定吊裝過程的兩個階段。
a.一階段:吊車重心位于四支撐幾何形心,吊車自重(含配重)及吊裝物的總重由四支撐共同承擔,即:原始單個支撐應力:
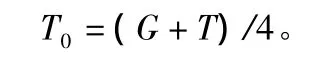
其中,G為吊車(含配重)的重量;T為吊裝物的重量。
b.二階段:由于Mx及My的作用引起吊車各支撐豎向應力ΔT1,ΔT2的變化(ΔT1,ΔT2可能為負值),即:吊裝過程中單個支撐應力為:TN=T0+ΔT1+ΔT2。
3)X方向假定。
將1號,3號支撐力T1,T3合并計為軸支撐力N1-3;將2號,4號支撐力T2,T4合并計為軸支撐力N2-4;由于Mx的作用軸支撐力N1-3減少ΔT1;由于Mx的作用軸支撐力N2-4增加ΔT1。
4)Y方向假定。
將4號,3號支撐力T4,T3合并計為軸支撐力N4-3;將2號,1號支撐力T2,T1合并計為軸支撐力N2-1;由于My的作用軸支撐力N4-3減少ΔT2;由于My的作用軸支撐力N2-1增加ΔT2。
5)使用力學靜定平衡公式分別對X方向、Y方向進行分析求解,以得出ΔT1,ΔT2值,最終求解吊裝過程中吊車各支撐應力TN。
3 吊車支撐力學計算公式的推導
根據吊車支撐力學計算的簡化模型,以吊臂旋轉作業范圍在Ⅰ象限區工作進行了分析,進而求解四支撐的豎向應力:T1,T2,T3,T4值。
3.1 X方向分析求解ΔT1
軸支撐力N1-3向吊車重心取力矩:
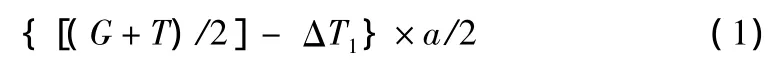
吊重彎矩M在X方向上的分量Mx:

軸支撐力N2-4向吊車重心取力矩:
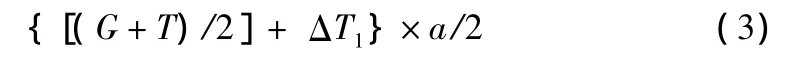
式(1)+式(2)=式(3)。
可得:ΔT1=T×L×sinθ/a。
3.2 Y方向分析求解ΔT2
軸支撐力N4-3向吊車重心取力矩:
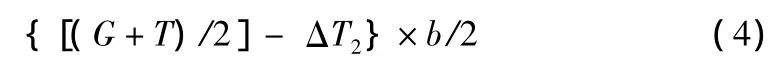
吊重彎矩M在Y方向上的分量My:

軸支撐力N2-1向吊車重心取力矩:
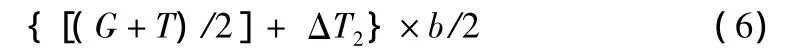
式(4)+式(5)=式(6)。
可得:ΔT2=T×L×cosθ/b。
3.3 求解吊車各支撐豎向應力 T1,T2,T3,T4 值
T1=[(G+T)/4]+[T×L×cosθ/(2×b)]- [T×L×sinθ/(2×a)]。
T2= [(G+T)/4]+[T×L×cosθ/(2×b)]+ [T×L×sinθ/(2×a)]。
T3= [(G+T)/4]-[T×L×cosθ/(2×b)]- [T×L×sinθ/(2×a)]。
T4= [(G+T)/4]-[T×L×cosθ/(2×b)]+[T×L×sinθ/(2×a)]。
其中,G為吊車(含配重)的重量;T為吊裝物的重量;a為吊車支撐一側寬度(平行于車縱向軸線);b為吊車支撐一側寬度(垂直于車縱向軸線);L為吊車臂最不利水平作業半徑;θ為吊車臂方向與Y軸夾角(平行于吊車車身方向)。
4 吊車支撐力學計算公式的分析
從推導出的吊車支撐力學計算公式中可以發現以下規律:
1)當吊車選型確定(即參數G,a,b確定),吊裝物重量確定(即參數T確定),吊車最不利水平作業半徑確定(即參數L確定),則吊車各支撐豎向應力由轉角θ確定,這便意味著吊車在吊重狀態下進行旋臂作業,吊車各支撐豎向應力處于即時的動態變化過程中。
在工程實踐時,需求解吊車應力最大支撐的最不利豎向應力值Tmax并結合地基承載力學參數,以便綜合采取科學有效的吊車支撐加固措施。
2)吊車支撐力學計算公式受轉角θ的影響,在Ⅱ象限區、Ⅲ象限區、Ⅳ象限區的表達形式與Ⅰ象限區略有不同,Ⅰ象限區四支撐中應力最大支撐為2號支撐。基于Ⅰ象限區計算公式經數學變換后可得出:Ⅱ象限區公式需將Ⅰ象限區計算公式轉角θ變換為-θ,四支撐應力最大支撐為1號支撐;Ⅲ象限區公式需將Ⅰ象限區計算公式轉角θ變換為π+θ,四支撐應力最大支撐為3號支撐;Ⅳ象限區公式需將Ⅰ象限區計算公式轉角θ變換為π-θ,四支撐應力最大支撐為4號支撐。
5 利用計算機V-foxpro語言編程解決吊車支撐力學計算問題
雖然已經推導出了各象限區吊車支撐力學計算公式,但是在求解吊車應力最大支撐的最不利豎向應力值Tmax過程中卻存在著重復計算,工作量大(頻繁的代入θ值進行試算)、計算數據對比繁瑣(需對比尋找數據拐點)等問題。而利用計算機高級語言編程計算則可以有效的解決此難題,使用計算機V-foxpro高級語言編程思想如下:
1)設計數據輸入模塊。
程序接收計算原始參數。如G為吊車(含配重)的重量;T為吊裝物的重量;a,b為吊車支撐兩側寬度;L為吊車臂最不利水平作業半徑。
2)設計各象限區吊車支撐力學計算模塊。
a.根據吊臂作業范圍選擇吊車工作象限區域。
b.設定初始轉角θ值(一般設置為0°);設計“累加計數器”及“累加計數器”精度(一般設置為1°);“累加計數器”計算機工作語言表達式為:θ=θ+1。
c.利用各象限吊車支撐力學計算公式,求解即時轉角θ值狀態下的吊車各支撐應力 TN值(T1,T2,T3,T4)。
d.利用V-foxpro高級語言“循環語句”,計算求解即時轉角θ+1值狀態下的吊車各支撐應力
3)設計計算數據邏輯對比模塊。
a.確定工作象限區域應力最大支撐TN作為對比目標:Ⅰ象限區應力最大支撐為2號支撐、Ⅱ象限區應力最大支撐為1號支撐;Ⅲ象限區應力最大支撐為3號支撐;Ⅳ象限區應力最大支撐為4號支撐。
c.綜合對比多個“計算拐點”,最大值則為最不利豎向應力值Tmax。
4)設計數據輸入模塊。
輸出各“計算拐點”值及最不利豎向應力值Tmax;輸出各“計算拐點”值及最不利豎向應力值Tmax對應的θ值。
5)根據最不利豎向應力值Tmax結合地基承載力學參數,對吊車各支撐采用針對性的預加固處理措施。如:增大支撐下受力面積;采用基礎換填的方法增加地基承載能力;采用樁基礎增加吊車支撐下承載能力等。
6 結語
采用理論計算的方法對吊車工作狀態下的支撐豎向應力進行安全評估并針對性的采取工程預加固措施,可以使現場施工擺脫傳統“施工經驗指導”的盲目性束縛;而采用計算機編輯程序處理的思想,可以使工程技術人員擺脫紛繁復雜的理論推導與工程計算。近幾年來,在我單位管轄范圍內進行的多處大型橋梁架設施工過程中都采用了此方法,收到了良好的安全效益與經濟效益。
[1]中華人民共和國鐵道部.鐵路工務安全規則[M].北京:中國鐵道出版社,2011.
[2]中華人民共和國鐵道部.鐵路技術管理規程[M].北京:中國鐵道出版社,2008.
[3]洪范文.結構力學[M].北京:高等教育出版社,2008.
[4]謝膺白.visual foxpro 9.0程序設計教程[M].西安:西安交通大學出版社,2007.

