高中數學自主探究學習模式研究
吳榮正
(蘇州工業園區星海實驗中學,江蘇蘇州,215021)
新課標的理念要求教學實踐的改革,教師教學方式也將隨著學生學習方式的改變而改變。教師只有在數學教學中不斷變換課堂教學方式,才能使課堂教學生動、形象,引起學生的興趣,使學生能夠自主選擇,運用自己喜歡的學習模式,在參與的過程中自主學習,使學生在教學過程中的主體地位真正得以體現。課堂采用多元化的教學方式,通過學生的參與、互動、體驗和實踐活動,使學生的語言綜合能力和自主學習能力得以不斷提高,樹立學習主人翁意識。
一、探究式教學的定義
探究式教學,又稱發現法教學,是指在學生學習一些概念和原理的過程中,打破傳統的教學方式,把原來教師直接講授改為在教師指導下學生通過觀察、閱讀、實驗、討論等方式自主學習,從而理解基本概念和原理,并達到一定效果的教學模式。
二、探究式教學的主體意識
學生是學習行為的主體,獲取知識是他們自我發展的起點,而內因是其獲取知識的關鍵所在。教師要善于激發學生學習的興趣,學生一旦有了興趣,其學習的過程將不再是一種額外的負擔。新課標的理念指引教師要從思想觀念上提升自己,要真正認識到學生才是學習的主人,要鼓勵每個學生,讓教師真正成為學生的學習伙伴。在探究式教學的過程中,教師要注意培養學生認真預習、專心聽課、及時復習、獨立完成作業、練后反思和觀察的習慣。
三、加強學生學習方法的指導
(一)學會閱讀
閱讀是自主學習的基礎。閱讀時,學生首先從書本或媒體感知文字或信息,然后用大腦進行分析與綜合、演繹與歸納等思維活動,并從中提取所需要的信息資料。教學實質上是教學生學會自主學習,而主動閱讀能力的培養正是探究式學習的基礎。
(二)學會思考
思考是學習的核心,閱讀后遇到問題就要思考,解決問題的過程本質就是獨立思考的過程。一個學生學習能力的高低在很大程度上取決于他的思維能力的高低。教師要通過教學的實踐活動,讓學生體驗數學知識的發現與探究過程,引領學生從特殊到一般,再從一般到特殊地認識事物,讓其體會具體問題具體分析的思維方式。
(三)學會調控
穩定而平和的心態對學習過程至關重要。學生在自主學習的過程中,有時會因成功而喜悅,有時也會因遇到困難和挫折而失落,這就需要他們能及時調整自己的心態,做到勝不驕敗不餒,避免狂妄與消沉,控制自己的情緒,不斷進取。要培養學生實事求是的態度,使之既能發現自身的長處又能看到自己的不足。只有能夠客觀地評價自己,才能制定目標,不斷調整心態,采取措施,控制行為,逐步成為品學兼優的學生。
四、優化培養學生自主學習能力的探究式教學模式
(一)問題推進式
教師不斷提出問題、學生不斷解決問題的過程是課堂教學的重要組成部分。精心設計課堂提問,對于指導學生逐步學會思考的方法、養成良好的習慣非常重要。問題推進式的教學結構是:設置情境—提出問題—解決問題—歸納總結。
附件一(探求課題《必修一》§2.1.1:函數的概念)
學習過程:
1.情境引入(實例引入)
思考問題一:請學生回顧初中學習過的函數的概念。
思考問題二:初中學習過哪些類型的函數?
思考問題三:y=1(x∈R)是函數嗎?
顯然,僅用上述函數概念很難回答這些問題,因此,需要從新的高度來認識函數概念。
2.講授新課
情景設置:在現實生活中,我們可能會遇到下列問題。
(1)估計人口數量變化趨勢是我們制定一系列相關政策的依據。從人口統計年鑒中可以查得我國從1949年至1999年人口數據資料(如表1所示),你能根據這個表說出我國人口的變化情況嗎?

表1 1949—1999年我國人口數據表
(2)一物體從靜止開始下落,下落的距離y(m)與下落時間x(s)之間近似地滿足關系式y=4.9x2。若一物體下落2 s,你能求出它下落的距離嗎?
(3)某市一天24小時的氣溫變化圖
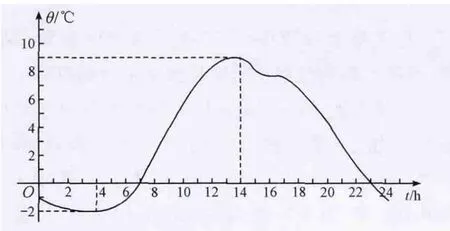
圖1 某市一天氣溫變化圖
①上午6時的氣溫約是多少?全天的最高、最低氣溫分別是多少?
②在什么時刻,氣溫為0℃?
③在什么時段內,氣溫在0℃以上?
思考問題五:如何用集合語言來闡述上述三個問題的共同特點?
3.函數概念的引入
思考問題六:根據以上共同特點,我們如何歸納出函數的定義?
(1)函數定義域:所有的輸入值x組成的集合;函數的值域:所有的輸出值y組成的集合。
(2)函數的構成要素:定義域、值域、對應法則。
思考問題七:函數定義域與函數定義中的非空數集A有什么關系嗎?
思考問題八:函數的值域與函數定義中的非空數集B有什么關系嗎?
思考問題九:函數的定義域可能為空集嗎?
(二)啟發討論式
這種教學模式,是以問題為核心,以學生自主學習為前提,通過教師與學生之間相互研討來實現教學目的的一種教學模式。這種教學模式創建了一個多向交流的平臺,為學生提供了一個可以發揮各自才能的空間,能最大限度地發揮學生在學習過程中的主體作用。啟發討論式教學模式,可以兼容其他教學方式。教師可以根據既定的教學目標,結合教學內容和教學條件,選擇適宜的討論方式。如以教師為主導的討論式:創設情境、提出問題—提供解決問題的思路、方法和材料—指導討論—歸納總結。這種方式較適合文科內容的教學,易于發揮求異思維,使學生成為學習的主人。
附件二(探求課題§2.1.1:函數的圖像)
探究任務:1.會畫函數圖像;2.了解研究函數圖像的意義。
學習過程:
思考問題一:請同學們回顧畫函數圖像的步驟?
學生探究活動:請同學們對初中學習的反比例函數及二次函數各舉一例(給定函數的定義域),再利用三角板、鉛筆畫出這兩個函數的圖像。
(選擇優秀的畫法展示,師生共同欣賞)
思考問題二:請你總結反比例函數及二次函數圖像作圖的經驗,并與同學們分享。
思考問題三:如果改變函數定義域,你覺得函數圖像會發生變化嗎?
思考問題四:設函數的定義域為A,則集合P={(x,y)|y=f(x),x∈A}與 Q={y|y=f(x),x∈A}相等嗎?請說明理由。
例題:試畫出函數f(x)=x2+1的圖像,并根據要求回答下列問題:
(1)比較 f(-2)、f(1)、f(3)的大小;
(2)若函數定義域為[-1,3],求函數的值域;
(3)若0<x1<x2,試比較 f(x1)與 f(x2)的大小,并說明理由;
(4)若 x1<x2<0,試比較 f(x1)與 f(x2)的大小,并說明理由;
(5)若|x1|< |x2|,試比較 f(x1)與 f(x2)的大小,并說明理由.
思考問題五:通過例題的成功解決,你覺得研究函數的圖像有什么意義?(可以幫助解決什么類型的問題)
(三)實踐探究式
這種教學模式強調將社會生活融入到教學中,可以把社會調查、實驗操作等作為提出問題并解決問題的途徑和手段。創造情境,提供條件與器材,讓學生動手實踐、親身體會,通過觀察測量等方式認識問題、提出問題,并通過分析研究等手段解決問題。
這種教學模式重在激發學習主體的學習興趣、并使其能夠拓展思維,主動認識事物、解決問題、自主學習。實質是“實踐—認識—再實踐—再認識”的過程,強調理論與實踐密切結合,為學生辯證思維的培養提供確切的方法。
附件三(研究性作業)
閱讀課本27頁,并利用Excel完成三個函數圖像的作圖,于本周六回家完成,作業以“班級—學生姓名—函數圖像”命名。
(1)f(x)=(x+1)2-1(-2≤x≤2)
(2)f(x)=x3(-5≤x≤5)
五、關于學生自主學習的管理策略
基于民主平等的師生關系,構建師生互動交流平臺,重視課堂上師生間情感的交流。教師授課時態度要親切,語言要富有感染力,要適時激發學生的求知欲,激勵學生勇于克服困難,使學生在積極緊張卻又輕松愉快的課堂氛圍中完成知識的學習及問題的探究。
探究式教學能夠在很多方面提升學生的能力,但是高中數學的知識面廣,知識的難度各有不同,如果全部采用探究式學習,很大程度上會影響教學的進度,也會對學生的學習興趣產生不利的影響。因此在高中數學探究式教學的過程中要精選內容,實施部分探究式與全部探究式相結合的方式。
[1]劉培杰.新編中學數學解題方法全書[M].哈爾濱:哈爾濱工業大學出版社,2007.
[2]華羅庚.科普著作選集[M].上海:上海教育出版社,1984.

